基于有向無環圖的區間覆蓋率求解算法

杜明　龐建成　周軍鋒

摘 要：給定一個有向無環圖，回答可達性查詢是圖的基本操作之一。雖然很多方法使用樹區間來加速可達查詢的處理速度，但并不明確使用多少個區間比較合適。本文提出一種快速計算區間覆蓋率的算法，該方法通過使用有效的剪枝策略來支持高效的覆蓋率計算。基于所得到的區間覆蓋率，可針對不同數據圖確定合適的區間個數，以便在加速查詢處理的同時，降低索引規模。基于多個真實數據集的實驗驗證了本文提出方法的高效性。

關鍵詞：有向無環圖;可達性查詢處理;區間覆蓋率

【Abstract】Givenadirectedacyclicgraph，answeringthereachabilityqueryisoneofthebasicoperationsofthegraph.Althoughmanymethodsusetreeintervalstospeeduptheprocessingspeedofreachablequeries，itisnotclearhowmanyintervalsareappropriate.Thispaperproposesanalgorithmtoquicklycalculatethecoverageofmultipleintervals.Thismethodsupportsefficientcoveragecalculationbyusinganeffectivepruningstrategy.Basedontheobtainedintervalcoverage，anappropriatenumberofintervalscanbedeterminedfordifferentdatagraphs，soastoreducetheindexscalewhilespeedingupqueryprocessing.Experimentsbasedonmultiplerealdatasetsverifytheefficiencyofthemethodproposedinthispaper.

【Keywords】directedacyclicgraph;reachabilityqueriesprocessing;intervalcoverage

作者簡介： 杜 明（1975-），男，博士，副教授，主要研究方向：自然語言處理、信息查詢、數據分析;龐建成（1995-），男，碩士研究生，主要研究方向：圖的可達查詢覆蓋率研究;周軍鋒（1977-），男，博士，教授，博士生導師，主要研究方向：大圖數據的查詢處理技術、推薦系統關鍵技術。

0 引 言

給定有向無環圖（DirectedAcyclicGraph，DAG），以及圖中任意兩個頂點u、v，可達性查詢u？→v用于回答從頂點u出發是否存在一條路徑可以到達頂點v。可達性查詢處理是圖數據管理與分析的基本操作之一，一直以來都是研究者廣泛關注的熱點問題[1-10]。在實際應用中，可達性查詢被廣泛應用到社交網絡、通信與傳感器網絡、生物網絡、可擴展標記語言數據、資源描述框架數據等領域，用于檢測兩點間是否存在特定關系。

雖然使用多個區間可以回答更多的可達性查詢，但是現在的方法并不明確使用多少個區間比較合適。一方面，使用多個區間可以擴大覆蓋率，從而增強區間標簽的剪枝能力;另一方面，使用多個區間也意味著較大的索引和較長的查詢響應時間。因此使用區間標簽來加速可達查詢處理時，一個關鍵問題是：應該建立多少個區間標簽，從而在查詢時間、索引大小以及索引構建時間之間獲得平衡。顯然，該問題的解決依賴于高效獲知區間標簽的覆蓋率，如此即可根據系統的硬件環境限制，選擇合適的區間個數，進而加速查詢響應的效率。

然而，覆蓋率的計算并非易事，原因在于不同生成樹區間所覆蓋的后代頂點有重復，多個區間覆蓋率并非簡單的累加和，需要在計算過程中去除重復部分。針對該問題，本文首次提出一種快速計算區間覆蓋率的算法，稱k-DFSIC（k-DepthFirstSearchIntervalCoverage），其中k表示生成樹區間的個數。該方法在求解覆蓋率時通過使用有效的剪枝策略來支持高效的覆蓋率計算，基于所得到的區間覆蓋率，用戶可針對不同數據圖確定合適的區間個數來獲得最佳的性能體驗。

本文的其余部分安排如下。第1節介紹相關工作，第2節提出求區間覆蓋率的算法，第3節展示實驗結果，第4節總結全文。

1 相關工作

1.1 問題定義

雖然可達性查詢針對的是一般有向圖，但是現有方法可以通過壓縮其中的強連通分量將其轉換為有向無環圖來處理，因此，本文假設輸入的都是有向無環圖。以下介紹區間覆蓋率的定義及問題的定義。

定義1 區間覆蓋率 給定有向無環圖及其生成樹上的多個區間，區間覆蓋率表示僅通過頂點的區間能回答的可達對個數占有向無環圖中所有可達對個數的比例。

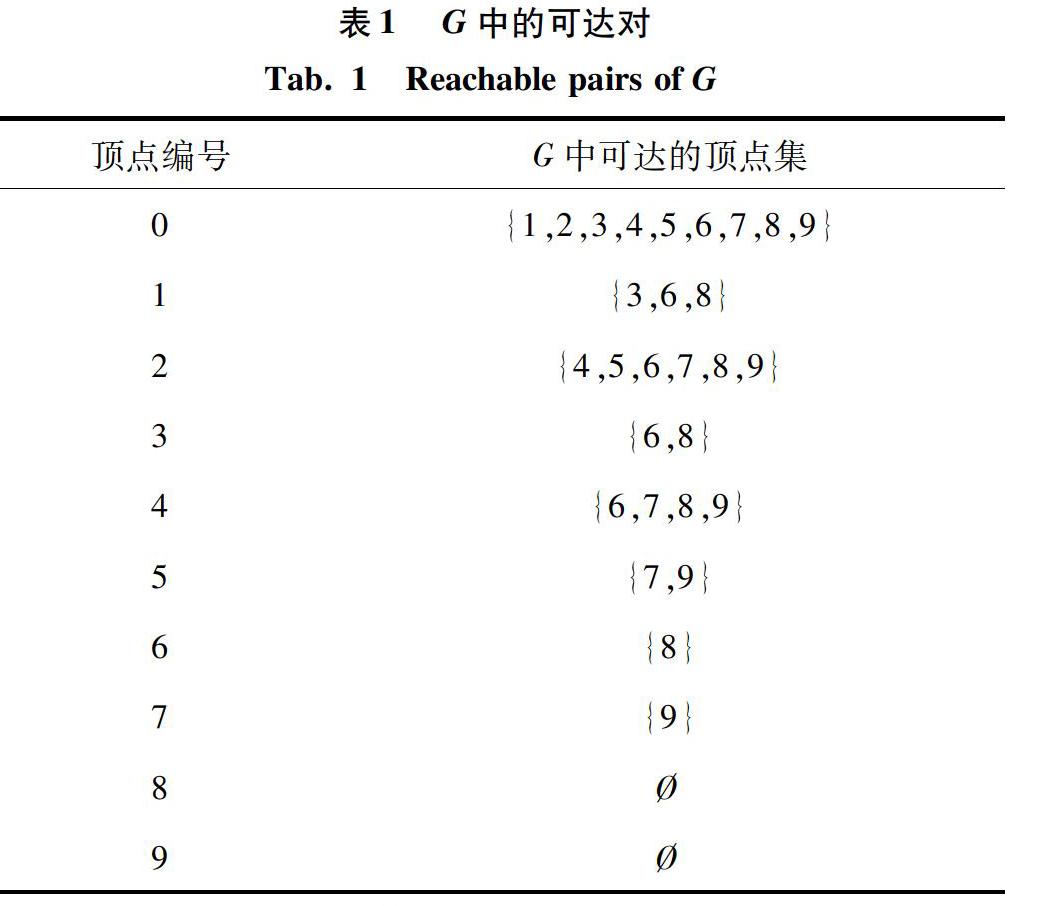
例如圖1（a）中有向無環圖G的所有可達對的數目為28，圖1（b）中所用一個生成樹區間能夠回答的可達對個數是22個，則使用一個區間時，其區間覆蓋率為22/28，圖1（c）中使用2個生成樹區間能夠回答的可達對個數是26個，則其區間覆蓋率為26/28。

問題定義： 給定有向無環圖及其對應的多個生成樹區間，返回這些生成樹的區間覆蓋率。

1.2 相關算法

雖然區間覆蓋率可用于協助用戶針對不同圖來確定合適的區間個數，但關于區間覆蓋率的計算問題還未見到任何研究，本文首次對區間覆蓋率的問題進行研究，提出一種快速計算區間覆蓋率的算法。這里，研究中僅討論使用區間的可達性查詢處理算法，包括GRAIL[11]、FERRARI[5]、FELINE[12]三個算法。對此可做闡釋分述如下。

GRAIL算法基于生成樹為每個點附加多個區間，其中一半區間是包含所有圖中后代的區間，用于判斷不可達，另外一半區間是包含生成樹中后代的區間，用于判斷可達。由于區間個數會影響索引大小及查詢效率，本次研究在進行實驗時，基于數據圖的稀疏程度來設定區間個數。對于稀疏圖（度小于2），使用2個區間，其它圖使用5個區間。該方法是一種基于經驗的直覺，區間增多時，不一定能增強查詢處理能力。

FELINE用x和y表示頂點的2個拓撲號，用I表示頂點的區間標記。在判斷頂點u是否可達頂點v的時候，如果頂點的拓撲號滿足xu>xv或者yu>yv，則可知頂點u不可達頂點v;如果xu

FERRARI根據內存的限制情況來確定區間個數，由于區間之間有重疊，因此即使內存夠大，可支持多個區間，但卻仍然難以保證查詢效率。

以上方法雖然都使用區間來加快可達性查詢的處理效率，但是這些方法都不能確定應該使用多少區間來回答才合適，針對該問題，本文提出一種快速計算區間覆蓋率的方法，以便針對不同數據圖確定合適的區間個數，從而提升查詢效率并減小索引規模。

2 求區間覆蓋率的算法

2.1 基礎算法

給定有向無環圖G及其生成樹上的k個區間，求區間覆蓋率的基本思想是：首先找到圖G中所有的可達對;然后判斷這些可達對是否能通過區間回答，能回答說明該可達對能夠通過區間判斷，不能回答則說明該可達對不能通過區間判斷;最后求出可以通過區間回答的可達對個數占圖G中所有可達對個數的比例，即可得到使用k個生成樹區間的覆蓋率。

算法1展示了基礎算法求區間覆蓋率的偽代碼，具體如下。

算法中，第1行設置2個變量nRch和nUnRch，分別表示可以通過生成樹區間回答的可達對個數和不能通過生成樹區間回答的可達對個數，并將其初始值設為0;第2～7行針對圖G中所有的可達對，依次判斷其是否能通過給定的k個區間回答，如果可以回答，nRch++，如果不能回答，則nUnRch++;第8行通過nRch的值除以（nRch+nUnRch）的值求出使用k個生成樹區間的覆蓋率。

給定有向無環圖G見圖1（a）。首先找到圖G中所有的可達對，詳見表1，總共有28個;然后判斷這些可達對能否通過給定的區間回答。研究可知，圖1（b）為圖G中每個節點給定了一個生成樹區間，[8，9]（v7的區間）[7，9]（v4的區間），說明v4→v7可以通過該區間回答，則通過一個區間能回答的可達對個數nRch++，而[4，5]（v6的區間）[7，9]（v4的區間），說明v4→v6不能通過該區間回答，則不能通過一個區間回答的可達對個數nUnRch++，當圖G中所有可達對判斷結束后，可以得到nRch為22，nUnRch為6，故通過計算可得使用一個區間的覆蓋率是22/（22+6），即22/28。研究中的圖1（c）又為G中每個節點給定了2個生成樹區間，[5，5]（v6的第二個區間）[3，7]（v4的第二個區間），說明v4→v6可以通過該區間回答，則通過2個區間能回答的可達對個數nRch++，而[6，7]（v7的第二個區間）[8，8]（v5的第二個區間），說明v5→v7不能通過該區間回答，則通過2個區間不能回答的可達對個數nUnRch++;當圖G中所有可達對判斷結束之后，可得nRch為26，nUnRch為2，則通過計算可得使用2個區間的覆蓋率是26/（26+2），即26/28。

基礎算法若要枚舉有向無環圖G中所有的可達對，需要的時間為O（kn（n+m）），其中n為G的頂點個數，m為G的邊數。判斷每個可達對能否通過生成樹區間回答，可以在O（k）時間內完成，故基礎算法的時間復雜度是O（kn（n+m））。

2.2 k-DFSIC算法

由于基礎算法在計算過程中需要枚舉有向無環圖中所有的可達對，時間復雜度太大，在實踐中無法處理大圖。針對該問題，本文提出一種快速計算區間覆蓋率的k-DFSIC算法。給定有向無環圖G及其k個生成樹區間，求區間覆蓋率之前，為圖中每個節點設定一個計數器，表示該節點通過區間能回答的可達對個數，初始值為第一個區間的長度。求區間覆蓋率的基本思想是：當求解頂點u的第i個區間新增的可達查詢數量時，對于第i個區間中的所有生成樹后代點，即檢視u與其之間的可達性是否可以通過前i-1個區間來判斷。如果可以，則u的計數器不變，否則說明該可達對無法通過前i-1個區間判斷，則u的計數器加1。當所有頂點處理結束后，將頂點的計數器累加，即可得到所有節點通過區間能回答的可達對個數。該值除以圖G中所有可達對個數，就是使用k個區間的覆蓋率。

算法2展示了k-DFSIC算法求區間覆蓋率的偽代碼，具體如下。

算法中，第1行設置了一個變量nTC表示有向無環圖G的傳遞閉包的大小;第2行設置了一個變量nRCH表示圖G中所有節點通過區間能回答的可達對個數，并設其初始值為0;第3行為圖G中每個節點u給定一個計數器表示該節點通過區間能回答的可達對個數nRch，其初始值為節點u的第一個區間長度;第4～12行在求解節點u通過i（2≤i≤k）個區間新增的可達查詢數量時，對于第i個區間中的所有生成樹上后代節點v，設置一個變量flag表示u和v之間的可達性是否可以通過前i-1個區間來判斷，其初始值設為TRUE，如果u和v之間的可達性可以通過前i-1個區間來判斷，則flag值為FALSE，判斷后如果flag值為TRUE，說明該可達對無法通過前i-1個區間判斷，則nRch加1;第13～14行將圖G中每個節點的計數器nRch加和即所有節點通過區間能回答的可達對個數nRCH，用nRCH的值除以圖G中所有可達對的個數nTC，即可得到使用k個區間的覆蓋率。

例如，圖1（a）所示有向無環圖G中所有可達對共有28個，參見表1，即圖G的傳遞閉包的大小nTC為28。

由圖1（b）可知，為圖G中每個節點給定了一個區間，并為每個節點給定一個計數器表示該節點通過一個區間能回答的可達對個數nRch為該節點的區間長度，比如說v4的區間是[7，9]，則v4通過一個區間能回答的可達對個數nRch為v4的區間長度2，將每個節點的nRch值加和可以得到所有節點通過一個區間能回答的可達對個數nRCH為22，則使用一個區間的覆蓋率是22/28。

由圖1（c）可知，為圖G中每個節點給定了2個區間，并為每個節點給定一個計數器表示該節點通過2個區間能回答的可達對個數nRch首先設置為該節點的第一個區間的長度，對于生成樹上每個節點來說，要找到該節點到其后代節點的所有可達查詢，參見表2，并檢查這些查詢能否通過前i-1個區間回答來更新nRch的值，比如v4節點，v4的第一個區間是[7，9]，則v4通過2個區間能回答的可達對個數nRch首先設置為v4的第一個區間的長度2，然后依次檢查v4→v6，v4→v7，v4→v8，v4→v9能否通過前i-1個區間回答來更新nRch的值，可以發現v4→v6不可以通過第一個區間回答，但是可以通過第二個區間回答，則nRch++，同理v4→v8也不可以通過第一個區間回答，但是可以通過第二個區間回答，則nRch++，而v4→v7，v4→v9已經可以通過第一個區間回答了，則nRch值不變，當所有查詢判斷結束之后，可以得到v4通過2個區間能回答的可達對個數nRch為4;將每個節點的nRch值加和可以得到所有節點通過2個區間能回答的可達對個數nRCH為26，則使用2個區間的覆蓋率是26/28。

k-DFSIC算法需要在有向無環圖G上找到其生成樹上的每個節點的后代節點。和基礎算法不同，基礎算法需要枚舉圖上的后代，而k-DFSIC只需要枚舉樹上的后代，該值等于樹上每個頂點的高度之和。假設頂點的平均高度是h，則求解可達對個數nRCH的代價是O（k（n+m）+khn），其中n為G的頂點個數，m為G的邊數;同時，求傳遞閉包的時間代價為O（wm）[13]，這里w是求傳遞閉包大小過程中，處理每個點時平均處理代價。因此，k-DFSIC的時間復雜度是O（k（n+m）+khn+wm）。

3 實驗分析

3.1 實驗環境

實驗所用的硬件平臺是IntelCorei5-4460主頻為3.20GHz的CPU，4GB的RAM內存，操作系統為Ubuntu8.3.0，并使用gcc8.3.0進行編譯，以上算法均采用C++語言實現。

3.2 數據集

本文中使用的12個數據集見表3。這些數據集都廣泛地出現在圖的可達查詢研究中[4-5，9，14-16]，這些數據集都是有向無環圖，表3中標注了每個數據集的頂點數|V|以及邊數|E|。

3.3 索引大小

k-DFSIC算法求區間覆蓋率使用不同區間時的索引大小見表4。由表4可以看出隨著區間個數的增加，索引大小呈線性增加。

3.4 覆蓋率求解時間

表5比較了基礎算法和k-DFSIC算法求區間覆蓋率所需的時間。由表5可以發現k-DFSIC算法與基礎算法相比，在使用相同區間個數的情況下，所需的時間要少得多，并且基礎算法在大圖當中運行時間太長，而k-DFSIC算法則只需很少的時間，表5中，“-”表示基礎算法運行時間超過了2h。

3.5 區間覆蓋率

表6展示了本文實驗所得到的區間覆蓋率。由表6發現隨著區間個數的不斷增加，覆蓋率雖然也不斷增加，但是有的數據集覆蓋率增加值比較小，比如twitter數據集;而有的數據集覆蓋率增加值比較大，比如xmark數據集，使用5個區間時的覆蓋率是使用1個區間時覆蓋率的3倍多。

3.6 實驗結論

首先，本文提出的區間覆蓋率計算算法可高效求解區間覆蓋率，在實際中需要了解區間覆蓋率的情況下，可通過使用本文提出的算法進行高效求解;其次，通過本文實驗所得到的區間覆蓋率，可以發現有些數據集只需要使用2個區間來回答可達性查詢就比較合適了，比如human數據集，而有的數據集使用5個區間比較合適，比如xmark數據集。假設內存足夠的情況下，考慮到查詢效率，針對不同數據集回答可達性查詢合適的區間個數見表7;如果內存不足以使用多個區間，則需要用戶根據實際情況確定合適的區間個數。

4 結束語

本文針對已有算法回答可達性查詢時使用樹區間來加快處理速度、但是并不明確使用多少個區間比較合適的問題，首次提出了一種快速計算區間覆蓋率的算法。實驗結果表明，本文提出的算法可高效計算區間覆蓋率。基于所得到的區間覆蓋率，用戶可結合實際應用環境的限制確定可達查詢處理過程中應該使用的區間數量，從而獲得最佳的性能體驗。

參考文獻

[1] AGRAWALR，BORGIDAA，JAGADISHHV，etal.Efficientmanagementoftransitiverelationshipsinlargedataandknowledgebases[J].ACMSIGMODRecord，1989，18（2）：253-262.

[2]CHENGJ，HUANGS，WUH，etal.TF-Label：Atopological-foldinglabelingschemeforreachabilityqueryinginalargegraph[C]//Proceedingsofthe2013ACMSIGMODInternationalConferenceonManagementofData.NewYork，USA：ACM，2013：193-204.

[3] JINR，WANGG.Simple，fast，andscalablereachabilityOracle[J].VeryLargeDataBases，2014，6（14）：1978-1989.

[4]JINRuoming，XIANGYang，RUANNing，etal.Efficientlyansweringreachabilityqueriesonverylargedirectedgraphs[C]//Proceedingsofthe2013ACMSIGMODInternationalConferenceonManagementofData.Vancouver，BC，Canada：ACM，2008：595-608.

[5]YILDIRIMH，CHAOJIV，ZAKIMJ.GRAIL：Ascalableindexforreachabilityqueriesinverylargegraphs[J].TheVLDBJournal，2012，21（4）：509-534.

[6]ZHANGTianming，GAOYunjun，LICongzheng，etal.Distributedreachabilityqueriesonmassivegraphs[M]//LIG，YANGJ，GAMAJ，etal.DatabaseSystemsforAdvancedApplications.DASFAA2019.LectureNotesinComputerScience.Cham：Springer，2019，11448：406-410.

[7]SENGUPTAN，BAGCHIA，RAMANATHM，etal.ARROW：ApproximatingreachabilityusingrandomwalksoverWeb-scalegraphs[C]//InternationalConferenceonDataEngineering.Macao，China：dblp，2019：470-481.

[8]BENDERMA，FINEMANJT，GILBERTS，etal.Anewapproachtoincrementaltopologicalordering[C]//SymposiumonDiscreteAlgorithms.Austin，Texas：dblp，2009：1108-1115.

[9]JAGADISHHV.Acompressiontechniquetomaterializetransitiveclosure[J].ACMTransactionsonDatabaseSystems，1990，15（4）：558-598.

[10] CHENY，CHENY.AnEfficientalgorithmforansweringgraphreachabilityqueries[C]//IEEE24thInternationalConferenceonDataEngineering.Paris，France：IEEE，2008：893-902.

[11] YILDIRIMH，CHAOJIV，ZAKIMJ.Grail：Scalablereachabilityindexforlargegraphs[J].ProceedingsoftheVLDBEndowment，2010，3（12）：276-284.

[12] VELOSORR，CERFL，JrMEIRAW，etal.Reachabilityqueriesinverylargegraphs：Afastrefinedonlinesearchapproach[C]//17thInternationalConferenceonExtendingDatabaseTechnology.Athens，Greece：dblp，2014：511-522.

[13] TANGXian，CHENZiyang，LIKai，etal.Efficientcomputationofthetransitiveclosuresize[J].Clust.Comput.，2019，22（Supplement）：6517-6527.

[14] JINR，RUANR，DEYS，etal.SCARAB：Scalingreachabilitycomputationonlargegraphs[C]//Proceedingsofthe2012ACMSIGMODInternationalConferenceonManagementofData.Scottsdale：ACM，2012：169-180.

[15] CHAM，HADDADIH，BENEVENUTOF，etal.MeasuringuserinfluenceinTwitter：Themillionfollowerfallacy[C]//ProceedingsoftheFourthInternationalConferenceonWeblogsandSocialMedia（ICWSM2010）.Washington，DC，USA：dblp，2010：10-17.

[16] VanSCHAIKSJ，DeMOORO.Amemoryefficientreachabilitydatastructurethroughbitvectorcompression[C]//Proceedingsofthe2011ACMSIGMODInternationalConferenceonManagementofData.Athens，Greece：ACM，2011：913-924.