基于PVS算法的六子棋博弈系統(tǒng)的研究
王鴻菲 王靜文 李媛


摘要:針對六子棋比賽中基于棋型分析的評估函數(shù)比較復雜,因此搜索效率大大降低,六子棋是一種復雜度與象棋相當?shù)牟┺挠螒颉F鋸碗s性主要是平均分枝因子大,導致博弈樹搜索的深度太淺。本文采用了PVS搜索算法,通過縮小搜索范圍,從而有效增加剪枝效率,同時結(jié)合了迭代深化和歷史啟發(fā)增強及置換表和哈希表技術(shù),極大提高了搜索效率和深度。使用該技術(shù)開發(fā)的六子棋系統(tǒng),其博弈水平得到了有效提高。
關(guān)鍵詞:六子棋;PVS;路;歷史啟發(fā)增強;迭代加深;置換表
【Abstract】TheevaluationfunctionbasedonchesstypeanalysisiscomplexinthegameofConnect6,sothesearchefficiencyisgreatlyreduced.Thecomplexityismainlyduetothelargeaveragebranchingfactor,whichleadstotheshallowdepthofgametreesearch.Inthispaper,PVSsearchalgorithmisusedtoreducethesearchscope,soastoeffectivelyincreasethepruningefficiency.Atthesametime,thecombinationofiterativedeepening,historicalheuristicenhancement,replacementtableandHashtabletechnologygreatlyimprovethesearchefficiencyanddepth.ThegamelevelofConnect6systemdevelopedbythistechnologyhasbeeneffectivelyimproved.
【Keywords】Connect6;PVS;road;historicalheuristicenhancement;iterativedeepening;Hash
作者簡介:王鴻菲(1999-),男,本科生,主要研究方向:計算機博弈;王靜文(1965-),男,工程師,主要研究方向:人工智能和信息安全;李媛(1976-),女,博士后,教授,主要研究方向:人工智能和隨機過程。
0引言
機器博弈是人工智能研究中極具挑戰(zhàn)性的重要課題之一,其技術(shù)進步則為人工智能領(lǐng)域的研究融匯了為數(shù)可觀的理論和方法,對社會及學術(shù)方面產(chǎn)生了廣泛而深遠的影響。機器博弈并不是如人們設(shè)想的那樣只是人和計算機間簡單的下棋小游戲,而是通過這種競爭性的活動來檢驗人工智能成果是否達到了人的智能水平。在社會的日常生活中經(jīng)常面臨著決策問題,而建立和選擇決策的過程便是計算機博弈研究關(guān)注的內(nèi)容,所以在智能決策、沙盤推演等場景中均有著現(xiàn)實應用意義。
由于六子棋的棋盤與圍棋棋盤相同[1],并有與圍棋有著相同的狀態(tài)空間復雜度,吸引了越來越多的計算機博弈愛好者對六子棋的關(guān)注。本文擬對此展開研究論述如下。
1六子棋簡介
六子棋是近些年新興起的棋類博弈項目,是國立交通大學吳毅成教授提出的“連K”系列棋之一[2]。對其特點可概述為:
(1)規(guī)則簡單,六子棋有黑白兩方,黑方先落子。黑方第一步下一顆子,隨后黑白雙方輪流落兩子。連成六子或以上獲勝。沒有禁手,長連即連成六子以上也為贏,如果棋盤被下滿時仍未分出勝負則算和棋,若不同意和棋,也可按照存在五連的數(shù)量來定勝負,減少和棋局面的出現(xiàn)。六子棋的標準棋盤如圖1所示。
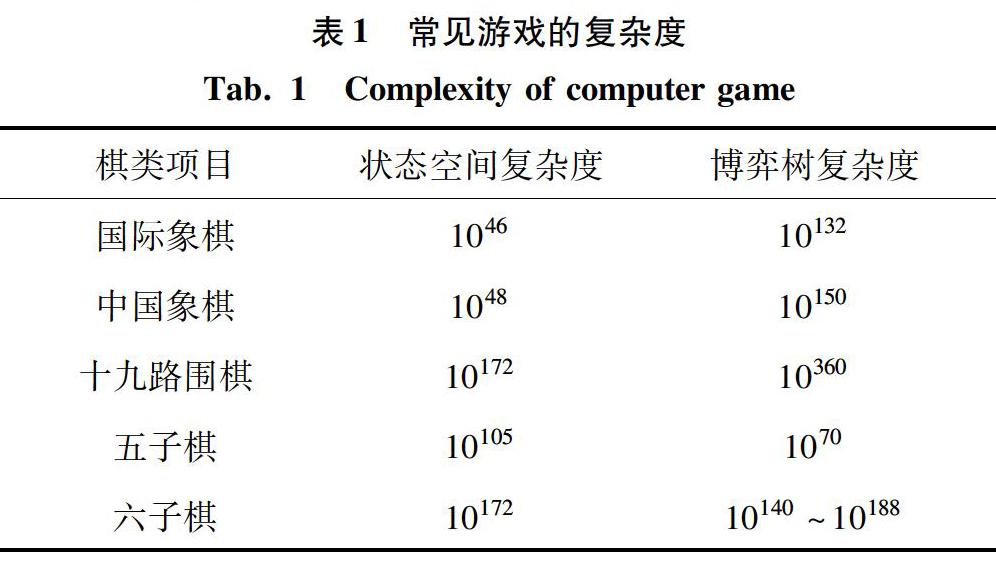
(2)變化復雜。對于機器博弈來說,一般采用狀態(tài)空間復雜度和博弈樹復雜度來衡量某種博弈游戲的復雜程度。狀態(tài)空間復雜度,指的是從游戲最開始的狀態(tài)可以變化出的符合規(guī)則的狀態(tài)的數(shù)量[3]。在六子棋的對弈過程中的每一個局面都對應一個節(jié)點,而一個節(jié)點下面又有很多子節(jié)點,所以不斷地向下推演就可以建立整個博弈樹,直至得到博弈結(jié)果。但得到的博弈樹是巨大的,隨著不斷地加深,子節(jié)點將以幾何方式上升。常見棋類的復雜度對比見表1。
從表1中可以看到,六子棋比五子棋的復雜度高[4-5],和象棋差不多或略高一點。
(3)游戲公平。由于各方每次下完一手后,盤面都比對方多一子,因此賽局自然達成平衡的狀態(tài),這大大提升了六子棋的公平性。不像許多棋種、如五子棋、象棋、國際象棋,先下者會占據(jù)一些優(yōu)勢。
2六子棋博弈系統(tǒng)
計算機博弈游戲的核心由搜索和估值兩部分組成。其中,估值是用于準確地評價當前局面,而搜索則是根據(jù)當前局面獲得最佳下法。這里將給出探討分述如下。
2.1估值函數(shù)
在博弈比賽的對弈中,如果將棋局的所有狀態(tài)都列舉出來,就一定可找到最佳的走法,但是對于博弈來說,這種做法不僅是無意義的,對于大部分棋種也是不可行的。因此對博弈樹的窮舉搜索必須適可而止,由此可知研究中搜索的深度是有限的,即可根據(jù)在一定深度處的節(jié)點的估計值來評分,就是估計值代替實際的搜索,這就叫做估值函數(shù)。不管對黑方、還是白方,都是利于對博弈樹進行捜索找到最佳走法的。如果不能窮舉所有走法,就只能在搜索到一定層后,根據(jù)對局面的估值來判斷路徑的好壞,此時就要設(shè)計出評估函數(shù)來對局面進行估值。估值方法往往和具體的棋類規(guī)則結(jié)合緊密,這在很大程度上決定了博弈程序的棋力高低[6]。研究時,既可以向估值函數(shù)寫入棋類知識,使程序?qū)τ诰置娴脑u估更為精確,也可以寫出簡化的估值函數(shù),使估值的過程簡捷、且節(jié)省運算時間,期望通過更深的搜索提高棋力。
目前,六子棋普遍采用2種估值方式。一種是基于“路”的方式進行估值,另一種就是基于“棋型”的方式進行估值。這里,基于“路”或基于“棋型”,則是指根據(jù)路或棋型的方式對棋盤進行掃描。
需要指出的是,在基于棋型的估值中,由于目前常見的10種棋型都是通過經(jīng)驗總結(jié)的,主觀因素影響較大,可能存在未定義的其他棋型。同時因為同一種棋型也有多種可下位置。
所以棋形判斷的復雜度高,計算量大,受計算機博弈比賽中六子棋博弈時間的約束,搜索的深度和寬度都會受到限制。故而本文提出基于路的估值方法,相對于基于棋型的估值較為簡單,實現(xiàn)上較為容易,搜索時間也較短,更適合在在博弈比賽中付諸應用。
基于路的估值,在一個棋盤中,將路分為6種,掃描連續(xù)的同一條直線上的6個不同的位置,再對同一個顏色的棋子進行計數(shù),從而判斷為幾路。因此可以計算出一個棋盤有:水平方向為19×14=266;豎直方向為19×14=266;
左斜方向14×14=196;右斜方向14×14=196,所以一共有294路。本文采用了4個方向的函數(shù)實現(xiàn)路的掃描。研究后推得AnalysisRight主要偽碼可表示如下:
IntAnalysisRight(charposition[19],inti,intj){
chartempArray[19];
intx;
inty;
intrealnum;
if(18-j y=18; x=j-18+i; } else{ x=0; y=i+j; } intg=0; for(intk=0;k<19;k++){ if(x+k>18||y-k<0){ break; } tempArray[k]=position[x+k][y-k]; g++; } AnalysisLine(tempArray,g,y-j); for(ints=0;s if(m_LineRecord[s]!=WEIFANGWEN){ TypeRecord[x+s][y-s][3]= m_LineRecord[s]; } } returnTypeRecord[i][j][3]; } 其它各個方向上的計算方法和上述偽碼的計算方法相同。文中不再做過多贅述。 2.2基于PVS的搜索算法 六子棋的復雜度高,一般的搜索算法難以達到較高的搜索效率。目前,常用的方法有alpha-beta算法、UCTS算法等[7]。其中,alpha-beta算法在經(jīng)過剪枝處理后,卻仍然還是存在大量的節(jié)點需要去遍歷,搜索效率較低;UCTS算法可以達到較好的搜索深度,但得到的估值準確性較低。 本文的搜索算法是基于PVS算法。PVS算法,也稱最小窗口搜索算法,是由alpha-beta變形而來。兩者間的主要區(qū)別就在于:除了主變量外的其它節(jié)點都進行零窗口搜索,并且把α的值復制為β的值,通常情況下都是把每個節(jié)點的所有子節(jié)點進行排序,同時假設(shè)第一個節(jié)點是最好的,作為主變量,進行全窗口搜索。通過零窗口搜索,判斷是否存在αβ的值,在此基礎(chǔ)上進行博弈樹的剪枝。其中,對節(jié)點進行排序是該算法至為關(guān)鍵的一步,這樣大大提高了搜索效率。所以本文采用了置換表和哈希表、歷史啟發(fā)增強、迭代深化等方法,極大地提高了算法的搜索效率[8]。 在搜索過程中,還增加了置換表和哈希表,如果計算過的價值,將會加入Hash表,并通過查找的方法判斷是否存在,如果存在就直接調(diào)用價值,這樣也大大加快了搜索過程;采用了歷史啟發(fā)方法增強通過已有的節(jié)點評分可更好地進行排序[9],價值高的節(jié)點排在前面,極大提高了搜索效率;與此同時,還通過迭代深化來加快節(jié)點排序的過程,過程中也一并進行時間的控制。在此基礎(chǔ)上,改進的PVS算法的偽碼參見如下。 FunctionPVS(intdepth,intalpha,intbeta){ if(depth<=0) returnvalue() generateAllMove() sort() makeMove() best=-PVS(depth-1,-beta,-alpha) unMakeMove() for(movei=1tomove.size()) if(best if(best>alpha) alpha=best makeMove() v=-PVS(depth-1,-alpha-1,-alpha) if(v best=-PVS(depth-1,-beta,-v) if(v>best) best=v unMakeMove() returnbest } 3實驗與結(jié)果 針對六子棋的估值設(shè)計和搜索算法,分別設(shè)計針對估值方法的對比和針對搜索方法的對比實驗。并分別使用先手和后手進行測試。 針對評估函數(shù),主要比較了基于“路”的評估方法和基于棋型的評估方法,其對比結(jié)果見表2。 由表2可以看出,在相同的對弈時間下,基于路的估值方法與基于棋型的估值方法相比較來說具有明顯的優(yōu)勢。 PVS算法與alpha-beta算法的對比結(jié)果見表3。 PVS算法與UCTS算法的對比結(jié)果見表4。 由表3和4可知,與alpha-beta算法和UCTS算法相比,PVS算法在棋力上占有一定的優(yōu)勢,無論是先手、還是后手,PVS的勝率都在85%以上。同時,因為雙方都使用相同的估值函數(shù),從棋力方面說明PVS算法更適合六子棋。 4結(jié)束語 本文針對PVS算法與alpha-beta算法和UCTS算法的對弈比較進行研究,結(jié)果表明PVS算法相較另外兩種算法在公平條件下有更好的搜索效率,在限制時間的博弈比賽中有更好的優(yōu)勢。同時,加入置換表和哈希表、歷史啟發(fā)增強、迭代深化等方法提高了PVS算法的搜索效率,而結(jié)合基于路的估值函數(shù)則極大地提高了分支的選擇效率。利用本文提出的算法開發(fā)的六子棋博弈程序獲得了2020年遼寧省大學生計算機博弈競賽六子棋項目冠軍,進一步驗證了該算法的有效性。 參考文獻 [1]鄧超.計算機圍棋中的搜索算法研究[D].昆明:昆明理工大學,2013. [2]WUIC,YENSJ.NCTU6winsConnect6tournament[J].InternationalClassicGuitarAssociation(ICGA)Journal,2006(3):157-158. [3]王靜文,吳曉藝.全國大學生計算機博弈大賽培訓教程[M].北京:清華大學出版社,2013. [4]王亞杰,邱虹坤,吳燕燕,等.計算機博弈的研究與發(fā)展[J].智能系統(tǒng)學報,2016,11(6):788-798. [5]徐心和,鄧志立,王驕,等.機器博弈研究面臨的各種挑戰(zhàn)[J].智能系統(tǒng)學報,2008,3(4):288-293. [6]何軒,洪迎偉,王開譯,等.機器博弈中搜索策略和估值函數(shù)的設(shè)計—以六子棋為例[J].電腦知識與技術(shù),2019,15(34):53-54,61. [7]李學俊,王小龍,吳蕾,等.六子棋中基于局部“路”掃描方式的博弈樹生成算法[J].智能系統(tǒng)學報,2015,10(2):267-272. [8]徐長明,馬宗民,徐心和.一種新的連珠棋局面表示法及其在六子棋中的應用[J].東北大學學報(自然科學版),2009,30(4):514-517. [9]YANGXue,LIHuayu,JIANGTianbo.Alpha-Beta-TSSinConnect6[C]//第27屆中國控制與決策會議.中國,青島:《控制與決策》編輯部,2015:746-751.

