基于灰色預測模型對白芍價格進行預測
趙宇靈,劉旭,孫盼盼,陳子晴
(銅陵學院數學與計算機學院,銅陵244061)
0 引言
2017 年國家統計局數據顯示,全國農民人口數量有57661 萬人,占比41.48%,且其中有不少人是貧困人口,他們的主要生活來源便是他們的土地種植出來的植物,其中有蔬菜、果樹、藥材……菜民和果農們所種植的蔬菜和果樹是他們賴以生存的承擔者,而其中蔬菜市場價格對農民近一年的生活質量都至關重要,同樣地,對于種植藥材的農民更是如此,且因有些藥材生長周期較長,更是決定著藥民的近幾年的生活質量(價格的大幅度波動會增加農民收益不確定性和其生產決策的難度,從黨中央、國務院對農產品市場監測和信息建設的多次提出,可以看出農產品市場價格波動是社會各界關注的熱點問題)。最近幾年,更是有越來越多的學者對農民所種植的作物進行價格預測與應用研究[1]。
亳州是全國最大的藥材集散地,是藥材之都,在此生活的人們大都以種植藥材來生活,其中藥材白芍更是因可以套中其他藥材或蔬菜而成為亳州農民們種植的首要選擇之一。從此方面看,如何科學有效地分析農產品市場價格的波動,準確預測農產品價格波動方向與幅度,對于指導農戶合理調整生產,規避市場風險,保障農產品市場穩定有序運行并有效控制物價超常波動具有重要的現實意義[2-3]。
而灰色系統理論作為于1982 年被鄧聚龍教授創立出的新理論,對解決一些“小數據、貧信息、不確定”的問題頗有自己的方法與手段[4],且在各領域中都得到了大量應用[5-8],尤其是在一些貧信息問題的預測之中。本文以影響白芍價格的因素權重為由建立AHP模型與灰色預測GM(1,1)模型結合[9-10],既可反映出影響白芍價格的主要因素排序,且由GM(1,1)預測出的結果能反映價格的整體趨勢,并有效削弱各類隨機波動因素的影響[1]。
1 研究思路與方法
通過層次分析法,將影響亳州市白芍價格這個多目標決策問題作為一個系統,把影響白芍價格的因素分解為多個目標或準則,進而分解為多指標(或準則、約束)的若干層次,通過定性指標模糊量化方法算出其(權數)和總排序,以作為目標(多指標)、多方案優化決策。在使用層次分析模型對影響白芍價格因素進行分析后,再使用灰色系統理論中的灰色預測建模理論對該問題進行模型建立,最后對其進行預測。這樣既能保證農民了解哪些因素影響對白芍價格影響較大,又能讓農民知曉在知道未來3 年的白芍價格后應該怎么對自家種植的白芍進行處理。
1.1 采用層次分析法對白芍價格影響因素進行分析
(1)構建AHP 遞階層次結構模型
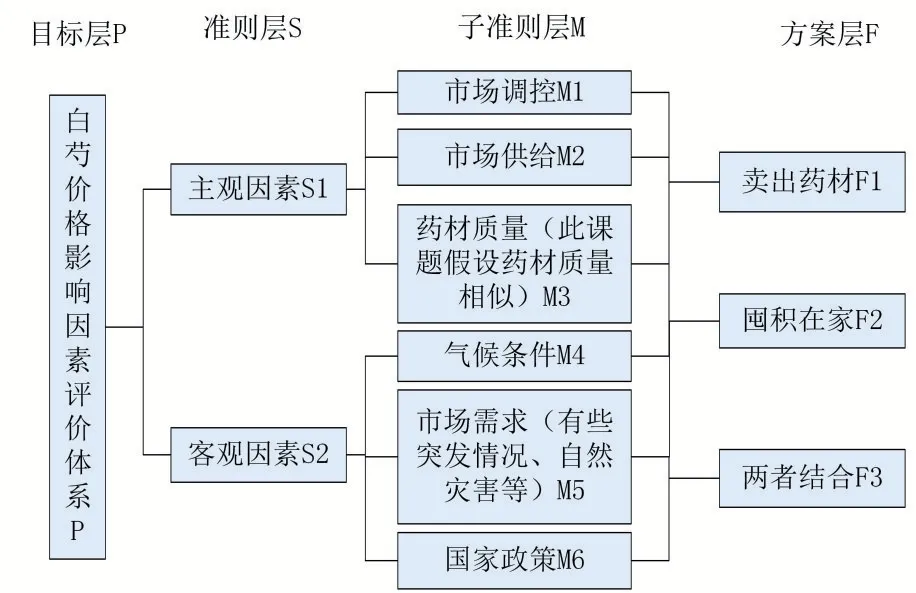
圖1
(2)構建比較判斷矩陣。對影響白芍價格的因素運用1~9 標度法進行比較,比較其相對權重,并算出其最大特征根。
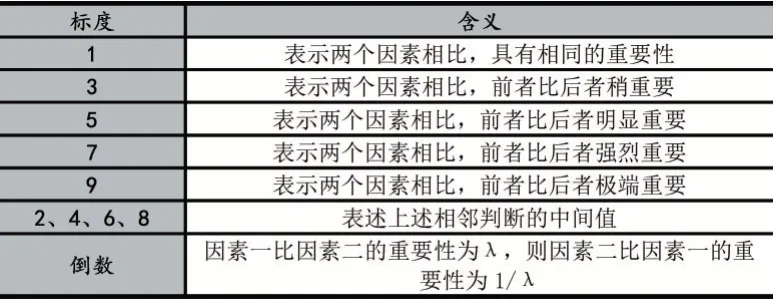
表1 1~9 標度法基本原理
(3)計算各層次相對權重及一致性檢驗
為了計算方便,將準則層內的因素細化到子準則層內,對子準則層各因素的重要性比較構造判斷矩陣并進行計算,所得判斷矩陣及相應計算結果如表2。
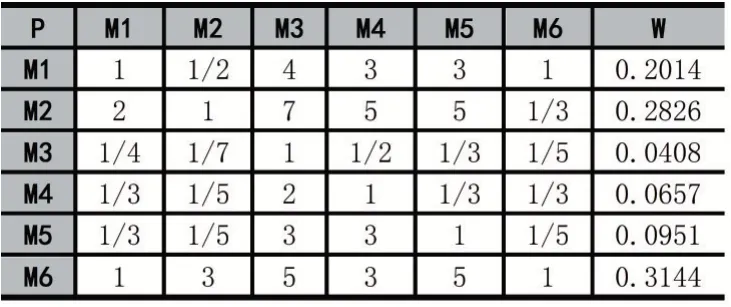
表2 判斷矩陣P-M 權重大小判斷矩陣及特征向量W 計算結果

表3 判斷矩陣Mi-F 權重大小判斷矩陣及特征向量W 計算結果(i=1,2,3,4,5,6)

表4 層次總排序計算結果
從該層次總排序計算結果表中可以看出,M6 >M2 >M1 >M5 >M4 >M3,即因素影響排序為:國家政策>市場供給>市場調控>市場需求>氣候條件>藥材質量;且在不同情況下,農民采取的最優措施排序依次為:兩者結合>賣出藥材>囤積在家。
接下來,我們可將AHP 模型得到的結果與灰色系統理論相結合對白芍價格數據進行處理并進行灰色預測。
1.2 運用灰色系統理論對白芍價格進行處理及預測
(1)數據生成處理,即時間序列的生成。
將歷年的白芍市場價格時間序列進行數據處理將其命名為X(0),為原始數據時間序列:

(式中(0)表示原始數據;m 表示時間序列,m ∈n)
為了避免原始數據的時間序列有太多的隨機因素,灰色系統預測通常將原始數據進行加工處理,即將統一數據的前i項元素累加生成新的數據列的第i列元素。此處我們采用一次累加的方法對數據進行處理,其第一次累加生成的數據列的表達式為:

同理可得第r 次累加生成的數據列為:

其緊鄰均值(MEAN)生成序列為:

其中,z(1)(k)=0.5x(1)(k)+0.5x(1)(k-1)(k=2,3,…,n)。
(2)灰色預測模型微分方程
本文從信息預測的角度來考慮,選用單序列一階線性模型——GM(1,1)模型來預測白芍價格,其灰色模型微分方程為:

a,b用為最小二乘法進行估計的參數,x(1)為原始數據x(0)的累加生成值。
(3)灰色預測模型
求解灰色模型微分方程即可得到其預測模型的離散形式,即:
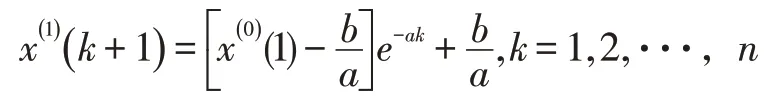
a,b用最小二乘法進行估計,即:
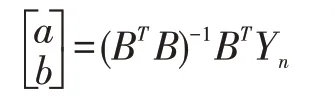
可以得到,預測模型公式為:
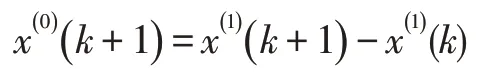
(4)殘差檢驗
檢驗該模型的合理性與正確性。通過判斷殘差平方和的大小來確定模型是否精確;若相對精度大于70%,則該模型合理;若模型相對精度不到70%,則該模型不合理。
2 實證分析與結果
通過在中藥材天地網的數據搜尋,整理得到亳州白芍市場白芍價格數據如表5。
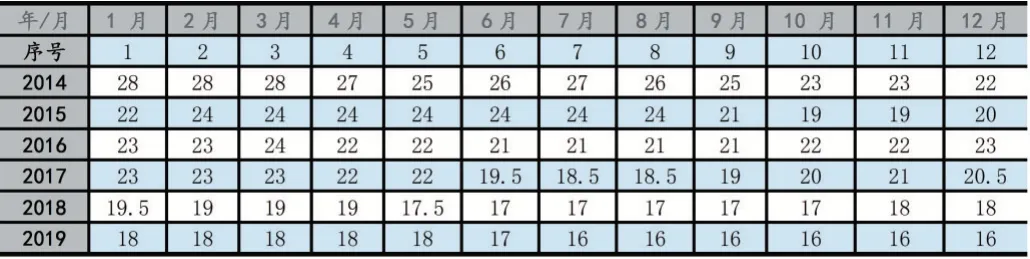
表5
2.1 AHP模型
通過第二部分研究思路及方法,我們已經可以得到在AHP 模型的運作之下,影響白芍價格的因素重要性排序依次為:兩者結合>賣出藥材>囤積在家。
所以,我們可根據該結果來進行后續白芍價格的預測。
2.2 灰色預測模型的建立
(1)整合數據

表6
(2)作一階累加處理
原始數據序列為:
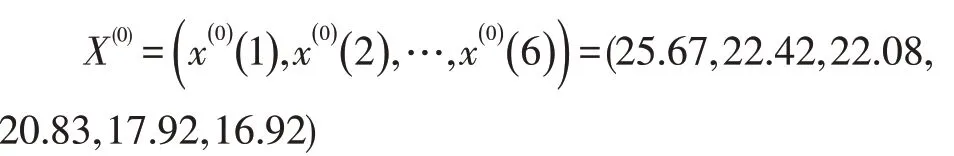
作一階累加處理后的序列為:

(3)建立GM(1,1)模型
時間響應式為:

其中發展系數a=0.0744,灰色作用量b=25.8938。
(4)殘差檢驗

表7
通過殘差檢驗可以看出,該模型精度遠大于70%,所以,該模型足夠精確。
2.3 預測結果
由以上模型及檢驗可以看出,該灰色GM(1,1)模型精度符合要求,所以可對數據往后年份進行預測,預測結果如表8。

表8
3 結語
本文創新地將AHP 層次結構模型與灰色預測模型相結合,針對一款民生問題——即藥材白芍的價格進行數據的處理與分析。通過實際探究得出:國家政策的變化是影響白芍價格波動的主要因素;在影響因素等其他條件的限制下,農民所能采取白芍處理的最好方式依次為:兩者結合>賣出藥材>囤積在家。接著運用灰色預測模型對實際數據進行預測與分析,發現在2014-2019 年亳州市白芍價格的數據基礎之上運用灰色預測模型,得到2020-2022 年亳州市白芍預測價格,可對農民接下來的種植計劃提供更多理論與數據依據,為農民解決一大難題。

