鐵路無縫線路極限狀態法和容許應力法設計對比研究

尹銀艷

(1.中鐵第四勘察設計院集團有限公司,武漢 430063； 2.鐵路軌道安全服役湖北省重點實驗室,武漢 430063)

美國、日本、俄羅斯等國家和歐洲以及我國建筑、公路、港口、水利水電等行業的結構設計規范，均采用以概率論為基礎的極限狀態法，概率極限狀態法是工程結構設計方法的發展趨勢[1-7]。為適應鐵路軌道技術的不斷發展，實現與國際接軌，進一步提高鐵路軌道設計的科學性，規范的計算理論從容許應力法向極限狀態法轉軌是十分必要的[8-12]。自2011年開始，原鐵道部和鐵路總公司相繼主持開展了鐵路工程結構設計標準由容許應力法向極限狀態法轉軌的基礎研究工作，于2015年頒布了Q/CR 9130—2015《鐵路軌道極限狀態法設計暫行規范》[13](以下簡稱“《暫規》”)。由于《暫規》發布時間很短，且由于是與現行設計規范并行，所以廣大鐵路工程設計人員對其關注度不高，對極限狀態設計法理解不深[8]。2018年正式發布Q/CR 9130—2018《鐵路軌道設計規范》(極限狀態法)[14](以下簡稱“《新規》”)。

本文針對福平鐵路閩江特大橋(68+128+68) m連續梁，分別采用《新規》中的極限狀態法和TB 10015—2012《鐵路無縫線路設計規范》[15](以下簡稱“《現規》”)中的容許應力法對橋上無縫線路進行設計計算，對比兩種設計方法檢算結果的主要技術指標。同時從福平、寧安、鄭萬、商合杭、合福等鐵路選取多個橋上無縫線路設計工點，通過對比兩種方法的檢算結果，分析《新規》極限狀態法對無縫線路設計的影響。

1 閩江特大橋無縫線路工點概況

福平鐵路閩江特大橋(68+128+68) m連續梁位于DK15+210.248～DK16+088.046處，福州端位于直線，平潭端位于R-1 600 m的曲線上，橋上采用有砟軌道，橋梁橋跨布置見圖1。以下采用《新規》中的極限狀態法進行無縫線路設計。

圖1 閩江特大橋橋跨布置示意(單位：m)

2 計算模型及參數

2.1 計算模型

橋上無縫線路縱向附加力計算采用梁軌相互作用的有限元分析模型[16-20]，如圖2所示。由于扣件阻力為非線性，計算軌道應力需要進行一系列的非線性分析，采用ANSYS通用軟件進行梁軌相互作用分析。

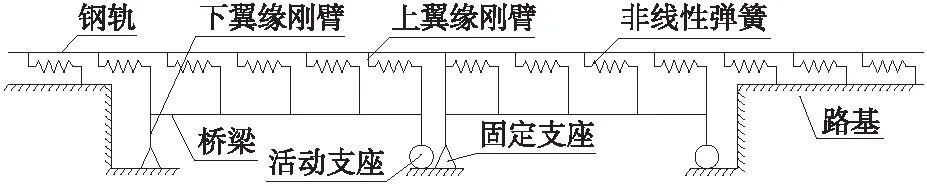
圖2 梁軌相互作用計算模型

2.2 計算參數

(1)鋼軌參數

福平鐵路鋼軌采用60 kg/m、100 m定尺長U75V無螺栓孔新鋼軌。60 kg/m鋼軌的截面特性如下：面積A=77.45 cm2；轉動慣量I=3 217 cm4；彈性模量E=2.1×105MN/m2，鋼軌鋼的線膨脹系數α=1.18×10-5/℃。

鋼軌屈服強度標準值按《新規》第4.2.3條規定取σs=472 MPa。

(2)鋼軌溫度

閩江特大橋所在區段最高軌溫61.7 ℃，最低-1.7 ℃，設計鎖定軌溫31 ℃。

(3)線路縱向阻力

采用新Ⅲ型橋枕，有砟軌道采用常阻力扣件時，線路阻力取道床阻力；采用小阻力扣件時，線路阻力取扣件阻力。單位長度道床縱向阻力見《新規》第4.2.5條規定。

有砟軌道采用彈條V型小阻力扣件、扣件節點間距為600 mm時，車輛下或者無載時縱向阻力取值8 kN/m/軌，機車下單位長度縱向阻力取值12.4 kN/m/軌。

(4)梁溫差

有砟軌道梁溫差取15 ℃。

(5)列車荷載

福平鐵路閩江特大橋位于福州至福州南區間，區段內為客運專線，列車荷載取CH3動車組荷載，軸重為17t，軸間距為2.5 m。

采用極限狀態法設計時，《新規》中關于無縫線路計算模型及參數取值的相關規定與《現規》一致。

3 橋上無縫線路設計

閩江特大橋(68+128+68) m連續梁考慮設置小阻力方案：連續梁橋上距連續梁梁端50 m范圍鋪設新Ⅲc型橋枕(1 667根/km)及其配套彈條Ⅴ型小阻力扣件，其余地段鋪設新Ⅲ型橋枕(1 667根/km)及其配套彈條Ⅱ型扣件。按照以上設置小阻力扣件、不設伸縮調節器方案，計算無縫線路縱向力。

3.1 軌道附加力計算

福平鐵路閩江特大橋鋼軌伸縮力計算結果如圖3所示，鋼軌伸縮力最大值為469.8 kN，換算應力為60.7 MPa。

鋼軌制動力計算結果如圖4所示，最大值為370.2 kN，換算應力為47.8 MPa。

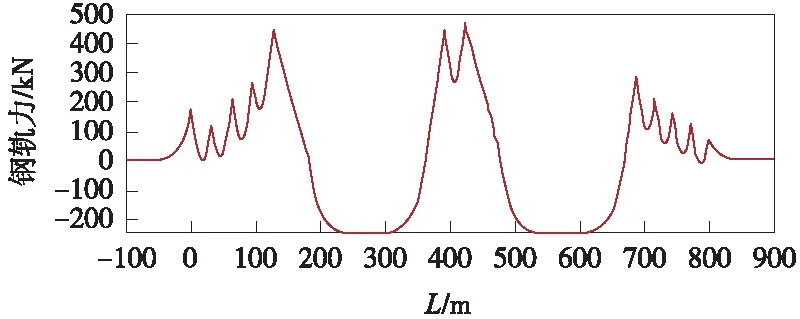
圖3 鋼軌伸縮力

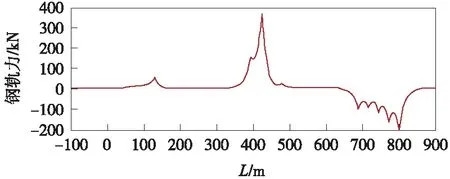
圖4 鋼軌制動力

3.2 鋼軌動彎應力計算

鋼軌在車輪動荷載作用下的鋼軌動彎矩計算

Md=M0(1+α+β)

(1)

式中，M0為鋼軌截面的靜彎矩；α為速度系數；β為偏載系數。

軌底邊緣最大動彎應力為

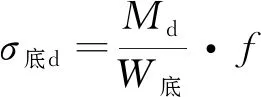
(2)

式中，Wg為軌底的截面參數，cm3；f為軌道橫向水平力系數。

對于鋼軌動彎應力計算中的速度系數、偏載系數和橫向水平力系數，《新規》與《現規》規定取值一致。經計算，福平鐵路閩江特大橋鋼軌軌底動彎應力σ底=141.5 MPa。

3.3 極限狀態法檢算

(1)鋼軌強度承載能力極限狀態

無縫線路承載能力極限狀態設計按式(3)進行鋼軌強度檢算，并按式(4)計算溫降限值。

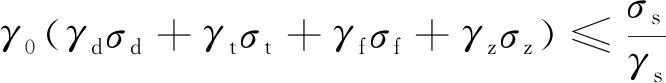
(3)

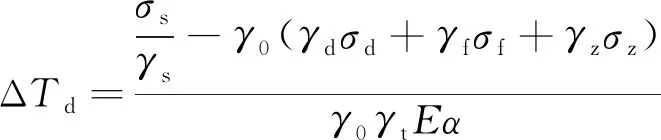
(4)

式中，γ0為結構重要性系數；σd和γd分別為軌底邊緣動彎應力的標準值和分項系數；σt和γt分別為鋼軌最大溫度應力的標準值和分項系數；σf和γf分別為鋼軌最大附加應力的標準值和分項系數；σz和γz分別為鋼軌牽引(制動)應力的標準值和分項系數；σs和γs分別為鋼軌屈服強度的標準值和分項系數；E為鋼軌彈性模量；α為鋼軌線膨脹系數。

將福平鐵路閩江特大橋無縫線路縱向力計算結果代入式(4)，得到溫降限值為46.45 ℃。初步定的設計鎖定軌溫為31 ℃，鎖定軌溫范圍為(31±5) ℃，則最大溫降幅度ΔTdmax=31+5-(-1.7)=37.7 ℃<46.45 ℃，即最大溫降幅度小于溫降限值，無縫線路鋼軌強度滿足要求。

(2)鋼軌斷縫

無縫線路承載能力極限狀態設計按式(5)進行鋼軌斷縫檢算。

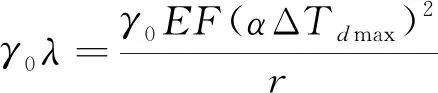
(5)

式中，λ為鋼軌斷縫，F為鋼軌斷面面積，r為線路縱向阻力，取小阻力扣件阻力值。

按上式計算得斷縫40.2 mm<λ0=70 mm，故斷縫檢算滿足要求。

(3)無縫線路穩定性正常使用極限狀態

無縫線路正常使用極限狀態設計按式(6)進行無縫線路穩定性檢算，并按式(7)計算溫升限值。

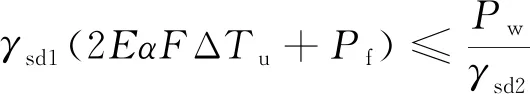
(6)

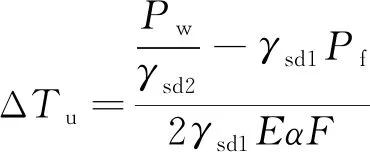
(7)

式中，γsd1、γsd2為計算模型不定性系數；Pw為臨界溫度壓力；Pf為單線伸縮力或撓曲力的最大值。

首先，根據《新規》附錄B計算出溫度壓力Pw=3 993.955 kN。代入式(7)計算得溫升限值54.8 ℃。

設計鎖定軌溫為31 ℃，鎖定軌溫范圍為(31±5) ℃，則最大溫升幅度ΔTumax=61.7-(31-5)=35.7 ℃<54.8 ℃，最大溫升幅度小于溫升限值，故無縫線路穩定性檢算滿足要求。

3.4 容許應力法檢算

(1)鋼軌強度

容許應力法計算，鋼軌附加縱向應力取伸縮應力或撓曲應力的最大值，即縱向附加力=(469.8+370.2)/77.45×10=108.457 MPa，而鋼軌軌底最大動彎拉應力為141.5 MPa。故鋼軌容許應力[σ]=σs/1.3=363.08 MPa。

按式(8)確定允許溫降

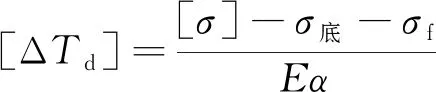
(8)

將鋼軌應力代入式(8)得到允許溫降為45.7 ℃，最大溫降幅度Tdmax=37.7 ℃<45.7 ℃，故無縫線路鋼軌強度滿足要求。

(2)無縫線路穩定性

計算得臨界溫度壓力Pw=3 993.955 kN，則兩股鋼軌的允許溫度壓力[P]=Pw/1.3=3 072.273 kN。

按式(9)確定允許溫升

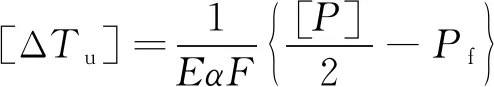
(9)

將鋼軌應力代入式(9)得到允許溫升為55.6 ℃，最大溫升幅度ΔTumax=35.7 ℃<55.6 ℃，故無縫線路穩定性檢算滿足要求。

(3)鋼軌斷縫

鋼軌斷縫可按式(10)檢算

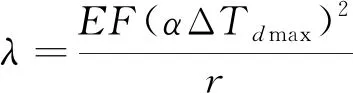
(10)

按上式計算得斷縫40.2 mm<λ0=70 mm，故斷縫檢算滿足要求。

3.5 兩種方法主要技術指標對比

本橋無縫線路檢算的主要技術指標為容許溫升和容許溫降、斷縫值，如表1所示。對于溫升，極限狀態法較容許應力法的溫升容許值相差-1.4%；而溫降方面，極限狀態法較容許應力法的溫升容許值相差1.6%；斷縫檢算相同。由此引起的橋上鋪設方案沒有變化，均在連續梁及兩側各兩跨簡支梁鋪設小阻力扣件即可，即橋上的軌道工程數量沒有變化。

表1 福平鐵路閩江特大橋(68+128+68) m連續梁無縫線路技術指標對比

4 多座鐵路橋梁無縫線路設計對比分析

為進一步研究《新規》中的極限狀態設計法對無縫線路設計結果的影響，分別從福平、寧安、鄭萬、商合杭、合福等多個鐵路選取典型工點，分別采用極限狀態法和容許應力法進行無縫線路結構檢算。

4.1 計算工況

將本文選取的多個鐵路項目橋上無縫線路工點概況匯總，列于表2中，計算工況覆蓋了不同鐵路等級、不同設計速度、不同軌道結構型式、不同橋梁跨度。

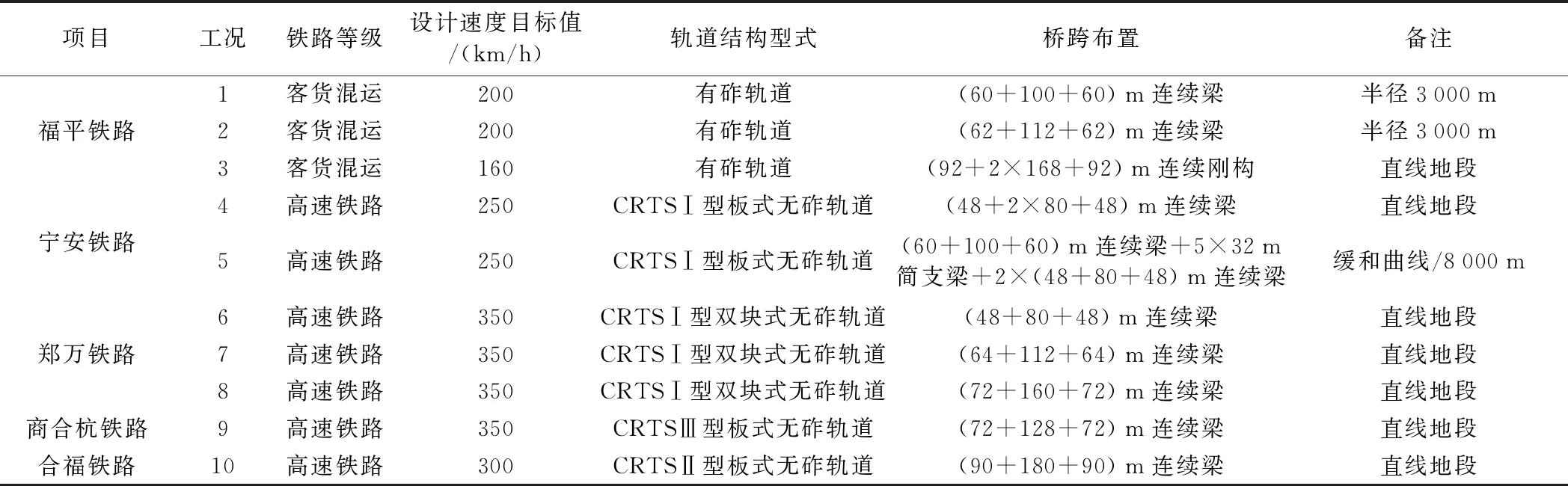
表2 多個鐵路項目橋上無縫線路工點信息

4.2 無縫線路檢算主要技術指標對比

分別采用《新規》的極限狀態法和《現規》的容許應力法，對所選工況的無縫線路進行試設計。限于篇幅，本文直接列出所有工況采用極限狀態法和容許應力法兩種方法的檢算結果，如表3所示。

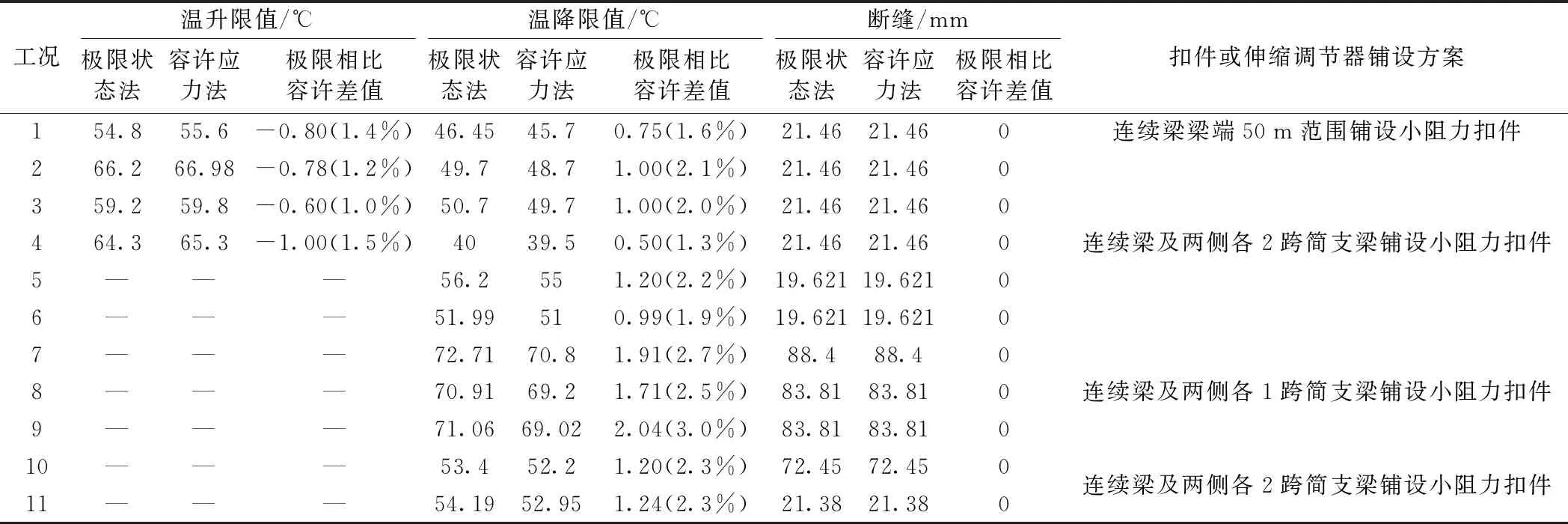
表3 橋上無縫線路極限狀態法和容許應力法設計結果對比

將上述工況下，采用《新規》中的極限狀態法和《現規》中的容許應力法得到的無縫線路檢算結果繪制對比圖，如圖5、圖6所示。從本文選取的工況的計算結果可以發現：

(1)極限狀態法計算的最大溫降普遍比容許應力法的溫降限值大，最多增加2.0 ℃，增加幅度最大為3.0%；

(2)極限狀態法計算的最大溫升普遍比容許應力法的溫升限值小，最多減小1 ℃，減小幅度最大為1.5%；

(3)極限狀態法和容許應力法的斷縫檢算無差別。

根據以上各工點的計算結果，由于采用兩種方法計算后均未引起扣件或伸縮調節器的鋪設方案變化，從軌道工程的造價比較，兩者的經濟指標幾乎相同，沒有變化。

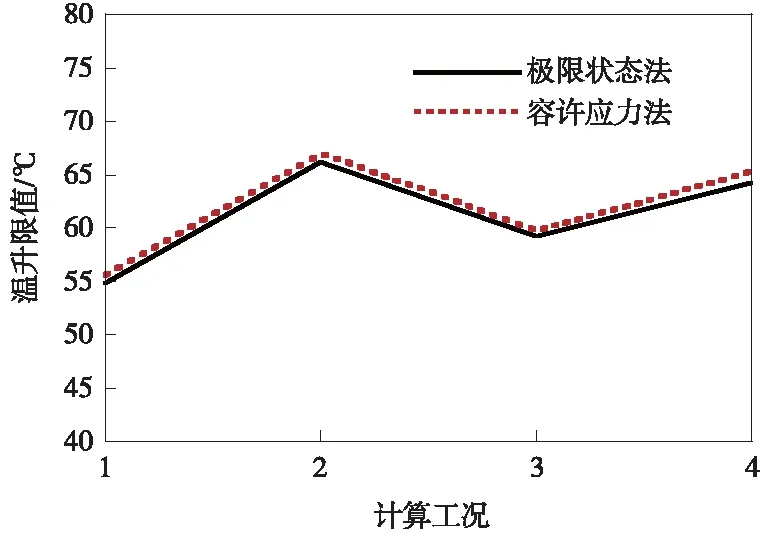
圖5 兩種方法的溫升限值對比

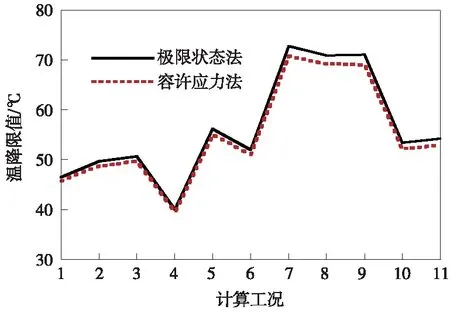
圖6 兩種方法的溫降限值對比

5 結論

從多個鐵路項目中選取橋上無縫線路設計工點，分別采用《新規》的極限狀態法和《現規》的容許應力法進行無縫線路設計計算，對比兩種設計方法檢算結果的主要技術指標。得出以下結論。

(1)對所選工況而言：極限狀態法計算的最大溫降普遍比容許應力法的溫降限值大，最多增加2.0℃，增加幅度最大為3.0%；而極限狀態法計算的最大溫升普遍比容許應力法的溫升限值小，最多減小1℃，減小幅度最大為1.5%；兩種方法的斷縫檢算無差別。

(2)對所選工況而言：采用兩種方法計算后均未引起扣件或伸縮調節器的鋪設方案變化，從軌道工程的造價來說，兩者的經濟指標相同。

(3)采用《新規》極限狀態法與《現規》容許應力法兩種方法的無縫線路檢算結果不完全一致，特殊工況下建議采用極限狀態法進行無縫線路設計時，同時采用容許應力法進行校核。

(4)研究成果可為鐵路無縫線路極限狀態法設計研究和推廣應用提供參考。