基于山嶺隧道探孔流量的富水破碎構(gòu)造帶水頭預測方法

于晨昀,項彥勇,孫俊豪

(1.中鐵工程設計咨詢集團有限公司,北京 100055； 2.北京交通大學土木建筑工程學院,北京 100044)

引言

山嶺隧道修建過程中，會遇到開挖面前方存在富水斷層構(gòu)造帶[1]、高壓富水斷裂帶[2]、富水巖溶[3-4]等富水破碎構(gòu)造帶的復雜地質(zhì)情況。隧道施工期穿越上述不良地質(zhì)時存在突水涌泥等施工風險，且隧道運營期承擔的外水壓力與水頭高度密切相關。確定富水破碎構(gòu)造帶的水頭高度對保障山嶺隧道施工與運營安全具有重要意義。

為確保隧道穿越富水破碎構(gòu)造帶的施工安全，需進行超前地質(zhì)預報。超前地質(zhì)探孔是常用的超前地質(zhì)預報手段，采用地質(zhì)鉆機鉆孔并安裝流量計，可以比較直觀的探明開挖面前方鉆孔所經(jīng)部位的地層巖性、巖體完整程度和地下水發(fā)育情況[5-6]，連續(xù)鉆探時探孔有效長度一般每循環(huán)不超過50 m。

吳建、朱彬彬等[7-8]開展隧洞涌水量預測計算及方法研究進展，楊建軍[9]根據(jù)探孔的噴水距離和噴水量對可能發(fā)生突水的類型進行判斷，結(jié)合噴水量及噴水距離判斷突水情況并制定相應的防水方案及措施；袁真秀等[10]在圓梁山隧道高壓富水地區(qū)，利用平行導洞超前探孔的涌水特征，對前方溶洞的尺度和連通性進行判斷；段慶偉等[11]基于滲流理論推導出施工期隧道開挖后圍巖內(nèi)水壓力分布的解析解，研究遠場穩(wěn)定水頭與遠場穩(wěn)定水頭半徑的相互關系。何志軍等[12]推導了含水層中橢圓形隧道的近似解析解，用于計算隧道周邊水頭和孔隙水壓分布。姚橋礦和李明山[13]、王革純等[14]、侯恩科等[15]分別對鉆孔涌水量計算方法進行了探討。

目前，國外針對隧道超前鉆孔排水與圍巖滲流相互作用問題已開展研究，如，Hong等[16]研究了超前排水鉆孔的水力能力問題；Zingg & Anagnostou[17-18]在孔壁處于大氣壓力假設下，考慮孔壁水壓變化，采用理論方法與數(shù)值模擬，研究了超前鉆孔排水與圍巖滲流的相互作用及其對隧道開挖面穩(wěn)定性的影響。

隧道突水風險與開挖面前方水頭高度密切相關[19]，但現(xiàn)有研究大多是關于隧道開挖面前方涌水量預測，對開挖面前方水頭高度預測研究較少。考慮圍巖滲透性的影響，研究提出通過探孔涌水量預測隧道開挖面前方富水破碎構(gòu)造帶水頭高度的3種預測方法：簡化理論方法；軸對稱穩(wěn)態(tài)與瞬態(tài)滲流數(shù)值模擬方法；基于穩(wěn)態(tài)滲流數(shù)值模擬數(shù)據(jù)的近似擬合方法。

1 探孔-圍巖穩(wěn)態(tài)流動的廣義伯努利理論

1.1 探孔穩(wěn)態(tài)流動的無滲漏管流理論

超前探孔壁面穩(wěn)定，圍巖滲透系數(shù)較小，可近似地認為探孔與圍巖之間無水力聯(lián)系，如圖1所示。假設探孔內(nèi)水流為無滲漏的滿管水流，利用伯努利方程[20]，可以得出

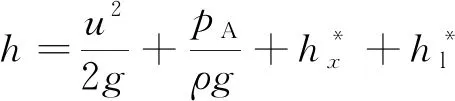
(1)

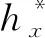
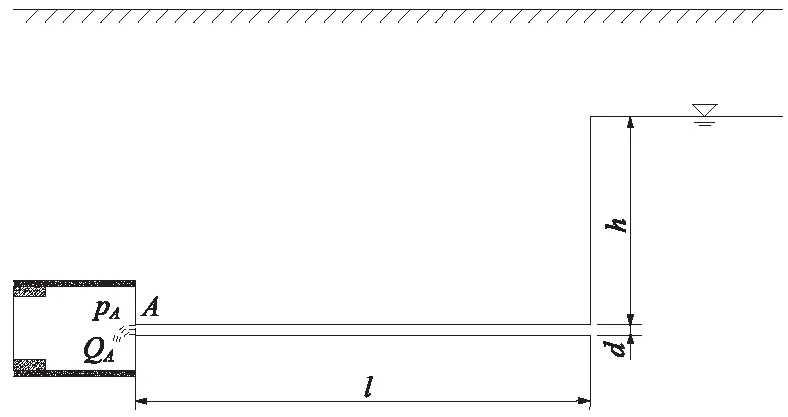
圖1 超前水平探孔的無滲漏管流模型

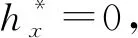
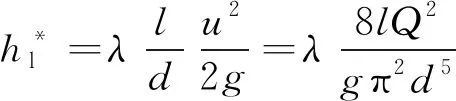
(2)

式中，Q為探孔出水口流量，Q=uπd2/4；l和d分別為探孔的有效長度(隧道開挖面到前方富水破碎構(gòu)造帶邊界的水平距離)和直徑；λ為沿程阻力系數(shù)，其與管流的流態(tài)(層流或紊流)和孔壁的粗糙度有關。根據(jù)流體力學理論[20]，采用雷諾數(shù)Re=ρud/μ來判別層流或紊流(μ為水的動力黏度，對于常溫地下水，可取μ=1.005×10-3Pa·s)，一般以Re=2 300作為層流與紊流的分界，當Re<2 300時管流為層流，沿程阻力系數(shù)為λ=64/Re；當Re>2 300時管流為紊流，可根據(jù)雷諾數(shù)Re和管壁相對粗糙度e/d(e為管壁粗糙度)由莫迪(Moody)圖確定沿程阻力系數(shù)λ值。

假設管流在近端為自由排水，壓強pA=0，并將式(2)代入式(1)，可得

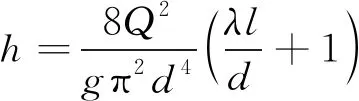
(3)

由式(3)可見，探孔的遠端水頭分別與流量平方、長度、沿程阻力系數(shù)成正比。

1.2 探孔-圍巖穩(wěn)態(tài)流動的均勻滲漏管流理論

超前探孔壁面穩(wěn)定，圍巖滲透系數(shù)較大，探孔與圍巖之間的水力聯(lián)系不可忽略，如圖2所示。假設探孔內(nèi)的水流為有滲漏的滿管水流，基于伯努利方程，可以得出

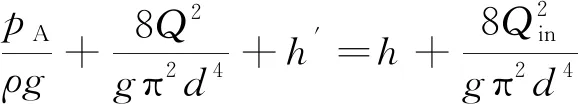
(4)

式中，h′為管流的平均水頭損失；Qin為管流在遠端的流量。其余符號的定義同前。

基于質(zhì)量守恒原理，Qin=Q+Ql，代入式(4)，可得

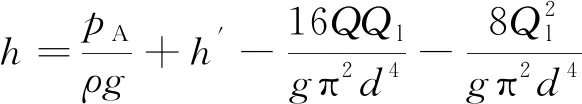
(5)

式中，Ql為管流全長的滲漏流量。

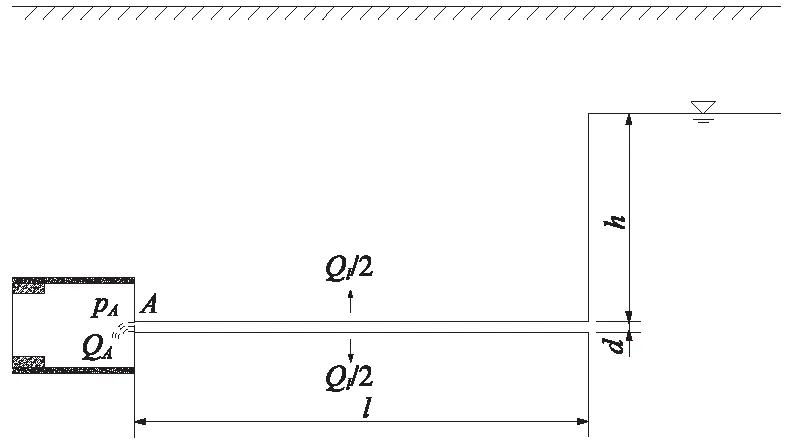
圖2 探孔-圍巖的均勻滲漏管流模型

2 探孔-圍巖穩(wěn)態(tài)滲流數(shù)值模擬與參數(shù)分析

2.1 探孔-圍巖軸對稱穩(wěn)態(tài)滲流有限元模型

探孔壁面穩(wěn)定，如前方富水破碎帶水頭較高，則地下水重力梯度與壓力梯度的影響相比很小，可以忽略不計，近似認為水力梯度等于水壓梯度，滲流關于探孔軸線對稱。

采用有限元軟件Midas GTS NX，建立任意軸對稱截面的穩(wěn)態(tài)滲流有限元模型，如圖3所示。其中，隧道高12 m，探孔直徑和長度分別為0.1 m和30 m，模型上、下邊界到探孔軸線的距離均為50 m，富水破碎構(gòu)造帶位于探孔的遠端，水頭高度50 m。網(wǎng)格的密集程度與水力梯度的分布特征相對應，較高水力梯度的區(qū)域采用較密集網(wǎng)格，較低水力梯度的區(qū)域采用較稀疏網(wǎng)格。

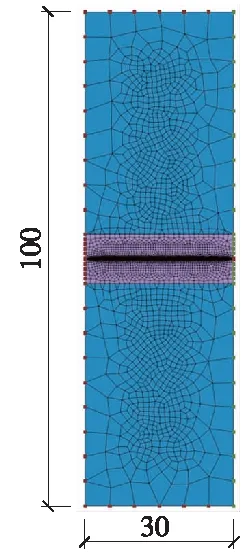
圖3 探孔-圍巖穩(wěn)態(tài)滲流的軸對稱有限元模型(單位：m)

基于滲流的軸對稱特征，設定有限元模型邊界條件為：(1)左邊界，壓力水頭為零；(2)右邊界，在鉆孔遠端(入水口)的壓力水頭為50 m，其他位置不透水，即探孔遠端是唯一的入水口；(3)上邊界，不透水；(4)下邊界，不透水。

有關計算參數(shù)如表1所示，其中，d為探孔直徑；k為圍巖的滲透系數(shù)；lr為探孔的有效長度；h為水頭高度。

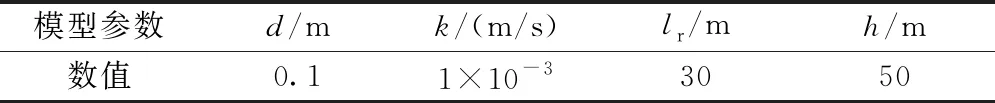
表1 有限元模型參數(shù)

由于實際探孔出水量遠大于圍巖滲水量，將探孔模擬為滲透性遠高于圍巖滲透性的多孔介質(zhì)，則探孔節(jié)點的軸向達西流速qx與探孔截面積的乘積即為探孔出水口流量Q，Q=qxπd2/4。

2.2 數(shù)值模擬的參數(shù)影響分析

探孔-圍巖的壓力水頭分布云圖如圖4所示，其中探孔出水口壓力水頭為0 m，探孔入水口壓力水頭為50 m，表明模型的流動達到了穩(wěn)態(tài)流動。

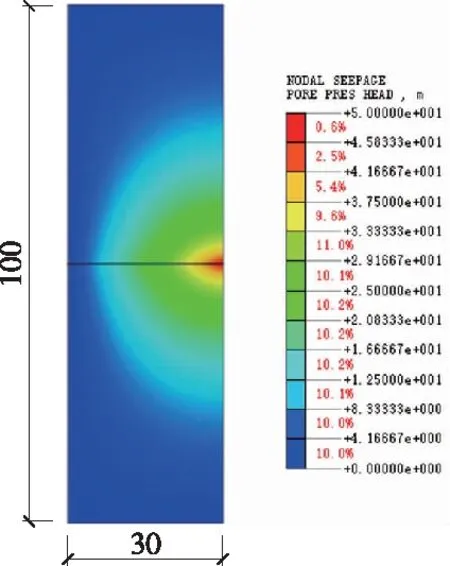
圖4 穩(wěn)態(tài)壓力水頭云圖(單位：m)

圖5為探孔上、下邊界壁面上法向(y軸)達西流速qy沿探孔軸線(x軸)的分布曲線。x軸和y軸原點均位于探孔在隧道開挖面處中心，qy為正值時表示向上流動、為負值時表示向下流動。由圖5可見，探孔內(nèi)水流從進水口處開始向圍巖滲漏，滲漏速度隨流動距離的增加(x減小)而逐漸減小至零，之后探孔內(nèi)的水流得到圍巖水流的補給(負滲漏，流速較低)，補給速度隨流動距離的增加(x減小)而逐漸增加，至出水口處達到最大值，零滲漏點到出水口的距離為17.7 m(與有效長度之比為0.59)。

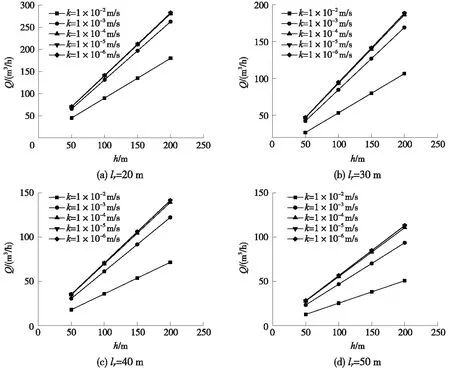
圖7 不同探孔有效長度lr的Q-h曲線(穩(wěn)態(tài))

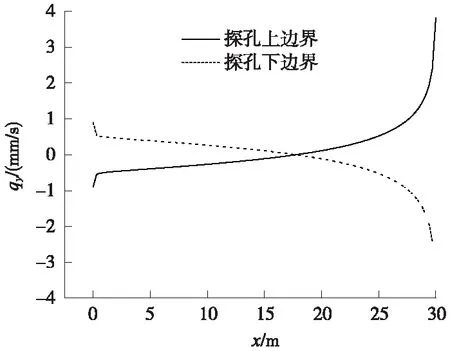
圖5 探孔壁面法向(y軸)穩(wěn)態(tài)達西流速沿軸線(x軸)分布曲線

為進行參數(shù)影響分析，根據(jù)上述數(shù)值模擬結(jié)果，考慮探孔-圍巖內(nèi)穩(wěn)態(tài)滲流模型如圖6所示，其中，A為探孔在隧道開挖面處截面；B為探孔在富水破碎構(gòu)造帶近邊界處截面；C為探孔在富水破碎構(gòu)造帶內(nèi)部某處截面；O為探孔在滲漏流量為零處截面(位置待定)。探孔內(nèi)的水流在OA段為負滲漏(即得到圍巖水流補給)，在OB段為正滲漏(即向圍巖滲漏)，BC段對AB段及圍巖內(nèi)的流動無影響。

分別取水頭高度h為50，100，150，200 m；探孔圍巖滲透系數(shù)k為10-2，10-3，10-4，10-5，10-6m/s；探孔有效長度lr為20，30，40，50 m，共計4×5×4=80個工況進行數(shù)值模擬，分析參數(shù)對探孔出水口流量Q與水頭高度h關系的影響特征。

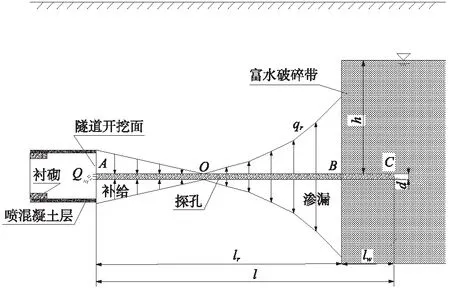
圖6 探孔-圍巖內(nèi)的穩(wěn)態(tài)滲流模型

圖7為探孔有效長度lr分別取20，30，40，50 m時，與不同圍巖滲透系數(shù)值相對應，探孔出水口流量Q與水頭高度h之間的關系曲線。可見，對于設定的k和lr，Q隨h的增大呈線性增大趨勢；對于設定的lr，Q隨k的減小而增大，隨h增大的速率同時增大；當k取值為10-4m/s及以下時，對Q-h關系基本沒有影響。

圖8為水頭高度h=50 m時，與不同圍巖滲透系數(shù)k值相對應，探孔出水口流量Q隨探孔有效長度lr的變化曲線。可見，對于設定的h和k，Q隨lr的增大以逐漸降低的速率非線性地減少；對于設定的h，Q隨k減小而增大；當k取值為10-4m/s及以下時，對Q-lr關系基本沒有影響。

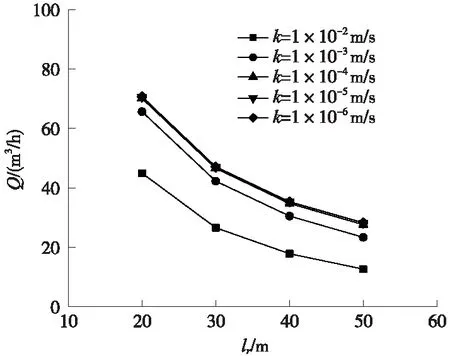
圖8 水頭高度h=50 m時Q-lr曲線(穩(wěn)態(tài))

圖9為圍巖滲透系數(shù)k不同取值時，探孔水流補給段長度比lOA/lr隨前方富水破碎構(gòu)造帶水頭h的變化。可見，對于設定的k值，lOA/lr隨h的增大以逐漸降低的速率非線性地減小；對于設定的h值，lOA/lr隨k減小呈非線性地減小趨勢。

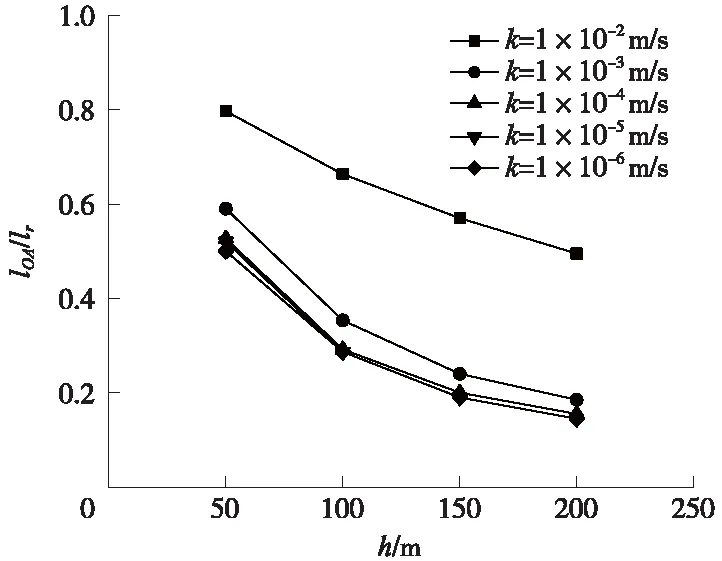
圖9 lOA/lr-h-變化曲線(穩(wěn)態(tài))

圖10為圍巖滲透系數(shù)k不同取值時，探孔出水口流量Q與入水口流量Qin之比。可見，對于設定的k值，Q/Qin與h無關；當k減小時，Q/Qin增大(注意，Q/Qin必須≯1)；當k取值為10-4m/s及以下時，Q/Qin趨于1，即探孔出水口流量與入水口流量相等，基本上無滲漏與補給。

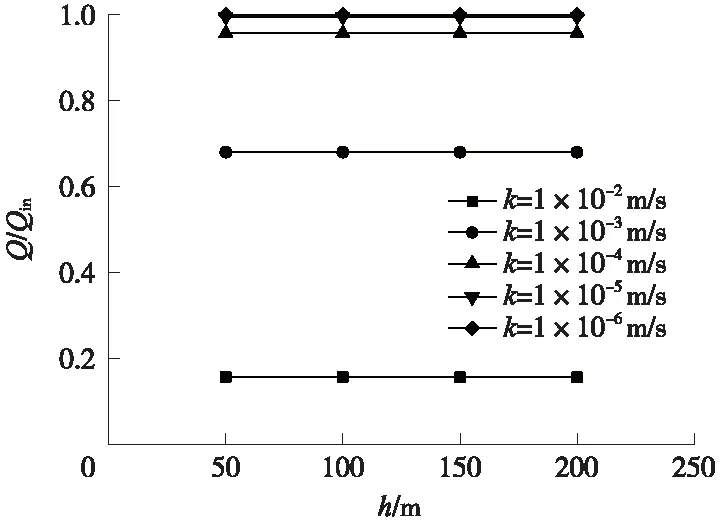
圖10 Q/Qin隨h的變化曲線(穩(wěn)態(tài))

綜上所述，水頭高度h與探孔出水口流量Q之間，因受達西滲流模型所控而呈線性關系；探孔遠端滲漏段長度、滲漏流量和探孔近端補給段長度、補給流量均受制于探孔有效長度lr和探孔圍巖滲透系數(shù)k，對h-Q關系的斜率及其變化特征產(chǎn)生影響。

3 探孔穩(wěn)態(tài)出水流量-前方富水破碎構(gòu)造帶水頭高度擬合式

3.1 擬合式的建立

由上節(jié)數(shù)值模擬結(jié)果可見，對于給定的探孔有效長度lr和圍巖滲透系數(shù)k，探孔出水口流量Q與水頭高度h之間呈線性正比例關系，一般可表示為

Q=α(lr，-lgk)h

(6)

式中，α(lr，-lgk)為比例系數(shù)，是探孔有效長度lr和探孔圍巖滲透系數(shù)k的函數(shù)(當流量單位以m/s表示時，圍巖滲透系數(shù)k值較小，為便于擬合，將k表示成常用對數(shù)的負數(shù))。

利用上節(jié)數(shù)值模擬所得數(shù)據(jù)，采用二元二次多項式的函數(shù)形式，通過最小二乘法優(yōu)化，得到Q與h之間的擬合關系式

(7)

式中，c1、c2、c3、c4、c6、c6代表擬合系數(shù)，如表2所示。

表2 擬合系數(shù)取值

3.2 擬合式與無滲漏管流理論公式對比

考慮常溫地下水，把無滲漏管流理論公式(3)與擬合式(7)進行對比。有關參數(shù)取值如表3所示(圍巖滲透系數(shù)取值很小)，計算結(jié)果對比如圖11所示。

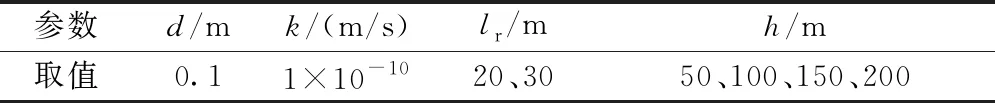
表3 對比數(shù)值擬合式與無滲漏管流理論式的參數(shù)取值

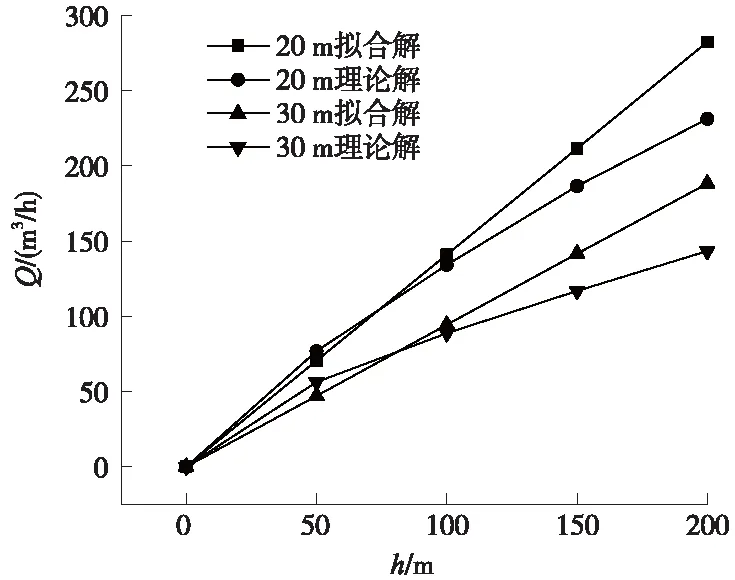
圖11 不同探孔有效長度lr(k很小)擬合式(7)與理論式(3)對比曲線

由圖11可見，如果圍巖滲透系數(shù)值很小，無論探孔有效長度lr為何值，只要水頭高度h≯100 m，擬合式(7)與理論式(3)間無顯著差別。但如果h超過100 m，則由擬合式(7)得到的探孔穩(wěn)態(tài)出水流量明顯大于理論式(3)，且差別隨h的增大而逐漸增大。

4 探孔瞬態(tài)涌水的數(shù)值模擬與分析

采用圖3所示的有限元模型及邊界條件，按表1選取參數(shù)值，對探孔-圍巖內(nèi)的軸對稱瞬態(tài)滲流進行數(shù)值模擬，分析探孔出水口流量與水頭高度的關系和穩(wěn)態(tài)時間與巖體滲透系數(shù)的關系。其中，如果在1個時間步長內(nèi)，探孔出水口流量的相對變化率≯0.5%，即認為流場已經(jīng)達到穩(wěn)態(tài)。

如圖12所示，在任意給定時刻，探孔出水口流量Q與水頭高度h間均為線性正比例關系，且Q-h的斜率隨著時間t的增大而增大，在穩(wěn)態(tài)時達到最大值。

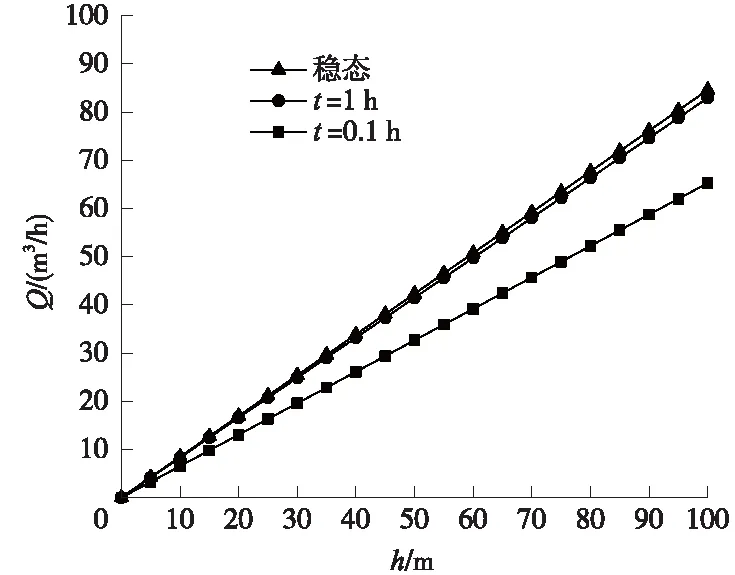
圖12 不同時刻的Q-h關系曲線

如圖13所示，對于給定的探孔有效長度lr，隨著圍巖滲透系數(shù)k增大，達到穩(wěn)態(tài)所需的時間t先增加、后減少；且隨著lr值增大，滲漏和補給的作用增大，對穩(wěn)態(tài)時間的影響也越顯著。

圖13 圍巖滲透系數(shù)對達到穩(wěn)態(tài)所需時間的影響

5 結(jié)論

在山嶺隧道工程中確定富水破碎構(gòu)造帶的水頭高度對降低隧道施工期突水突泥等災害風險，保證隧道運營期襯砌結(jié)構(gòu)安全具有重要意義。針對隧道超前探孔出水口流量Q與前方富水破碎構(gòu)造帶水頭高度h間的關系問題，基于伯努利方程得到了簡化理論關系式；通過隧道開挖面前方富水破碎構(gòu)造帶高水頭工況下探孔-圍巖軸對稱穩(wěn)態(tài)及瞬態(tài)滲流的數(shù)值模擬，得到了基于模擬結(jié)果的擬合關系式，進行參數(shù)影響分析，并與簡化理論關系式進行對比。通過研究得到以下結(jié)論。

(1)探孔穩(wěn)態(tài)或瞬態(tài)出水口流量與水頭高度之間呈線性正比例關系，比例系數(shù)隨探孔有效長度和圍巖滲透系數(shù)的增大而減小。

(2)當圍巖滲透系數(shù)較大時(>10-4m/s)，探孔內(nèi)的穩(wěn)態(tài)水流出現(xiàn)兩段不同的邊界面滲流情況，一段是在遠端一定長度內(nèi)的滲漏，另一段是在近端一定長度內(nèi)的補給。

(3)圍巖滲透系數(shù)較小時(<10-4m/s)，對探孔穩(wěn)態(tài)出水流量與水頭高度間關系無影響；

(4)探孔-圍巖滲流由瞬態(tài)達到穩(wěn)態(tài)所需的時間與水頭高度無關，但隨圍巖滲透系數(shù)的增大呈先增大、后減小趨勢，且這種影響隨探孔有效長度的增大而增強。

(5)對于探孔有效長度，如圍巖滲透系數(shù)很小，當水頭高度≯100 m時，擬合關系式與簡化理論關系式之間沒有顯著差別，但當水頭高度超過100 m，擬合關系式的探孔穩(wěn)態(tài)出水流量明顯大于簡化理論關系式出水流量。