基于F-score的特征選擇算法在多分類問題中的應用

秦喜文, 王 芮, 于愛軍， 董小剛*, 張斯琪

(1.長春工業大學 數學與統計學院， 吉林 長春 130012;2.北京首鋼國際工程技術有限公司， 北京 100043)

0 引 言

為了提高機器學習在分類問題上的準確性和效率，一些研究者已經開始將特征選擇算法與機器學習算法相結合。通過選擇重要的相關特征來降低計算成本，使得計算過程更加準確和易于理解。

特征選擇可以通過過濾器、包裝器或嵌入方法進行。過濾器方法為每個特征分配一個重要值以構建一個排名，得分最高的特征是與數據類最密切相關的。這種方法可以使用與算法無關的技術，如F-score[1]，以及基于信息度量的數據驅動變量選擇方法，如聯合互信息和正則化互信息等[2-3]。包裝器方法根據搜索算法確定的給定特征子集中分類器的性能來選擇特征。選擇分類器后，若干特征子集將用作分類器的輸入數據，然后選擇精度最高的特征子集。嵌入式方法將特征選擇融合在模型訓練的過程中，比如決策樹在分枝的過程中，就是使用嵌入式特征選擇方法，其內在還是根據某個度量指標對特征進行排序。 同時，隨機森林中的特征重要性排序也是嵌入式方法的一種。

機器學習已有近70年的發展歷史，隨著信息技術的不斷發展完善，機器學習也被廣泛應用于各個領域。計算機利用機器學習算法，通過模擬人類的行為不斷提高機器的工作效率。自1949年，Hebb開啟機器學習的第一步后，機器學習經歷數十年的發展不斷進步。1984年，Breiman L L[4]提出了一個著名CART算法，也就是通常所說的決策樹(回歸樹)算法，該方法通過使用簡單的規則可以在現實生活中找到更多的應用。支持向量機(SVM)方法最初由Vapnik V等[5]提出用于二值分類，其基本思想是尋找兩個并行支持向量之間具有最大裕度的最優分離超平面。2001年,Brianman L[6]提出隨機森林模型，隨機森林在大量應用中證明了其在理論和實驗上對過擬合的抵抗性。2013年,Anaissi A等[7]提出迭代隨機森林，能夠識別出特征的高階交互作用,同時能夠保證迭代隨機森林有很好的預測能力[8]。

文中利用Márcio Dias de Lima等[9]提出的新的基于F-score的特征選擇方法，將其與多個機器學習算法相結合用于多分類問題中，使用分類誤差為評價指標驗證它的魯棒性。

1 機器學習方法

1.1 決策樹算法

決策樹(CART)算法通過簡單的圖像表達，就像樹一樣，所以被稱為決策樹。一個決策樹在構建時，通過將數據劃分為具有相似值的子集來構建出一個完整的樹。決策樹上每一個非葉節點都是一個特征屬性的測試，經過每個特征屬性的測試，會產生多個分支，而每個分支就是對于特征屬性測試中某個值域的輸出子集。決策樹上每個葉子節點就是表達輸出結果的連續或者離散的數據。

1.2 支持向量機

支持向量機(SVM)方法最初由Vapnik V等[5]提出用于二值分類，與其他機器學習方法相比，它是一種很有前途的機器學習技術。SVM在統計學理論中有其基礎，該方法是基于結構風險最小化原則(SRM)。支持向量機解決了一個二次規劃問題，確保一旦得到最優解，它就是唯一(全局)解。

1.3 隨機森林

隨機森林(RF)算法將大量決策樹聚集在一起，并將它們一起用于預測最終結果。隨機森林中每棵樹都按照規則自由生長，并且不需要對決策樹進行剪枝。隨機森林作為Bagging的改進方法，擁有極強的泛化能力。

1.4 迭代隨機森林

迭代隨機森林(iRF)的基本思想是在隨機森林基礎上,通過對選定的特征進行“迭代重新賦權”，得到一個帶有特征權重的隨機森林，然后利用泛化的隨機交叉樹作用于帶有特征權重的隨機森林上，進而識別出特征的高階交互作用，同時保證迭代隨機森林也有很好的預測能力。

2 特征選擇

2.1 隨機森林計算變量重要性

R軟件中的importance()函數可以被用于隨機森林算法中，用于度量變量的重要性。Mean Decrease Accuracy(平均減少度)表示在沒有該對應特征的條件下分類準確度下降的程度，即數值越大，說明該特征在分類效果中起到的作用越大;反之數值越小，表示該特征在分類效果中起到的作用越小。

2.2 條件互信息

基于互信息的特征選擇算法是通過使用互信息尋找與類高度相關而特征之間低冗余的特征。其中，條件互信息(CMI)測量給定第三個變量時,兩個變量之間的條件依賴性[10]。

設

X=(x1,x2,…,xn),

Y=(y1,y2,…,yn),

Z=(z1,z2,…,zn)

是三組離散隨機變量。條件互信息(CMI)測量給定第三個變量時，兩個變量之間的條件依賴性。給定Z的變量X和Y的CMI定義為

I(X;Y|Z)=

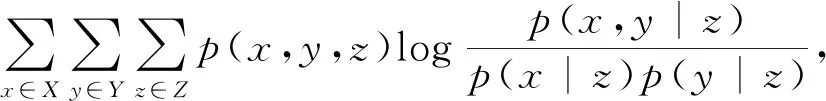
(1)

式中：I(X;Y|Z)----變量X和Y給定變量Z共享的信息量。

2.3 基于F-score的特征選擇算法

F-score作為一種簡單的方法，由Chen Y W等[1]于2006年提出，該方法用來衡量兩類數據的區別。給定特征向量xi,i=1,2,…,k，如果正負實例的數目分別為n+和n-，則第i個特征的F分數定義為

F(i)=

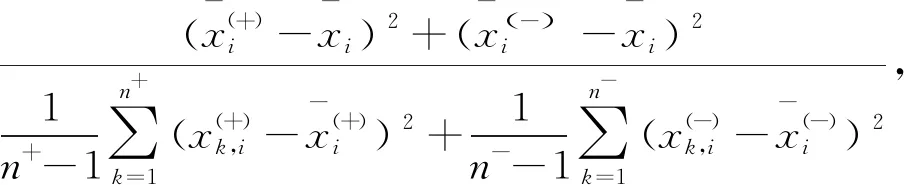
(2)

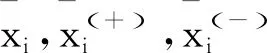
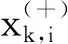
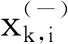
分子----正負集合之間的差異；

分母----兩個集合。

F值越大，該特征越有可能具有區別性。

F-score的一個缺點是不能揭示特征之間的相互關系。因此，Márcio Dias de Lima等[9]在此基礎上提出了一種新的變量選擇方法，分別求因變量標簽的平方距離之和除以對應實例的樣本方差，揭示了特征在不同標簽數據集下的重要性。

同樣給定特征向量xi,i=1,2,…,k，如果正負實例的數目分別為n+和n-，則以下方程定義第i個特征的正負樣本排序,

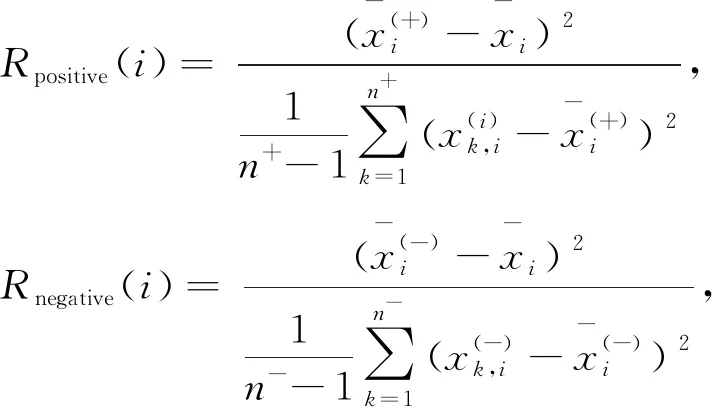
(3)

等式的分子是正負樣本第i個特征均值與總體樣本第i個特征均值之間的平方距離，而分母分別表示正負樣本的樣本方差。

特征排序(FR)由下式獲得，其中分數越高，特征越重要,

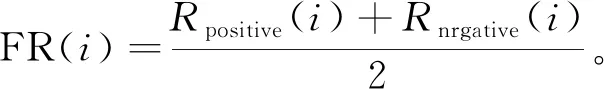
(4)

文中將該方法拓展應用于多分類問題中。給定一個特征向量xi,i=1,2,…,k，因變量xj,j∈i,j≠i，假設因變量的所有標簽用m∈R表示,則由以下方程定義第i個特征的標簽樣本排序,

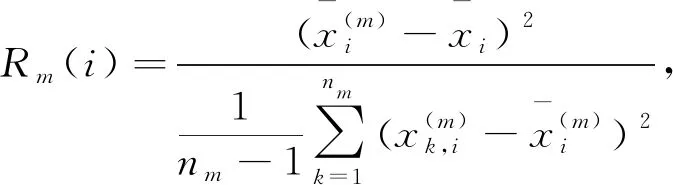
(5)

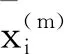
注意，上述式子的分子是第i個特征中屬于m類的均值和第i個特征總體均值之間的平方距離，分母分別匹配因變量標簽的樣本方差。

特征總體排序由下式獲得，其中分數越高，特征越重要,

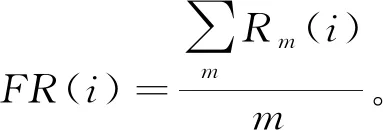
(6)

3 實證分析

3.1 數據來源

文中以UCI數據庫中的5個公開數據為例來驗證方法的可行性，為提高分類精度，在進行實驗之前對部分數據預處理，包括對Whitewine-quality數據集第3類～第5類數據劃分為bad類，第6類數據劃分為mid類，第7類～第9類數據劃分為bad類,以及對Waveform中某些無意義的變量進行刪除，最終剩余21個變量用于實驗。數據集的具體描述見表1。

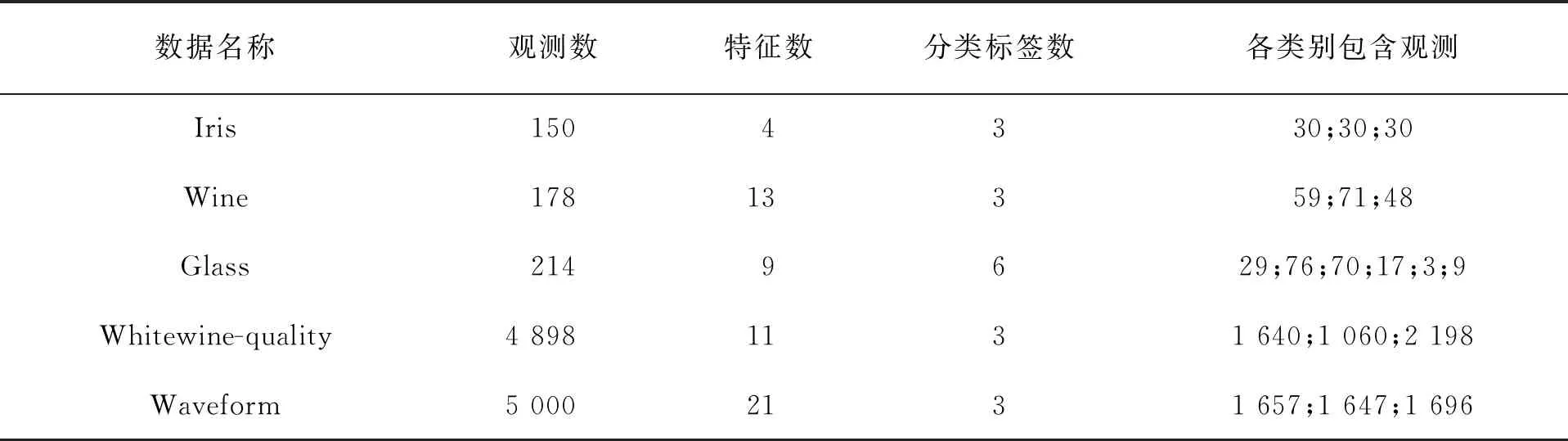
表1 數據集基本信息

3.2 交叉驗證

在建模過程中,為了避免追求高準確率而產生過擬合的情況，通常將原始數據集劃分為訓練集和測試集，從而使得模型在樣本外的數據上預測準確率也有不錯的精度。但是，劃分出的訓練集、測試集的不同會使得模型準確率產生明顯的變化。因此,為了保證輸出結果的可靠性，使用k(k=10)折交叉驗證來評估算法性能。文中為保證數據的平衡性，對每個特征的數據采取k折隨機分割，每個特征選取一個子集組成具有n個隨機特征子集的訓練集。這樣既保證了數據的平衡性，又保證了模型訓練效果的準確性。

文中所使用的十折交叉驗證數據分割方法如圖1所示(每次選擇的測試集數據由深色部分標出)。

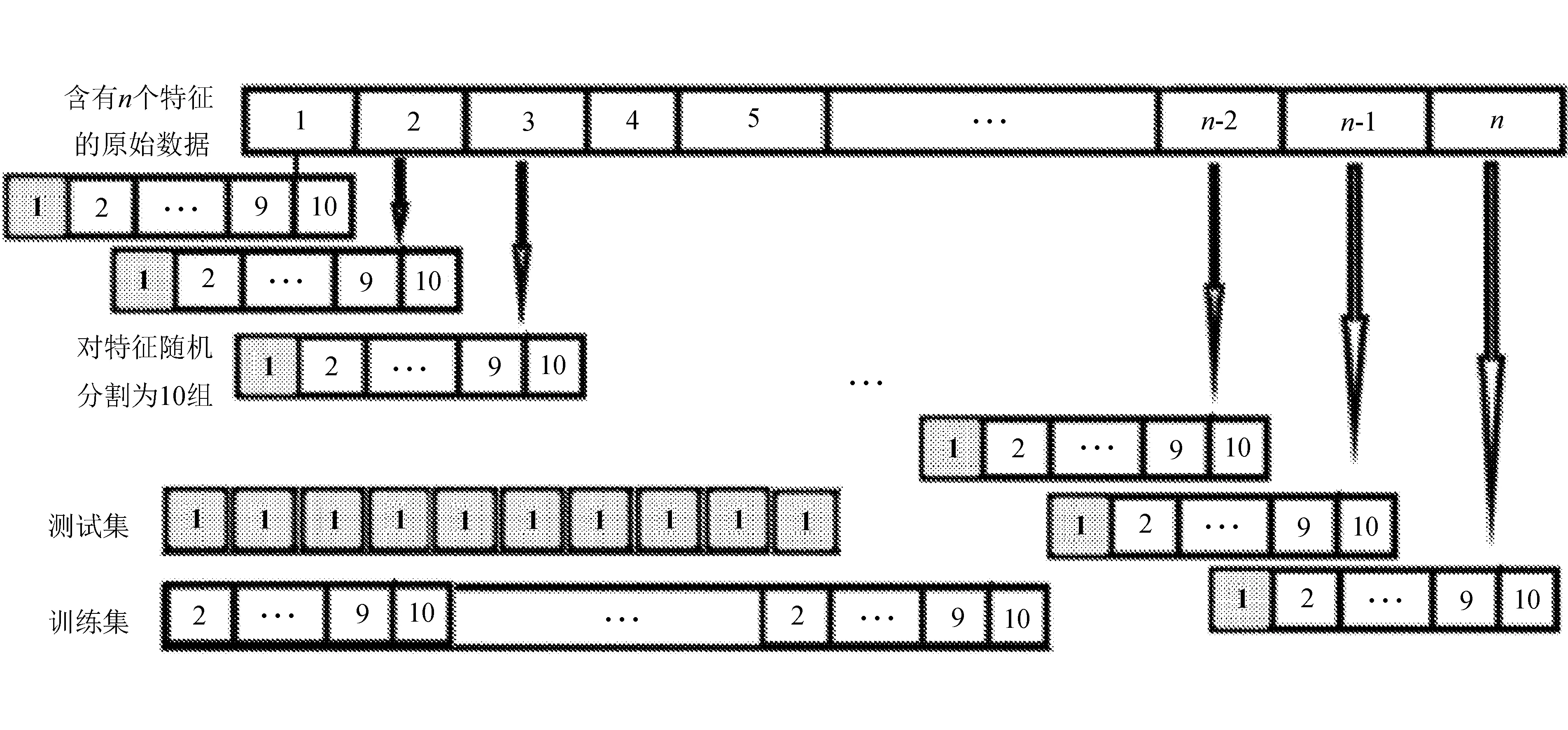
圖1 交叉驗證流程

通過十次交叉驗證所得結果的平均值報告了所提出變量選擇方法與一些機器學習算法相結合的測試精度。

用于獲得最佳精度的參數見表2(文中使用的特征選擇方法簡寫為Fs)。

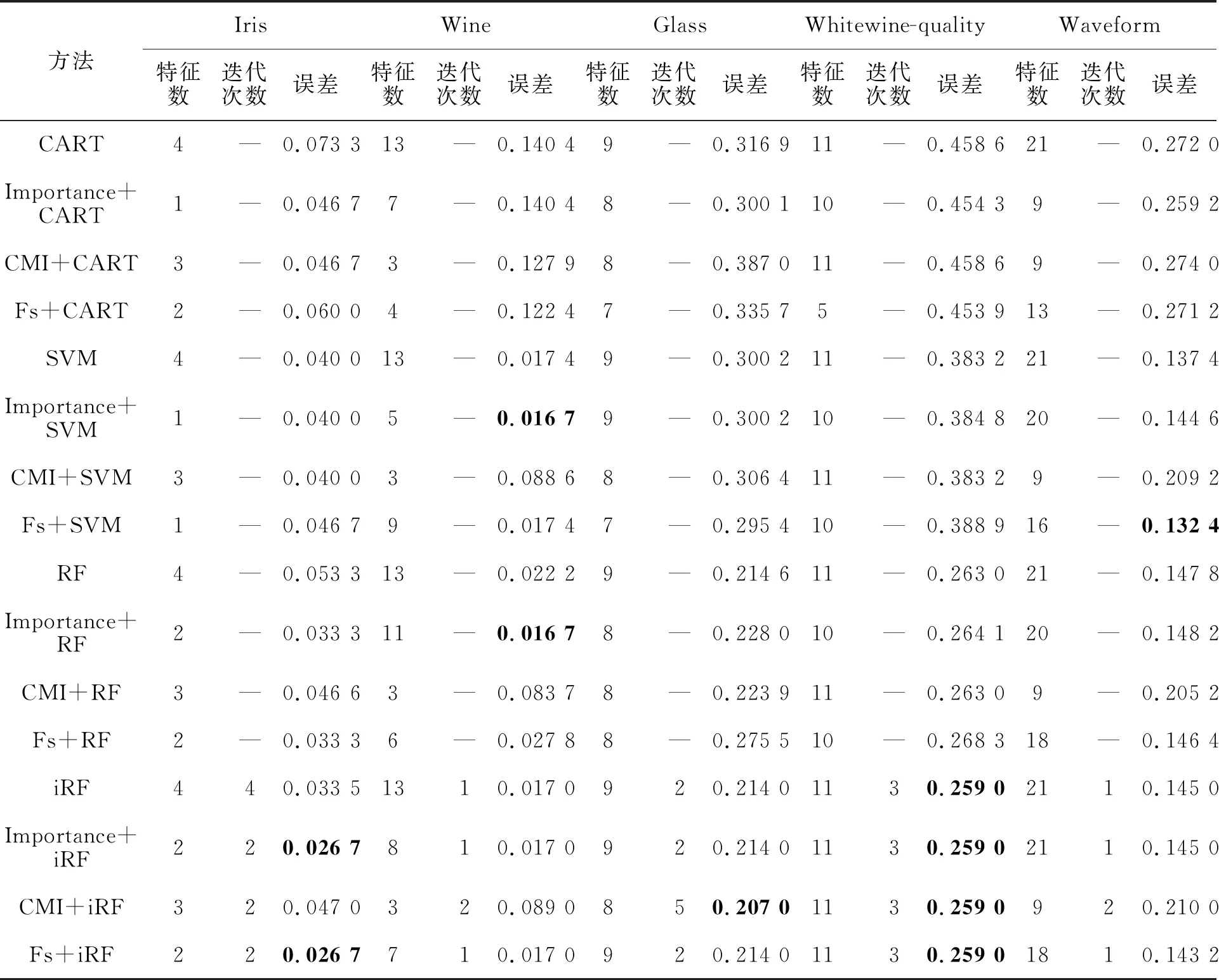
表2 模型參數配置及分類結果

從測試分類誤差角度來看，基于F-score的特征排序方法與其他機器學習方法相結合，在多分類問題中能夠在選擇較少變量的情況下達到與未進行變量選擇或與其他變量選擇方法相差無異，甚至更好。

3.3 結果分析

從表2可以得到以下分析結果：

針對Iris數據集，分類精度最好的方法為Importance+iRF和Fs+iRF，分類誤差為0.026 7，其次為Importance+RF和Fs+RF，分類誤差為0.033 3。分類最佳與次佳的誤差相差0.006 6。

針對Wine數據集，分類精度最好的方法為Importance+SVM和Importance+RF，分類誤差為0.016 7，但相比于Importance+RF方法，Importance+SVM只使用了5個變量便達到了最佳分類效果。其次為iRF、Importance+RF和Fs+iRF，分類誤差為0.017 0，但相比于其他兩種方法，Fs+iRF只使用了7個變量以及一次迭代，分類最佳與次佳的誤差相差0.000 3。

針對Glass數據集，分類精度最好的方法為CMI+iRF，誤差為0.207 0，其次為iRF、Importance+iRF和Fs+iRF，分類誤差為0.214 0，分類最佳與次佳的誤差相差0.007 0。

針對Whitewine-quality數據集，分類精度最好的方法為基于iRF的四種方法，誤差為0.259 0，其次為RF和CMI+iRF，分類誤差為0.263 0，分類最佳與次佳的誤差相差0.004 0。

針對Waveform數據集，分類精度最好的方法為Fs+SVM，誤差為0.132 4，其次為SVM方法，分類誤差為0.137 4，然而結合Fs的SVM方法只使用了16個變量,即達到了最佳效果。

通過對比不同特征選擇方法與決策樹結合的分類效果可以看到，雖然基于F-score的特征排序方法在部分數據集的表現不如使用隨機森林計算變量重要性的方法，但兩種方法的分類誤差差距不是很大。

通過對比不同特征選擇方法與SVM結合的分類效果可以看到，雖然基于F-score的特征排序方法在Iris、Wine和Whitewine-quality數據集的表現不如使用隨機森林計算變量重要性的方法和CMI方法，但針對這些數據集而言，其與最優方法之間的差距僅為0.006 7、0.000 7和0.005 7，可以說方法之間的分類誤差差距極小。換個角度可以觀察到，同樣的數據集，基于F-score的方法在Iris和Whitewine-quality數據集上所使用的特征數相對較少。可以說該方法能夠與其他方法相媲美。

通過對比不同特征選擇方法與RF結合的分類效果可以看到，基于F-score的特征排序方法在Iris和Waveform數據集上的表現優于其他方法，在 Wine、Glass和Whitewine-quality數據集上的表現雖然不是最好的，但分類誤差與其他方法相差不大。尤其在Whitewine-quality數據集，該方法與最優方法之間的差距僅為0.005 7，且使用的特征數比全變量方法要少。

通過對比不同特征選擇方法與支持向量機結合的分類效果可以看到，基于F-score的特征排序方法在Iris、Wine、Whitewine-quality和Waveform數據集的表現最佳，在Glass數據集上的表現稍遜色于條件互信息方法，但分類效果相差甚微。反觀Whitewine-quality數據集，模型的精度都是在全變量條件下達到最優，可以斷定這兩個數據集之間的特征相關系數較小，特征區分度較大。

綜上所述，與支持向量機、隨機森林和迭代隨機森林相結合的特征選擇方法都優于與決策樹相結合的方法，尤其是基于F-score和基于隨機森林計算變量重要性特征選擇方法。特征選擇與迭代隨機森林方法相結合時能夠顯著提高模型精度。同時基于F-score的特征選擇方法與機器學習方法相結合能夠達到較好的分類效果，可以在選擇少數變量的同時達到與傳統方法無異的效果，甚至是更好的分類精度。F-score通過分別計算每個特征在各個類別標簽下的分數，然后計算這些分數之間的平均值，揭示了特征之間的相互關系。相比之下，條件互信息特征選擇方法在低維小樣本數據中的表現就沒有那么出色。

4 結 語

利用Márcio Dias de Lima等[9]提出的新的基于F-score的特征選擇方法，將其與多個機器學習算法相結合用于多分類問題中，使用分類誤差作為評價指標驗證它的魯棒性。該變量選擇算法的每個特征得分都是相對于因變量的標簽分別計算的。然后，計算標簽對應分數的平均值，提供最終排名用于機器學習模型中。主要研究內容包括以下幾個方面。

1)將該方法與未進行變量選擇的模型(CART、SVM、RF、iRF)使用隨機森林importance函數所選特征相結合的機器學習模型,以及使用條件互信息(CMI)方法選特征相結合的機器學習模型相比較，驗證了該變量選擇方法在多分類問題中的有效性。

2)文中使用十折交叉驗證數據篩選框架用于模型效果對比，這樣既保證了數據的平衡性，又保證了模型訓練效果的準確性。

3)實驗結果表明，該方法能夠使用比原始數據集更少特征，并產生良好分類結果，尤其在與迭代隨機森林方法相結合的情況下，能夠顯著提高模型分類精度。

F-score方法是一種過濾器方法，能夠為每個特征分配一個得分，以構建特征排名，這種包括特征排序的方法是特別吸引人的。得分最高的特征是與因變量最密切相關的特征，反之，得分較低的特征則表示與因變量關系較小。這種過濾器方法使用與算法無關的技術比較簡單，易于運行和理解。

文中仍存在一些不足與值得改進的地方，如文中所使用的基于F-score的特征選擇方法是一種單變量特征選擇方法，需要使用窮舉方法測試每個所選擇的特征子集的分類效果，雖然難度不高，但十分費時耗力。一種自適應的特征子集選擇方法有待被開發應用于基于F-score的特征選擇算法中。其次，文中只選用了四種機器學習方法，更多的方法有待被發掘與應用。針對不同的數據特征，選擇合適的分類方法也是分類問題的關鍵。