一種動態特征匹配的部分重疊點云配準方法

杜輝，鄭長亮，苗春雨，張小孟

（1. 北京電子科技職業學院電信工程學院，北京 100176；2. 杭州安恒信息技術股份有限公司，浙江 杭州 310051）

1 引言

隨著無人機、激光雷達等技術的不斷發展，建筑物、山地、醫學、無人駕駛等場景都需要對實體進行三維重建[1-3]。三維重建研究中點的云配準與拼接技術是重點研究內容，隨著用戶對三維模型精度需求的提升，點云處理算法的可靠性要求也逐步提高。由于測量設備（如激光雷達）很難一次性完成對一個三維物體的點云數據采集，因此需要在多個角度分別采集三維物體的不同面，最后將不同角度采集的點云配準、拼接，才能得到一個完整的三維模型。綜上所述點云的配準與拼接準確率將直接決定建模的精度。高精度的三維重建算法在未來5G、6G 等通信領域具有重要的作用，如采用三維重建算法可應用于5G、6G 等研究中的建模問題[4-5]。

目前國內外學者在三維重建領域已取得豐厚的成果，如Karg 等[6]通過捕獲車輛第一、二矩陣邊界并確定第一、第二矩形是否為同一輛車的邊界，最后根據第一、二矩形和側面方向完成對車輛的三維重建。陳佳舟等[7]針對圖像點云存在噪聲干擾問題，提出一種文物三維重建點云誤差點的自動剔除方法，利用三維重投影方法計算三維點在圖像中的可見概率并剔除噪聲點，然后基于空間擴散聚類方法去除圖像冗余點，完成對文物的三維重建。Rao 等[8]提出了一種基于莫爾斯理論中的3 種臨界點的快速且精確的點云仿射不變特征檢測和匹配方法，該方法定量評估重建模型的準確性。實驗結果表明構建的三維模型精確率更高。Lan 等[9]針對前端數據關聯中幸存的異常特征匹配和閉環會導致大規模點云三維重建局部最優問題，提出了一種在出現異常值時進行穩健的后端優化概率方法。該方法利用Cauchy 分布抑制離群特征匹配，以及利用Cauchy-Uniform 混合模型抑制離群閉環約束，實驗結果表明在公共點云數據集上具有更好的重建效果。徐斌等[10]提出了殘肢表面三維重建算法，利用深度相機掃描殘肢得到點云數據，并計算該點云的特征直方圖（FPFH），然后利用采樣一致性初始配準（SAC-IA）和迭代最近點算法（ICP）完成殘肢點云的粗配準和精配準，實現殘肢表面的三維重建。張一等[11]針對傳統SLAM 算法僅能重建稀疏點云等不足，提出一種特征法視覺SLAM 逆深度濾波的三維重建方法，利用視頻序列影像實時、增量式地構建相對稠密的場景結構。丁忠軍等[12]提出一種載人潛水器的深海地貌線結構光三維重建方法，通過改進Steger 算法，利用直接標定法求得水下地形二維空間坐標，再將獲得的二維點云與多元傳感器的數據進行融合，并以姿態傳感器的數據矯正點云數據, 最終獲得地貌的三維點云數據，最后對三維點云數據進行配準。

上述方法當點云間重疊比例較大或點云間規模大小接近時能夠取得較好的三維重建效果，然而三維實體（如房子、街道等）的點云數據很難一次性采集，如果在點云數據采集過程中，激光雷達（點云采集設備）更換了位置或者角度進行連續采集時，得到的點云數據可能存在角度或大小上的變化，尤其是點云間重疊率比較低時，后續就很難進行點云的配準與拼接，從而嚴重影響建模精度。本文利用歐氏距離分割法和動態時間規整算法（DTW），能有效解決點云重疊率低和點云規模不一致的配準問題。

2 相關概述

點云是通過測量儀器（如激光掃描儀等）得到的實物外觀表面的點數據集合，由一系列二維或三維的點組成，能夠真實地反映物體表面信息。悉尼城市目標數據集[13]中的一個卡車點云如圖1所示。

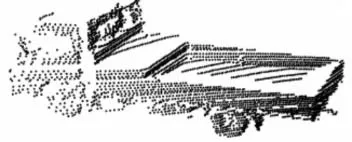
圖1 點云示意圖

要獲得一輛卡車完整的點云，需要在卡車周圍選擇若干個位置進行數據采集，然后將采集的點云幀進行組合拼接。由于相鄰位置采集的兩幀點云存在部分重疊，如果找到這些重疊的點，然后對這兩幀點云進行平移、旋轉操作，即可完成兩幀點云的拼接。點云拼接如圖2 所示，圖2 中使用兩個激光雷達掃描長方體，激光雷達1 可以掃描到的范圍為矩形RTaeh2，激光雷達2 可以掃描到的范圍為矩形RTbfgc，而矩形RTbehc可以同時被兩個激光雷達掃描，因此兩個激光雷達掃描的點云能夠覆蓋長方體的正前方和右側面，如果將兩個雷達掃描得到的點云進行配準和拼接，即可完成對長方體正前方和右側面的重建。而重建過程中最重要的就是找到這兩幀點云的重疊部分，即圖2 中RTbehc位置的點云，且重疊區域RTbehc的大小會影響點云拼接的效果。

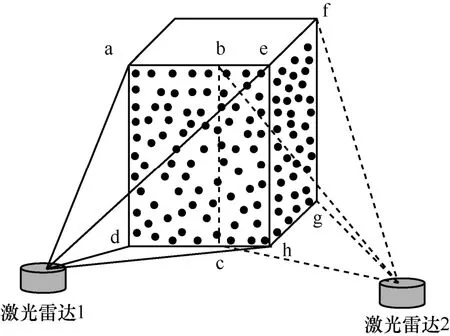
圖2 點云拼接

3 點云處理

本節主要介紹如何完成兩幀點云重疊區域的映射問題。首先介紹了基于歐氏距離的點云分割方法；然后提取子點云的特征值，最后考慮不同位置獲取的點云規模不一致，采用DTW 算法完成子點云的映射。為降低點云映射的計算復雜度，將不同激光雷達采集的點云映射到二維平面上，點云二維平面映射過程如圖3 所示，以兩個激光雷達的水平中垂線為基準，距離h處構建二維投影平面XOY。將兩個激光雷達掃描得到的點云同時映射到二維平面上，以映射后的二維點云為拼接的基礎，完成重疊點云“關鍵位置”的所搜和匹配。

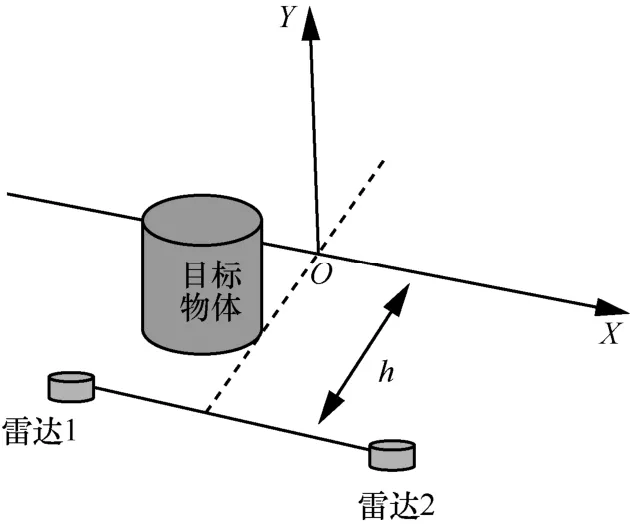
圖3 點云二維平面映射

3.1 點云分割

如果不對大面積的點云進行分割，則無法有針對性地尋找到兩幀點云的重疊區域。為有效地對點云進行劃分，采用基于歐氏距離的點云分割算法，該方法逐步掃描點云內的點，如果當前掃描點與聚類種子點之間的距離d小于設定的閾值D，則將當前掃描點聚類到該種子點所屬的類中；否則將當前掃描點設置為新的聚類種子，根據預設閾值D判斷下一個掃描點是否與新的種子點屬于同一類。重復以上步驟，直到所有的點都被聚到不同的類中。通過聚類，可以減少物體邊界點對特征點檢測的影響，同時，對于點云中不規則的離散點，往往其所在類的尺寸較小，很容易將其濾掉。點云分割流程方法見算法1，每個隊列表示分割得到的一個子點云，最終求取子點云的平均規模（即子點云內平均包含點的數量），并將子點云規模小于平均規模的子點云濾除。

算法1基于歐氏距離的點云分割算法

輸入待分割的點云O

輸出分割后的子點云Qm

（1）設置多個隊列Qm(m表示隊列數量)，預設歐氏距離閾值D；

（2）i=1；

（3）隨機搜索點云O中某個點pi作為聚類種子點，即C=pi；

（7）i=i+1；

（8）判斷點云中的點是否都加入相關隊列，如果是，結束算法，如果否，則返回步驟4。

3.2 子點云特征提取

由于激光雷達掃描物體時，物體不同表面產生的點的數量、密度和組合都是不同的，每個位置產生的點云總體上是有區別的，由于不同點云中點分布存在差異，本文假設滿足二維正態分布，且概率密度函數能夠很好地描述點云中點分布的密度、位置等差異，因此采用二維正態分布的概率密度值作為點云的特征，該特征值較傳統的均值、方差等指標具有更強的描述性。為后續進行點云的配準和拼接，需找到具有部分重疊的兩幀點云高度重合的位置（關鍵位置），反映在物體上，即不同位置的激光雷達掃描物體相同區域得到的點云。根據第2.1 節的點云分割方法，將兩幀具有重疊的點云進行分割，然后將兩幀點云分割后的子點云進行特征匹配，尋找到兩幀點云的“關鍵位置”。本節介紹一種子點云的特征提取方法，特征提取原理如圖4 所示，首先求取該子點云的重心重心坐標如式（1）所示。然后以子點云的重心為中心構建等距離g（unit）同心圓，直到最大的一個同心圓將該點云中所有的點全部囊括在內，其中，1（unit）表示20 個像素。

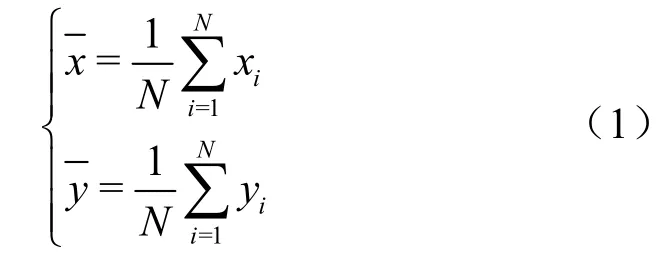
其中，xi、yi分別表示點的橫縱坐標，N表示子點云中點的數量。

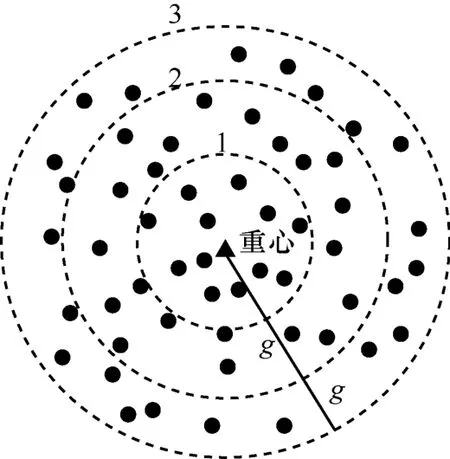
圖4 特征提取原理

假設子點云內部的點服從二維正態分布，即將每個點的坐標(xi,yi)看作二維隨機變量，那么子點云的概率密度函數如式（2）所示。

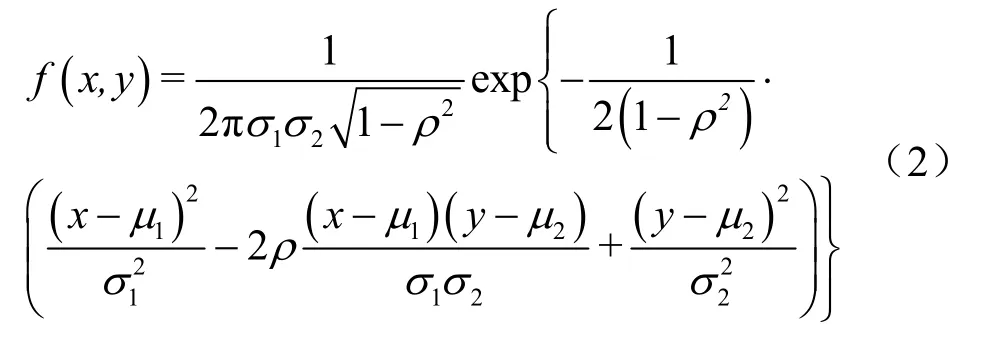
其中，μ1、μ2為x和y的均值，見式（1），σ1和σ2為x和y的方差，ρ為x和y的相關系數，絕對值小于1。

為了提高子點云的匹配準確性，使用二維正態分布模型的概率密度均值來表示子點云的特征。根據概率密度函數f(x,y)可求得點云中每個點的概率密度，求取目標范圍內所有點的概率密度值之后計算該目標范圍內點云的平均概率密度值，如式（3）所示，以平均概率密度值作為子點云的一個特征。

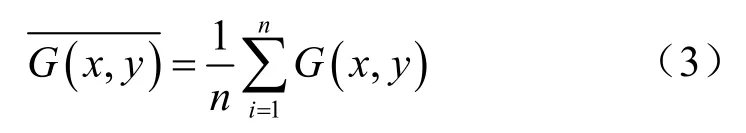
其中，G(x,y)表示點(x,y)位置的概率密度值，n表示目標范圍內點的數量。

其中，k表示點云劃分時同心圓區域的數量。

3.3 子點云映射

根據第2.1 和2.2 節的方法可以將激光雷達掃描得到的原始點云分割為若干子點云，然后求得子點云的特征序列。在進行兩幀原始點云匹配時，主要是根據特征序列實現兩幀原始點云中某些相似度較高的子點云映射。

激光掃描可類比拍照，當照相機位于不同位置拍攝同一個物體時，照片的大小也是有區別的。相同原理，激光雷達位于不同位置掃描同一個物體時，其得到物體表面的點云也存在大小的區分，本文稱為點云規模的大小不同。如果待拼接的兩幀點云存在規模上的差別，則得到的子點云特征序列長度也是不同的，不同規模子點云劃分如圖5所示，子點云p與子點云q形狀非常接近，點的分布也非常接近，但因為激光雷達所處的位置不同，導致點云規模存在差別，理論上這兩塊子點云是激光雷達位于不同位置掃描三維物體同一區域得到的數據。由于點云規模不同，而點云劃分的同心圓之間的距離相同且都為g，最終得到的子點云特征序列長度也存在差別，如子點云p的特征序列Fk長度為3，而子點云q的特征序列長度為5。針對這種情況，傳統的點云配準方法很難解決該問題。

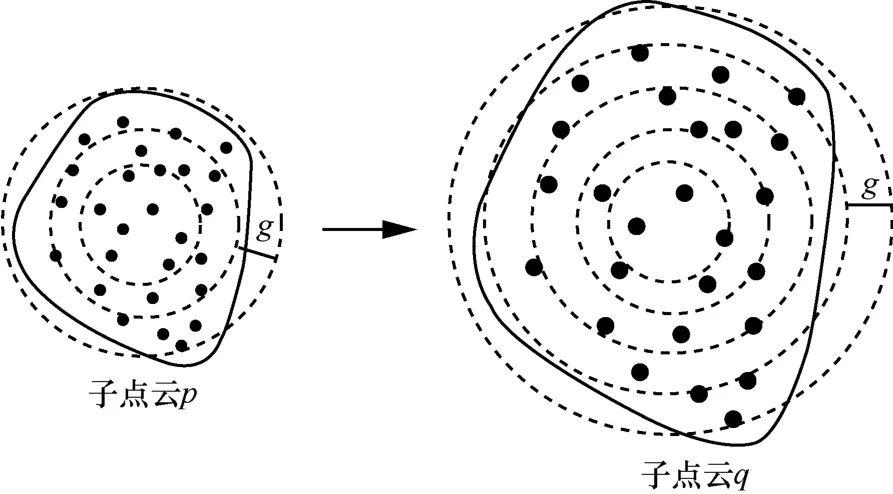
圖5 不同規模子點云劃分

為解決點云規模不一致的拼接問題，提出一種基于動態時間規劃（DTW）的點云特征序列匹配方法[14-15]。DTW 通過將特征序列進行延伸和縮短，計算兩個特征序列性之間的相似性。假設子點云p和子點云q的特征序列分別如式（5）、式（6）所示。

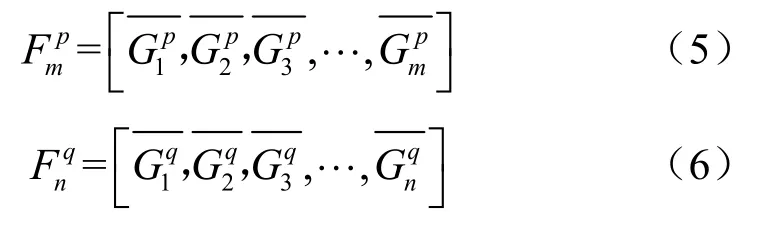
其中，m表示子點云p的特征序列長度，n表示子點云q的特征序列長度。

當m＝n時，則可以采用特征序列之間的歐氏距離衡量兩幀子點云特征序列的相似性，而當m≠n時，需要將其中一個特征序列進行線性縮/放對齊，使得兩組特征序列的長度相同，才可以進行相似性衡量。但線性縮放沒有考慮特征序列各個階段在不同情況下的長度變化，識別效果不可能最佳，更多地采用動態規劃（2ynamic programming）的方法。DTW 序列對齊原理如圖6所示，利用兩組特征序列構建一個網格矩陣，矩陣中每個元素di,j表示特征序列qnF的第i個元素與特征序列第j個元素之間的歐氏距離，每一個矩陣元素對應的下標(i,j)就表示兩組特征序列的對齊點。

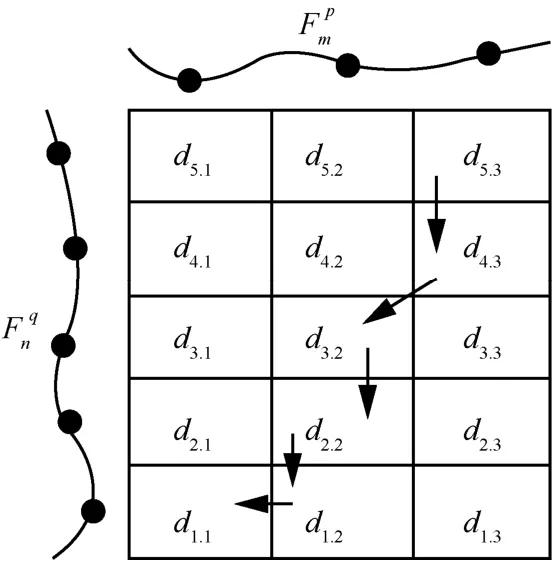
圖6 DTW 序列對齊原理

從初始點d1,1到結束點d5,3有較多條路徑，且路徑的數量隨著矩陣規模呈指數增長，如何找到一條路徑使得代價最小，最小代價的一條路徑即為兩組特征序列的最佳對齊點，最小代價函數如式（7）所示。

基于上述方法對兩組特征序列進行對齊，特征序列上的點能夠找到最佳對齊點，DTW 序列對齊原理如圖7 所示。根據對齊后的兩組特征序列之間的歐氏距離作為相似度，如式（8）所示。

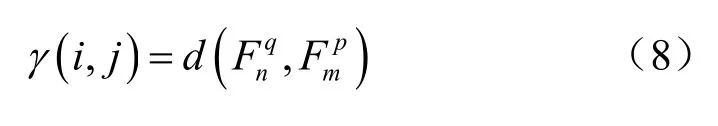
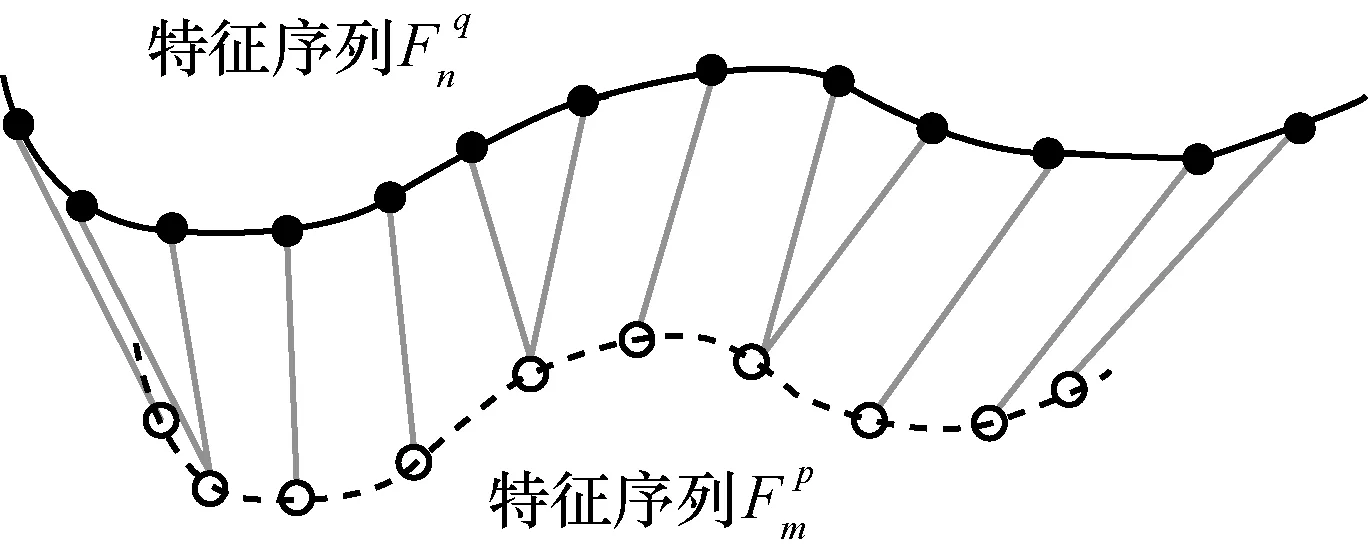
圖7 DTW 序列匹配

利用原始點云的分割、特征提取和子點云映射方法即可尋找到兩塊原始點云中相似性較高的位置，以這些位置為基準進行點云的配準將能夠有效地解決兩幀點云重疊率低以及點云規模不統一問題。本文利用上述點云映射方法所搜到兩幀原始點云中相似性最高的子點云完成映射。

4 點云配準

對兩幀點云P和Q進行分割，并獲得了互相映射的子點云p和q，然后基于子點云p、q采用ICP 算法進行配準，由于ICP 算法對點云的初始位置有較高的要求，這里需要采用SAC-IA[16-17]算法先對點云粗配準，因此要配準的兩幀點云具有較好的初始位置，再利用ICP[18-19]算法進行精配準，如式（9）所示。

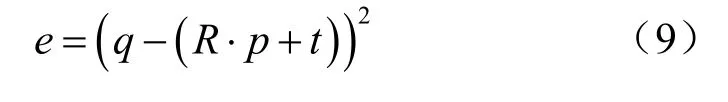
其中，R、t分別表示旋轉和平移矩陣，由SAC-IA算法和ICP 算法得到，e為優化誤差。求得的R和t再對P和Q進行配準，即可完成拼接。由于SAC-IA 算法和ICP 算法已經非常成熟，本文不再做過多的介紹。點云配準算法見算法2。

算法2原始點云配準算法

輸入點云P和Q。

輸出旋轉矩陣R，平移矩陣t。

（1）對點云P和Q分割，得到子集pi和qi；

（2）對子集分別求取二維正態分布的概率密度均值；

（3）基于DTW 算法完成子點云的映射；

（4）配準匹配的子集并獲得旋轉矩陣R，平移矩陣t，作用于P和Q；

（5）完成原始點云P和Q的配準與拼接。

算法2 介紹了點云配準算法的總體流程，該算法基于SAC-IA 算法和ICP 算法實現點云的粗配準和精配準。SAC-IA 算法與ICP 算法的總體實踐復雜度為O(sk2)，其中，s表示點云中點的數量，k表示點云被均分的份數，該值與變量g相關。而DTW 算法的實踐復雜度為O(mn)，其中，n和m分別表示兩幀點云特征向量的模。綜上所述，本文算法的總體復雜度為O(sk2)+O(mn)。

5 實驗分析

5.1 點云重疊率對配準影響

傳統的ICP 算法主要解決大規模重疊點云的配準與拼接問題，而當點云規模較小時，很難取得好的拼接效果。本文主要研究當兩幀點云具有較低重疊率和點云規模不同時的配準拼接問題。實驗采用ASL Datasets 中的“牛”點云作為實驗對象，將該點云按一定比例重疊區域進行分割，然后驗證本文提出的方法在不同重疊率情況下的配準與拼接效果，實驗中點云的歐氏距離分割閾值D=15，點云劃分同心圓之間的間隔g=3。分割示意圖如圖8 所示。

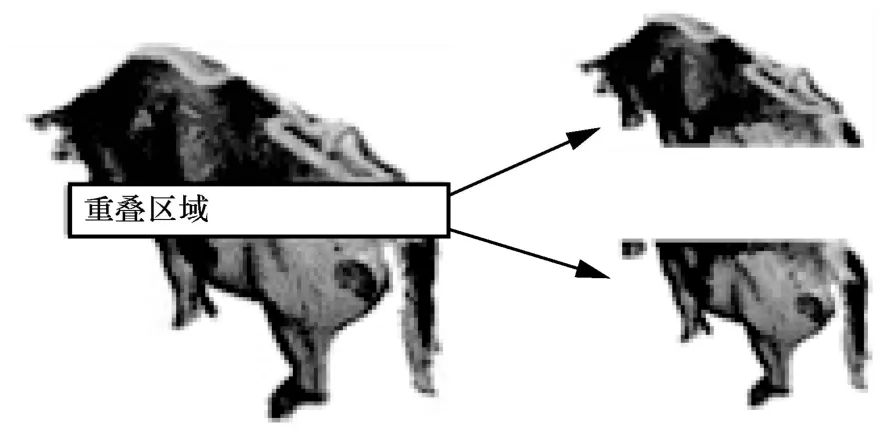
圖8 分割示意圖

首先固定一個旋轉矩陣Ri和平移矩陣ti，分別如式（10）、式（11）所示，將這兩個矩陣作用于圖8 中分割后的“牛”下部分的點云，使得兩幀點云在位置上錯開。兩幀點云位置錯開后，利用本文提出的點云配準方法（partial overlapping point clou2 registration metho2 base2 on 2ynamic feature matching，PPCR）和ICP 算法分別對兩幀點云進行配準，求取PPCR 和ICP 算法生成的旋轉矩陣Rj和平移矩陣tj，再與固定的旋轉矩陣Ri和平移矩陣ti進行對比，計算旋轉誤差和平移誤差，分別如式（12）和式（13）所示。

PPCR 算法的實驗結果如圖9 所示，表明隨著點云之間重疊率的降低，兩幀點云的拼接時的旋轉誤差ER和平移誤差Et都呈指數升高，因為重疊率越小，所以拼接算法能找到兩幀點云相似的區域的可靠性越差，導致拼接誤差較大。

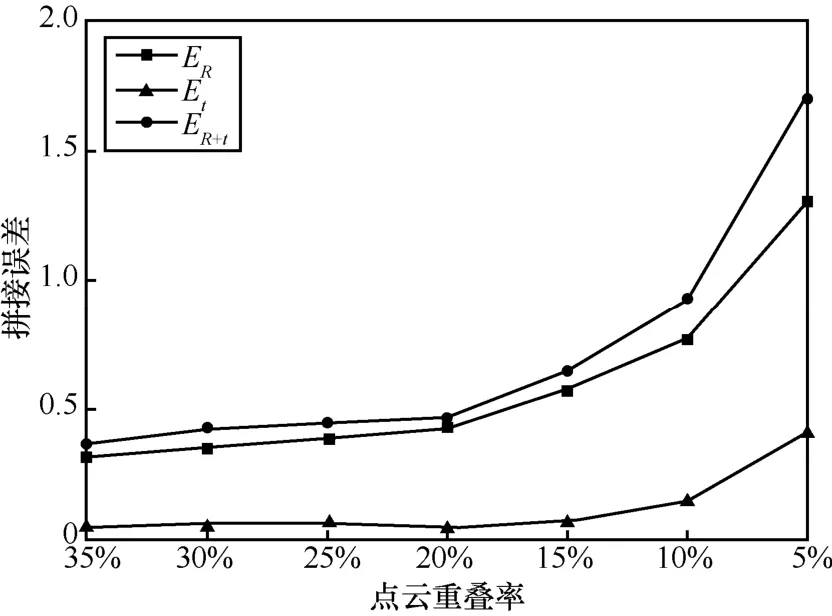
圖9 點云重疊率對PPCR 拼接效果影響

PPCR 算法與ICP 算法的對比結果如圖10 所示，ICP 在點云重疊率高于20%時有效，否則無法完成點云的拼接，且ICP 算法的拼接誤差大于本文提出的PPCR 算法，因為ICP 算法并未考慮點云重疊率時的拼接問題，其主要針對大面積重疊的點云之間的拼接，而PPCR 算法利用歐氏距離分割，提取了重疊部分點云的特征，且采用了DTW 曲線相似度動態匹配算法，即使在重疊率較低時也能夠準確地找到點云間的重疊區域，最后根據重疊區域進行拼接，因此拼接誤差較ICP 算法更低。

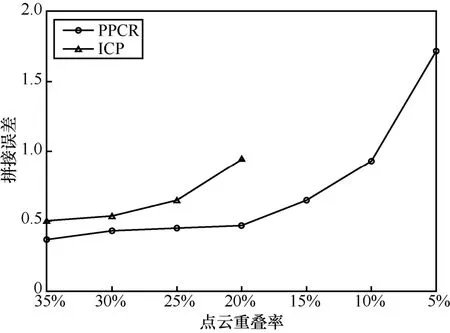
圖10 PPCR 與ICP 拼接誤差對比

單獨采用ICP 算法進行點云配準存在收斂速度慢、配準誤差大等問題。本文先采用SAC-IA算法實現點云的粗匹配，將位置錯開的點云快速實現合攏，然后采用ICP 算法進行精匹配，理論上能夠降低點云配準的時間。本實驗驗證當點云不同重疊率下，ICP 算法和PPCR 算法的配準時間，結果見表1。

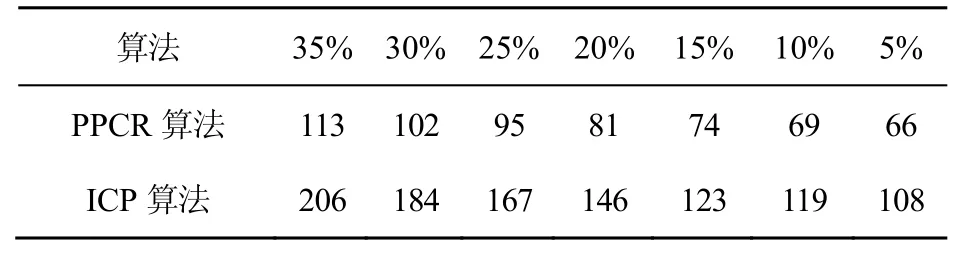
表1 時間復雜度分析（時間/s）

實驗結果表明，PPCR 算法在所有重疊率下的配準時間都低于ICP 算法，因為PPCR 算法先采用SAC-IA 算法快速將兩幀位置偏差較大的點云快速的匹配并合攏，然后采用ICP 算法進行精匹配，其中，SAC-IA 算法的效率較高。而ICP 算法在處理兩幀點云偏差較大情況時，收斂速度非常慢，因此導致配準過程所需時間較長。

5.2 噪音對點云配準影響

激光雷達發出的微波在真實環境中容易產生衍射、折射等現象，會導致采集的點云數據包含噪音，由于噪音的隨機性會影響點云配準過程中的子點云映射，因此消除噪音有利于提高點云配準的準確率。噪音在點云中一般是以少量離散點的形式存在，而本文提出的PPCR 算法在點云分割階段將點云進行聚類，因此可以根據聚類中包含點的數量來濾除噪音，當類規模小于一定值時刪除該類，濾噪對比如圖11 所示，當基于歐氏距離的點云分割得到的子點云所包含的點數量小于子點云平均包含的點數量的一半時，則刪除該子點云，實驗中點云的歐氏距離分割閾值D=15。利用第4.1 節的方法將點云分為兩部分，重疊率為20%，驗證不同程度的濾波情況下PPCR 算法拼接點云的誤差，實驗結果見表2，表2 中拼接效果一欄表示兩幀點云拼接是否有效，為1 表示有效，為0 表示無效。S 為原始點云經歐氏距離分割后得到若干子點云后，子點云平均包含點的數量，如式（14）所示。

圖11 濾噪對比

其中，n表示子點云的總數量，si表示點云i中包含點的數量。

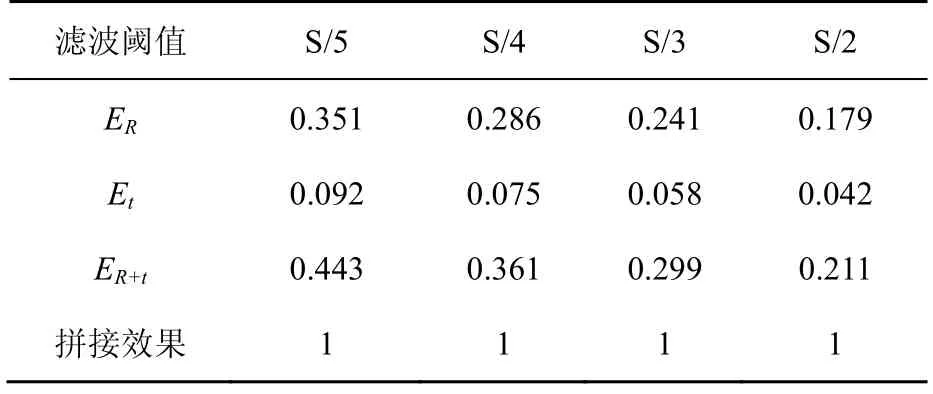
表2 濾波對點云拼接的影響

實驗中將小于濾波閾值的子點云刪除，結果見表2，隨著濾波閾值的增加，PPCR 算法的點云拼接誤差逐漸減小，總體誤差ER+t一直維持在0.5以下，因為濾波閾值越大，能夠濾除的噪聲越多，所以待拼接的兩幀子點云之間的映射更準確。

5.3 點云規模差異對子點云映射影響

PPCR 點云配準與拼接算法采用動態時間規則方法進行點云特征序列匹配，理論上能夠有效解決待拼接的兩幀點云規模不一致的映射問題。如果能夠準確地映射兩幀原始點云中相似性極高的子點云，則后續可以根據該子點云進行原始點云的拼接。以“兔子”點云為實驗對象，不同規模點云如圖12所示，為構建不同規模點云，對原始點云進行下采樣，使得下采樣后得到的點云與原始點云保持相同的結構，但點的數量不同，然后將下采樣后的點云縮小到原始點云的1/2，實驗中下采樣矩陣見表3。初始時刻兩幀點云處于相互完全重疊位置，然后利用已知的旋轉矩陣和平移矩陣作用于其中一個點云，使得兩幀點云位置錯開（見第4.1 節的旋轉與平移），以第4.1 節的配準誤差方法衡量兩幀點云的配準精度，實驗結果見表3，表3 中配準效果一欄表示兩幀點云配準是否有效，為1 表示有效，為0表示無效。實驗中的下采樣方法為僅采集采樣矩陣中心位置的元素替代原采樣矩陣中所有值。

實驗結果表明隨著下采樣矩陣的增加，配準誤差會升高，下采樣矩陣為3×3 時，配準誤差較小，僅為0.324，而下采樣矩陣為9×9 時，點云拼接誤差較大為0.979。因為下采樣矩陣越大，下采樣后得到的點云越稀疏，損失的特征越多，所以配準誤差也就越高。但利用激光雷達處于不同位置掃描同一個三維實體時，其得到的點云之間的差距不可能達到3×3 下采樣這種損失，且實驗誤差表明即使對原始點云進行下采樣操作，在丟失大部分數據時，兩幀點云的配準仍具有較高的穩健性，因此本文提出的利用DTW 算法進行子點云特征序列的匹配方法能夠有效地應對點云規模不同而導致拼接效果差的問題。

圖12 不同規模點云

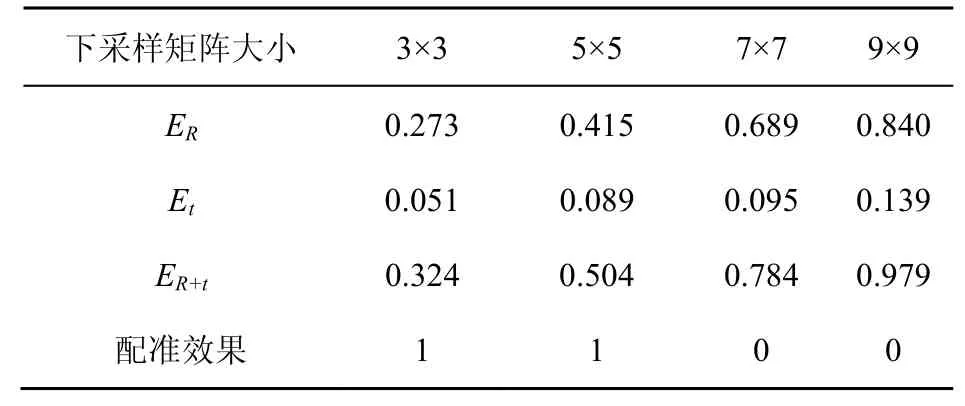
表3 不同規模點云配準誤差

5.4 分割距離g 與收斂性分析

在第2.2 節子點云特征提取階段提出采用變量g將點云進行均勻分割。當g的取值不同時，會得到長度不同的特征向量，這會影響點云的拼接效果。為驗證g在不同取值時的點云拼接誤差，實驗設定g的取值為2～10，其中兩幀點云的重疊率為20%，實驗結果見表4。

實驗結果表明隨著g的增加，點云拼接的總體誤差ER+t首先呈降低趨勢，因為g增加，提取同一幀點云的特征增加，從而降低了總體誤差。當g大于5 時，總體誤差基本呈平穩波動趨勢，因為此時點云被劃分的足夠精細，特征提取的比較全面。但g的取值并非越大越好，同時還要考慮算法的復雜度。

表4 變量g 對點云拼接的影響

6 結束語

針對目前點云配準與拼接方法較難解決部分重疊、規模不一致的點云配準與拼接問題，提出一種動態特征匹配的部分重疊點云配準方法，利用點之間的歐氏距離進行子點云的分割，然后以二維正態分布模型提取子點云的特征序列并利用DTW 算法完成特征序列的相似性匹配，接著將相似度最高的子點云進行映射，最后利用SAC-IA算法和ICP 算法完成點云的配準與拼接。實驗結果表明該方法在點云低重疊率和點云規模不一致情況下均能以較小的誤差完成配準和拼接。