淺埋地鐵隧道爆破振動速度傳播規律及預測

汪 平，吉 凌

(1.中國爆破行業協會，北京 100070；2.中國地質大學工程學院，武漢 430074)

隨著城市的快速發展以及人口的增加，地鐵隧道的建設日益增多[1-3]。城市地鐵隧道一般屬于淺埋隧道，當處于巖石地層時多采用爆破開挖方式，在施工中不可避免地要產生爆破地震效應[4-5]。當地表振動效應較大時，會對建(構)筑物造成巨大影響。因此，分析、預測隧道爆破開挖作用下地表振動特征是淺埋地鐵隧道進行安全爆破施工的前提[6-8]。

目前，關于淺埋隧道爆破開挖作用下地表振動響應特征已有相關學者作了大量研究。高文學等[7]研究表明淺埋隧道爆破開挖振動波傳播規律與其斷面尺寸、隧道埋深、開挖方法以及圍巖地質條件等有關。李勝林等[9]結合地表振動測試數據以及理論回歸分析結果預測了淺埋地表隧道爆破振動速度傳播規律。高照帥等[10]通過對現場爆破振動測試數據的分析，研究了城市淺埋地鐵隧道掘進掌子面前后相同距離處地表爆破振動特性。張繼春等[11]發現在淺埋隧道爆破開挖過程中，沿隧道軸向己開挖區的地表振動速度要大于相同爆心距下未開挖區的地表振動速度，提出了“空洞效應”現象。隨后，楊云凌[12]、喻軍等[13]、宋杰[14]研究也證實了該現象，并分析了隧道爆破開挖作用下的地表振動特性。

筆者依托武漢地鐵八號線洪山站～小洪山站區間隧道開挖工程，采用現場監測與數值模擬相結合的方法，分析了地鐵隧道爆破作用下地表爆破振動特征以及傳播規律，并對比了已開挖區域與未開挖區域的地表爆破振動特點，以便為隧道爆破振動的預測與安全控制提供依據。

1 工程概況

武漢地鐵八號線洪山站～小洪山站區間為雙線隧道，需爆破開挖區段的圍巖為Ⅲ級微風化灰巖，隧道全長326.158 m。隧道斷面形狀為曲墻仰拱形，跨度與高度分別為20.4 m與11.8 m。區段地形變化不大，地面高程為24～38 m。上覆土層自上而下依次為：雜填土、素填土、粉質黏土、黏土夾碎石、黏土、中風化灰巖、微風化灰巖等巖層，基巖埋深11.4～45.0 m不等。采用雙側壁導坑法、淺孔光面爆破開挖。為保持穩定、減小一次爆破規模，隧道共分9部分順序開挖施工。隧道斷面形狀、尺寸及施工順序如圖1所示。

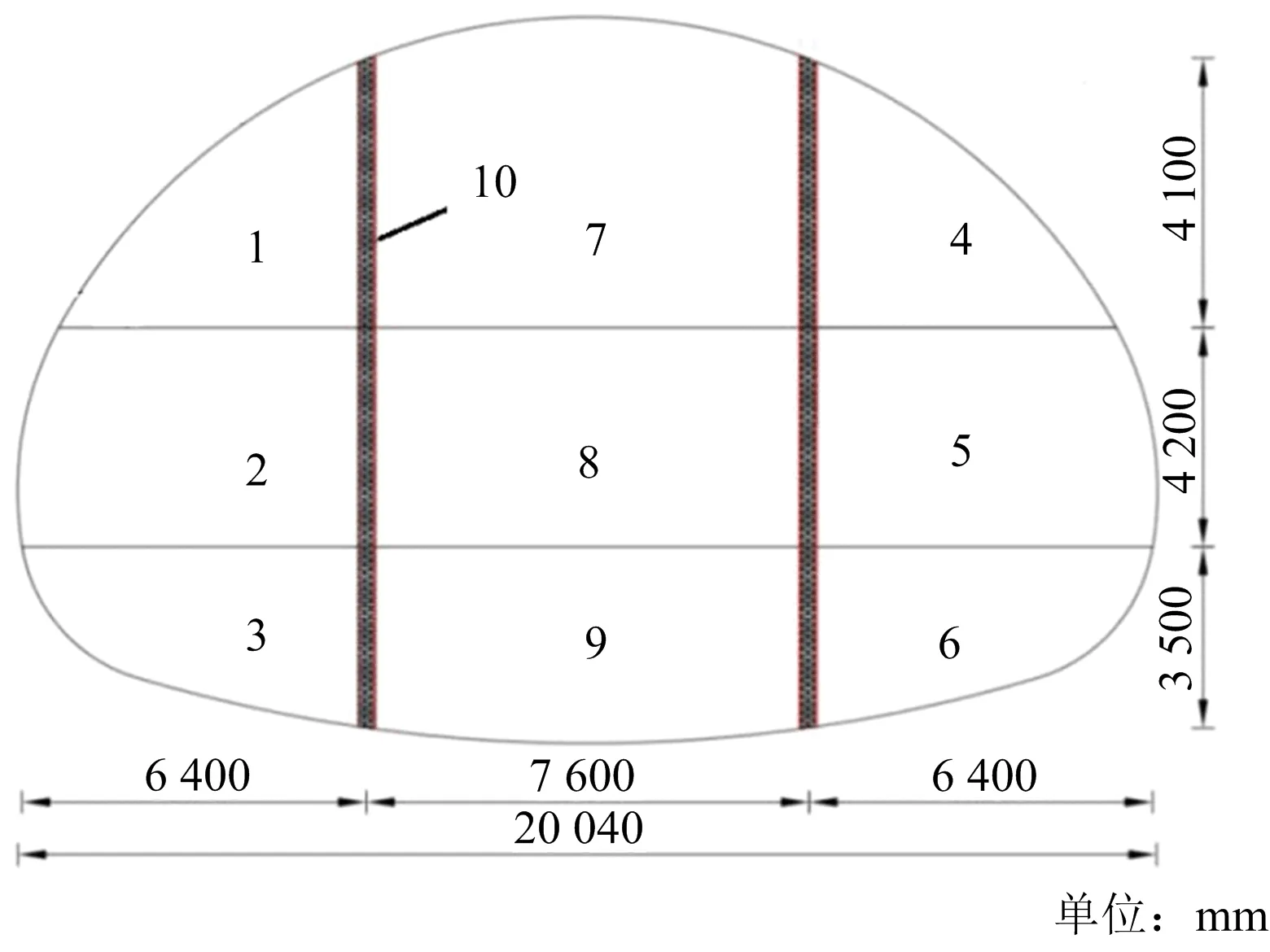
注：1～9為隧道開挖順序，10為導坑側壁。

采用對稱直孔掏槽布孔方法，掏槽孔間距為400～700 mm，周邊孔按光面爆破方式進行布孔，間距400 mm，光爆層厚500 mm，炮孔直徑40 mm，斷面炮孔布置如圖2所示。采用2#巖石乳化炸藥爆破，藥卷直徑φ32 mm，采用非電導爆管延時毫秒雷管起爆，具體爆破參數如表1所示。

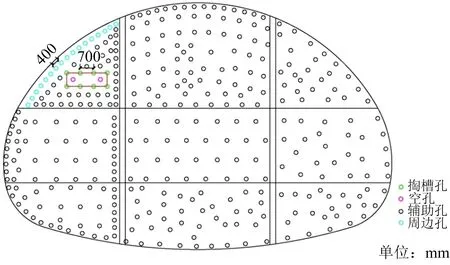
圖2 斷面炮孔布置

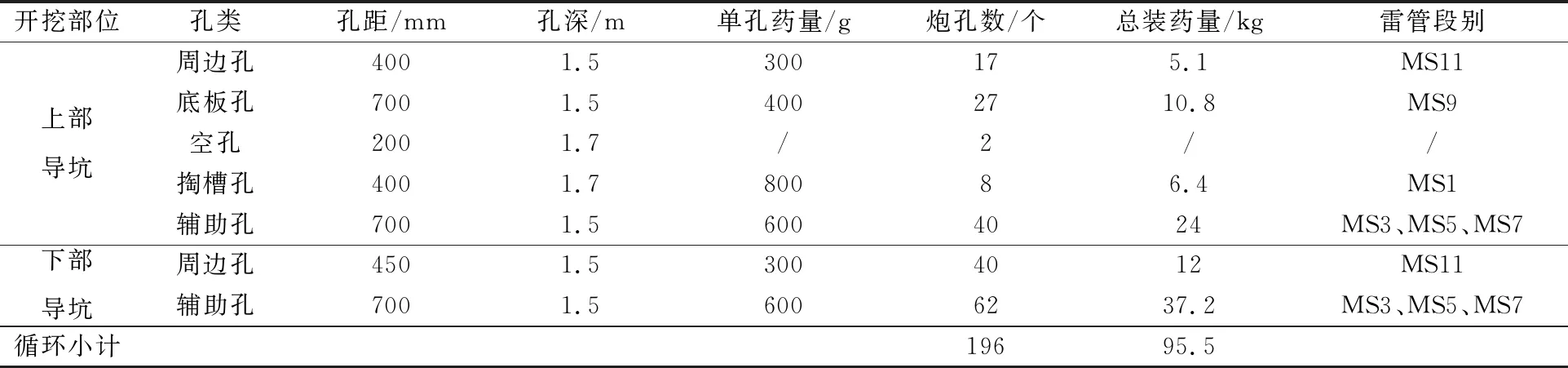
表1 隧道爆破參數

2 數值模型

2.1 模型建立

根據項目開挖工況，結合現場實際建立隧道爆破開挖模型。由于仰拱的開挖位置距離需要監測的開挖面較遠，故可在模型中將仰拱開挖假定為暫未開挖。利用ANSYS/LS-DYNA對地層及開挖隧道進行數值模擬。隧道開挖輪廓尺寸為寬20.4 m，高11.8 m。因為地下硐室開挖后圍巖應力重分布范圍為3倍硐徑，所以模型自隧道外側向外取61.2 m，向下取40.3 m。為方便建模對其進行簡化，隧道模型沿開挖設置為軸向60 m，垂向70 m，徑向140 m(見圖3)。模型的頂面(即地面)為自由面，其余5個面設置為非反射邊界。

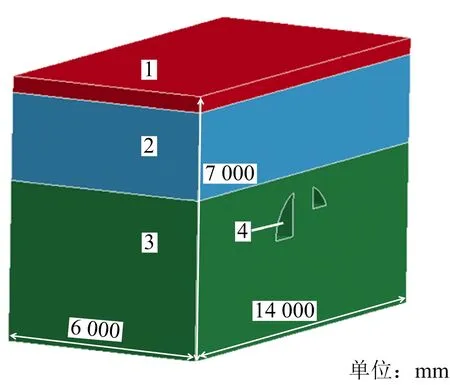
注：1-素填土；2-黏土層；3-中風化灰巖；4-開挖斷面。

2.2 材料參數

在該模型中雜填土、黏土材料使用改進的Drucker-Prager屈服面，使表面的形狀能夠被扭曲成更真實的土壤定義，中風化灰巖采用隨動硬化模型[15-16]。巖、土體的物理力學參數分別如表2與表3所示。

表2 巖體物理力學參數

表3 土體物理力學參數

由于隧道爆破開挖時，同段起爆的炮孔中掏槽孔裝藥量最大。為簡化計算，僅模擬了掏槽孔爆破。炸藥模型通過關鍵字*MAT_HIGH_EXPLOSIVE_BURN進行定義，并通過關鍵字*EOS_JWL模擬炸藥爆轟壓力，起爆點設置為炸藥底部。炸藥參數如表4所示。

表4 炸藥參數

3 結果及分析

3.1 振速波形特征

選取掌子面正上方振動速度監測點3個方向的振速波形(見圖4)進行分析，可知x(隧道徑向)、y(隧道垂直)、z(隧道軸向)方向的振動持續時間基本相同約為0.4 s，振動速度均在0.15 s左右達到峰值。3個方向的質點振動速度垂直方向最大。這是由于隧道采用雙側壁導坑法開挖，x、z方向傳播途中有臨空面，使得垂直向振速最大。

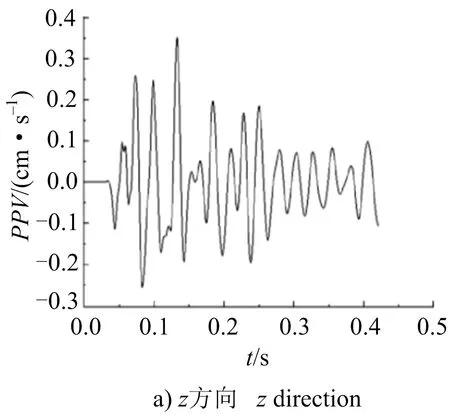
圖4 各方向峰值振速波形

3.2 振速傳播規律

1)隧道徑向地表振速預測。由地表沿隧道徑向爆破振動速度分布規律(見圖5)可以看出，地表振動速度在隧道徑向左右兩側差別較小，基本成對稱分布。隨著距掌子面距離的增加，掌子面兩側質點振動速度都呈現衰減的規律，同時由于隧道上臺階右側區域(見圖1中數字“4”所在區域)為未開挖區域，而隧道上臺階左側(見圖1中數字“1”所在區域)存在臨空面，故在距離掌子面相同距離情況下，隧道徑向已開挖區域地表振動速度峰值大于隧道徑向未開挖區域地表振動速度峰值。

薩道夫斯基公式表示了測點振速與測點距離，最大單段藥量以及爆區場地的關系，基于此關系可回歸分析出隧道徑向左側和右側方向測點爆破振動速度衰減規律，分別如式(1)、式(2)所示：

(1)

(2)

式中：Q為最大單段藥量，kg；r為測點與爆破位置水平距離，m;PPV為質點峰值振動速度，m/s。

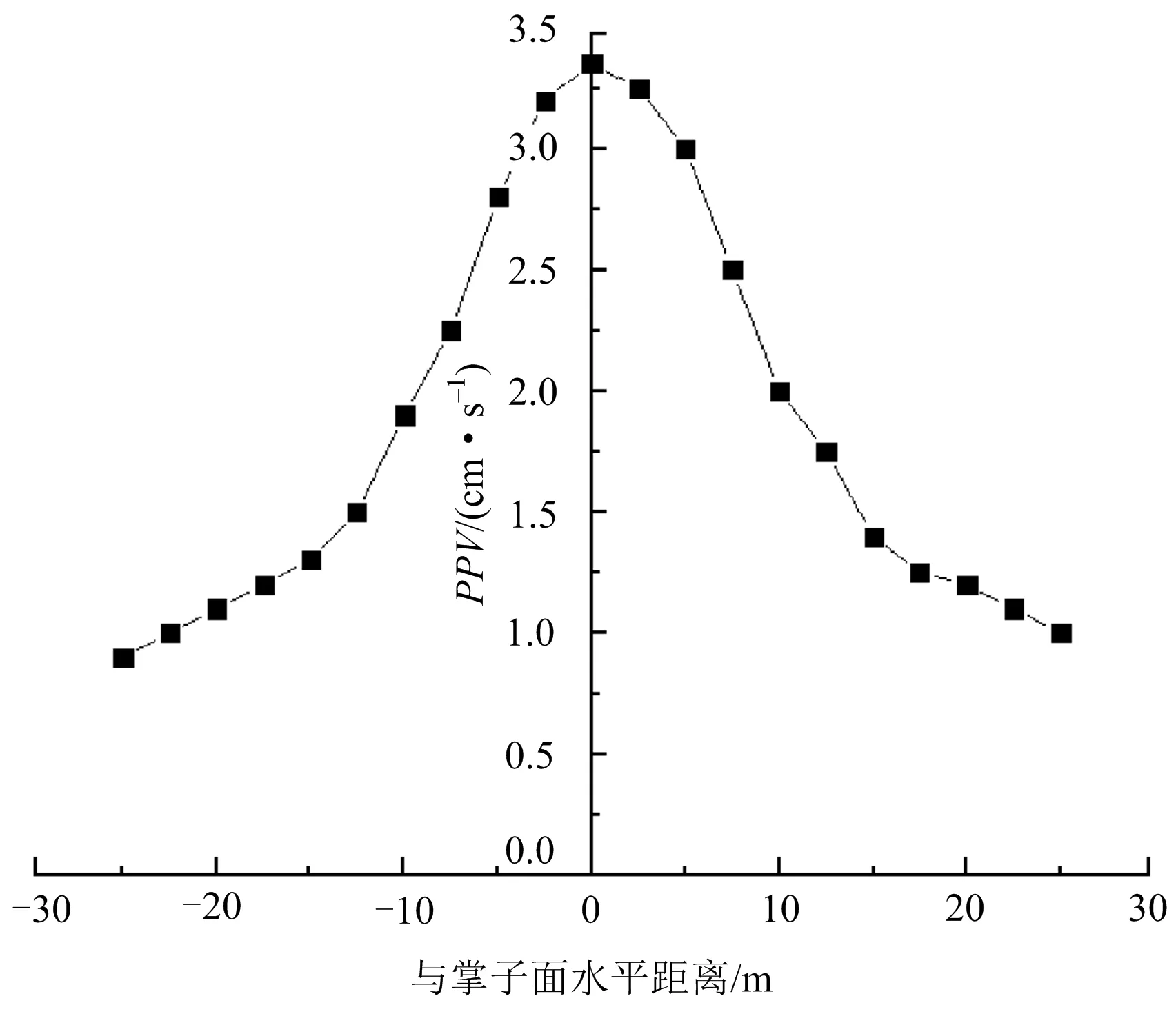
注：與掌子面距離正、負分別表示掌子面前方(未開挖區域)、掌子面后方(已開挖區域)，下同。

2)隧道軸向地表振速預測。由地表質點沿隧道開挖軸向振動分布規律(見圖6)可以看出，地表振動速度最大可以達到3.36 cm/s，掌子面前方(未開挖區域)地表振動速度隨著與掌子面距離的增加不斷衰減，掌子面后方(已開挖區域)0～10.33 m范圍內，地表振動速度隨著與掌子面的距離增加而減小，當監測點與掌子面水平距離大于10.33 m時，地表振動速度呈現出先增加后減少的趨勢。掌子面后方，大斷面左側為已開挖區域，開挖區域形成的空腔上表面為應力波的反射提供良好的自由面，入射波和反射波在地表的疊加使得監測點與掌子面水平距離大于10.33 m后，約0.6～0.7倍洞徑之間，地表振動速度產生增大的現象，此時已開挖區域對地表振動存在放大效應(空洞效應)。為了分析出隧道軸向未開挖巖體方向測點爆破振動速度衰減規律，擬合薩道夫斯基公式如式(3)所示：

(3)

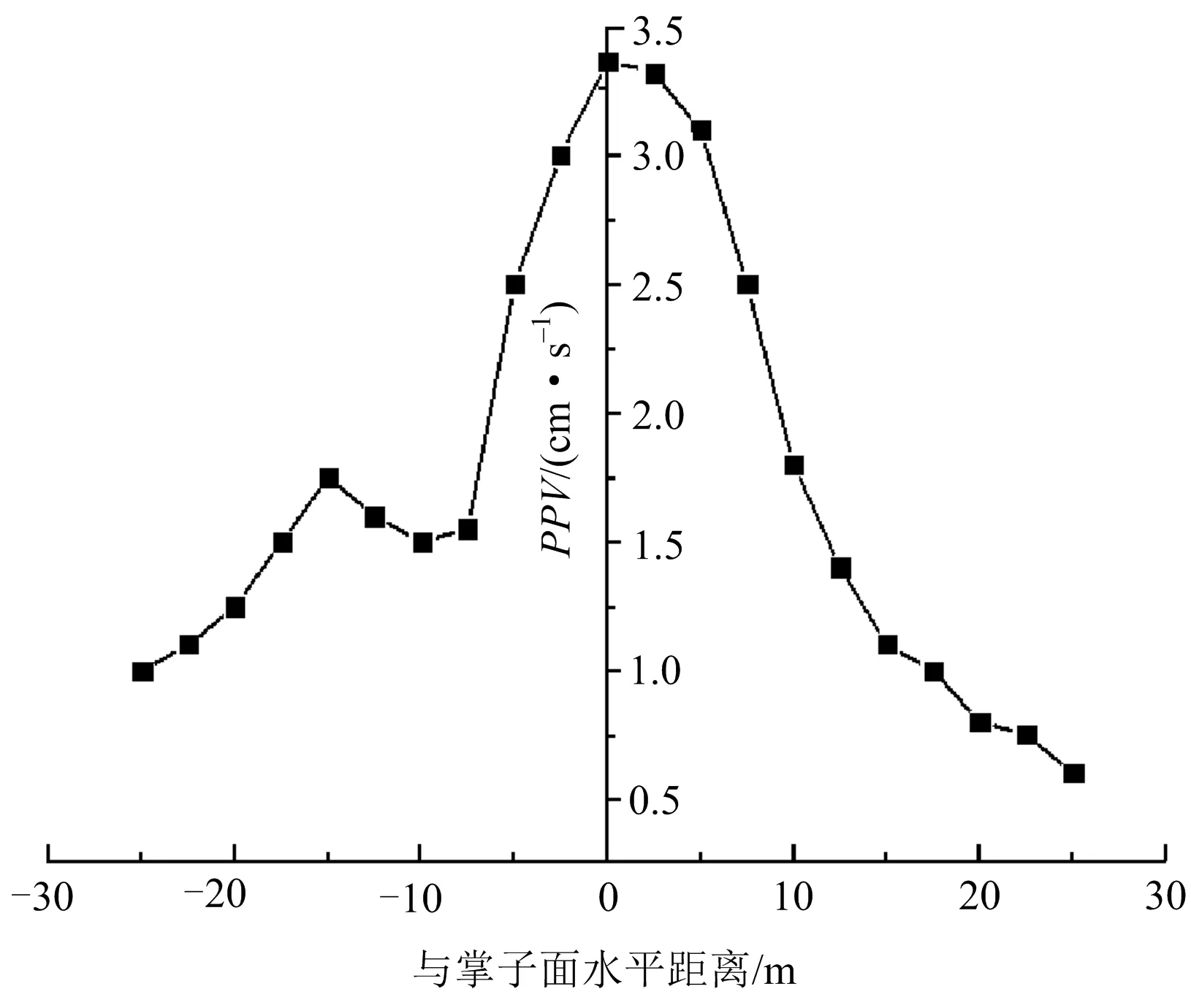
圖6 掌子面上方隧道軸向的地表質點振速分布規律

4 預測模型驗證

為研究淺埋隧道爆破振動傳播規律，現場進行5次爆破振動測試，每次爆破測試在隧道掌子面上方沿開挖軸線方向共布置5個測點，測點間距5 m。第1個測點位于掌子面正上方，其余點沿隧道開挖掌子面兩側均勻分布，測點布置如圖7所示。

將每次爆破振動測試結果平均值作為各位置爆破振動速度，提取與現場監測點相對應的數值模型上節點各方向峰值振速(見表5)可以發現，測點各方向振速最大誤差為18.2%，現場監測結果與模擬結果基本一致，驗證了模型的可靠性。從表5可以看出，y方向峰值振動速度大于x和z方向峰值振動速度，y方向爆破振動速度對地表爆破地震效應起主導作用。提取隧道掌子面正上方1#監測點實測振動波形與模擬波形(見圖8)可以看出，數值模擬結果與現場實測數據振動峰值速度大小接近、波形時間大致相同。

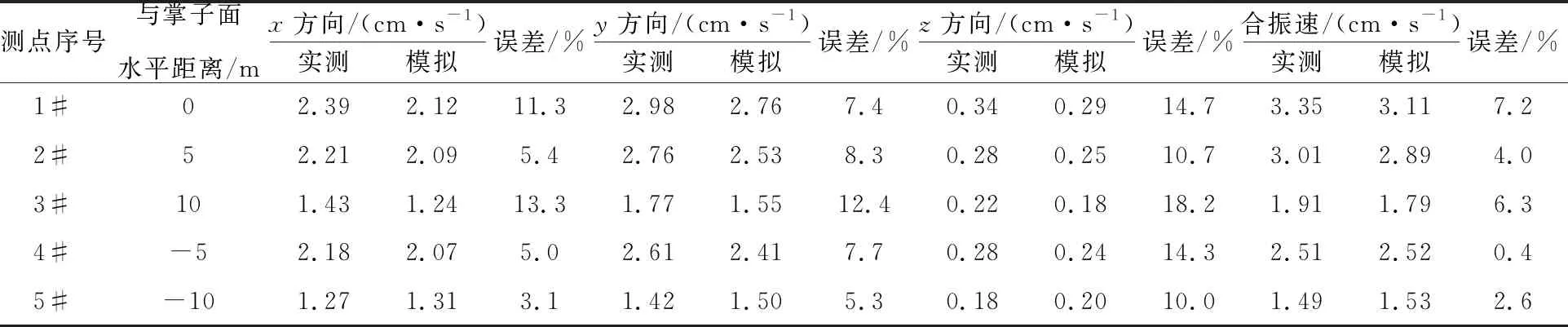
表5 實測數據與模擬結果

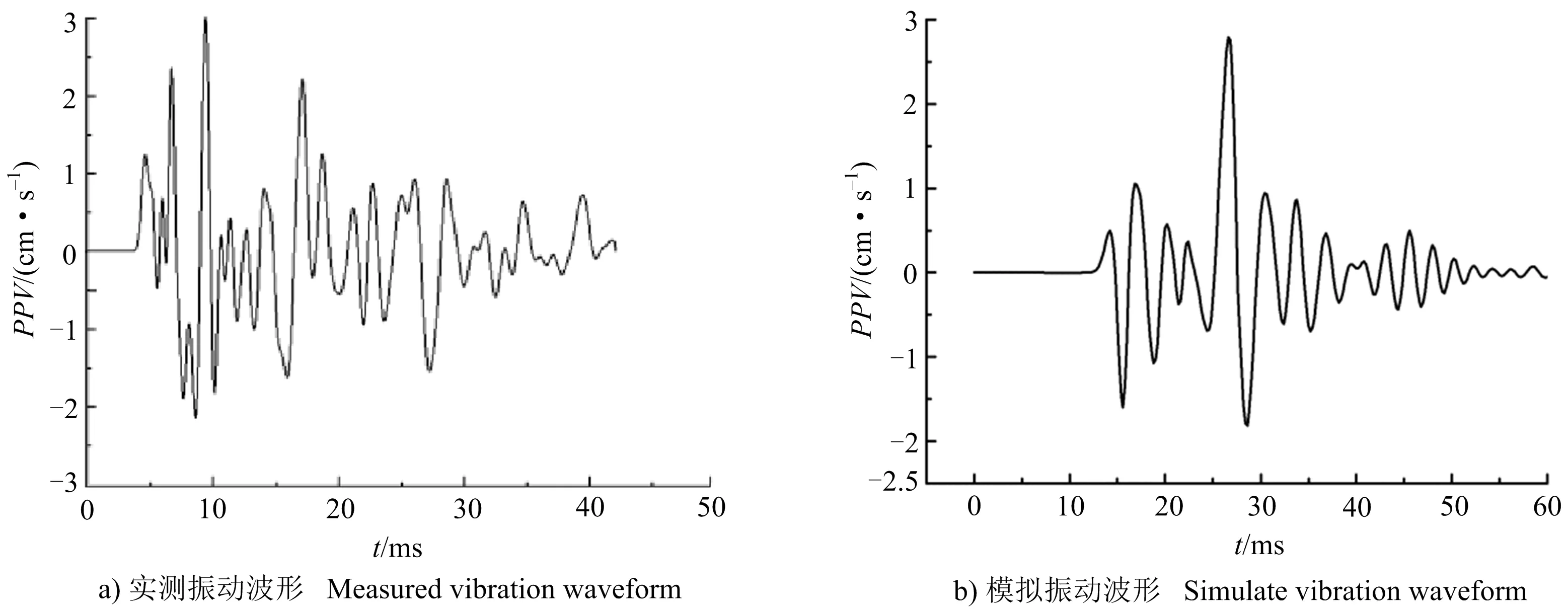
圖8 1#監測點y方向振動波形對比

5 結論

1)對淺埋地鐵隧道掌子面上方的地表進行爆破振動監測，并用數值模擬結果進行驗證，發現數值模擬結果與現場監測結果基本一致。

2)地表監測點x(隧道徑向)、y(隧道垂直方向)、z(隧道軸向)三矢量方向的振動持續時間基本相同約為0.4 s，振動速度均在0.15 s左右達到峰值振速。地鐵隧道爆破開挖作用下地表3個方向的質點振動速度為垂直方向最大。

3)沿隧道徑向方向，隨著距掌子面距離的增加，掌子面正上方左、右兩側質點振動速度都呈現衰減的規律。在距離掌子面相同距離情況下由于存在臨空面，隧道徑向已開挖區域地表的峰值振動速度大于隧道徑向未開挖區域地表的峰值振動速度。

4)沿隧道軸向方向，當地表監測點與掌子面水平距離約0.6～0.7倍洞徑后，掌子面上方沿隧道軸向方向地表振動速度產生增大的現象，此時已開挖區域對地表振動存在放大效應(空洞效應)。