砂卵石地層盾構隧道地表最大沉降量預測
韋 猛,方中楊,柴冰冰,亓金慧
(成都理工大學 地質災害防治與地質環境保護國家重點實驗室,四川 成都 610059)
0 引 言
Peck在分析了英國地鐵施工中大量的沉降數據和相應工程資料后,于1969年提出在不排水情況下隧道開挖引起的沉降槽體積應等于地層損失體積,并指出地表沉降曲線符合正態分布曲線[1-3]。在預測地表最大沉降量Smax時,沉降槽寬度i和地層損失體積V受地質特征和施工條件的影響[4]。國內外學者[5-8]認為沉降槽寬度i與隧道直徑關系很小,而與隧道埋深H、施工條件及地質特征有關;韓煊等[9]提出黏性土地面沉降槽寬度參數k=0.5;袁大軍等[10]針對南京長江隧道工程,研究了超大直徑泥水平衡盾構對土體擾動的沉降槽寬度的影響范圍;劉建航等[11]總結了上海粉細砂土隧道沉降規律,提出了“欠地層損失”的概念。對于地層損失的確定,學者們多采用傳統經驗法。韓煊等[12]研究表明,在硬黏土中用敞開式盾構開挖,地層損失率為1%~2%;魏綱[13]研究得出,在砂土地層中閉胸開挖隧道,地層損失通常小于0.5%;朱才輝等[14]研究得出,土壓式盾構隧道在軟黏土地層中損失率為1%~2%。對于一些土質較好,施工技術、施工設備相對完善的工程,經驗法具有一定參考價值和優越性,但是在施工條件、地層條件相對復雜時,經驗法計算結果與實際值往往偏差較大,并且隨著施工設備的改進、施工控制手段的逐漸加強,經驗法的弊端也隨之放大。所以周奇才等[15]用出渣量-注漿量-管片體積方法來確定地層損失。
筆者依據成都地鐵17號線白機區間地表沉降實測數據和掘進數據,對沉降槽寬度i和單位地層損失V展開研究,得到隧道埋深H=10~19 m時i與H的關系;并對周奇才[15]的單位地層損失V計算式進行了修訂,引入有效注漿率n2(n2=有效減緩地層損失的注漿量/全部注漿量)參數,提出了用已知盾構刀盤半徑、管片外徑、總注漿率、出渣量、注漿量、渣土松散系數、隧道埋深等現場數據計算地表最大沉降量的公式,并在成都地鐵17號線機終區間進行了驗證。
1 工程概況及地質特征
成都地鐵17號線白佛橋站—機投橋站(白機區間)采用盾構法施工,起止里程YDK 75+702.956~YDK 76+877.598,最小曲線半徑800 m,縱坡0~3.159~2.000~0(‰),覆土厚度10~19 m。盾構主要穿越中密砂卵石土。區間場地為第四系地層覆蓋,地表多為人工填土覆蓋,其下為沖積砂土及卵石土。盾構穿越地層及特征描述見表1。區間穿越地層見圖1。

表1 白佛橋站—機投橋站盾構穿越地層組成及特征描述

圖1 白佛橋站—機投橋站盾構區間穿越的地層
2 Peck公式介紹
1969年Peck指出了隧道開挖引起地面沉降曲線符合正態分布曲線,并給出了求解最大沉降量的Peck公式:
(1)
(2)
(3)
式中:Sx為地表沉降量,mm;x為測點距隧道中線距離,m;Smax為地表最大沉降量,mm;V為單位長度地層損失體積,m3;i為沉降槽寬度,m;H為隧道埋深,m;φ為土體內摩擦角,(°)。
3 i的確定
筆者根據成都地鐵17號線白機區間現場監測數據來分析砂卵石地層沉降槽寬度i與隧道埋深H的關系。
3.1 實測數據回歸分析
對式(1)兩邊取對數,得
(4)
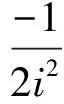
成都地鐵17號線白機左線斷面DBC-75795的實測沉降量Sx測見表2。

表2 斷面DBC-75795實測沉降量
將表2的x、Sx測轉化得到x2、lnSx算,再進行線性擬合得到回歸方程(5):
lnSx算=2.603-0.015x2
(5)
相關系數R2=0.914,表明回歸線性關系顯著。
結合式(4)、式(5)可得Smax算=-13.507 mm、i=5.844 m,即根據實測數據線性回歸后的修訂Peck式為
(6)
根據修訂Peck式(6)計算得到各點地表沉降量Sx算,結果見表2。
圖2為實測及回歸計算得到的地表沉降量曲線。
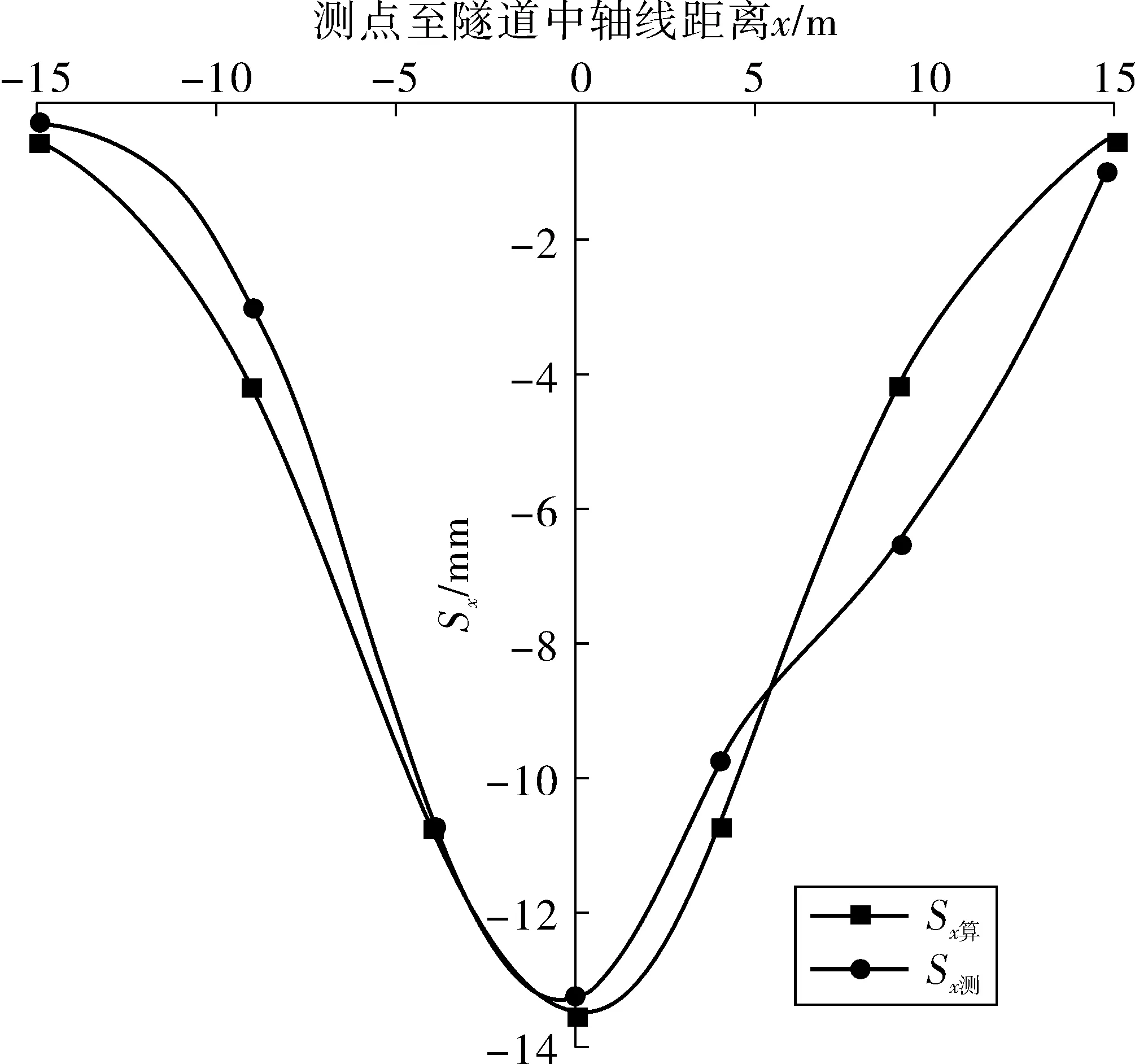
圖2 地表沉降量回歸計算值與實測值曲線
從圖2可以看出,回歸值曲線與實測值曲線最大沉降量差異不大,說明所選斷面DBC-75795沉降實測數據較為合理,且二者變化趨勢較為一致,表明用沉降量實測值線性回歸后得到的修訂Peck式(6)來求沉降槽寬度i是可行的。
3.2 沉降槽寬度i與隧道埋深H的關系
表3為根據白機區間隧道埋深H及其所對應的斷面實測值回歸后求得的i值。
表3 白佛橋站—機投橋站隧道埋深H與沉降槽寬度i統計
對表3中數據進行擬合,發現i與H的關系符合Allometricl模型(7):
i= 0.758H0.722
(7)
R2= 0.975
3.3 Allometricl模型適用性驗證
成都地鐵17號線機終區間(機頭橋站—終點接收井)與白機區間(白佛橋站—機頭橋站)相連。在機終區間左線選取5組典型斷面實測沉降量,以對Allometricl模型(7)進行驗證。各斷面隧道埋深H=9、12、14、15、16 m,斷面實測沉降量Sx測見表4。
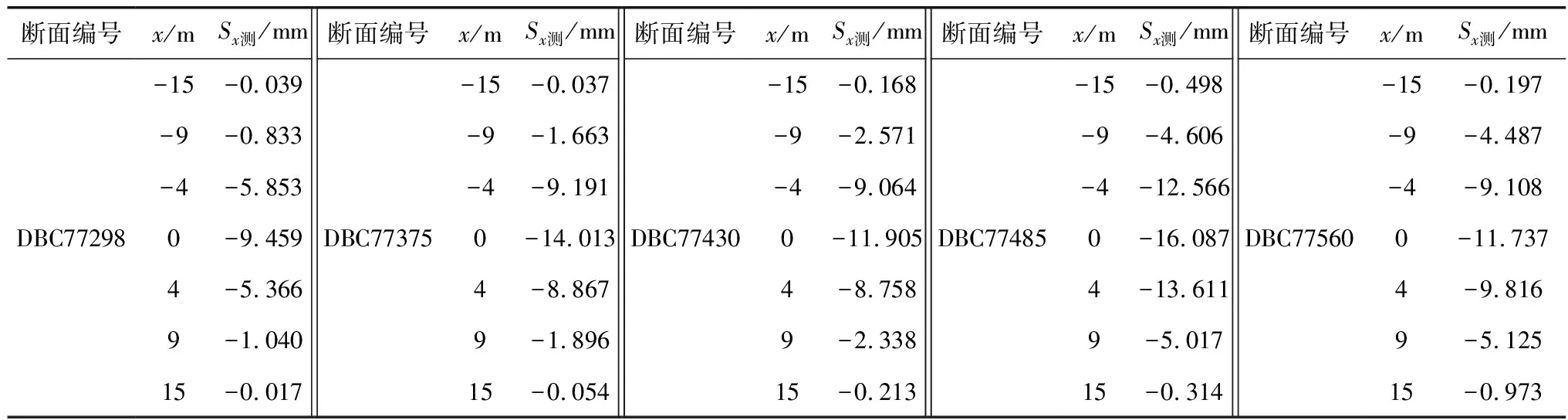
表4 機頭橋站—終點接收井左線5組斷面實測沉降量
對表4實測沉降量進行回歸分析,得到各斷面沉降量回歸式 lnSx=a+bx2,再根據式(4)得到實測回歸的沉降槽寬度i;將各斷面對應的隧道埋深H代入式(7),從而得到根據Allometricl模型(7)計算的沉降槽寬度i,結果見表5。
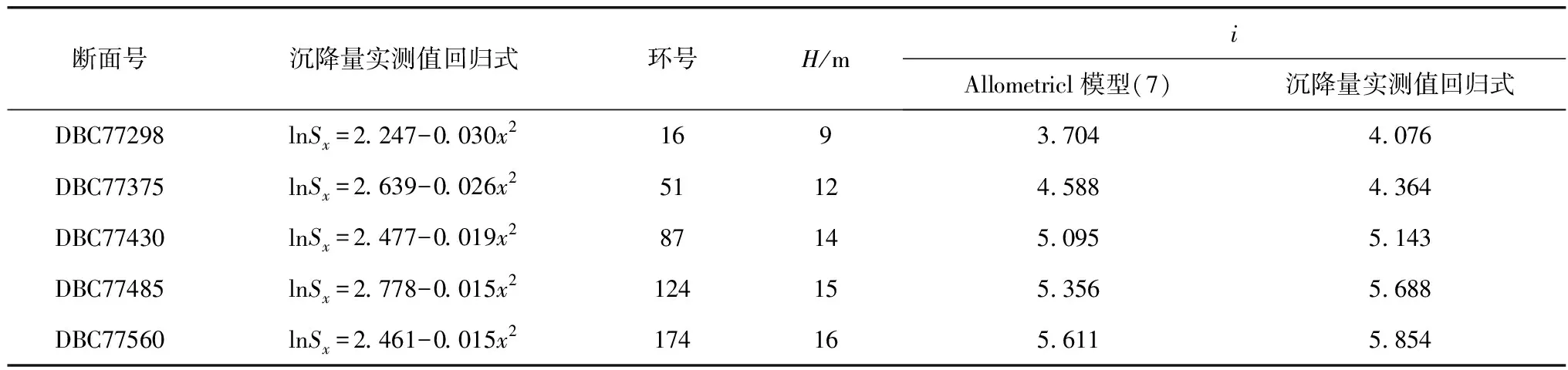
表5 實測沉降量線性回歸公式及Allometricl模型公式計算得到的沉降槽寬度i值
從表5可以看出,Allometricl模型(7)求得i與實測值回歸得到的i相差無幾,說明可以用Allometricl模型(7)來表達砂卵石地層軸線埋深10~19 m隧道沉降槽寬度i與隧道埋深H的關系。
4 V求解分析
筆者根據掘進數據對周奇才等[15]用出渣量-注漿量-管片體積方法確定的地層損失進行驗證,發現偏差很大;而從實際施工經驗及監測信息可以看出,注漿量的微弱變化會導致地表沉降量發生超過6 mm的變化。因此,筆者結合白機區間盾構掘進數據,提出用有效注漿率n2這個參數來計算防止地層沉降的有效注漿量。
單位長度地層損失體積V按式(8)計算:
(8)
式中:V1為單環出土體積,m3;n1為渣土松散系數;V2為單環注漿體積,m3;n2為有效注漿率;n為單環總注漿率(總注漿量/間隙體積);V3為單環管片外徑所占體積,m3;L為單環掘進長度,m。
在掘進中,往往要加水、泥(膨潤土)及泡沫等改良掌子面,并且開挖后,土體體積相對于開挖前有所增加。因此,在盾構完成100 m試掘進后,通過測試現場渣土來確定渣土松散系數n1的值。
向地層土體與管片之間的間隙注漿,漿液會進入周邊地層,如圖3。
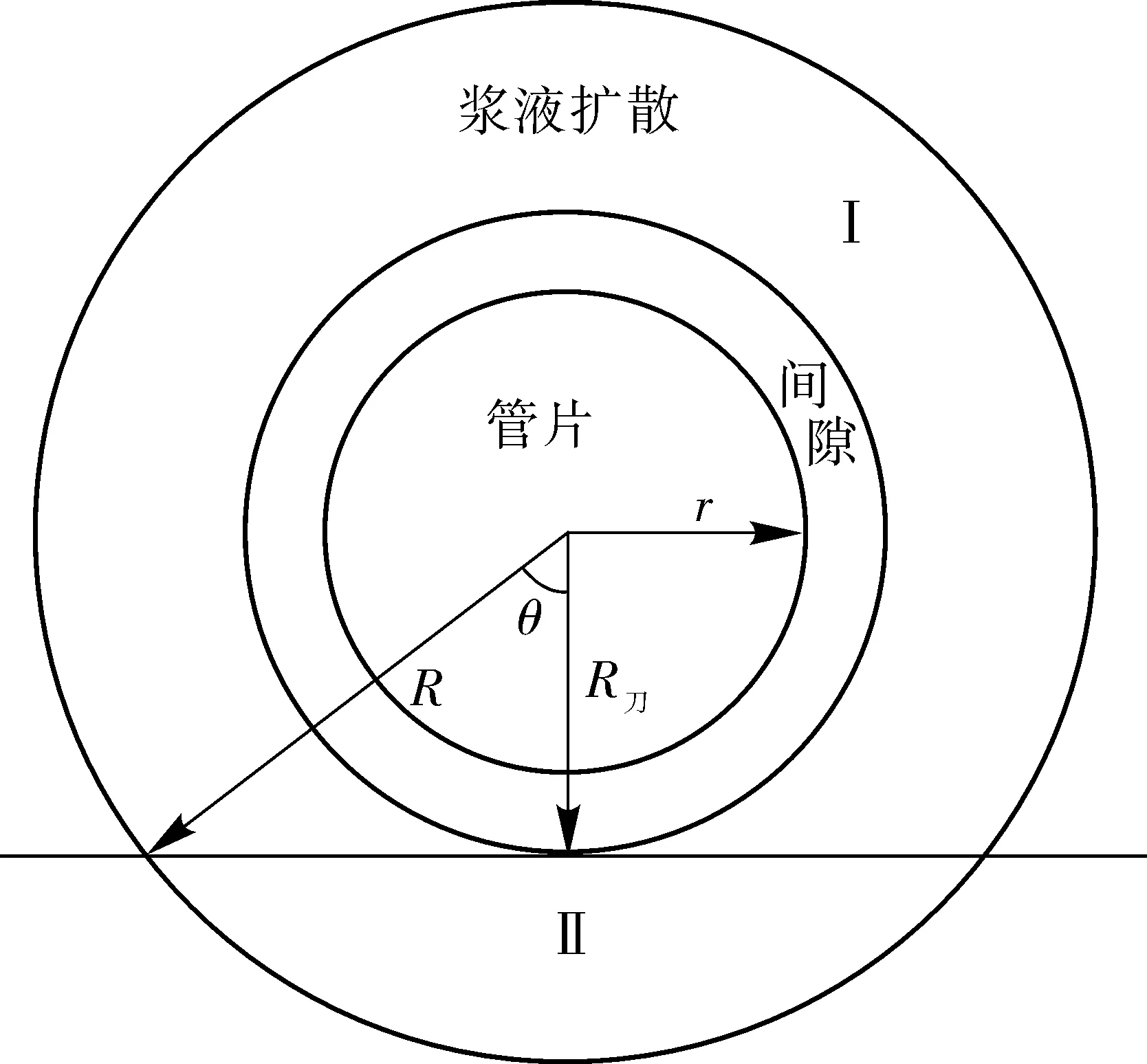
圖3 管片壁后注漿示意
為了計算有效注漿率n2的理論值,需做如下假設:①管片沒有上浮或下沉;②漿液在地層中均勻向圓周擴散;③漿液迅速在間隙中固結;④間隙漿液固結體和管片為統一剛體。
筆者認為圖4中Ⅰ部分的漿液擴散量為有效漿液擴散量Q1,則有效漿液擴散量在總漿液擴散量Q中的占比ω可按式(9)計算:
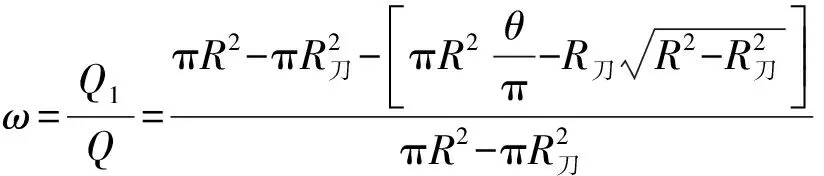
(9)
(10)
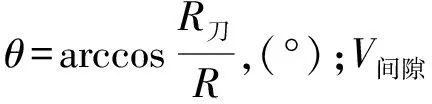
從而,有效注漿率n2為
(11)
根據盾構機和管片型號,利用盾構實測的單環出土體積V1和單環注漿體積V2,按式(12)來預測地表最大沉降量Smax:
(12)
5 地表最大沉降量Smax驗證
選擇機終左線盾構掘進狀態良好的第174環(斷面DBC77560)掘進數據來驗證最大沉降量計算式(12)。R刀=8 634 mm,r= 8 300 mm,V1=116.0 m3,V2=8.2 m3,H=16.0 m,n=1.8,L=1.5 m,n1=1.3。
分別采用筆者提出的最大沉降量計算式(12)及周奇才等[15]未考慮有效注漿層面的計算式來計算最大沉降量Smax算,并算出最大沉降量計算值與實測值Smax測誤差的絕對值|Δ|,結果見表6。
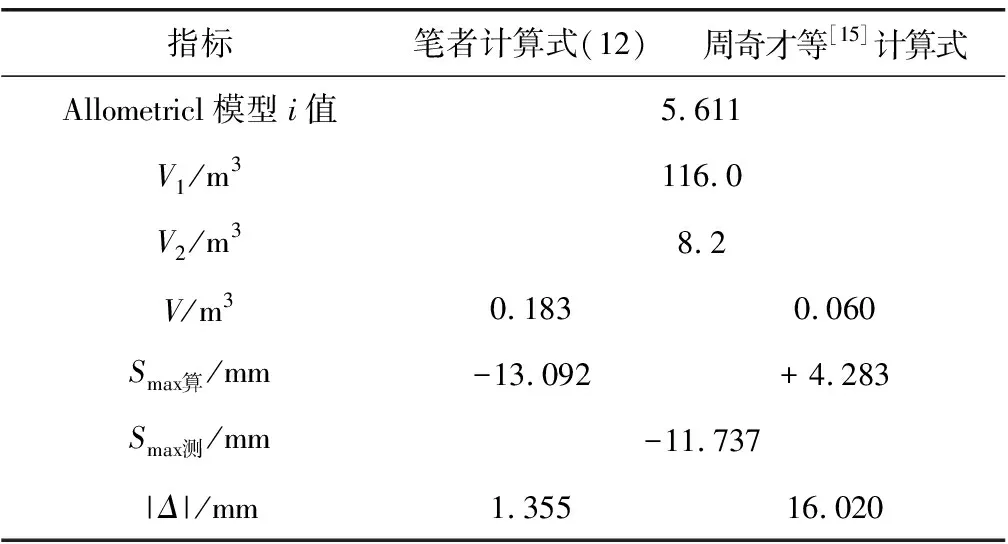
表6 計算結果匯總
從表6可以看出,用筆者提出的式(12)計算得到的最大沉降量值與實測值誤差僅為1.355 mm,遠遠小于周奇才等[15]不考慮有效注漿率時的計算結果(16.020 mm),證明筆者提出的采用沉降槽寬度i和單位地層損失V兩個參數來確定最大沉降量更合理。
6 結 論
1)用實測沉降量做回歸分析后得到的修訂Peck式來求地表沉降槽寬度i是可行的。
2)地表沉降量實測值線性回歸后得到的沉降槽寬度i與對應的隧道埋深H符合Allometricl模型關系,該模型關系可以用于埋深10~19 m砂卵石地層盾構隧道沉降槽寬度的求解。
3)為了提高單位地層損失V的求解精度,提出了有效注漿率n2參數,并給出了計算方法。
4)推導了砂卵石地層最大沉降量的計算公式,通過已知盾構刀盤半徑、管片外徑、總注漿率、出渣量、注漿量、渣土松散系數、隧道埋深等現場數據,可較為精準地得到地表最大沉降量。

