一種改進螢火蟲算法的模糊聚類方法

孟學堯，郭倩倩，郭海儒

1(河南理工大學 計算機科學與技術學院，河南 焦作 454000)2(河南理工大學 學術出版中心，河南 焦作 454000)

E-mail：guohr@hpu.edu.cn

1 引 言

螢火蟲算法(Firefly Algorithm，FA)[9]具有流程清晰、參數少、易實現等優點，在計算機網絡、圖像處理和工程設計等領域應用廣泛[10-12].Wang等[13]基于光強差異變化趨勢，提出了基于光強差的FA算法，參數設置可以隨時進行有針對性的自適應調整，平衡了探索與開發過程，有效地降低了早熟收斂的風險；崔家瑞等[14]基于螢火蟲趨光和熒光的特性提出了兩種算法，第1種基于PSO算法中的最優個體思想，提出了基于當前全局最優的螢火蟲算法(FAGO)；第2種結合貝葉斯估計法提出了基于貝葉斯估計的螢火蟲算法(FABE).除了針對FA算法自身的改進，許多研究將FA與FCM算法相結合，首先利用FA算法優化聚類中心，避免聚類算法陷入局部最優，之后利用優化好的聚類中心進行聚類操作，提升了聚類效果.林睦綱等[15]提出了一種基于FA算法的模糊聚類方法，提高了聚類精度；朱書偉等[16]提出了基于改進多目標螢火蟲算法的模糊聚類，具有較高的聚類準確率.上述FA算法結合FCM提升了聚類效果，但在初始化種群分布過程中多采用隨機的方法，限制了種群的多樣性，而且算法FAGO和FABE雖然考慮了“當前最優”和“信息素”的概念，但算法仍有陷入局部最優的可能.

鑒于此，本文首先利用切比雪夫(Chebyshev)混沌映射初始化種群分布，該映射將螢火蟲種群均勻分布到搜索空間中，生成范圍廣、分布均勻、全局搜索能力強的初始種群，可提高種群的多樣性和算法的求解精度；然后利用自適應步長因子代替固定步長因子，平衡迭代過程中算法的探索與開發能力；最后對最優種群個體所在位置進行高斯擾動突變機制，使算法能夠繼續進行搜索模式，避免陷入局部最優.將新算法運用到聚類問題中，提出一種基于改進螢火蟲算法的模糊聚類方法(a fuzzy C-means clustering based on improved firefly algorithm，IFAFCM)，該算法利用改進的FA算法搜索最優聚類中心并將其作為FCM算法的聚類初始值，可有效提高聚類性能.

2 相關工作

2.1 FCM算法

FCM是一種將樣本數據按照各自隸屬度大小進行分配的常見聚類算法.其目標函數公式如式(1)所示：

(1)

其中，n代表樣本總數，其樣本數據集X={x1，x2，…,xn}，xj={xj1，xj2，…,xjs}表示第j個樣本的s個屬性；c代表聚類質心數，V={v1，v2，…,vc}表示質心集合；元素uij表示第j個樣本隸屬于質心i的大小，m代表模糊指數，通常取常數值2；dij為每個樣本到聚類中心的歐氏距離.計算隸屬度矩陣uij和質心矩陣vi如式(2)和式(3)所示.

(2)

(3)

2.2 FA算法

作為群智能優化算法，FA在全局尋優方面比粒子群算法和遺傳算法等更有優勢[17-19].該算法通過模擬自然界中螢火蟲個體之間相互吸引和移動的過程對固定空間進行搜索和優化.螢火蟲通過自身熒光素發光使得較暗的個體向比較亮的個體移動，最終所有個體都趨近于最亮的螢火蟲，其所在的位置就是搜索空間中最優的位置.對于螢火蟲的亮度、吸引度、位置更新公式由以下定義進行描述.

定義1.兩只螢火蟲的相對熒光度，公式如式(4)所示：

I=I0e-γrij

(4)

其中，I0表示在γ=0時得到的最高熒光亮度，目標函數值越優亮度越高；γ代表光強吸收系數隨著兩只螢火蟲相隔距離越遠，體現熒光被空氣介質逐漸削弱的特性；rij表示螢火蟲i和螢火蟲j之間的距離，計算公式如式(5)所示，s表示維度.

(5)

定義2.螢火蟲的吸引度，公式如式(6)所示：

(6)

其中β0表示最大吸引度，即r=0時的吸引度，γ同上.

定義3.螢火蟲位置更新公式，公式如式(7)所示：

si(t+1)=si(t)+β(sj(t)-si(t))+α(rand-0.5)

(7)

其中，si、sj分別是螢火蟲i和j在搜索空間的位置；t表示迭代次數；β為吸引度，α為步長因子，它的取值范圍在區間[0，1]之間，這里取值為一常數；rand為隨機因子，它是在區間[0，1]上的隨機數.

3 IFAFCM算法

3.1 改進的螢火蟲算法

3.1.1 Chebyshev映射

為了驗證Chebyshev混沌映射的有效性，利用Chebyshev混沌映射方法將20個2維粒子均勻分布到用函數z形成的三維平面(如圖1所示)中，并與傳統隨機分布粒子群的三維圖(如圖2所示)進行了比較，函數z的表達式如式(8)所示：

z=3×(1-x)2×e(-(y2)-(x+1)2)-10×(x/5-x3-y5)×e(-x2-y2)-1/3×e(-(x+1)2-y2),x,y∈[-4,4]

(8)

3(1-x)2exp(-(y2)-(x+1)2)-…-1/3 exp(-(x+1)2-y2)

3(1-x)2exp(-(y2)-(x+1)2)-…-1/3 exp(-(x+1)2-y2)

通過比較圖1和圖2可以看出，Chebyshev映射方式可將螢火蟲初始種群均勻分布在搜索空間中.在相同條件下，Chebyshev映射產生的粒子能夠收集到更多的信息，有效避免了粒子群易陷入局部最優的問題.與常用的混沌映射Logistic映射[20]相比，Chebyshev映射在分布范圍與分布方式上更具優勢.

本文采用了Chebyshev映射方式生成混沌變量，公式如式(9)所示：

xn+1=cos(karccosxn),xn∈[-1,1]

(9)

其中k為階次，能夠生成不相關且帶有遍歷性質的混沌序列，Chebyshev映射螢火蟲種群數的步驟如下：

a)規定螢火蟲種群數N，在D維空間中隨機產生一個D維向量作為第1個螢火蟲個體，Y=(y1,y2，…，yd)vi∈[-1,1],i∈[1,d];

b)利用公式(9)對Y的每一維進行N-1次迭代，產生出其余的N-1個螢火蟲個體；

c)映射公式如式(10)所示，利用公式(10)將生成的N個螢火蟲個體依次映射到解搜索空間：

xid=ld+(1+yid)×(ud-ld)/2

(10)

其中，ud、ld分別為搜索空間第d維的上、下界，yid為第i個螢火蟲第d維，xid為第i個螢火蟲在搜索空間中第d維坐標值.

3.1.2 自適應步長因子

螢火蟲種群的尋優能力主要體現在個體的位置更新方法上.在公式(7)中，第1項表示螢火蟲當前所在位置；第2項表示螢火蟲的全局搜索能力；第3項表示螢火蟲的局部搜索能力，其中步長因子的調整十分關鍵.

FA算法中參數α平衡著螢火蟲種群探索與開發能力，α取值范圍為[0，1].過大或過小的隨機值都可能嚴重影響種群的搜索能力，因此設計了自適應步長機制，能夠讓種群在搜索過程中自主適時更換全局搜索與局部搜索兩種搜索方式，提高尋找最優解的能力.控制參數α的計算公式如式(11)所示：

αt+1=αtδ, 0.5<δ<1

(11)

其中δ代表冷卻系數.在迭代初期，為步長因子α賦予一個較大的取值，保證前期有較好的全局尋優能力；之后在一次次的迭代過程中α值逐漸減小，確保了較好的局部搜索能力.通過α值的調節，能夠更好地平衡螢火蟲算法的全局搜索能力和局部搜索能力.

3.1.3 高斯擾動機制

由于FA算法在陷入局部最優的狀態時，算法本身自帶的隨機擾動策略在多維條件下無法跳出局部最優位置，因此一種適應性更強的擾動機制被需要.高斯擾動是一種針對局部最優問題常用的擾動策略，它對每次迭代后獲得的最優個體進行高斯擾動得到新的最優個體，直到高斯擾動無法獲得新的最優個體，說明算法已經達到了全局最優.

高斯擾動的基本原理是為每次迭代過程中的最優個體的位置向量添加一個小幅度的隨機向量，并且這個向量要符合正態分布.其公式如式(12)所示：

(12)

在算法每一次迭代過程中，Gbest對應當代最優位置，將其進行高斯擾動，其公式如式(13)所示：

NGbest=Gbest(1+N(0,1))

(13)

向量NGbest表示高斯擾動后形成的新位置向量，之后對全局最優位置進行更新，其更新公式如式(14)所示：

(14)

綜上所述，改進的螢火蟲算法步驟如圖3所示.

圖3 改進螢火蟲算法流程圖Fig.3 Flow chart of improved firefly algorithm

3.1.4 所提算法驗證

針對所提算法的有效性進行驗證，實驗中用了f(1)https://archive.ics.uci.edu/ml/index.php、f2和f3這3個測試函數在30維的基礎上測試所提算法的求解精度和穩定性，具體描述信息如表1所示.其中f1和f2屬于單峰函

表1 測試函數Table 1 Test function

數，目的是為了測試算法的求解精度，f3屬于多峰函數，目的是為了測試算法尋找最優點的能力.將所提算法在3種測試函數中將30個粒子分別運行20次，每輪迭代500次，求出它的平均值與標準差，之后與其余5種算法FA[14]、FAGO[14]、FABE[14]、PSO[19]和GA[19]進行對比，其對比結果如表2所示，證明了所提算法在6種算法中無論是單峰函數的求解精度還是多峰函數的尋最值點都具有良好的競爭力，在與模糊聚類進行結合時能夠在一定程度上解決FCM算法對初始聚類中心的敏感和易陷入局部最優的問題，能夠為改進的模糊聚類算法聚類取得的成果提供充實的依據.

3.2 IFAFCM算法

結合IFA算法較強的全局尋優能力和尋優精度與FCM算法較強的局部搜索能力，設計了一種改進螢火蟲算法的模糊聚類算法IFAFCM.IFAFCM聚類方法在尋優方面有明顯改善，聚類性能和抗噪能力有明顯的優勢.

表2 6種算法在3種測試函數下的結果比較Table 2 Comparison of the results of six algorithms under three test functions

在IFAFCM算法中，將模糊聚類的目標函數代替螢火蟲的亮度，目標函數值越小說明螢火蟲的位置越好，亮度越高，所以目標函數與個體亮度呈反比.亮度公式如式(15)所示：

(15)

在該算法中每一只螢火蟲都可看作是一個聚類中心，其位置向量為V=(v1,v2,…,vc)，其中vi為第i個聚類中心.螢火蟲各個生物特性在聚類過程中的對應作用關系如表3所示.

表3 螢火蟲生物特性對應關系Table 3 Correspondence of firefly biological characteristics

由于利用IFA算法找到的最優聚類中心可能是近似解，因此需要將最優聚類中心作為傳統FCM算法的初始聚類中心進行進一步的優化.基于IFA算法的模糊聚類方法的流程圖如圖4所示.

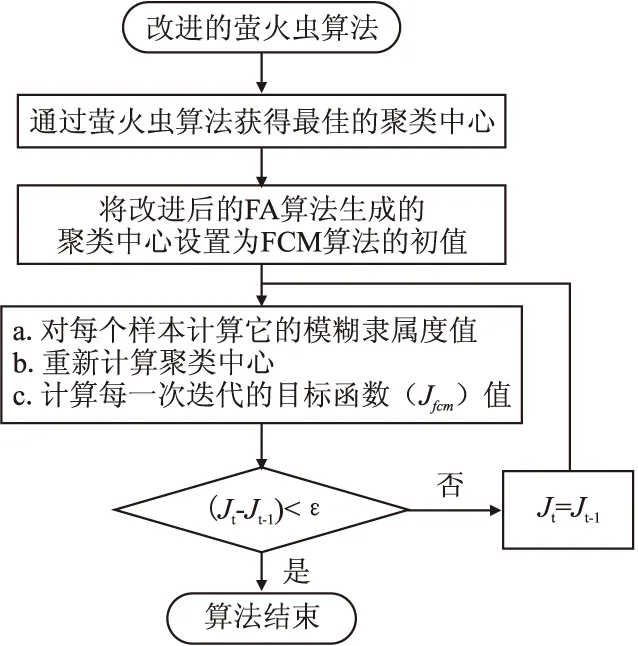
圖4 IFA算法的模糊聚類方法流程圖Fig.4 Flow chart of fuzzy clustering method with improved firefly algorithm

IFAFCM算法步驟如下所示：

輸入：IFAFCM算法的控制參數和聚類評價指標.

輸出：聚類準確率(ACC)和標準化互信息(NMI).

1.初始化種群各個參數，如N、β0、γ、α、δ、c、maxT和閾值ε；利用Chebyshev混沌映射在搜索空間均勻分布種群V1，V2，… ，VN；計算種群中每只螢火蟲的亮度I(Vi).

2.比較各個螢火蟲個體的亮度I(Vi)，利用公式(7)和公式(11)進行螢火蟲的位置更新.

3.利用公式(6)計算螢火蟲之間的吸引度βij，用公式(2)計算Ui，用公式(15)更新由于位置改變而改變的亮度I(Vi).

4.對螢火蟲進行排序，找出當前最優個體，記錄其位置并利用公式(13)和公式(14)進行高斯擾動進行位置更新；

5.判斷算法是否達到終止條件(最大迭代次數或收斂閾值)，若是則輸出全局最優個體，若否則轉到步驟2.

6.將找到的最優點作為FCM算法的初始值進行聚類，輸出ACC和NMI值.

4 實驗結果與分析

4.1 實驗操作平臺

本實驗的程序運行環境為：處理器CPU英特爾 Core i7-8750H，主頻2.20GHz六核，內存8GB，操作系統：Windows 10 64位，集成開發環境為Matlab 2014a.

4.2 實驗數據集

在實驗過程中，采用了UCI數據庫1中常用的4個數據集：鳶尾花(Iris)數據集、大腸桿菌(Ecoli)數據集、紅酒(Wine)數據集和玻璃(Glass)數據集，各數據集的詳細信息如表4所示.另外，在聚類過程中為了避免由于特征數值之間差異太大對聚類結果造成影響，對數據集的數值進行歸一化處理，使得特征數值處在[0，1]之間.

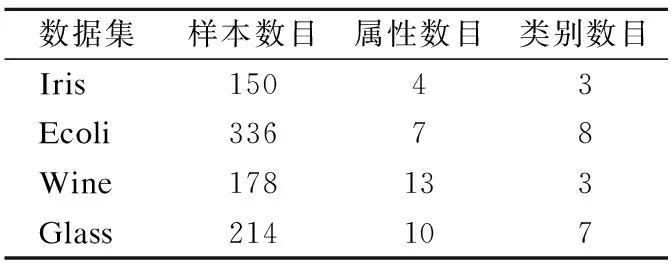
表4 實驗所用數據集Table 4 Datasets used in the experiment

4.3 評價指標

在本實驗中利用聚類精度(Accuracy，ACC)和標準化互信息(Normalized Mutual Information，NMI)來評價聚類性能.

聚類精度：正確分配到聚類的樣本數與所有需要聚類的樣本總數的比值.計算公式如式(16)所示.

(16)

其中，dk表示正確分配給第k個簇的樣本數，N表示所有樣本的數.

標準化互信息：是一種對稱度量，能夠量化兩個集群分布之間共享的統計信息[21].度量公式如式(17)所示：

(17)

其中，R和Q是輸入數據集的兩個分區，分別包括簇I和簇J.P(i)是從數據集中隨機選擇的樣本分配給簇Ri的概率，P(i，j)是樣本同時屬于簇Ri和簇Qi的概率.H(R)是與分區R中的所有概率P(i)(1≤i≤I)相關聯的熵.

實驗結果中準確率數值越大，說明樣本正確分配到對應簇的數量越多，聚類性能越好；標準化互信息數值越大，代表簇之間劃分得越準確，說明算法的聚類效果越好.

4.4 實驗結果

4.4.1 聚類性能對比實驗

將算法FCM、PSOFCM、FAFCM與IFAFCM算法在4個數據集上進行比較.算法參數設置分別為最大迭代次數maxT= 300，模糊指數m值為2，閾值ε為10-5，初始種群數N= 30，最大吸引度β0=1.0，步長因子α= 0.8，冷卻系數δ=0.98，光吸收因子γ= 0.9，粒子加速系數c1=c2=2，r1，r2為分布于[0，1]的隨機數，慣性權重系數Wmax=0.9，Wmin=0.4.將每種算法在各數據集上分別運行10次，求取平均值得到ACC和NMI，對比結果如表5所示.

表5 4種算法評價指標ACC和NMI的結果比較Table 5 Comparison of the results of evaluation indexes ACC and NMI of the four algorithms %

從表5中可以看到，IFAFCM算法在4個數據集上的ACC和NMI兩個指標，均比其他3種算法有明顯提高.其中FCM算法在兩種評價指標中都處于最低.這是由于IFAFCM算法在初始種群分布與搜索能力上都做出了改進，使得在聚類算法中具有較優的聚類中心，提高了聚類性能.其中在Iris數據集中IFAFCM算法在ACC指標上平均提高了2%～4%，在NMI指標上平均提高了6%～10%；在Ecoli數據集中IFAFCM算法在ACC指標上平均提高了4%～10%，在NMI指標上平均提高了5%～8%；在Wine數據集中IFAFCM算法在ACC指標上平均提高了1%～2%，在NMI指標上平均提高了3%～5%；在Glass數據集中IFAFCM算法在ACC指標上平均提高了5%～11%，在NMI指標上平均提高了9%～15%.

4.4.2 抗噪能力

為了進一步體現IFAFCM算法的優越性，設計了抗噪聲對比實驗.在4個原數據集中加入不同比例的噪聲數據，然后分別進行聚類.通過聚類得到的ACC和NMI的數據來反映噪聲數據對各個算法影響程度，實驗結果如圖5和圖6所示.從圖中可以看出IFAFCM算法隨著噪聲比例的增加，ACC和NMI指標在4種算法中均取最大值.可見，IFAFCM算法與其他3種算法相比，具有較好的魯棒性.

圖5 4種對比算法在4個數據集上的聚類精度對比圖Fig.5 Comparison graphs of clustering accuracy of four comparison algorithms on four datasets

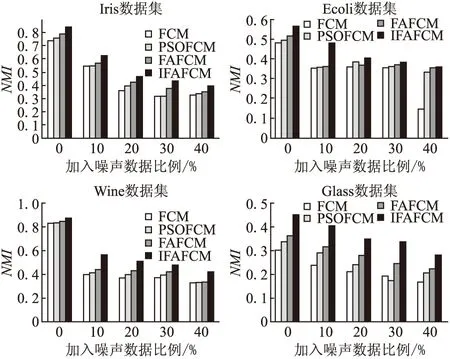
圖6 4種對比算法在4個數據集上的聚類標準化互信息對比圖Fig.6 Comparison graphs of clustering normalized mutual information of four comparison algorithms on four datasets

5 總 結

本文提出了一種改進螢火蟲算法的模糊聚類算法IFAFCM，該算法對傳統FCM初始化敏感、魯棒性差等方面進行了改進，以提高聚類準確率.在該算法中，首先運用Chebyshev混沌映射將螢火蟲種群均勻分布到搜索空間中，生成范圍廣、分布均勻、全局搜索能力強的初始種群；然后將步長因子轉變為動態調整的方式，平衡了探索與開發過程；最后采用高斯擾動對最優個體進行變異，增強了算法跳出局部最優的能力.螢火蟲算法與傳統FCM算法的結合，既提供了良好的全局搜索能力，又保證了良好的局部開發能力.為了評估IFAFCM算法的聚類效果，在4個數據集上與其他3種算法進行了對比實驗，實驗結果表明，IFAFCM算法相較于其他3種算法，在聚類性能、抗噪能力方面均有提高.