一種簡化的基于互相關算法的幀同步處理方法

劉 明

（中國電子科技集團公司第十研究所，四川 成都 610036）

0 引 言

在數字通信中，同步按類型可分為載波同步、碼元同步（位同步）、幀同步以及網同步。其中，幀同步作為一個重要的環節，在數據傳輸過程中起著非常重要的作用[1-3]。對于實時性要求比較高的場合（例如衛星數字通信），幀同步多采用集中插入法將一組特殊碼字序列周期性的插入到每幀數據的最前端，利用這組特殊碼字序列（幀同步碼序列）的有關特性完成幀同步碼檢測。在完成載波同步和位同步的基礎上，從解調器輸出數據中尋找幀同步碼序列的過程被稱為幀同步處理。幀同步處理不僅需要正確標記出每幀數據的起始位置，即完成所謂的幀同步檢測，而且需要根據本地幀同步碼序列的形式解除因鑒相器相位不確定性導致的數據相位模糊。當數字接收機面臨惡劣工作環境時，幀同步處理性能的優劣直接決定后續譯碼的結果。因此，如何正確快速地實現幀同步處理對數字通信至關重要。

當已知幀同步碼序列時，幀同步檢測實際上就是一個碼序列已知而出現時刻未知的檢測問題。針對此類問題，現有實現幀同步檢測的方法有最優似然比檢測、廣義似然比檢測以及相關檢測方法。文獻[4]給出了加性高斯背景下多進制相移鍵控（Mary Phase Shift Keying，MPSK）調制方式下最優似然比檢測形式，并采取一些近似方法簡化最優似然比檢測的形式。文獻[5]在幀同步碼序列已知條件下提出一種修正的基于似然比檢測的幀同步檢測方法，需要根據實際應用環境選擇不同的檢測器形式，以便獲得相對最優的檢測結果。文獻[6]在加性高斯噪聲背景下對比了幀同步最優似然比檢測、廣義似然比檢測以及相關檢測的檢測性能。

與基于似然比類的檢測方法不同，相關檢測方法因形式簡單，在實現幀同步處理方面也獲得廣泛應用[7-9]。幀同步相關檢測算法利用幀同步碼序列的相關特性進行能量累積，當累積后的能量大于某一閾值時，檢測器就認為檢測到了幀同步碼序列。根據參與相關計算的數據類型，相關檢測算法可以分為兩種。一種是以幀同步碼序列自相關為基礎的延遲相關算法，該算法在含有載波偏移時仍具有非常好的檢測特性，但在低信噪比和多經信道下，自相關函數在峰值附近緩慢衰減，不能準確給出幀同步碼序列的起止點。另一種是采用本地幀同步碼序列的互相關算法，該算法對應的相關函數具有尖銳的單峰特性，能準確給出幀同步碼序列的起止點，具備抗噪聲和多徑的能力，但在含有載波偏移時其性能受到限制。針對存在載波偏移的應用場景，文獻[10]提出一種相關窗分隔的相關檢測方法。

不管是哪種相關檢測算法，選取的幀同步碼序列的特性在一定程度會影響到幀同步性能的優劣。一般來講，選取幀同步碼序列應具有明顯的單峰相關特性。常見的可以用來作為幀同步字碼序列有巴克碼、Heuman-Hoffman序列、m序列以及Gold序列。結合這些碼型的特性，國內外學者在這方面做了許多研究工作。文獻[11]通過設計一種具有置換特性的幀同步碼序列，提高傳統幀同步相關檢測方法在頻分復用系統中的性能。文獻[12]選取了巴克碼與優選48比特同步序列的擴展序列作為幀同步碼序列，提出一種極低信噪比下二次相關檢測算法。文獻[13]在m序列的幀同步碼未知條件下，利用m序列的偏三階相關函數的特性實現幀同步碼的識別。這些方法多側重于判斷接收的數據中是否存在幀同步碼序列和幀同步碼序列的確切位置，很少考慮接收數據存在的相位模糊。

在實際衛星數字通信中，幀同步處理不僅完成了幀同步檢測，而且解除了數據中存在的相位模糊，恢復了數據應有的數據形式。目前工程應用中使用的幀同步處理方式有兩種，如圖1（a）、（b）所示。原始的比特流序列依次經過映射、調制、信道傳輸和解調等處理后，最終得到解調器輸出信號I1和Q1。

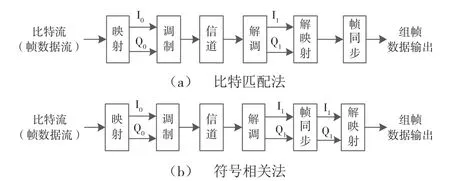
圖1 兩種常見幀同步處理方式

在圖1（a）中，幀同步處理采用比特匹配法檢索幀同步碼字序列，利用解調器輸出數據經解映射后的數據與幀同步字序列的異或結果判斷數據中是否存在幀同步字序列。這種幀同步方法需要遍歷數據中所隱含的相位模糊，幀同步建立時間相對較長。在圖1（b）中，幀同步處理采用本地幀同步碼序列的互相關算法檢索幀同步字序列，利用解調器輸出數據與幀同步字序列經映射后數據的復相關結果，同時完成幀同步檢測和數據相位的解除，幀同步建立時間相對較短。對于較長幀序列的幀同步檢測情形，采用圖1（b）方法對應的幀同步建立時間要明顯少于采用圖1（a）方法對應的幀同步建立時間。

本文采用本地幀同步碼序列的互相關檢測算法，以m序列為幀同步碼序列，依據向量之和的模平方不大于向量模平方之和的結論推導了MPSK調制方式下幀同步相關檢測算法取得最大值的上界，同時給出計算數據相位差的估計算法。鑒于算法工程應用的復雜性，對上述算法進行了簡化。

1 信號模型

在通信系統中，調制器將二進制比特向量b=[b0,b1,…,bm-1]映射到星座圖上的符號，其中m表示與一個符號對應的比特數目。對于MPSK調制方式，其星座圖是由均勻分布在某個圓上的星座點構成，并且這些星座點對應符號的取值都是復值，可以描述為：

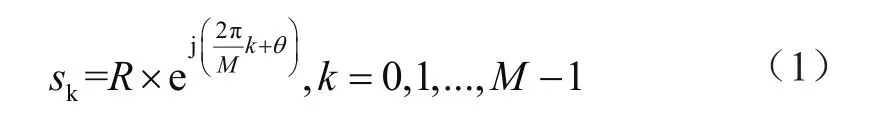
式中，R既表示圓的半徑也表示符號的強度；j表示虛數單位；M表示均勻分布在圓上的星座點數目；θ表示星座點的初始相位。例如在第二代衛星數字電視標準中，正交相移鍵控（Quaternary Phase Shift Keying，QPSK）和8移相鍵控（8 Phase Shift Keying，8PSK）星座圖分別對應式（1）在M=4且初始相位為π/4與M=8且初始相位為0的情形。

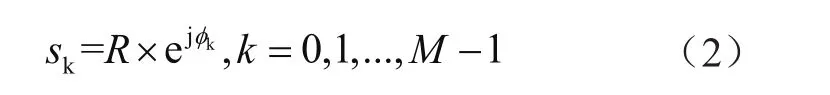
經過調制、信道傳輸、成型濾波、采樣和量化等處理過程，最終得到解調器的輸入信號。假設載波信號和定時信息完全可以正確恢復，那么解調器輸出的最終信號形式為：

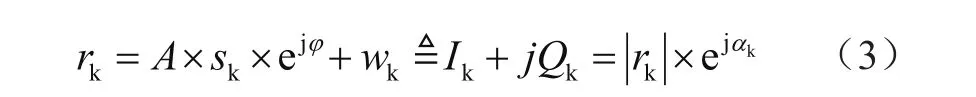
式中，A表示信道增益；φ表示因解調時鑒相器不確定性導致的相位差；wk表示均值為0、方差為σ2的復白高斯分布隨機變量；|·|表示取模運算；αk表示相位。

2 m序列定義及產生

m序列是最長線性反饋移位寄存器的簡稱，它是由帶線性反饋移位寄存器產生的周期最長的序列。圖2為n級線性反饋移位寄存器網絡的原理圖。

圖2 線性反饋移位寄存器原理

假設當前移位寄存器的狀態為An-1An-2…A1A0，經過一次移位后，移位器左端得到新的輸入An。由圖中連接關系可知：

式中，mod2表示模2運算；ci表示反饋線的連接狀態（ci=1表示參與反饋，ci=0表示不參與反饋）。將n個系數組成的向量c=[c0,c1,…,cn-1]稱為線性反饋移位寄存器的特征多項式，當特征多項式為既約多項式時，此時的線性反饋移位寄存器末端的輸出即為m序列。

除此之外，m序列具有較好的均衡性和自相關特性。在m序列的一個周期中，“1”的個數比“0”的個數多一個。自相關函數具有顯著的單峰特性，在0偏移時取得最大值1，其余各點取值為其周期的倒數的相反數。

3 互相關檢測方法

互相關檢測算法通過計算本地幀同步碼序列映射信號和解調器輸出信號的互相關函數，由互相關函數的極值和取得極值時的兩組信號的相位差分別確定幀同步碼字的確切位置和發送數據與接收數據之間存在的相位差。根據相位差調整解調器輸出信號的相位，從而在實現幀同步碼序列檢測的同時解除數據中的相位模糊。

假設完整的一幀數據映射后是由N個符號構成，其中前L個符號與幀同步碼序列相對應（這里假設幀同步序列位于每幀數據的起始位置），剩余的N-L個符號與傳輸的數據相對應。此外，假定傳輸數據對應的這些符號均勻分布在星座圖上。定義集合{s0,s1,…,sL-1}表示本地幀同步碼碼序列經MPSK調制方式星座映射后的復信號序列、集合{r0,r1,…,rN-1,}表示解調器接收端收到任意一組長度為N的復信號序列，那么互相關檢測算法可以表示為：

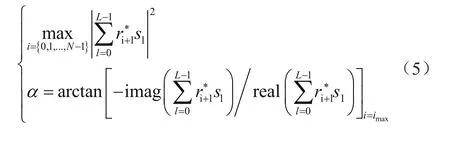
4 實驗結果與性能分析

為了驗證簡化后相關檢測方法和相位估計方法的有效性，采用仿真的方法對比了簡化前后兩種方法的性能。理論上，對于低階MPSK調制方式，簡化前后統計量具有相同的形式，故這里以文獻[14]中定義的8PSK調制方式為例進行實驗。實驗中用到參數設置如下：幀同步字序列經映射后的復信號長度分別設置為L=16、32、48、64，數據對應的符號長度為4 096，相關檢測門限設置為L點功率之和的1/2，每種參數設置條件下發送數據幀數目為500 000個。

首先分析了不同條件下簡化前后兩種相關檢測算法的漏檢概率和虛警概率。作為幀同步性能的重要指標，經常會使用漏檢概率和虛警概率分析其性能。其中，漏檢概率是指判決器遺漏接收序列中真實幀同步字序列的概率，虛警概率是指判決器錯誤地將數據序列誤認為幀同步字序列的概率。兩種相關檢測的漏檢概率如圖3所示。

相同符號長度條件下，兩種相關檢測器僅存在細微的差異。符號長度越長，漏檢概率越低。當符號長度大于32時，漏檢概率幾乎都小于0.01。當此時的幀同步處理引入狀態機保護機制時，漏檢概率會急劇減小。例如，當設置幀同步保護幀數為3幀時，真實的漏檢概率將是圖3中曲線取值的3次方，這對幀同步平均建立時間的影響是極小的。

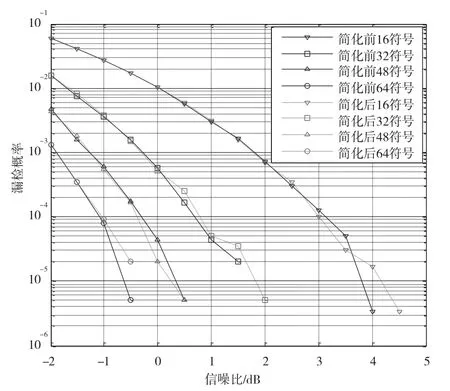
圖3 不同長度符號對應的漏檢概率曲線

兩種相關檢測的虛警概率或假同步概率統計如表1所示。

由表1可知，當采用16個符號進行相關檢測時，兩種相關檢測器的虛警概率都偏高。當選取的符號長度較短時，數據中出現了與同步字符號的相似的符號概率會增大，從而導致過多的虛警概率。圖4給出信噪比為6時使用16個符號作相關檢測時統計量（灰色曲線）過門限情形，其中黑線表示使用的門限值。

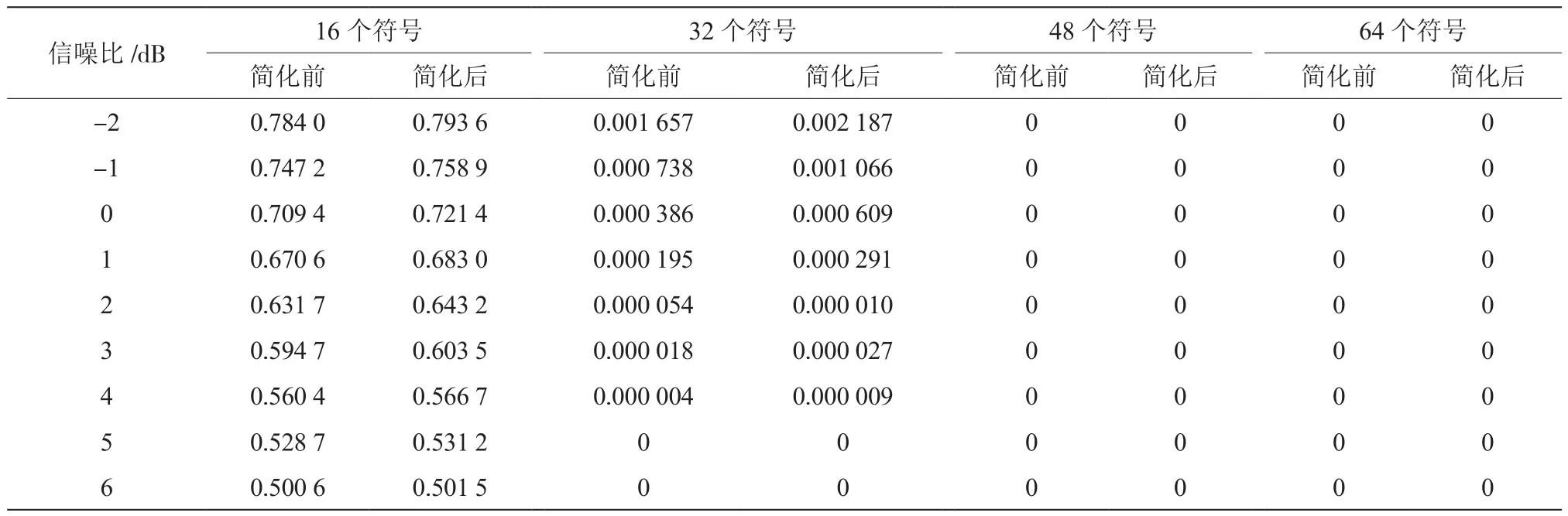
表1 兩種相關檢測器對應的假同步概率(×10-4)

從圖4可知，除了幀同步字所在位置出現過門限的峰值外，其余位置也出現了過門限的峰值，正是由于這些峰值的存在，導致此時檢測器虛警概率偏大。對于這些虛警點，由式（5）或式（11）計算所得的相位差多數將遠遠偏離實際的相位差，最終導致解映射后數據的比特誤碼率（Bit Error Ratio，BER）曲線惡化。當采用32、48和64個符號作相關檢測時，在信噪比靠近0 dB附近，虛警概率基本在10-4水平及以下。此時，若幀同步處理引入狀態機保護機制，虛警概率會急劇減小。

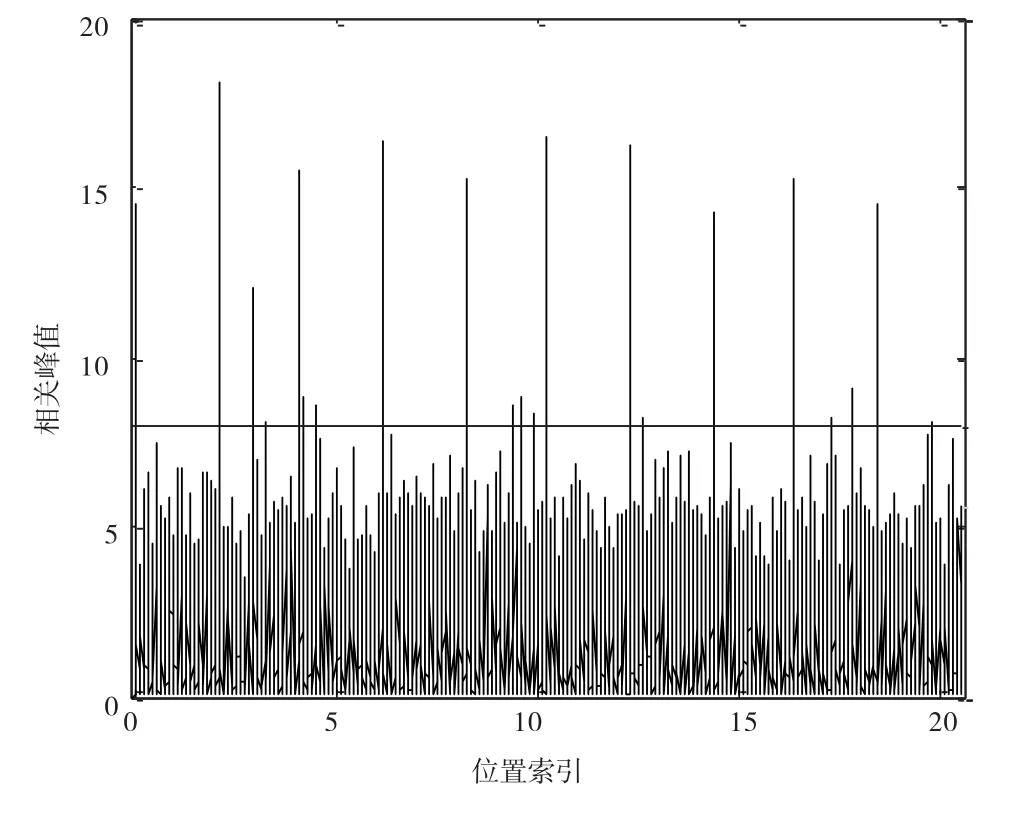
圖4 采用16個符號時檢測統計量分布情形

為了衡量兩種相關檢測算法估計相位差的精準程度，定義歸一化絕對相位差為兩種估計方法所得相位差之差的絕對值與2π的比值。不同長度符號對應的歸一化絕對相位差如圖5所示。

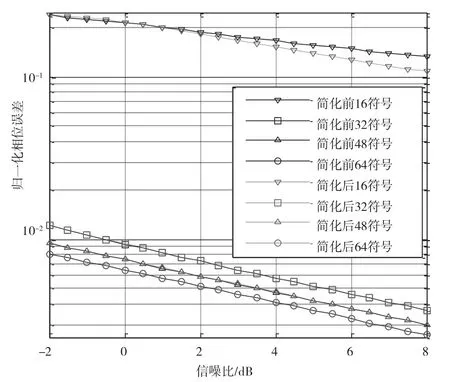
圖5 不同長度符號對應的歸一化絕對相位差

由圖5可知，隨著信噪比的增大，歸一化絕對相位差逐漸減小。隨著相關檢測使用符號數目的增多，歸一化絕對相位差依次遞減。當選取幀同步序列稍微長（符號長度大于等于32時），即使在噪聲嚴重干擾下，兩種估計相位差的方法均能有效的工作。

為了充分說明簡化前后算法的近似程度，采用BER曲線進行對比，結果如圖6所示。

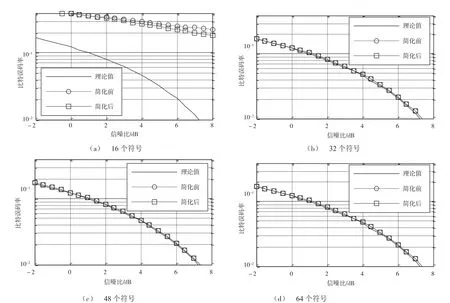
圖6 不同長度符號對應的兩種檢測器的BER曲線

當選取的幀同步序列較短（如選16個符號）作相關檢測時，兩種相關檢測器相比理論曲線有較大的性能差異，這是由于傳輸數據中出現類似幀同步序列的內容，導致檢測過程中出現過多的虛警；當選取的幀同步序列稍微長一些（例如32、48和64個符號）作相關檢測時，兩種相關檢測器相比理論曲線有較細微的性能差異，并且兩種相關檢測器的性能幾乎是相同的。表2給出了兩種檢測器在不同信噪比條件下與理論曲線之間的差值。

從表2中可以看出：一方面，隨著信噪比的增大，兩者與理論曲線之間的差值逐漸減小；另一方面，隨著參與相關檢測符號數目的增多，兩者與理論曲線之間的差值也逐漸減小。

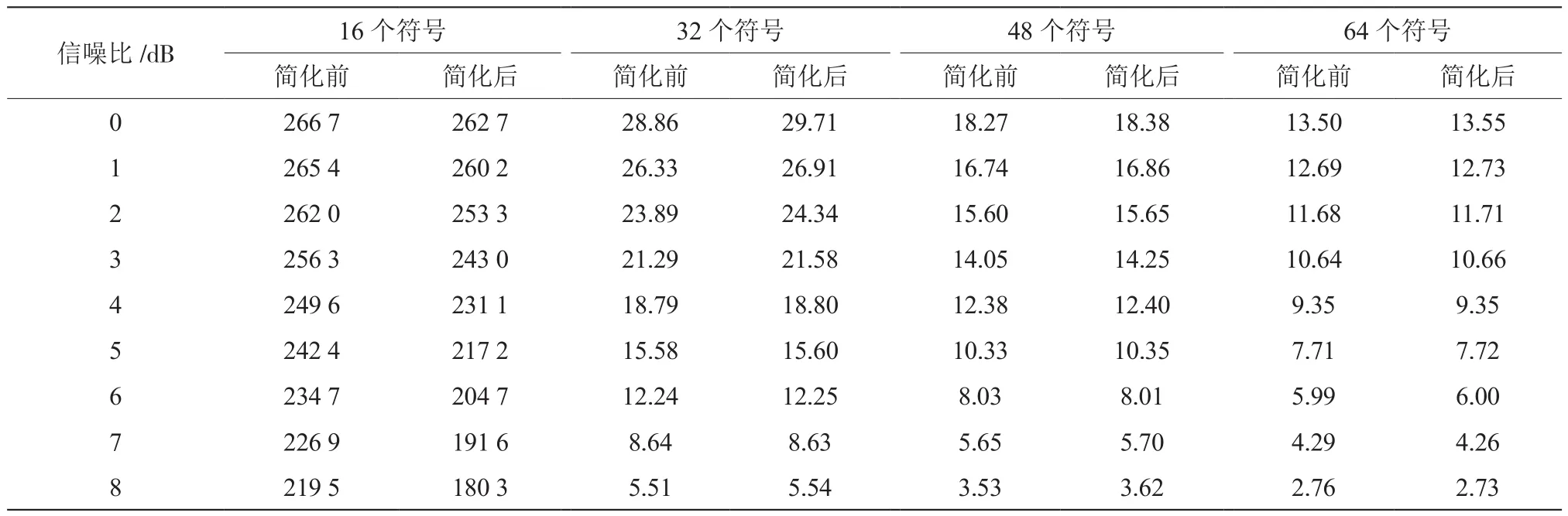
表2 兩種相關檢測器BER曲線與理論BER曲線的差值(×10-4)

5 結 論

根據向量之和的模平方小于等于向量的模平方之和的推論，分析了MPSK調制模式下幀同步檢測問題的相關檢測算法和相位估計算法。基于相位估計算法的復雜性，提出一種簡化的相位估計算法，簡化前后的相關檢測算法具有相同形式。在仿真條件下，以8PSK為例對比兩種相關檢測算法和兩種相位估計算法的性能。實驗結果表明，當選取合適長度的具有單峰特性的m序列作為的幀同步字序列時，簡化前后的兩種算法具有幾乎同等的性能。當引入幀同步狀態機保護機制時，兩種方法具有極低的漏檢概率和虛警概率，幾乎不影響幀同步建立時間。相比簡化前的算法，簡化后的算法因具有更少的運算量更容易在工程應用實現。