插入式封隔器注水管柱力學及蠕動規律研究

季公明，郭宏峰，杜曉霞，李 翔，趙廣淵，楊樹坤，李嘯峰

(中海油田服務股份有限公司 天津分公司，天津 300459)

分層注水是解決層間矛盾、調整吸水剖面，提高油田開采效率及實現油田資源穩定高效開采的重要措施。在分層注水施工和實際生產過程中，海上多層段分層注水管柱在井下承受拉、壓、彎、扭、流體壓力等多種載荷，并受到活塞效應、鼓脹效應、彎曲效應、溫度效應(以下簡稱4種效應)的影響；海上注水井分注層段多且單層注入排量大，使得管柱受力及管柱蠕動狀況更加復雜，井下溫度變化以及井況參數等因素易造成注水管柱變形嚴重，甚至可能造成管柱斷脫、管柱永久性螺旋彎曲、封隔器中心管斷裂、封隔器密封損壞等，從而導致注水管柱失效，產生巨大的經濟損失[1-6]。

為了研究實際作業過程中注水管柱的受力狀況、溫度變化規律、管柱變形規律和封隔器蠕動規律，本文在諸多學者研究的基礎上，針對插入式封隔器注水管柱的力學及蠕動規律進行研究，從而設計更安全的管柱結構，并提供分析數據，指導分層注水參數的合理選擇，避免發生管柱失效事故，延長注水管柱的工作壽命[7-15]。

1 插入式封隔器管柱結構特點

插入式封隔器通過密封模塊與密封筒內壁之間的過盈配合來實現密封。圖1為插入式封隔器的結構示意圖。

a 密封接觸面示意

b 插入密封與密封筒配合結構示意

由于插入式封隔器是過盈配合，對密封筒內孔的表面質量提出了更高的要求，必須達到一定的粗糙，并且不能有損傷或者腐蝕。密封模塊的過盈也要控制在一定范圍內，如果太大，在插入密封時會出現劃傷，太小則無法保證密封。

插入密封的特點是結構簡單，便于操作，因此在海上油田被廣泛使用。

2 注水管柱力學分析模型

注水管柱在井筒中的受力情況非常復雜，為真實反映管柱在井筒中的實際受力狀態，充分考慮摩擦、內外壓、粘滯摩阻、井斜角、井眼彎曲等各種因素的綜合影響，結合管柱的4種效應，建立管柱的三維力學分析模型[16-20]。如圖2所示。

圖2 分層注水管柱的三維力學分析模型

注水管柱在其工作工況中處于平衡狀態，其力學平衡方程為

(3)

3 注水管柱蠕動分析

3.1 蠕動機理研究

圖3 封隔器受力模型

該處的力學平衡方程為：

整理得：

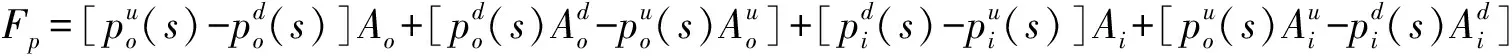
FΔτ+Fp=f

(7)

式中：封隔器位置上、下節點間真實軸向力的差值用FΔτ來表示；力的作用點在封隔器處的壓力引起的力用Fp來表示；軸差力通過FΔτ和Fp這2個力的和來計算；密封筒對膠筒所產生的摩擦力用f來表示。

若膠筒最大靜摩擦力為fmax，當FΔτ+Fp>fmax，軸差力大于保持平衡的上界，也就是大于膠筒的最大靜摩擦力fmax，膠筒此時會處于受力不平衡狀態，產生軸向運動，稱之為管柱蠕動現象。

3.2 管柱蠕動分析流程

軸差力可通過如下方式進行計算：假設管柱處于受力平衡狀態，不產生管道蠕動現象。則膠筒軸向位移為零，即邊界條件為Δujt=0，結合管柱力學效應，FS的值通過循環反饋的流程便可以計算出來。計算流程如圖4所示。

圖4 等效軸差力的計算流程

當膠筒由于受力不平衡產生軸向運動后，會在新的位置再次保持平衡狀態，由原位置到新的平衡位置的軸向距離的插值就是需要求解的蠕動量。原位置已知，膠筒的新平衡位置可以由4種效應理論計算得出。需要先確定管柱各個節點上的等效軸力。等效軸力可以由圖4的計算流程得出。

以封隔器數目為n，配水器數目也為n的n級n段注水管柱為例。將封隔器下入定為起始狀態。在第n級封隔器不出現蠕動的條件下，分析第n-1級的受力情況，并判斷是否發生蠕動。如果n-1級封隔器出現蠕動，則對其蠕動量和自由移動變形進行計算。如果未出現蠕動，計算該級管柱受力的變化后，計算n-2級封隔器的受力。按照此方法類推到封隔器的第1級。在n級n段注水管柱中，具體的蠕動計算流程如圖5[21]。

圖5 n級n段管柱蠕動分析流程

4 插入式封隔器摩擦力分析

有限元模擬法是獲取膠筒與密封筒間的最大靜摩擦力的有效方法之一。通過分析膠筒有限元模型上的接觸應力后，在膠筒與密封筒的接觸節點處獲取其接觸應力和位移。存在于密封筒和膠筒之間的總接觸應力可以通過積分的方法獲得，即，在接觸面上對接觸應力作積分運算，從而獲得最大靜摩擦力。

1)選取單元類型。

封隔器中心管、密封筒、膠筒等部件采用plane182單元。根據膠筒與中心管、密封筒的接觸特點選擇剛性-柔性接觸。目標單元為其它件與膠筒的接觸面，單元類型為target169;接觸單元選擇膠筒接觸面，單元類型為contal172。

2)設置材料特性。

阿氟拉作為一種超彈性材料，是插入式封隔器膠筒常用材料之一。本文采用超彈性材料模型Mooney Rivlin來計算。根據試驗數據，模型參數設置為：C10=3.056，C01=0.764；泊松比為0.49，彈性模量為22.92 MPa。密封筒彈性模量為209 GPa，泊松比為0.269。中心管材料為9Cr1Mo，彈性模量為236 MPa，泊松比為0.3。

模擬插入坐封的過程，邊界調節設置為：密封筒、中心管在y方向約束，密封筒向左移動1 mm位移，表示插入擠壓膠筒過程。其接觸應力計算結果如圖6所示。

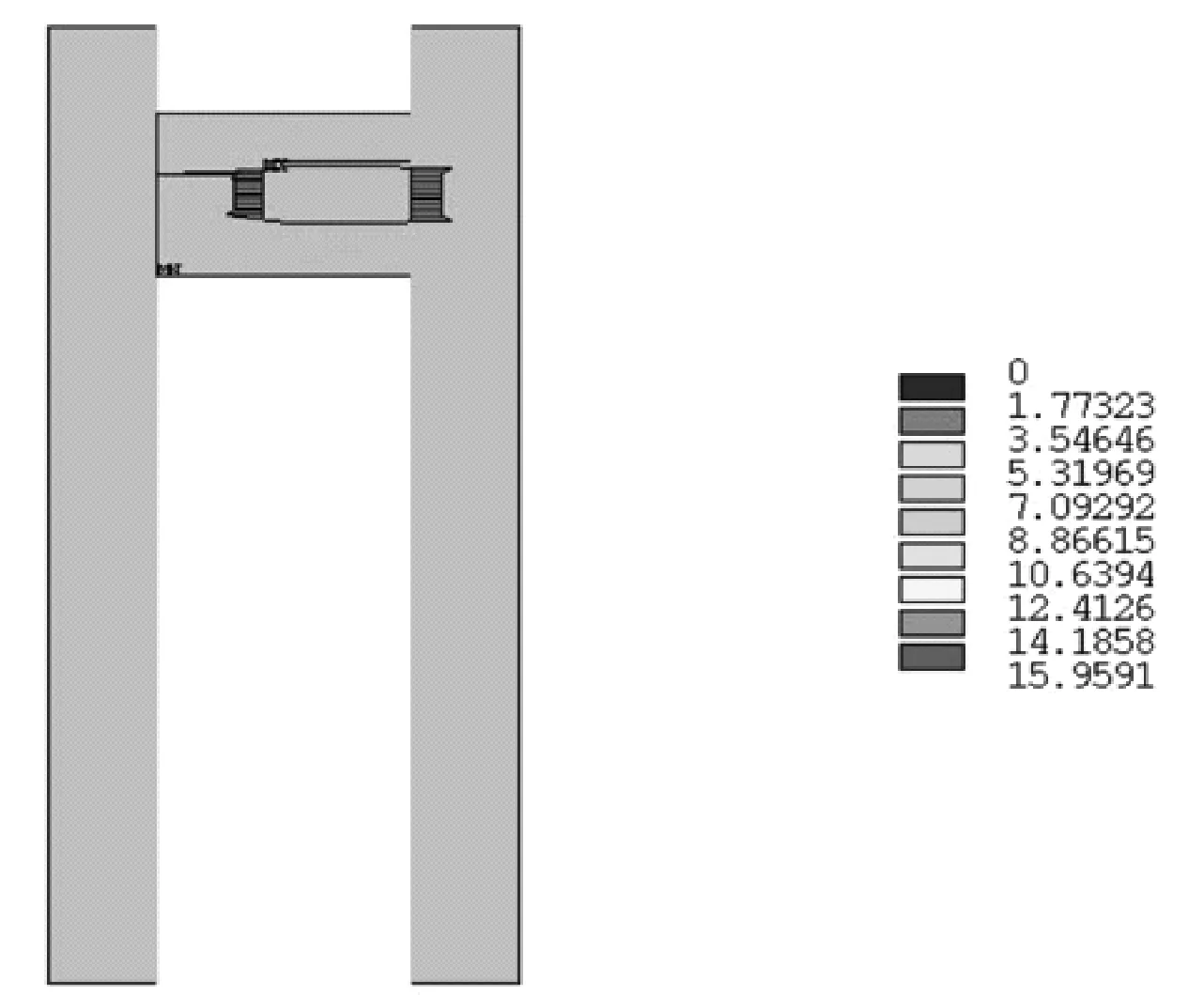
圖6 插入式封隔器接觸應力云圖

在得到膠筒與密封筒間的徑向接觸應力之后，運用數值積分的方法，可以得到在膠筒與密封筒之間的總接觸力為52.41 kN，膠筒與密封筒之間的最大靜摩擦力為15.72 kN。

5 實例計算

實例井的井深為2 660 m，最大井斜角為71.3°。對無錨定插入式封隔器注水管柱進行軸力及蠕動量計算，得到其管柱下入及起出受力情況。如表1所示。

表1 各工況下分注管柱力學分析結果

在注水作業過程中，井口壓力12 MPa，套壓0 MPa，注水量525 m3/d，注水溫度20℃。工況變化為：注水60 h，停住12 h，增產措施4 h，注水24 h。管柱的蠕動量如圖7所示。

圖7 不錨定管柱全工況作業的管柱蠕動規律

在注入和增產措施工況下，由于排量、注水溫度、井口壓力等因素變化，導致插入式封隔器膠筒所提供的摩擦力不足以阻止軸差力引起管柱收縮，從而帶動插入式封隔器向上蠕動；在停注工況，注水井井筒回溫，管柱長度隨之一起恢復，從而帶動插入式封隔器向下蠕動。

該管柱各工況下的蠕動量在-0.8～1.0 m。由于軸向力會在各級封隔器間傳遞，因此各級封隔器發生的蠕動變化幾乎一致，即，蠕動量幾乎相等；在工況轉換過程中，全管柱最大蠕動量為1.8 m，未超出安全長度，且實例井封隔器正常工作，沒有出現密封失效的竄層現象。

此外，對多口實例井開展蠕動量計算，均與現場實際井況較符合，從而反映出該蠕動算法的可靠性。

6 蠕動規律研究

注水壓力12 MPa，注入排量525 m3/d，注入液溫度20 ℃，分注管柱為4級4段。在該注水管柱第1級封隔器上端和第4級封隔器下端安裝水力錨，對某井注水管柱進行蠕動量計算，分析出其蠕動規律，如圖8所示。

a 第1級封隔器上方錨定

b 第4級封隔器下方錨定

頂部施加錨定后，第4級封隔器向上收縮0.33 m，與頂部未錨定管柱相比，第4級封隔器處蠕動小了0.35。底部施加錨定后，第4級封隔器向上收縮0.28 m，與底部未錨定管柱相比，第4級封隔器處蠕動小了0.41 m。無論頂部和底部施加錨定，都可以減緩管柱的蠕動量，而且在最下方錨定的效果要優于上方錨定。

現場應用井，注水壓力層間壓差為1～7 MPa。將第1～4配水層段節流壓差均設置為1 、3、5、7 MPa，其他層段節流壓差均設置為1 MPa，分析最高節流壓力在不同層段下錨定與不錨定的管柱蠕動量變化規律。

1)大節流壓差不錨定管柱蠕動量變化規律。

如圖9所示。注水管柱的蠕動量對最下層壓差變化較為敏感；在其它層段壓差變化時，管柱的蠕動量變化較小；當節流壓差達到一定值時管柱自身也能起到錨定作用，但封隔器長期需要承受大壓差，對膠筒傷害較大。

a 第1層大節流壓差

b 第2層大節流壓差

c 第3層大節流壓差

d 第4層大節流壓差

2)大節流壓差錨定管柱蠕動量變化規律。

如圖10所示。在錨定狀態下，管柱蠕動比不錨定狀態下要小。因此，應根據油藏細分層注水開發需求，加入錨定結構確保插入式封隔器蠕動量在安全范圍內。在管柱錨定情況下，恰當的大節流壓差能夠減小管柱的蠕動，延長管柱作業壽命。

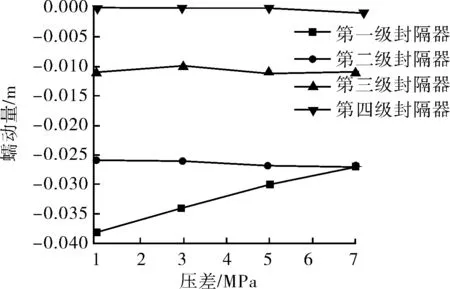
a 第1層大節流壓差

b 第2層大節流壓差

c 第3層大節流壓差

d 第4層大節流壓差

7 結論

1)建立多層段分層注水管柱力學模型，分析管柱蠕動機理。考慮插入式封隔器位置錨定力、摩擦力及4種效應的綜合影響，提出了多級多段注水管柱蠕動量分析流程。

2)以某井為例，在下入、注水、停注、增產措施、起出等不同工況下，進行注水管柱受力分析及蠕動量計算。通過與實際對比，證實本文所提出的蠕動分析模型的可靠性，并提出防蠕動措施。