撫育采伐強度對天然落葉松林林分結構和蓄積的影響1)

李存慶 董靈波 劉兆剛

(森林生態系統可持續經營教育部重點實驗室(東北林業大學)，哈爾濱，150040)

林分結構是森林經營和分析中的一個重要因子，是對林分發展過程，如更新方式、競爭、自稀疏和經歷的干擾活動的綜合反映[1]，林分結構的合理與否對林分蓄積的影響是至關重要的。根據是否與距離有關，林分結構分為非空間結構和空間結構，非空間結構包括林分物種多樣性、冠層結構、樹種組成、林木徑級結構以及更新特征等[2-6]，空間結構包括樹種隔離程度、林木競爭、林木分布格局等[7-9]。撫育采伐作為森林可持續經營的一項重要措施，會對森林的林分結構產生重要影響，科學合理的撫育采伐有助于改善林分結構，促進森林可持續經營。近些年，針對撫育采伐對林分結構和蓄積的研究很多[3，10-11]。這些研究主要通過方差分析、回歸分析等方法進行分析，但都無法描述影響因素對評價指標的直接影響、間接影響和總影響以及多個影響因素與評價指標之間的交互作用。結構方程模型(SEM)整合了路徑分析、多元回歸和因子分析，可同時分析多個因果關系，這是傳統方法所不具備的[12]。結構方程模型目前已被廣泛應用到心理學、醫學、經濟學、衛生統計等方面[13-16]，但在林業領域應用很少[17-18]，有廣泛的應用前景。

本研究以大興安嶺天然落葉松林為研究對象，在已有研究成果基礎上選取林分結構指標，以林分結構(ξ1)為評價指標及分別以林分非空間結構(ξ2)和林分空間結構(ξ3)為評價指標，并加入撫育強度(T)、林分單位蓄積(V)構建結構方程模型，分析撫育采伐與林分結構、林分蓄積之間的因果關系，以期為該地區森林的可持續經營提供參考。

1 研究區概況

研究區域位于大興安嶺地區新林林業局(123°41′～125°25′E，51°20′～52°10′N)，林分類型為天然落葉松林。該地區地勢較為平緩，為寒冷濕潤氣候區，氣溫年較差和日較差都很大，年平均積溫不足1 600 ℃，屬于寒溫帶大陸性氣候。該地區最高氣溫可達到37.9 ℃，最低氣溫達到-50.1 ℃，年降水量為513.9 mm，且分布不均，主要降水多集中在7—8月份。主要喬木樹種為興安落葉松(Larixgmelinii)，還有白樺(Betulaplatyphylla)、山楊(Populusdavidiana)、樟子松(Pinussylvestrisvar.monggolica)等；下層植被主要為杜香(LedumpalustreL.)、越橘(Vacciniumvitis-idaeaLinn.)等[19]。

2 研究方法

2.1 樣地調查

在全面踏查的基礎上，2018年7—9月份在大興安嶺新林及翠崗林場對2012年進行撫育的天然落葉松林共計83塊樣地進行調查。樣地撫育方式為下層撫育，樣地大小為20 m×30 m，測量并記錄樣地的樣地號、大小、海拔、樹種、胸徑(D≥5 cm)、樹高、相對坐標位置、撫育強度以及林下更新數量等。樣地基本信息見表1。

表1 撫育樣地基本信息

2.2 指標選取

本文依據已有研究，篩選能夠更好地評價林分結構的指標，分別為平均胸徑(D)、樹種組成指數(Z)、更新豐富度(R)、Simpson指數(S)、全混交度(MCi)、角尺度(W)等。

平均胸徑D=(∑di)/N，i=1、2、…、N。式中：N為林木株數；di為第i樹種胸徑。

樹種組成指數(Z)是反映林分樹種多樣性的定量指標，計算公式[20]為Z=-∑(pilogpi)，i=1、2、…、n。式中：n為樹種個數；pi為第i樹種蓄積比例；log為以10為底的對數。

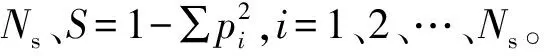
全混交度(MCi)不僅考慮了空間結構單元中鄰近木之間的隔離程度，還考慮了林分空間結構單元的物種多樣性Simpson指數，計算公式[21]為MCi=(1/2)(Di+Ci/ni)Mi。式中：MCi為中心木i的全混交度；Di為中心木i所在空間結構單元的Simpson指數；Mi為簡單混交度；Ci為對象木的最近鄰木中成對相鄰木非同種的個數；ni為最近相鄰木株數。

角尺度(W)作為一個測度林木空間分布格局的林分結構參數，對林木分布具有良好的判別能力，計算公式[22]為Wi=(1/4)∑Zij，j=1、2、3、4。式中：Zij定義為一個離散變量，當中心木比第j株相鄰木小時Zij=1，反之，Zij=0。

對林分指標及林分單位蓄積(V)進行計算，需要說明的是，林分角尺度的取值范圍為Wi∈(0,1]，它的最優值為接近0.5的隨機分布，為了更好地進行數據分析，將角尺度值同時減去0.5并取絕對值，使其范圍變為Wi∈(0,0.5]，最優值為接近0的數值[23]。

2.3 模型構建及數據處理

與傳統的多元回歸、方差分析、路徑分析等不同，結構方程模型并不局限于觀察變量因果關系的分析，結構方程模型是在路徑分析模型的基礎上發展起來的通過對變量協方差進行關系建模的多元統計方法[24]。結構方程模型可分解為兩部分：測量模型和結構模型，模型構建及分析步驟可分為三步[25]：①理論分析及模型設定——模型構建須在已有的研究結果或理論基礎上提出理論模型，包括指標的選取、變量之間關系的假設等。②模型識別及指標篩選——一般模型分析所用的樣本數量為指標數量的10倍以上，即認為模型可識別，然后在模型識別的基礎上進行指標篩選。③模型分析及評價——數據建模時，一般采用極大似然估計(ML)，有研究指出，數據的偏態及峰態(絕對值)分別小于2和7時(中度非正態)，采用極大似然估計是可以接受的[26]。模型構建完成后需進行模型評價，評價指標有比較擬合指數(ICF)、卡方自由度比(χ2/df)、標準化殘差均方根(RSRM)等。

本研究選取平均胸徑(D)、樹種組成指數(Z)、更新豐富度(R)、Simpson指數(S)、全混交度(MCi)、角尺度(W)等6個指標，樣本數量為83個，滿足10倍以上樣本量的要求，且數據偏態及峰態絕對值均分別小于2和7，因此采用極大似然估計對模型進行估計具有可靠性，建模前已對數據進行標準化處理。數據處理及模型構建通過軟件R3.4.3、MPLUS7.4完成。

3 結果與分析

3.1 林分空間指標

由表2可見，輕、中、重度采伐林分與對照組(CK)林分相比，林分平均胸徑(D)均有所增加，其中重度采伐林分的林分平均胸徑最高(12.64 cm)；輕、中、重度采伐林分的樹種組成指數(Z)、更新豐富度(R)、Simpson指數(S)等指標與對照組林分相比并無明顯變化，其中中度采伐林分的樹種組成指數(0.251 0)略高于其它組；輕、中、重度采伐林分與對照組林分相比，全混交度(MCi)均有所增加，其中中度采伐林分的全混交度(0.231 9)略高于其它組；輕、中、重度采伐林分的角尺度(W)指標均高于對照組，但輕、中、重度3組采伐林分的角尺度隨著撫育強度增加而降低。以上結果均依據指標均值進行分析，且結果不具同質性，不能很好地描述撫育強度對林分結構和蓄積的影響，因此本研究構建結構方程模型。數據的偏度和峰度絕對值分別小于2和7(見表3)，表明數據處于中度非正態，可用于數據建模。

表2 撫育樣地林分結構指標信息

表3 林分結構參數指標統計量

3.2 評價指標為林分結構的結構方程模型

撫育采伐對林分結構和林分蓄積均有一定的影響，林分結構同樣也會對林分蓄積產生影響。在此基礎上，本研究用平均胸徑(D)、樹種組成指數(Z)、更新豐富度(R)、Simpson指數(S)、全混交度(MCi)、角尺度(W)等林分結構指標評價林分結構(ξ1)，加入撫育強度(T)及林分單位蓄積(V)構建結構方程模型(模型1)，模型評價指標的比較擬合指數(ICF)為0.865，大于可接受值0.7；標準化殘差均方根(RSRM)為0.078，小于臨界值0.08；卡方自由度比值為1.95，其值小于5；因此模型擬合較好[17]，模型擬合結果見圖1及表4(模型運行前數據已進行標準化)。

由圖1、表4可見：平均胸徑(D)、樹種組成指數(Z)、更新豐富度(R)、Simpson指數(S)、全混交度(MCi)、角尺度(W)等指標，可以很好地評價林分結構(ξ1)；參數估計顯著性，基本達到顯著水平。

模型1中，撫育強度(T)與林分結構(ξ1)的相關系數為0.108，表明撫育強度與林分結構呈正相關，即隨著撫育強度的提高，林分結構趨于優化；撫育強度(T)與林分單位蓄積(V)的相關系數為-0.221，表明撫育強度與林分單位蓄積呈負相關；林分結構(ξ1)與林分單位蓄積(V)的相關系數為0.285，表明林分結構與林分單位蓄積呈正相關，即隨著林分結構的優化，林分單位蓄積是增加的。

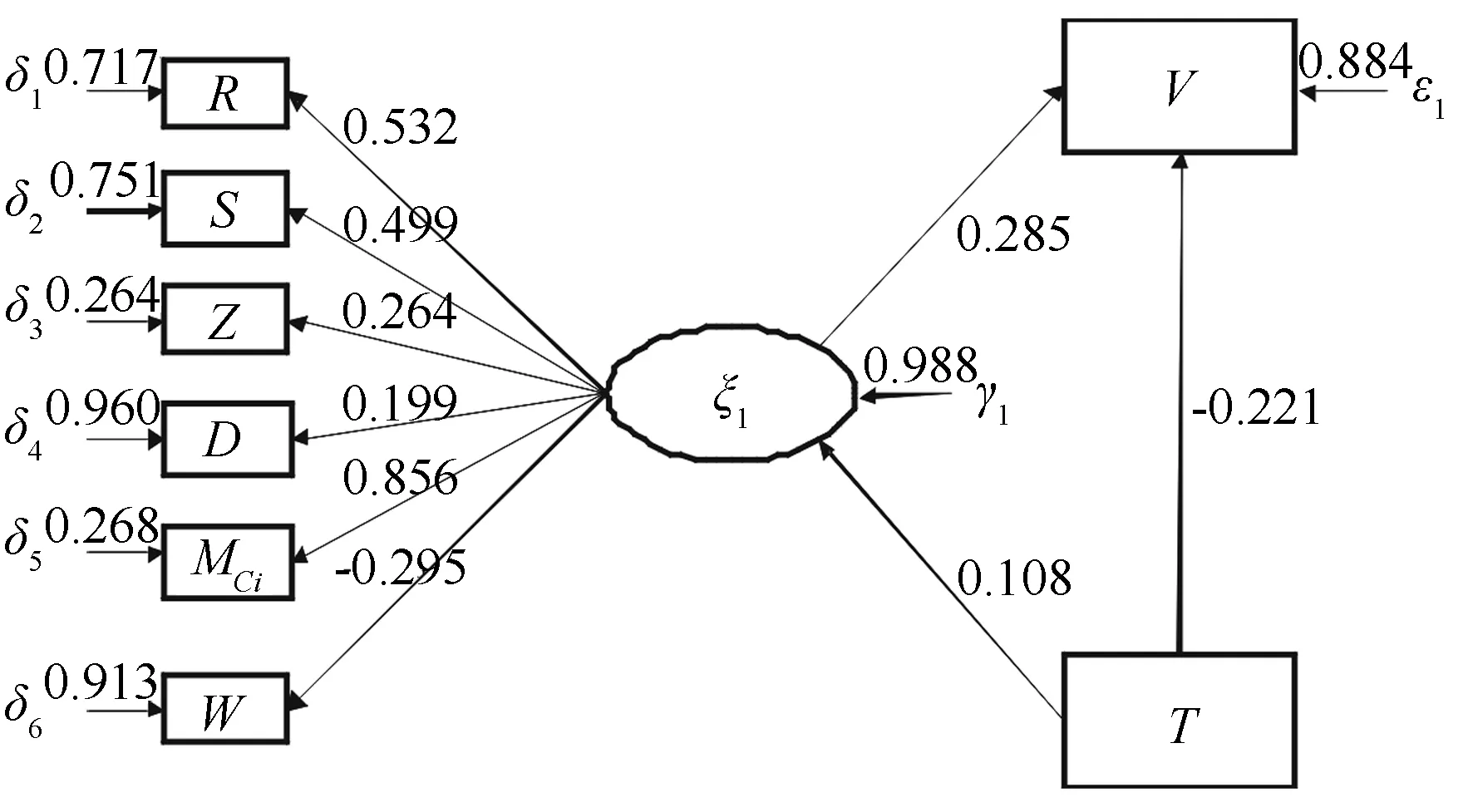
D為平均胸徑，Z為樹種組成指數，R為更新豐富度，S為Simpson指數，MCi為全混交度，W為角尺度，V為林分單位蓄積，δ、ε為測量誤差，γ為殘差值。

表4 模型1參數顯著性估計

3.3 評價指標為林分非空間結構、空間結構的結構方程模型

林分結構可分為林分非空間結構、林分空間結構，為了更好地分析撫育采伐與林分結構、林分蓄積之間的關系，本研究用平均胸徑(D)、樹種組成指數(Z)、更新豐富度(R)、Simpson指數(S)等指標評價林分非空間結構(ξ2)，用全混交度(MCi)、角尺度(W)等指標評價林分空間結構(ξ3)，加入撫育強度(T)及林分單位蓄積(V)構建結構方程模型(模型2)，模型評價指標的比較擬合指數(ICF)為0.844，大于可接受值0.7；標準化殘差均方根(RSRM)為0.079，小于臨界值0.08；卡方自由度比值為2.23，其值小于5；因此模型擬合較好，模型擬合結果見圖2、表5(模型運行前數據已進行標準化)。

由圖2、表5可見：平均胸徑(D)、樹種組成指數(Z)、更新豐富度(R)、Simpson指數(S)等指標，可以良好地評價林分非空間結構(ξ2)；全混交度(MCi)、角尺度(W)等指標，也可以很好地評價林分空間結構(ξ3)；參數估計顯著性，基本達到顯著水平。

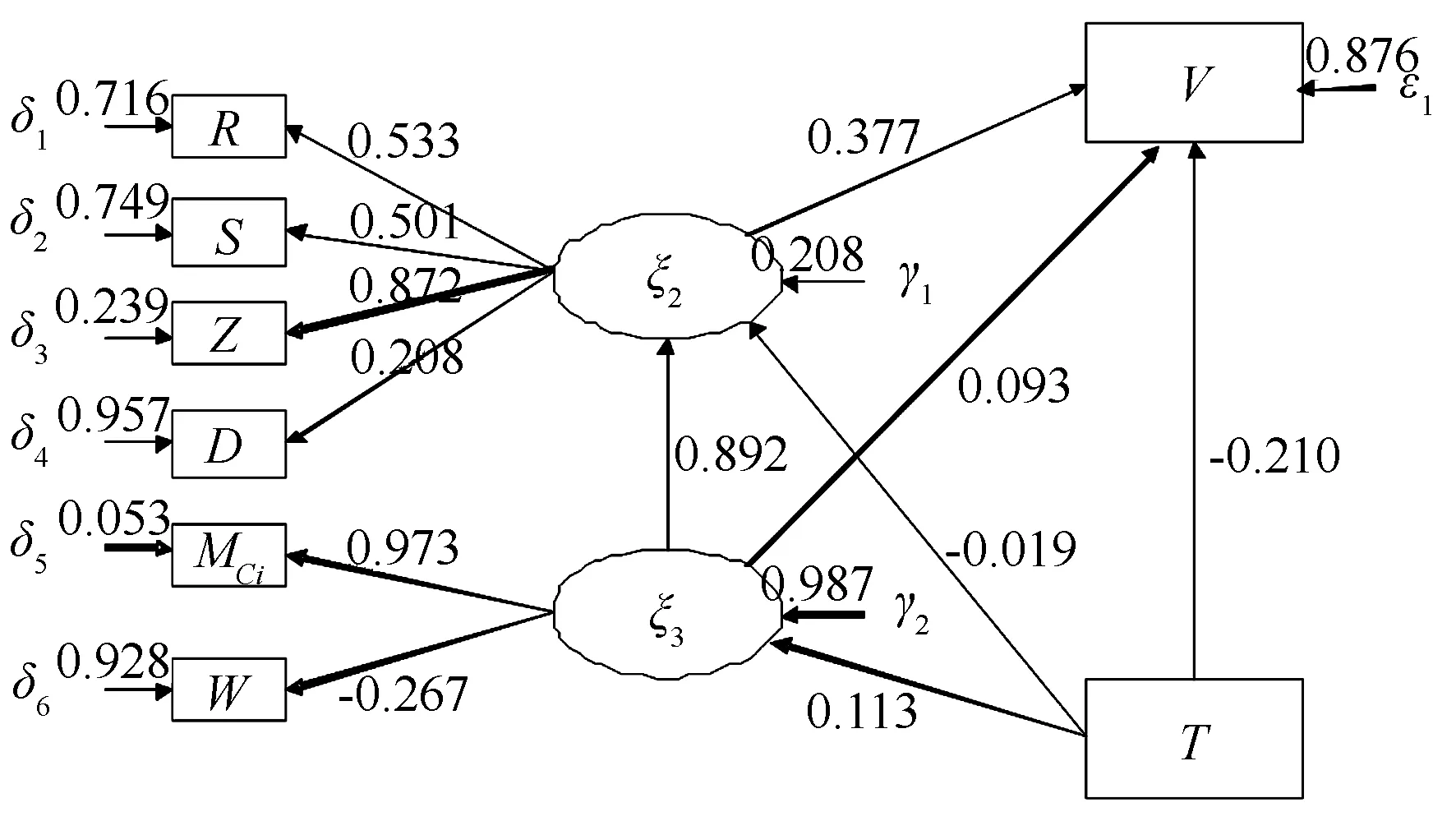
D為平均胸徑，Z為樹種組成指數，R為更新豐富度，S為Simpson指數，MCi為全混交度，W為角尺度，V為林分單位蓄積，δ、ε為測量誤差，γ為殘差值。

表5 模型2參數顯著性估計

模型2中，撫育強度(T)與林分非空間結構(ξ2)的相關系數為-0.019，表明撫育強度與林分非空間結構呈負相關；撫育強度(T)與林分空間結構(ξ3)的相關系數為0.113，表明撫育強度與林分空間結構呈正相關，且撫育強度對林分空間結構的影響大于對林分非空間結構的影響；撫育強度(T)與林分單位蓄積(V)的相關系數為-0.210，表明撫育強度與林分單位蓄積呈負相關，與模型1結果相同；林分非空間結構(ξ2)、林分空間結構(ξ3)，兩者與林分單位蓄積(V)相關系數分別為0.377、0.093，均呈正相關，且林分非空間結構對林分單位蓄積的影響大于林分空間結構對林分單位蓄積的影響。林分空間結構(ξ3)與林分非空間結構(ξ2)的相關系數為0.892，表明林分空間結構與非空間結構呈正相關。

4 討論

撫育采伐能夠優化林分結構。模型1中，撫育強度與林分結構呈正相關(0.108)，即隨著撫育強度的提高，林分結構趨于優化。模型2中，撫育強度與林分非空間結構為負相關關系(-0.019)，是由于撫育采伐對于林分物種多樣性的影響并不大；有研究認為，物種的數量隨間伐強度的增加而沒有出現顯著的變化[27]，還有一些研究認為，撫育采伐會產生人為干擾，不同物種之間競爭越發激烈，導致林分更新多樣性降低[3]。撫育強度與林分空間結構為正相關關系(0.113)，這與許多研究結果一致[28-29]；撫育采伐會促進林分空間結構的優化，降低林分空間結構異質性，提高林分樹種混交度的同時，降低林分角尺度，使得林木個體空間分布趨向隨機分布，林木個體獲得更大的生存及營養空間。撫育強度對林分空間結構的影響，大于對林分非空間結構的影響，這是由于林分空間結構指標均與林分內林木個體的空間分布有關，撫育采伐會減少林分內林木數量，改變林分內林木個體空間分布，因此會更直接地對林分空間結構產生影響。

撫育采伐會降低林分蓄積量。模型1、模型2中，撫育強度與林分單位蓄積之間的相關系數分別呈顯著負相關(-0.221、-0.210)，盡管撫育采伐優化了林分結構，但同時也使得林木株數急劇減少，林分恢復生長的時間又較長，使林分單位蓄積降低。有研究發現，雖然間伐可以顯著促進林木單株材積的增長，間伐強度不能有效增加林分活立木材積和林分出材量[30]。還有研究認為，撫育采伐是否能夠提高林分撫育采伐生產力還有待研究[31]。另外，撫育采伐對林分蓄積量的影響還可能受到立地條件、樹種類別、間伐方式等條件的制約，需要進行后續的研究。

林分結構的優化對林分蓄積量具有正向作用。采伐后林木株數減少，調整林分密度，擴大林木個體生存空間，林木間競爭減少，使林木能更好地獲取養分及光照等，這同樣也說明林分空間結構對林分非空間結構是具有正向作用的。有研究發現，進行過撫育采伐的樣地林分平均胸徑，大于對照樣地林分平均胸徑，且隨著間伐強度增大而增加，林分平均樹高也有所增加[30]。

本研究并未刪除不具統計學意義的影響因素(p>0.05)，模型構建應是理論驅動與數據驅動的結合，應在前人研究及理論基礎上建立，本模型雖然并不是統計學意義上的最優模型，但相對最優模型，本模型具有較多的實際意義。結構方程模型在林業領域的研究與應用較少，如何更加科學合理將結構方程模型應用到林業領域內，還需進一步的探討及驗證。

5 結論

本研究構建撫育采伐與林分結構、林分蓄積的結構方程模型，模型擬合結果可接受。模型結果表明，撫育采伐對林分結構具有正向作用(0.108)，且對林分非空間結構的影響(0.019)，小于對空間結構的影響(0.113)。撫育采伐對林分蓄積具有負向作用(模型1為-0.221、模型2為-0.210)，林分結構對林分蓄積具有正向作用(0.285)，林分空間結構對林分非空間結構具有正向作用(0.892)。撫育采伐對林分結構中非空間結構方面具有負向作用(-0.019)，因此，建議在進行森林撫育經營，優化林分空間結構的同時，重視對林分非空間結構的優化及調整。