多種組合模型的區域滑坡易發性及精度評價

楊 強，王高峰，丁偉翠，李榮建，高幼龍，鄧 兵

(1.西安理工大學巖土工程研究所，陜西 西安 404100； 2.中國地質環境監測院， 北京 100081；3.中國地質調查局 水文地質環境地質調查中心，河北 保定 071051； 4.中國地質科學院，北京 100037)

滑坡易發性是自20世紀90年代以來地質災害領域的研究熱點之一，并已成為世界各國防災減災戰略體系的重要組成部分，在開展城鎮規劃建設、地質災害風險管理和預警預報等方面取得了較好的應用效果。從研究區域可見我國在滑坡易發性評價研究主要分布在三峽庫區、汶川地震區及西北黃土區等西部山區，并形成了較為詳細的評價方法體系[1-3]。有學者針對白龍江流域開展了滑坡、泥石流發育環境、危險性評價等方面的研究[4-7]，研究對象多集中在白龍江干流或中游某一重要區段或國道212沿線。而關于整個流域尺度(甘肅段)的滑坡易發性評價研究甚少，目前仍然缺乏區域性國土空間用途管制規劃必需的滑坡災害易發性分區成果地圖，特別是針對評價模型的適用性和精度評價方法的對比研究鮮有案例。

滑坡易發性是指一定區域內由孕災地質條件控制的滑坡發生的可能性，而滑坡易發性不同于危險性，不考慮地震、降水等誘發因素。目前，區域滑坡災害易發性評價主要依靠啟發式推斷法、數理統計分析法和非線性方法等，后兩類評價方法具有運算效率高和因子權重易于客觀獲取的優勢而被廣泛運用[8]。其中，數理統計分析法包括基于原始數據，對其規律進行基礎處理的信息量模型、確定性系數模型、證據權法模型等[9-12]，非線性方法包括基于人工智能學習的人工神經網絡模型、決策樹模型、支持向量機模型及邏輯回歸模型等[13-14]。但由于單一的評價模型方法存在對參評因子不能客觀地確定其權重、模型運算過程中因主觀干擾而無法消除評價因子之間的相關性等問題，難以客觀、準確、定量地進行區域滑坡災害易發性評價。為獲得切合實際的評價結果，有學者開展了多種模型組合對滑坡易發性進行評價，總結分析了模型的優劣[15-16]。此外，評價因子選取不當或彼此相關性強或個數較多，及評價因子狀態分級方面客觀性影響較高，沒有科學合理的劃分依據，評價過程過于繁瑣，而且會影響模型評價結果的合理性和準確性。然而在評價結果分析方面很少有人關注這些評價模型和方法評價精度的對比與檢驗，事實上評價結果的準確性、分析精度及與實際情況的吻合程度是使用者最關注的問題，在數據有限條件下的評價結果更需要對精度進行分析。

本文在研究白龍江流域滑坡發育特征及孕災環境的基礎上，結合數據源的可獲取性，選取了坡度、坡高、距斷層距離、地層巖性、流域溝壑密度、歸一化植被指數(NDVI)等6個影響滑坡災害發生的致災因素作為參評因子。首先，結合2 093處滑坡災害及隱患點數據，并依據各指標條件下的信息量值、確定性系數值和證據權重值曲線突變規律、滑坡面積及分級面積頻率比曲線對各評價因子的狀態進行分級。然后通過應用信息量模型、確定性系數模型和證據權模型分別與邏輯回歸模型進行滑坡易發性評價。最后采用4種不同方法進一步檢驗評價結果的合理性，來開展研究區滑坡災害易發性及結果精度評價分析。力求從模型適用性和預測精度2方面選擇適合于該流域的最優滑坡易發性評價方法，真實地反映出滑坡易發性的空間分布特征，以期為地質災害突發、高發、頻發的白龍江流域地質災害防災減災預警決策提供參考。

1 研究區及數據源

1.1 研究區概況

根據甘肅省白龍江流域滑坡發育特征及現有滑坡災害數據，選取白龍江流域受滑坡災害影響最嚴重的白龍江中游及岷江支流段作為本文的研究區域。地理范圍在103°42′55.1″E～105°19′00.7″E，33°01′17.5″N～34°22′37.6″N之間，面積約6 128 km2，圖1為研究區地理概況及位置示意圖。

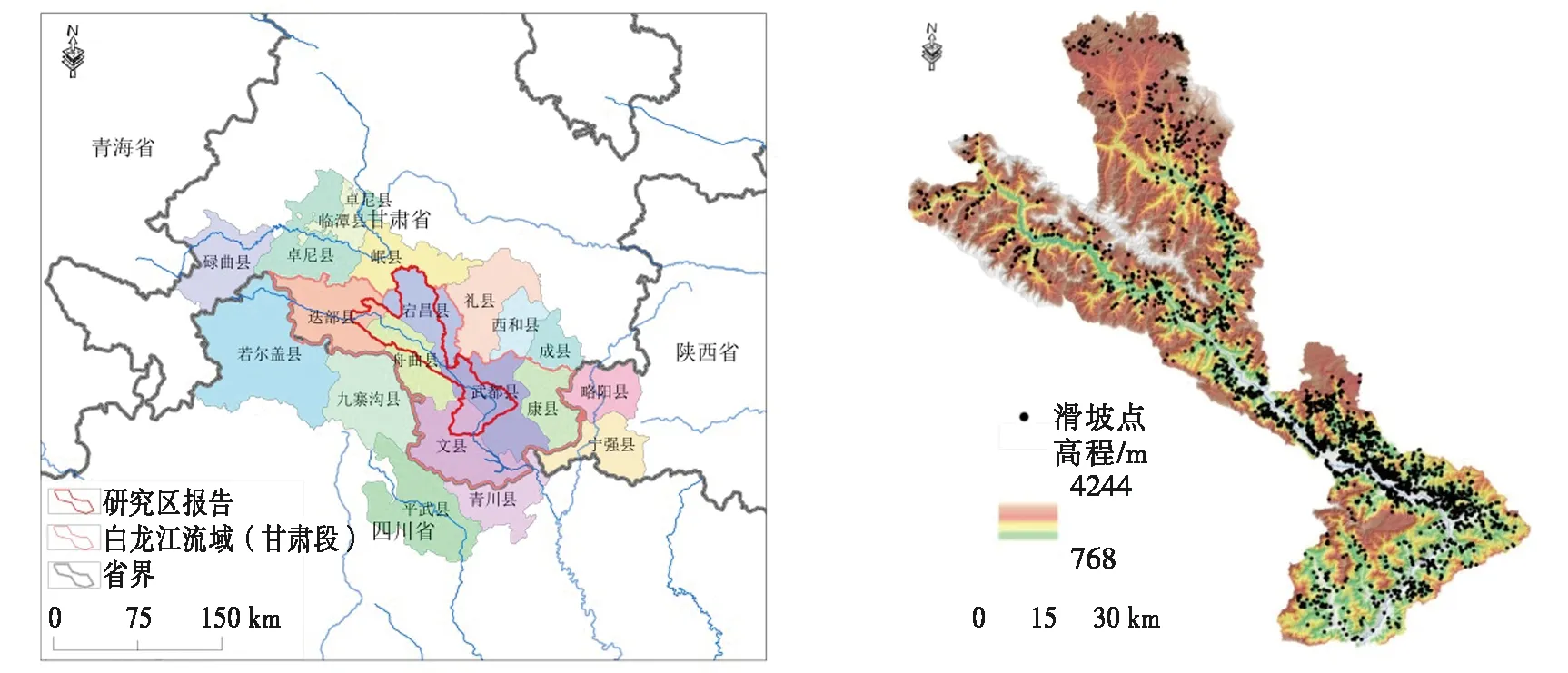
圖1 研究區位置示意圖Fig.1 Schematic diagram of study area location

該區位于青藏高原東部、秦嶺山地西緣，我國縱橫向地震帶在此交匯穿過，地質構造復雜，發育一系列活動的逆沖斷裂和走滑斷裂，且局部次級斷裂和小型褶皺集中發育，新構造運動強烈和地震活動頻繁。該區滑坡災害密布于軟弱淺變質巖地層區，尤其在分布有志留系、泥盆系等軟弱千枚巖區域最為突出，滑坡災害密度達0.48個/km2，是區內滑坡災害易發多發巖組。白龍江中游及其岷江支流貫穿整個區域，地貌類型復雜，屬中深切割中高山地貌區，地形海拔高度范圍為768～4 244 m，相對高差3 476 m。該區屬于亞熱帶向北溫帶的過渡區，氣候垂向上隨海拔變化具有差異性，在時空分布上降水分布不均勻[17]。受以上條件的影響使得該區地質災害發生的頻率高、規模大、種類多、范圍廣，且具有“群發性、突發性、隱蔽性、疊加性”的特點，每年造成的經濟損失巨大，其中滑坡災害的嚴重性亦是眾所周知，如鎖兒頭滑坡、泄流坡滑坡、江頂崖滑坡等。

1.2 數據源

本文開展滑坡易發性評價的數據源主要包括：(1)滑坡災害點的基礎數據主要來自隴南白龍江流域地質災害調查成果數據；(2)研究區1∶50 000地形圖和30 m×30 m分辨率DEM數據，用于提取坡度、坡高、流域溝壑密度等信息；(3)1∶100 000構造地質圖，用于提取地層、距斷層距離等信息；(4)2016年獲取的精度為0.5 m的Pléiades衛星遙感數據和2014年30 m×30 m的landsat8 OLI，用于提取歸一化植被指數。

研究區滑坡共2 093處，總面積224.54 km2，約占整個研究區面積的3.66 %。圖2為根據野外調查和已有滑坡資料整理得到的白龍江中游段滑坡發育面積分布曲線圖。可以看出：滑坡面積與滑坡分布個數呈雙峰曲線規律，整體上滑坡面積越大，分布個數越少。研究區最大滑坡面積為4.36 km2，最小為210 m2，在滑坡面積為0.001～0.015 km2和0.035～0.153 km2范圍內滑坡共有1 258處，占研究區滑坡總數和滑坡總面積的比例分別為60.11 %和25.64 %。

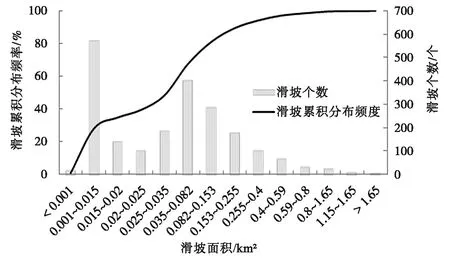
圖2 滑坡發育面積分布曲線Fig.2 Distribution curve of landslide development area

2 評價模型

目前較為常用的滑坡易發性評價模型均具有各自的優點和不足。信息量模型是采用條件概率的統計分析方法獲取評價因子的權重值，一定程度減小主觀因素的影響，也是目前國內地質災害易發性評價的通用模型，但不能反映不同評價因子對滑坡發生的貢獻權重或影響程度的差異。確定性系數模型計算過程嚴密，既能解決多層數據類型的歸并，又能較好地解決評價因子之間不同特征分級對滑坡易發性的影響，但未能體現各評價因子對滑坡易發性的差異性。證據權模型對評價因子個數無要求，但各評價因子之間需滿足獨立性檢驗，且要求滑坡樣本數據足夠多。邏輯回歸模型能用簡單的線性回歸來描述滑坡致災因子之間復雜的非線性關系，且計算便捷，對多層數據類型的合并卻無法解決。本文獲取的滑坡樣本數據詳實，評價因子基礎數據易獲得且精度較高，在基于數理統計進行易發性評價時可取得較理想的結果[18]。但滑坡災害孕育過程是一個非線性系統，線性的數理統計很難精確地對其進行預測。為了提升評估成功率或準確性，可綜合各自模型的優點對研究區的滑坡易發性進行建模，不僅能在GIS平臺的支持下快速得出評價結果，而且較理想地解決采用單一模型在滑坡易發性評價中的不足，使評價結果更滿足實踐和應用需求。

2.1 信息量模型

信息量模型是以信息論和工程地質類比法為理論依據。通過對歷史滑坡災害樣本數據統計，分析孕災地質環境與其時空分布關系，來獲取滑坡災害發育規律，從而推算出不同工程地質環境對滑坡孕育和產生的影響程度，其作用大小用“信息量”來衡量，其值越大，滑坡易發性越高，其公式如下：

(1)

式中，y為滑坡事件；xi(i=1,2,…n)為不同影響因子，n為影響因子個數；I(y,x1x2…xn)為影響因子組合(x1x2…xn)對滑坡所起作用大小的信息量；P(y,x1x2…xn)為影響因子組合下滑坡發生的概率；P(y)為滑坡發生的概率。

2.2 確定性系數模型

確定性系數模型是由Buchanan和Shortliffe提出一種概率函數方法[19]。利用確定性系數進行滑坡災害的易發性評價可以根據已發生滑坡災害與影響因子數據集之間的統計關系進行確定獲取，計算公式為：

(2)

式中：CF為滑坡發生的確定性系數；PPa為滑坡影響因子分類a中包含的滑坡災害個數與數據分類a面積的比值；PPs為整個研究區內滑坡發生個數與研究區總面積的比值。由式(2)可知CF的值域是[-1，1]，CF值為正值代表滑坡變形失穩的確定性高，表明孕災地質環境易于發生滑坡災害；CF值為負值代表滑坡變形失穩的確定性低，表明孕災地質環境不易發生滑坡災害。

2.3 證據權模型

證據權法是以貝葉斯雙變量統計模型為基礎的，綜合各種證據來證明一種假設的定量方法。通過對已知滑坡與其孕災地質環境因子進行空間關聯分析，計算影響因子中不同等級區間對滑坡事件的貢獻權重值，得到滑坡易發性指數，該指數的高低代表研究區發生滑坡可能性的大小。當各評價因子之間滿足獨立性假設，其公式如下：

Wf=W+-W-.

(3)

式中：W+表示影響因子分布區的正相關權重值；W-表示影響因子分布區的負相關權重值，如果W+<0或W->0時，影響因子與滑坡事件呈負相關，如果W+>0或W-<0時，影響因子與滑坡事件呈正相關，如果W+=0或W-=0是，影響因子與滑坡事件不相關；Wf為綜合權重，來表示該影響因子等級對滑坡變形失穩的影響權重值。

2.4 邏輯回歸模型

邏輯回歸模型是研究二值分類因變量與其多個互不相關的自變量之間關系的多元回歸統計分析方法，在滑坡災害分析中，它能較好地解決滑坡易發性評價出現的二分類因變量的問題(1代表發生，0代表未發生)。設某滑坡事件發生的概率為P，不發生的概率為1-P，x1x2…xn表示滑坡發生的n個評價因子，其發生和未發生概率可用Logistic回歸函數公式表示為：

P=eβ0+β0x1+…+βnxn/(1+eβ0+β0x1+…+βnxn).

(4)

該模型中β0為截距，βi為回歸系數，即反映的是滑坡不同影響因子的相對貢獻大小。模型輸出結果P的范圍為[0，1]，1表示滑坡發生的概率為100%，0表示滑坡發生的概率為0%。對式(4)兩邊取自然對數，進行Logit轉換，并作為因變量，將評價因子xi(i=1,2,…n)作為自變量，建立線性回歸方程：

.

(5)

式中P值反映了在影響因子x1x2…xn的共同作用下，滑坡的發生的可能性大小和敏感程度。

2.5 多種組合模型

將信息量模型、確定性系數模型和證據權模型計算出的各個評價因子等級的I值、CF值和Wf值作為邏輯回歸模型中的指標值，構建不同組合回歸方程，得出邏輯回歸系數βi，以此為依據開展研究區滑坡易發性評價。

因此本文隨機選取滑坡災害點總樣本的80%作為訓練樣本(即1 680個發生滑坡災害點)進行建模分析，相應的隨機選取1 680個未發生滑坡的樣本點，共計得到3 360個具有獨立屬性的樣本數據，并將其作為因變量樣本集。結合評價因子，分別采用信息量模型I+邏輯回歸模型LR(組合1)、確定性系數模型CF+邏輯回歸模型LR(組合2)和證據權模型WF+邏輯回歸模型LR(組合3)3種組合模型評價研究區的滑坡災害易發性并進行分區，分析3種組合模型得到的研究區滑坡易發性評價結果。利用20%的滑坡樣本點，采用多種方法檢驗評價結果的合理性，結合滑坡實際分布規律及發育情況討論并比較3種組合模型的適用性和準確性。

3 評價因子的選取與狀態分級

3.1 因子提取

滑坡的發生是孕災環境因子和誘發環境條件共同作用的結果，其中孕災環境因子是指斜坡自身的屬性特征，在經過剝蝕或風化等作用逐漸使斜坡趨于變形失穩狀態。誘發環境因子是指在降雨、地震、人類工程擾動等影響下導致斜坡失穩的外界條件。通常，滑坡易發性評價主要考慮對滑坡發生發展起控制性作用的孕災環境因子，來揭示斜坡未受外界條件影響工況下的失穩概率。促使滑坡產生的孕災環境因子主要包含：地形地貌、基礎地質、地表覆被和水文環境因子等4大類。在評價因子的選取中既要合理靈活又要體現因子對滑坡的影響，同時要確保各因子之間互不影響且不具有強相關性。因此，本文基于野外實地調查及收集到的數據庫與前人研究成果，選取坡高、坡度、地層巖性、距斷層距離、溝壑密度、歸一化植被指數(NDVI)等6個孕災環境因子，采用30 m×30 m分辨率的柵格單元作為研究區滑坡易發性的基本評價單元，在此基礎上進行滑坡指標因子的狀態分級及易發性評價。

3.2 影響因子狀態分級

影響指標因子狀態分級是指數據類型為離散型和連續型的單因子指標遵循一定的劃分標準分為多個不同范圍的二級狀態。其中離散型數據主要根據野外調查滑坡孕災工程地質條件類比制定劃分標準。而連續型數據是以一定步長的因子信息與預測單元個數分布曲線和綜合式(1)、式(2)及式(3)計算各步長在各因子中的I值、CF值、Wf值分布曲線為依據。對比2類曲線的分布規律，確定分布曲線的突變點為等級劃分的界限值，突變點范圍內的數值不僅體現了預測單元空間上的各等級之間的差異性，也體現了評價單元預測的相對集中性。

3.2.1 地形地貌因子

本文地形地貌因子主要包括坡高、坡度，均是應用ArcGIS的空間分析工具從DEM中提取的柵格數據。統計坡高、坡度2個影響因子不同區間內的滑坡面積比和分級面積比，如圖3所示，可以看出發生滑坡的坡度主要集中在[25°，45°]區間，研究區坡度從15°到40°內的面積最大，且在[10°，35°]區間滑坡面積比大于分級面積比，表明滑坡的相對面密度較大。坡高在100～200 m范圍時滑坡發育較多，在75～175 m區間對滑坡影響較大。

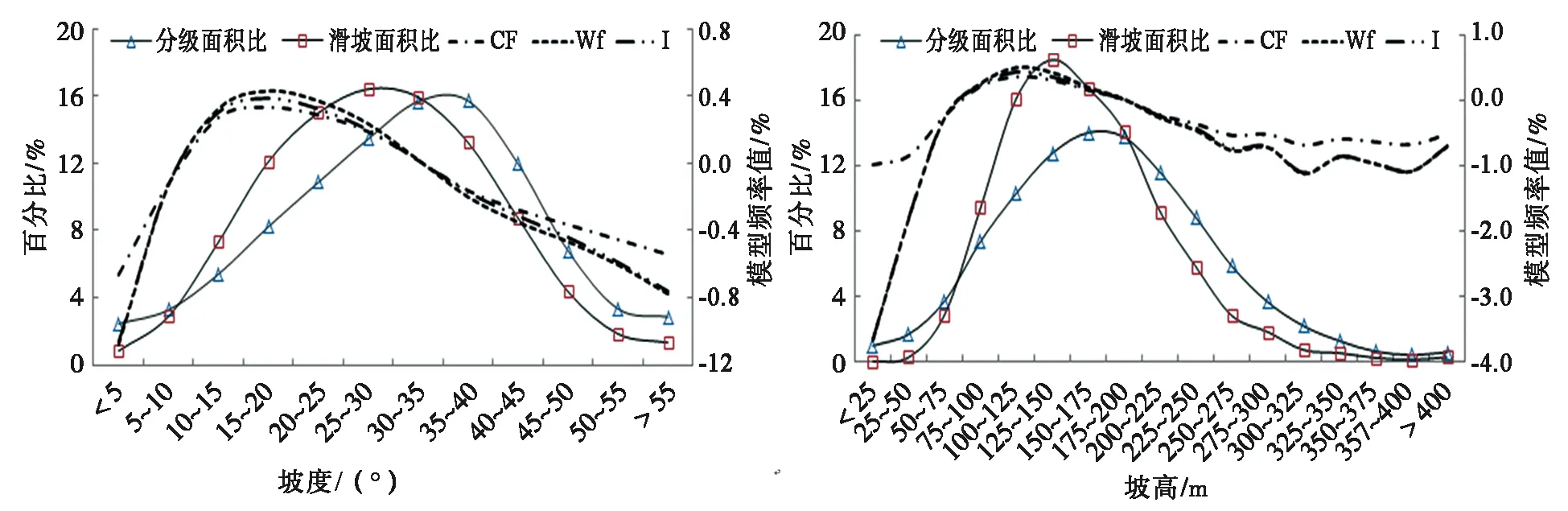
圖3 地形地貌因子狀態分級統計圖Fig.3 Classification statistical map of topographic and geomorphic factors

3.2.2 水文環境和地表覆被因子

(1)水文環境因子

流域溝壑在一定程度上反映了該地區地形切割程度、起伏程度和巖土體松散程度，亦能反映土壤侵蝕的嚴重程度，也能反映地貌的演化階段。通常水系發育程度和分布密度越高對地表侵蝕能力就越強，就越易于發生地質災害。在對區域滑坡易發性評價研究中，很難揭示地下水對斜坡的穩定性的影響，因此，本文以任一單元內溝壑密度大小來表達水系對區域滑坡發育的影響。

根據研究區DEM數據提取出的水系分布圖，采用ArcGIS的空間分析工具，制作研究區流域溝壑密度柵格圖層，分別對其影響范圍內的滑坡頻率進行統計，結果如圖4所示。結果顯示隨著流域溝壑密度的增大，滑坡面積及滑坡災害點密度呈現先增大后急劇降低，最后以微弱趨勢遞減。這主要原因，一是隨著溝壑密度的增大，水土流失程度也隨之增強，導致坡體表面松散物質已全部滑移，大多數基巖出露；第二，當溝壑密度大于3.2 km/ km2時，其覆蓋區域主要分布于白龍江及岷江支流河谷地帶，零星發育小型河岸塌滑，滑坡基本不發育。故滑坡面積在0.8～1.6 km/km2范圍內相對較大，在([0.8，2.2]、[2.4，3.2])km/ km2區間對滑坡影響較大。根據曲線規律，將流域溝壑密度分為<0.8km/ km2、0.8～1.2 km/ km2、1.2～2.4 km/ km2、2.4～3.2 km/ km2、3.2～3.489 km/ km2等5個狀態。

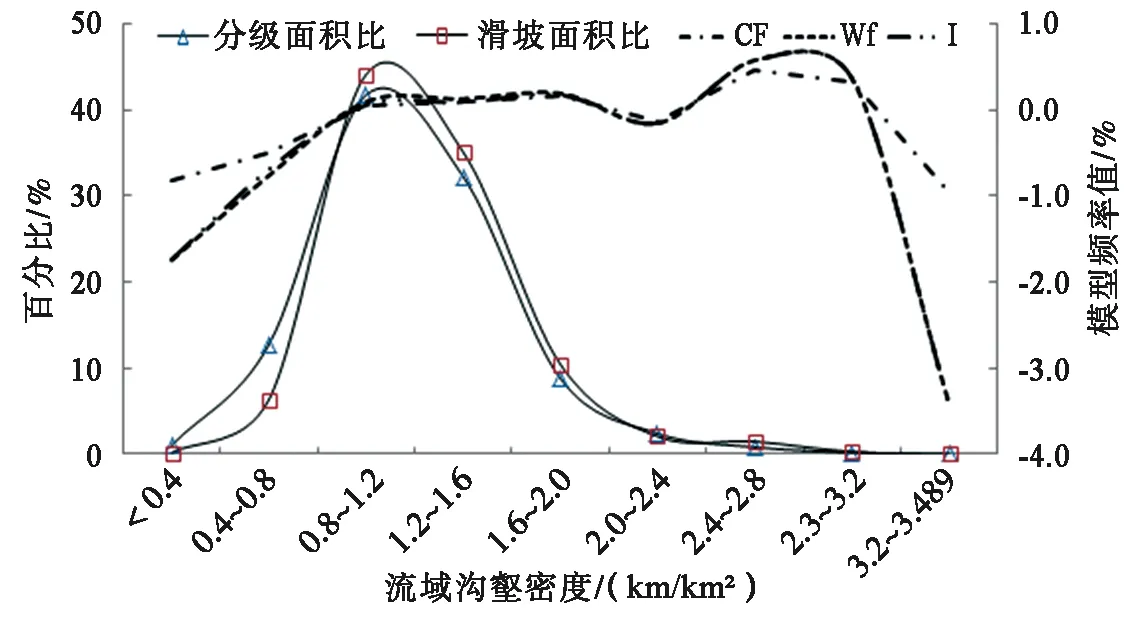
圖4 流域溝壑密度狀態分級統計圖Fig.4 Statistical map of gully density classification in river basin

(2)地表覆被因子

植被覆蓋度的變化主要影響地表水對巖土體的入滲侵蝕程度，造成斜坡穩定性降低，進而導致滑坡變形失穩概率增加，因此本文采用歸一化植被指數(NDVI)來表征地表覆被。

從圖5中滑坡面積比和分級面積比曲線可以看出，發生滑坡的NDVI主要集中在[0.25，0.40]區間，研究區NDVI從0.18到0.45內的面積最大，且在[0.10，0.35]區間滑坡面積比大于分級面積比。根據圖5模型頻率值曲線分析可知，隨著流NDVI的增大，滑坡面積呈現先急劇增大后逐漸較小的趨勢，NDVI在 [0.1，0.3]區間對滑坡影響最大。根據曲線規律，將NDVI分為<0.1、0.1～0.3、0.3～0.45、0.45～0.5、>0.5等5個狀態。圖6為連續型指標坡度、坡高、流域溝壑密度、植被歸一化指數(NDVI)因子狀態分級圖。

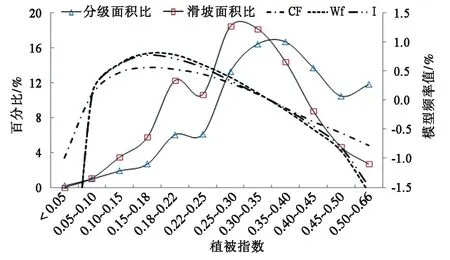
圖5 地表覆被狀態分級統計圖Fig.5 Statistical map of land cover classification

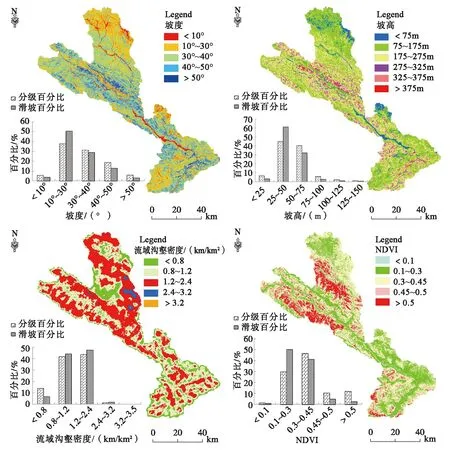
圖6 連續型因子狀態分級圖Fig.6 Continuous factor state grading chart

3.2.3 基礎地質因子

通常認為地層巖性與斷裂構造是影響滑坡孕育的兩個重要基礎地質因子。以往研究成果認為，白龍江流域滑坡主要沿斷裂帶成群成帶分布，在沿區域性活動斷裂一般發育大型或巨型滑坡，據統計70.6%的滑坡分布在距斷裂2.5 km范圍內，在距離斷層小于5.0 km范圍分布有90%以上的大型滑坡[20-22]。而在地層巖性軟弱區或軟硬相間巖層區內滑坡成片發育，此次調查共有1132處滑坡發育于軟弱巖層區，441處滑坡發育于軟硬相間巖層區，占滑坡總數的75.2%。故選取巖性與構造活動作為滑坡易發性評價的基礎地質條件。

(1)地層巖性

地層對滑坡孕育起著重要的影響作用，主要是通過影響堆積體和基巖的物理力學性質及其滲透性來促使滑坡變形失穩，同時，它決定了滑坡發育的規模、類型特征。研究區地層巖性極為復雜，屬西秦嶺地層區，從前震旦系到第四系均有出露，共出露30套地層。

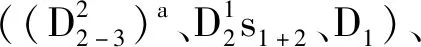
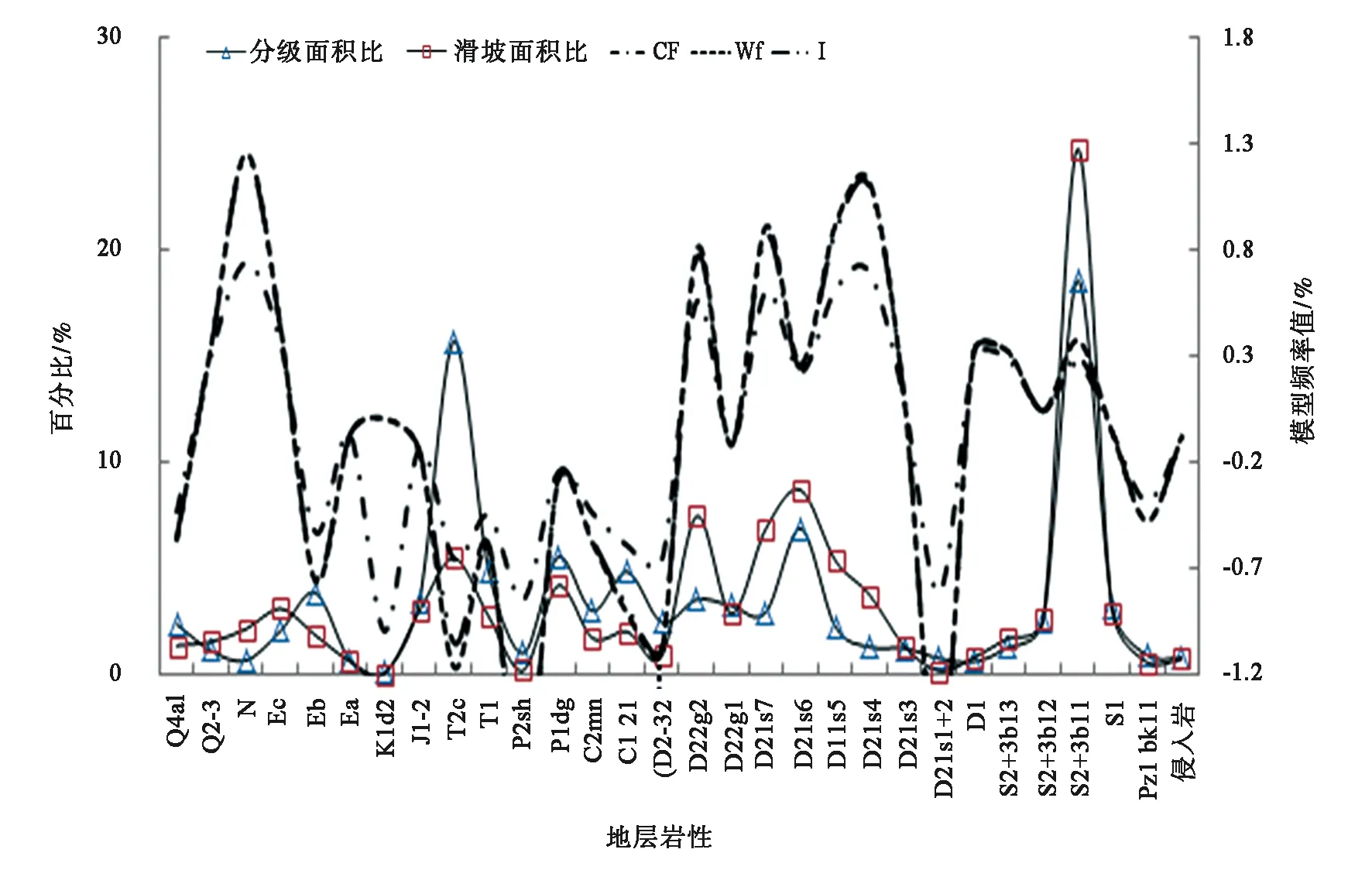
圖7 研究區控滑地層巖性因子狀態分級統計圖Fig.7 Statistical map of stratum lithology classification of slip-controlling strata

表1 研究區控滑地層巖性分級Table 1 Classification of stratum lithology

(2)地質構造條件

滑坡發育和發生與斷裂構造活動有著密切的關系，距斷層的距離是滑坡易發性分析的一個重要影響因子[23]。研究區滑坡的發育主要受到活動斷裂控制，最為典型的是坪定-化馬活動斷裂(帶)，沿該斷裂破碎帶發育一系列特大型滑坡，呈現出滑坡后壁至分水嶺的長條狀、“背滑”、“對滑”相間線狀分布特征，其物質結構、成分、成因復雜，次級斷裂發育。

研究區內滑坡沿斷裂呈帶狀分布的特征非常明顯，通過對區內滑坡的分布隨距斷層的距離統計表明：滑坡災害的分布隨其距斷層距離呈急劇衰減的趨勢，滑坡災害個數與斷裂的地表破裂面的垂直距離滿足以下關系：

N=1062e-0.365Dr(R2=0.8839).

(7)

圖8與式(7)說明研究區內滑坡分布與斷層有著顯著的關系，即：距斷層越近，斷層活動對斜坡的作用越強烈，就越容易誘發滑坡；反之，隨著距斷層距離增大，斷層活動對斜坡作用迅速減弱。在統計的2 093處滑坡中有1 220處分布在距斷層距離小于1.0 km范圍內，約占滑坡總數的58.29%。

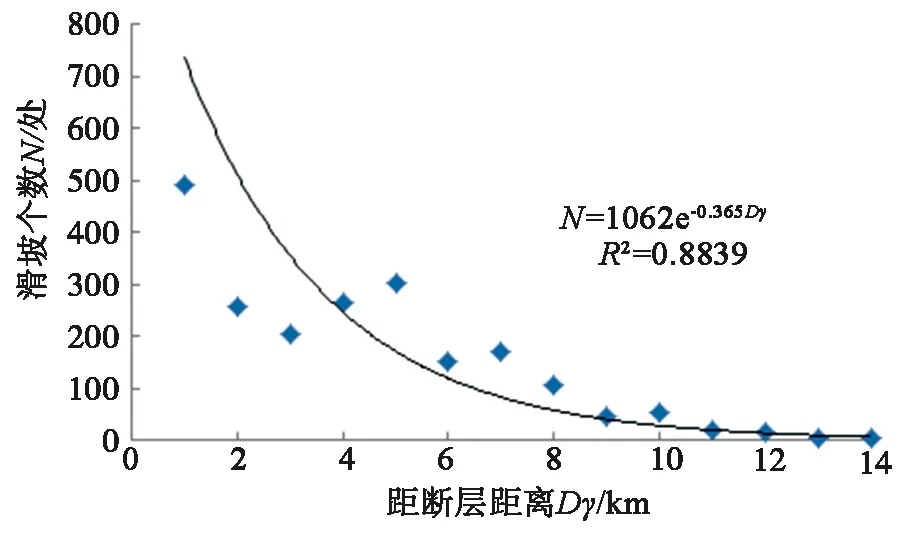
圖8 研究區滑坡個數與斷層距離關系圖Fig.8 The relation map of landslides amount and fault distance

通過對區內498條斷層，利用距斷層的歐氏距離來表示地質構造活動對滑坡的影響，分別對各緩沖區內的滑坡進行頻率統計，結果如圖9所示，可以得出在距斷層[0，1.0 km]區間滑坡面積比大于分級面積比，且滑坡主要發育在距斷層距離小于2.2 km范圍內。利用與地層巖性影響因子相同的分級方法將研究區斷層影響帶劃分為4個級別，因為在這4個構造影響帶之外仍有滑坡發育，故將該范圍定義為第5級影響帶，分級結果如表2所示。

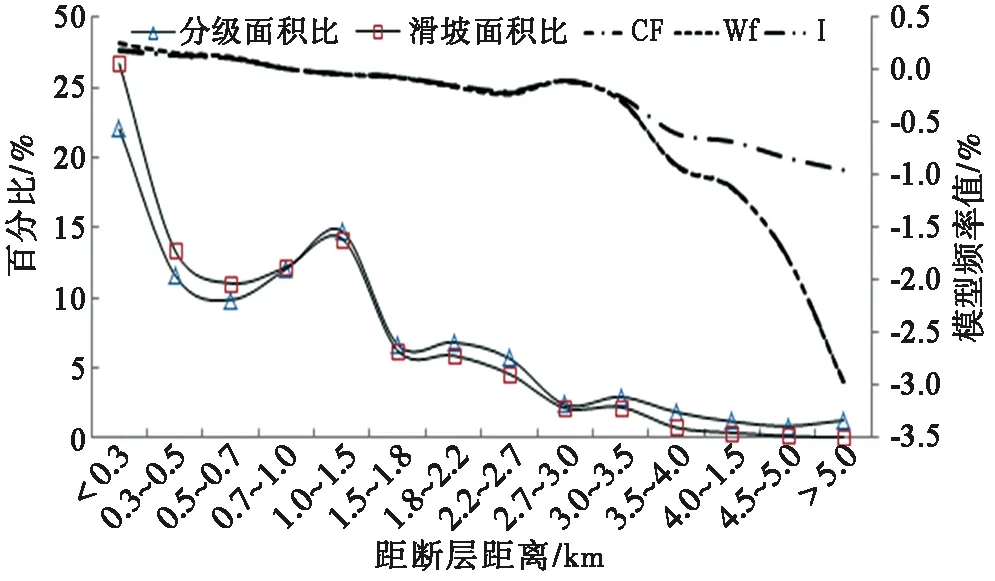
圖9 距斷層距離狀態分級統計圖Fig.9 Statistical map of the state classification of the distance from fault

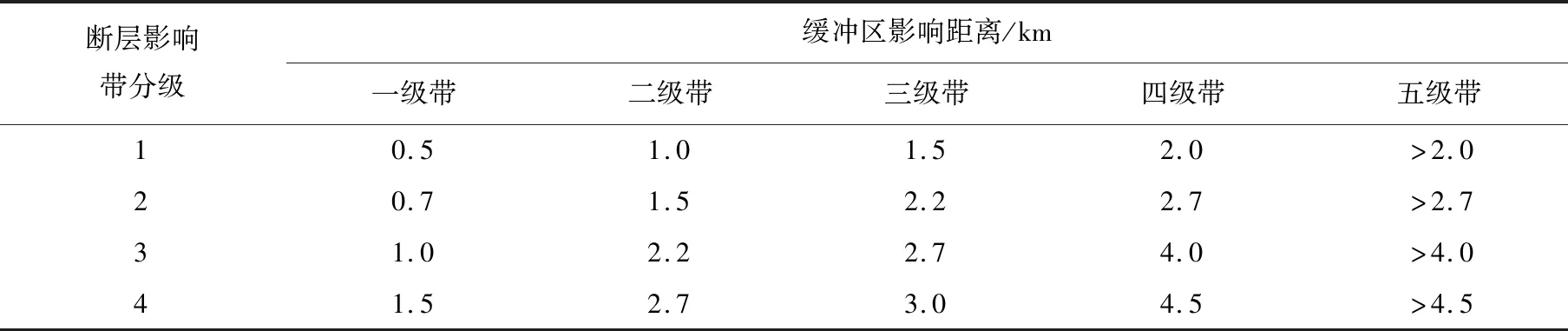
表2 研究區距斷層距離對滑坡發育影響分級統計Table 2 Classification statistics of the influence of fault distance on landslide development in study area

地層巖性、地質構造條件等屬于離散型指標，因子狀態分級結果如圖10所示。

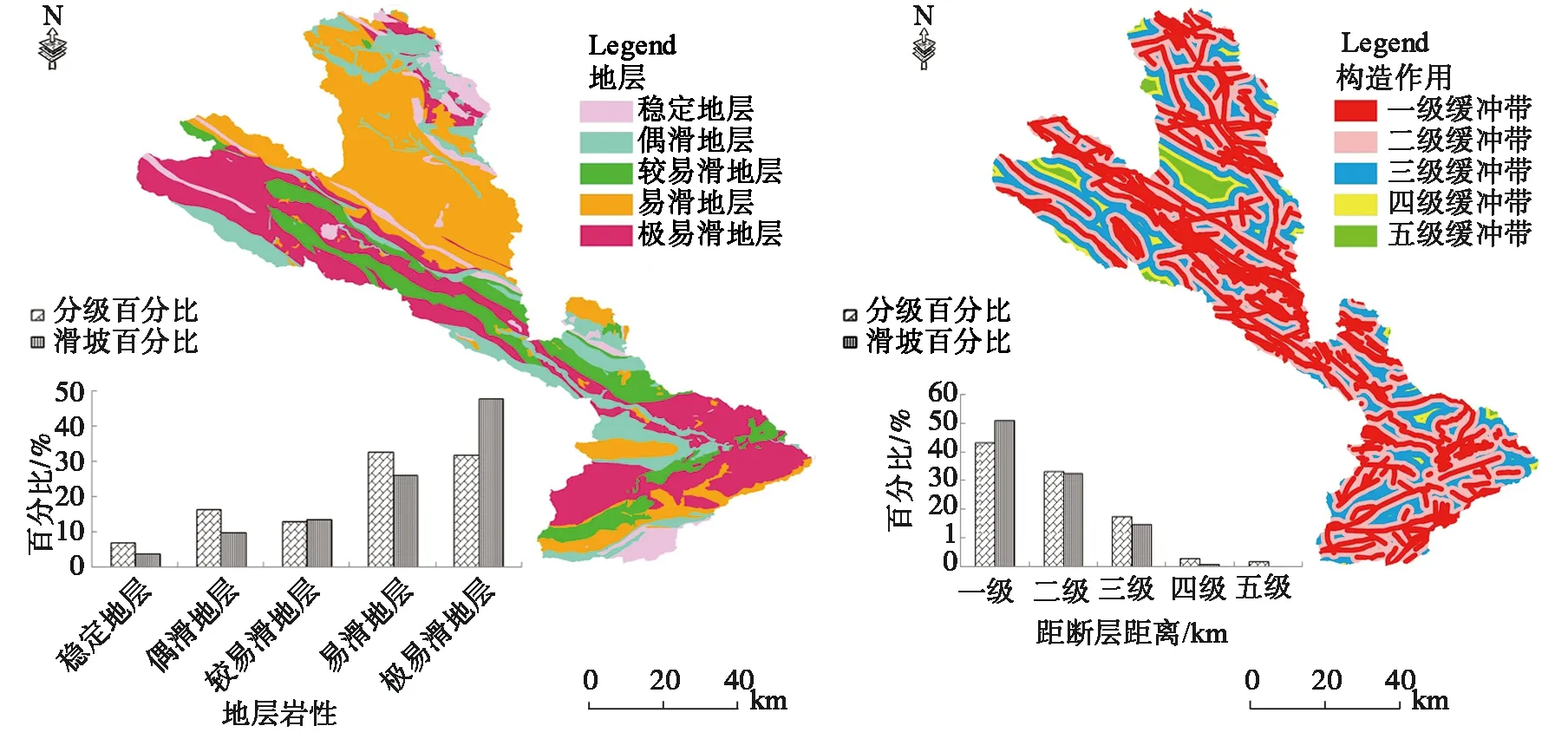
圖10 離散型因子狀態分級圖Fig.10 Discrete factor state classification diagram

3.3 評價因子I值、CF值和Wf值計算

首先，根據2 093個滑坡樣本點在各評價因子分級狀態中的分布情況，分別采用公式(1)～公式(3)計算各分類級別在各評價因子中的I值、CF值和Wf值，結果見表3。上述數值不僅可以進行各個評價因子的分類級別之間比較，而且可揭示同一評價因子內各分類級別的相對重要性。

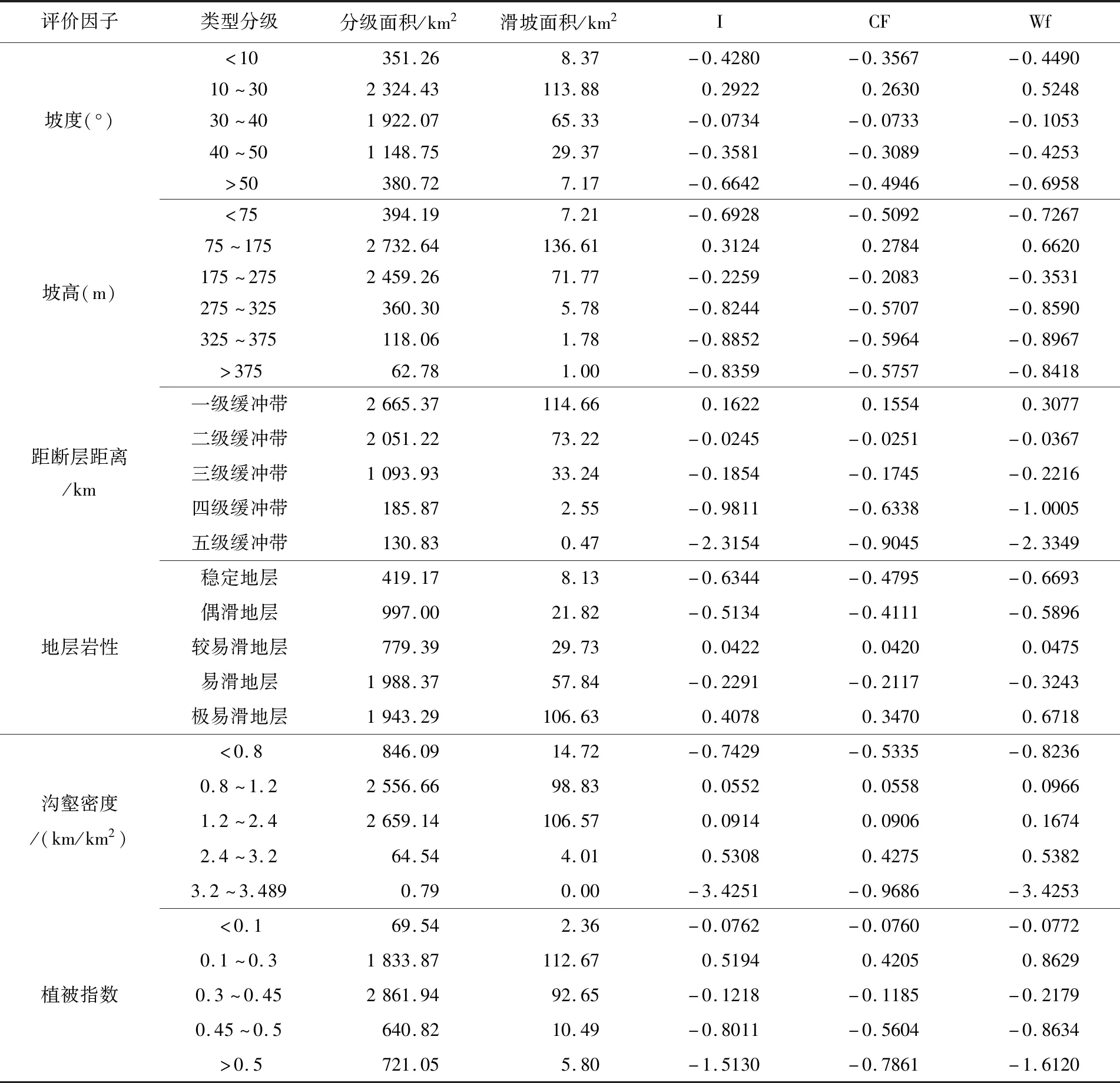
表3 各評價因子分類級別I值、CF值和Wf值計算結果Table 3 Calculation results of I Value、CF Value and WF Value for each evaluation factor classification level

3.4 評價因子共線性診斷

盡管基于工程地質類比法選定的影響因子能在一定程度上正確反映滑坡發育和因子的空間關系，但是受區域地質環境條件空間分布多樣性和差異性的影響，這些因子可能具有一定的相關性，彼此之間并不是完全相互獨立的。若因子之間存在高度的相關性或盲目選取更多的參評因子而不對其重疊性和共線性進行處理，會使模型評價結果失真或難以估計準確性。

因此，為了確保各參評因子互不影響和達到評價模型輸入參數準確性的要求，需對所選各指標因子進行篩選。本文首先選取滑坡災害點總樣本的80%(即1 680個發生滑坡點)和1 680個未發生滑坡的樣本點作為訓練樣本。然后提取每個樣本的各分級后因子等級值，采用SPSS軟件中進行多重共線性診斷，獲取其方差膨脹系數VIF和相關性系數R(表4)。表4計算結果顯示分級后確定的6個指標因子VIF值基本接近，表明因子之間存在共線性的可能性較小；同時各因子之間的相關矩陣R≤0.3，可認為所選各因子之間相關性微弱或不相關。因此這6個指標因子滿足相互獨立的要求，均可參與模型評價。

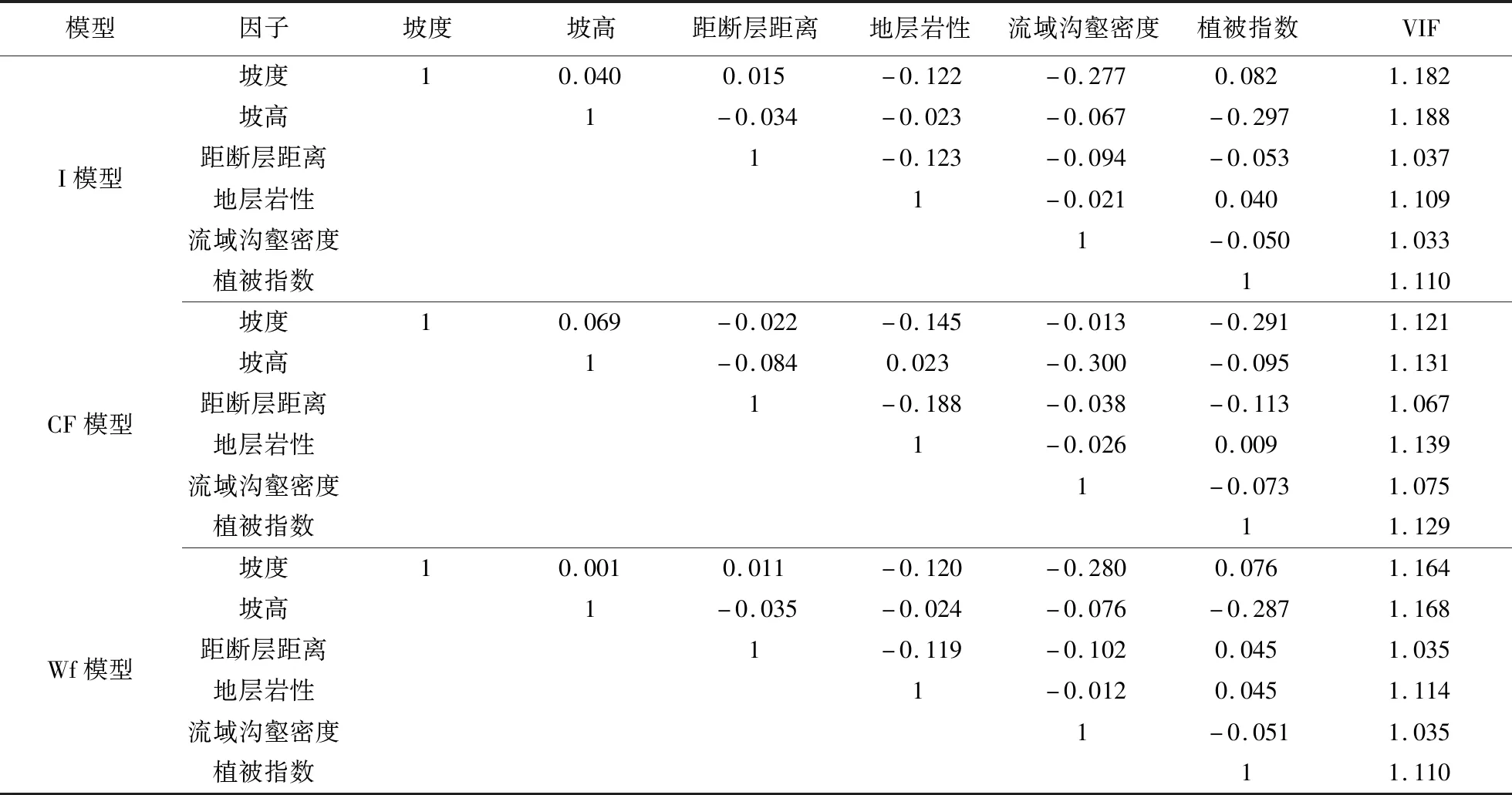
表4 評價因子的相關矩陣及VIF計算結果Table 4 Relevance matrix of evaluation factor and VIF calculation results

3.5 評價因子權重值計算

通過GIS分析計算工具中的柵格計算器將所得的各評價因子I值、CF值和Wf值賦予各圖層，獲得18張新的評價因子的模型值圖。然后提取3 360個訓練樣本各賦值后因子等級值作為自變量，是否發生滑坡災害作為因變量(0代表未發生滑坡災害，1代表滑坡災害點)，分別輸入SPSS軟件中進行多項邏輯回歸分析。把分析結果中得到的各因子的回歸系數B作為該因子的權重，各個變量在方程中的重要程度通過sig值(或wals值)來體現，sig值小者(或wals值大者)變量的顯著性就越高，在方程中貢獻就越大，當sig值小于0.05時才具有統計意義。

回歸結果顯示，3種組合模型計算出的各因子sig值均小于0.05(表5)，說明選取的6個因子都是有效的，同時各因子之間的相關系數都小于0.3，表明所選因子是合理的。組合1模型計算出的因子權重大小依次為植被指數、地層巖性、坡高、流域溝壑密度、坡度、距斷層距離；組合2模型計算出的因子權重大小依次為植被指數、地層巖性、坡高、坡度、流域溝壑密度、距斷層距離；組合3模型計算出的因子權重大小依次為植被指數、地層巖性、坡高、流域溝壑密度、坡度、距斷層距離。可見3種組合模型中各因子對模型貢獻大小變化很小。

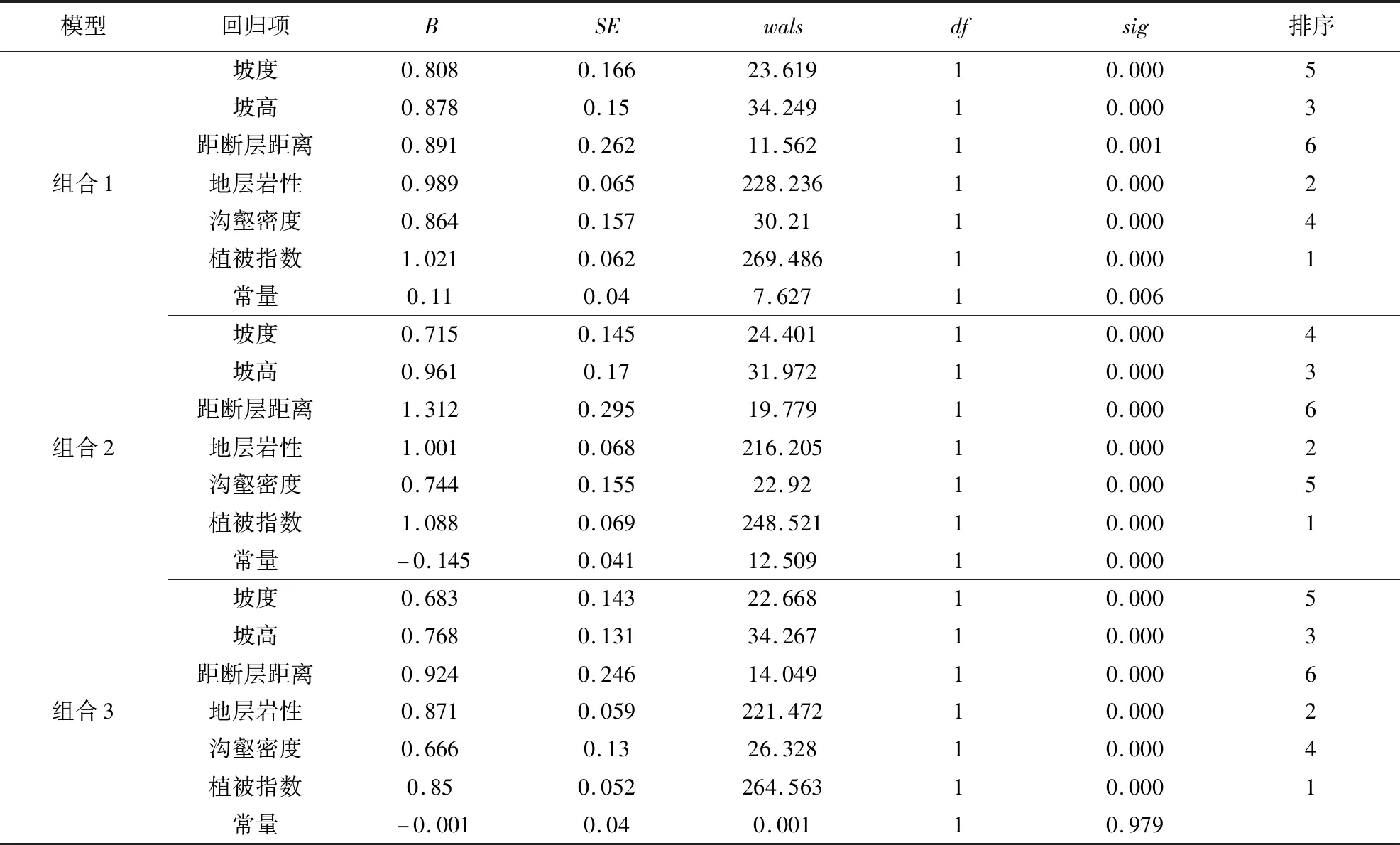
表5 3種不同模型邏輯回歸分析結果Table 5 Logical regression analysis results of the three models

4 評價結果分析及精度評價

4.1 易發性評價分區與評價結果

從各因子的回歸系數與不同組合模型得到的各分類級別的I值、CF值和Wf值乘積可以看出，結果均表現是在以千枚巖、炭質板巖為主的淺變質巖區、距離斷層1.5km內、流域溝壑密度在2.4～3.2 km/km2區段、坡度25～45°和坡高為75～175 m范圍內、植被裸露區即NDVI為0.1～0.3分布區最容易發生滑坡災害的地方。

在ArcGIS軟件中，根據3種組合得到的各因子回歸系數結合公式(4)～(5)計算出研究區滑坡災害發生的概率P，生成研究區滑坡發生概率分布圖，在此基礎上采用似然比模型對滑坡易發性概率結果按P值大小分為四類：低易發區(0～0.25)、中易發區(0.25～0.45)、高易發區(0.45～0.65)和極高易發區(0.65～1)，最終得到研究區滑坡易發性評價分區圖(圖11)。結合滑坡訓練樣本數據，統計各易發性等級區域內滑坡災害點個數(表6)顯示：組合1模型中，76.07%的滑坡災害落入高易發區和極高易發區，落入中易發以上的滑坡占滑坡總數的93.69%；而組合2模型和組合3模型滑坡災害點劃分到高易發以上區域的滑坡比例分別為73.33%、74.76%。大量的滑坡災害點集中發育在易發性較高的區域內，而易發性較低的區段滑坡發育相對較少，表明采用3種組合方法所得到的評價結果與實際滑坡災害點的分布情況基本吻合。

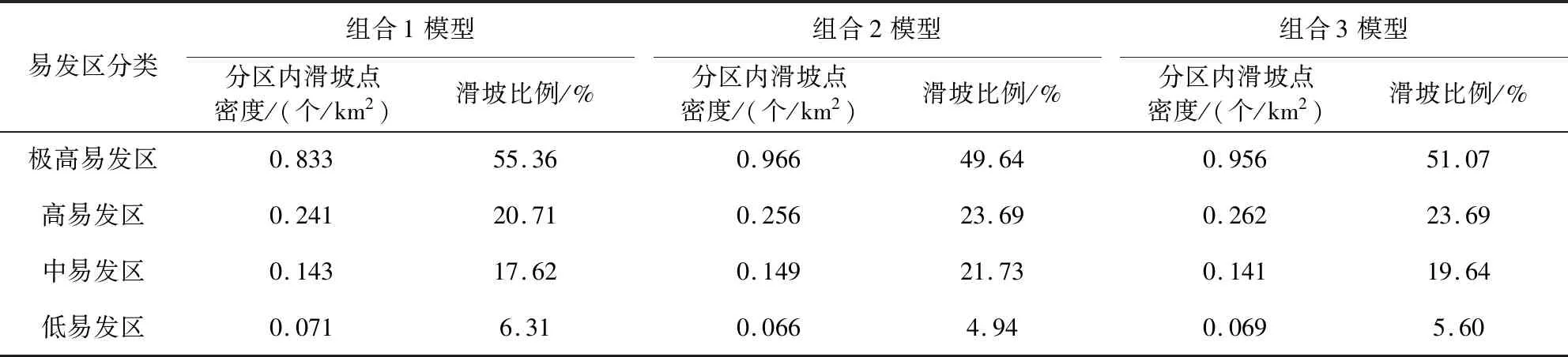
表6 不同模型易發性分區內滑坡點個數Table 6 The number of landslide points in the prone zones of different models

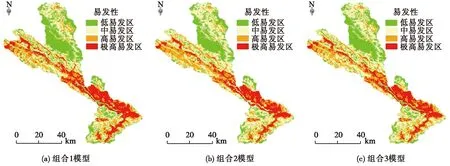
圖11 不同模型的易發性評價結果Fig.11 Susceptibility assessment results of different models

從圖11不同組合模型易發等級圖分布狀況來看，研究區滑坡極高易發區主要分布白龍江兩岸，尤其分布在兩河口至桔柑鄉段白龍江左岸區域。易發性高的區域滑坡分布有以下特征：1)沿活動性斷裂呈線狀分布，組合1模型較明顯地揭示坪定～化馬斷裂對滑坡發育的控制性作用，而在研究區南部滑坡集中分布在次級斷裂和小型褶皺密集區；2)受易滑地層控制明顯，易發程度極高的區域主要是由軟弱千枚巖、炭質板巖組成志留系1段地層及由灰巖、千枚巖互層構成泥盆系6、7段易滑地層區，該類巖組受內外營力影響強烈，在斷裂帶沿線或新構造運動活躍區域，常形成具有塑性流特性且厚度小于5m的淺層殘坡積堆積物斜坡，在降水的作用下易發生中小型滑坡；3)在流域溝壑密集區呈串珠狀連片分布；4)地表為基巖出露與裸土地帶且坡面侵蝕程度強的區域，滑坡集中分塊、分區發育。

4.2 精度評價

模型精度評價是檢驗評價結果精準性和合理性的重要手段。本文采用4種方法對不同組合模型進行精度評價，一是根據實際發生的滑坡災害點在各易發等級區間內的分布情況來檢驗其合理性；二是通過Sridevi Jadi經驗概率法[24]、Cohen′sKappa系數法[25]、ROC成功概率法對模型評價的精度進行檢驗。

(1)為了避免主觀因素影響，使得構建的不同組合模型具備良好的穩定性，選取未參與模型訓練的415個滑坡災害點(約占樣本總數的20%)作為預測樣本進行預測率檢驗。滑坡災害易發性評價結果的合理性需滿足2個檢驗準則：一是檢驗樣本點落在高易發區的百分比應最大和不易發區占整個研究區面積的百分比應該最小；二是檢驗樣本點落在各易發等級區的百分比和各等級區的面積占整個研究區的總面積的百分比的比值即頻率比應該隨易發區等級的增高而增大。從表7可以看出，3種組合模型計算結果都完全滿足上述2個準則，說明滑坡易發性程度劃分結果是合理的。

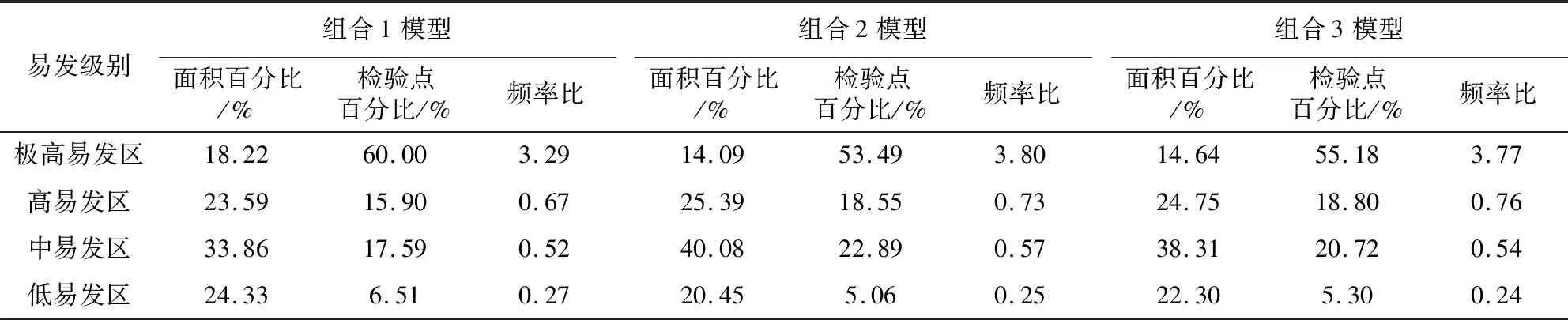
表7 不同模型易發性的檢驗結果對比Table 7 Comparison of susceptibility test results of different models

(2)Sridevi Jadi經驗概率法，是1997年由Sridevi Jadi提出的以經驗概率形式來表達精度評估的方法，屬于受臨界值約束的準確性統計方法，其臨界值不唯一，表達式為：

(8)

式中，N為評價單元總數；S為存在滑坡的單元總數；K是斜坡易發性為中等和高的單元總數；KS為存在滑坡的斜坡易發性為中、高的單元總數。

(3)Cohen′s Kappa系數法屬于典型的受臨界值約束的準確性統計方法且計算方法便捷，但臨界值的選取具有較大的隨意性和主觀性，定義式為：

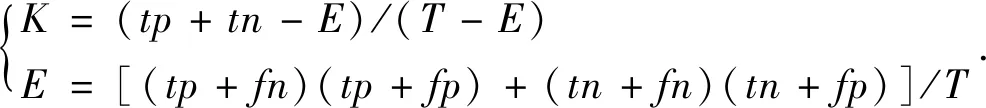
(9)

式中T為評價單元總數，其它各參數見表8，其中當為K>0.61精度較好的評價模型；0.41≤K≤0.60為中等評價模型；K<0.41為精度較差的評價模型[4]。

表8 滑坡模型評價列聯表Table 8 Contingency table of landslide model assessment

(4)ROC成功概率曲線法是區域地質災害易發性評價精度檢驗且不受臨界值約束的圖形化方法。可直觀準確地反映易發性從低到高，落在不同易發性區間內的滑坡數量(滑坡面積)的變化情況，其曲線下的面積AUC越大，表明模型成功率越高、預測效果越準確，具有很好的客觀性和有效性。

(5)評價結果檢驗。評價計算結果顯示組合1模型、組合2模型、組合3模型Kappa系數值分別為0.431、0.416、0.424。而運用Sridevi Jadi經驗概率法的3種模型的預測結果精度分別為57.39%、54.07%、56.11%。以發生滑坡數量被正確預測的比例-易發性指數比累積曲線下面積法對檢驗樣本的評價結果預測準確性進行檢驗，可得組合1模型、組合2模型、組合3模型的檢驗樣本的被正確預測的準確率AUC值分別為0.946、0.826、0.897(圖12)。

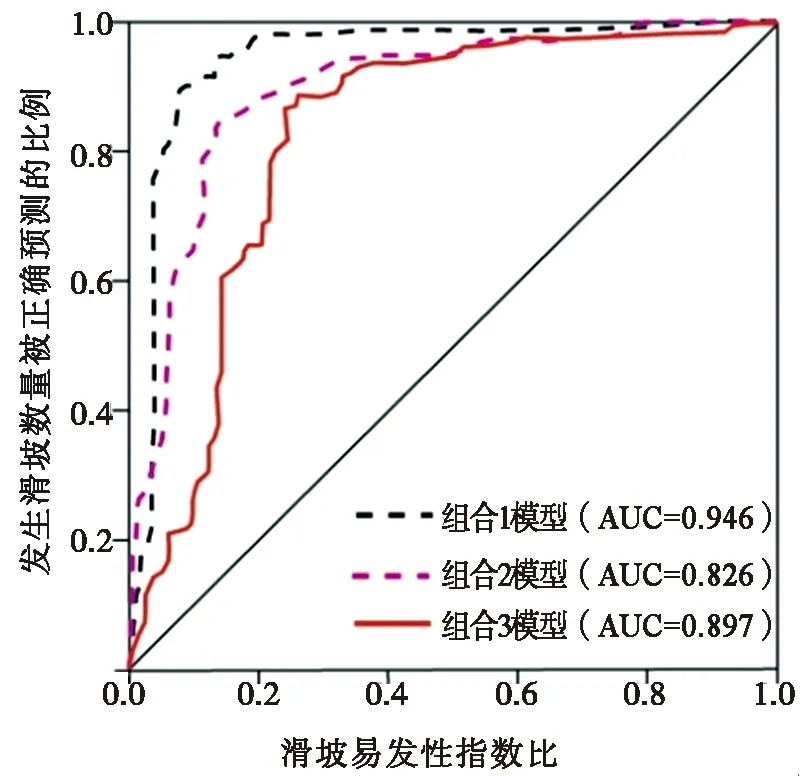
圖12 3種組合模型滑坡易發性評價預測率ROC曲線Fig.12 The prediction rate ROC curves of landslide susceptibility assessment for the three models

3種評價結果檢驗顯示，組合1模型預測精度和準確性要優于其它兩組模型，主要是因為信息量模型能較好地處理多因子組合帶來的復雜性和解決海量數據的差異性，再者研究區滑坡災害點信息資料詳細，能很好的適用自變量即可是連續的亦可是離散的邏輯回歸模型，二者組合的模型評價結果與實際吻合度較高。

5 結論

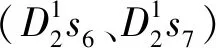
(2)在評價指標狀態分級劃分過程中，根據各指標條件下的I值、CF值和Wf值曲線突變點，同時結合滑坡面積及分級面積頻率曲線作為等級劃分的臨界值來確定因子分級狀態。該方法同時適用于連續型和離散型兩類指標，其本質是將對滑坡易發性相近區間進行組合，即充分考慮各因子狀態對滑坡的差異性影響，又避免了對狀態分級的主觀性劃分，體現了指標狀態分級的多樣性和合理性。

(3)通過對比3種模型的不同易發區內滑坡頻率比，利用Sridevi Jadi經驗概率法、Cohen′s Kappa系數法和ROC成功預測概率曲線法比較發現，組合1模型預測精度和準確性要優于其它兩組模型，說明采用信息量和邏輯回歸組合模型能夠較為客觀準確地對白龍江流域滑坡災害易發性進行評價。

(4)研究區滑坡極高易發區主要分布白龍江兩岸，尤其分布在兩河口至桔柑鄉段白龍江左岸區域。滑坡易發性受坪定～化馬斷裂控制作用明顯，沿斷裂帶發育強烈；極高易發區多集中軟弱千枚巖、炭質板巖組成志留系1段地層及由灰巖、千枚巖互層構成泥盆系6、7段，上覆殘坡積層的易滑地層區。易發性評價結果可為地質災害防治、國土空間規劃及用途管制提供有效支撐。