遺傳算法優(yōu)化神經(jīng)網(wǎng)絡(luò)的高校貧困生精準(zhǔn)認定
肖琪
(常熟理工學(xué)院,常熟215500)
0 引言
習(xí)近平總書記明確提出,堅決打贏脫貧攻堅戰(zhàn),確保2020 年我國現(xiàn)行標(biāo)準(zhǔn)下農(nóng)村貧困人口實現(xiàn)脫貧,脫貧縣全部摘帽[1]。在脫貧攻堅戰(zhàn)分層次分類的具體實踐中,其中包括根據(jù)貧困地區(qū)的人力結(jié)構(gòu)進行不同方式的教育扶貧[2]。教育扶貧領(lǐng)域,高等教育的精準(zhǔn)扶貧工作至關(guān)重要[3],一直是教育界甚至全社會廣泛關(guān)注的問題。為了做好高等教育領(lǐng)域的精準(zhǔn)扶貧[4]工作,很多高校都采取了建檔立卡的方式實現(xiàn)精準(zhǔn)資助[5],但由于地方工作粗放,存在建檔立卡貧困生識別不清的風(fēng)險。
目前各高校主要根據(jù)教育部文件的相關(guān)要求對貧困生進行主觀認定,這種認定方法存在很多主觀因素,影響了評定結(jié)果的準(zhǔn)確性。近年來,我國學(xué)者基于貧困生數(shù)據(jù)建立相關(guān)數(shù)學(xué)模型如決策樹法[6]、模糊綜合評價法[7]、層次分析法[8]、回歸分析法[3]等,但以上方法各有利弊,如回歸分析法針對線性關(guān)系的表達比較有效,而不能準(zhǔn)確反映非線性關(guān)系。柴政等人[9]采用反向傳播算法的前饋神經(jīng)網(wǎng)絡(luò)模型對高校貧困生等級進行評定,但容易陷入局部極小值。陸桂明等人[10]采用機器學(xué)習(xí)算法建立了XG-Boost 模型實現(xiàn)對高校貧困生等級的精確分類,但存在查準(zhǔn)率較低的問題。
BP(Back Propagation)神經(jīng)網(wǎng)絡(luò)模型是一種非常重要而經(jīng)典的人工神經(jīng)網(wǎng)絡(luò),具有高度非線性、自學(xué)性和映射性等優(yōu)點[12],它不需要尋求非線性樣本數(shù)據(jù)間的顯性關(guān)系式和數(shù)學(xué)模型,便可以準(zhǔn)確地逼近刻畫訓(xùn)練樣本數(shù)據(jù)規(guī)律的最佳函數(shù),從而克服現(xiàn)有客觀認定方法的許多局限性和困難。在實際應(yīng)用中,BP 神經(jīng)網(wǎng)絡(luò)存在收斂速度慢以及局部極小值等問題。為此,本文采用自適應(yīng)遺傳算法(Adaptive Genetic Algorithm,AGA)優(yōu)化BP 神經(jīng)網(wǎng)絡(luò)模型對高校貧困生等級進行精準(zhǔn)認定。
1 認定指標(biāo)體系的構(gòu)建
1.1 認定指標(biāo)的確定
本文利用常熟理工學(xué)院的學(xué)生樣本收集貧困生認定數(shù)據(jù)。從資助管理系統(tǒng)中導(dǎo)出該校貧困生信息,從中隨機抽取2015 名貧困生個體作為樣本。根據(jù)任俊等人[10]采用多粒度粗糙集理論挖掘影響貧困生精準(zhǔn)認定的關(guān)鍵性因素,從中篩選家庭人口數(shù)、父母親職業(yè)、家庭收入、家庭住房情況等10 個認定指標(biāo)作為輸入變量,貧困生等級作為輸出變量,具體如表1 所示。
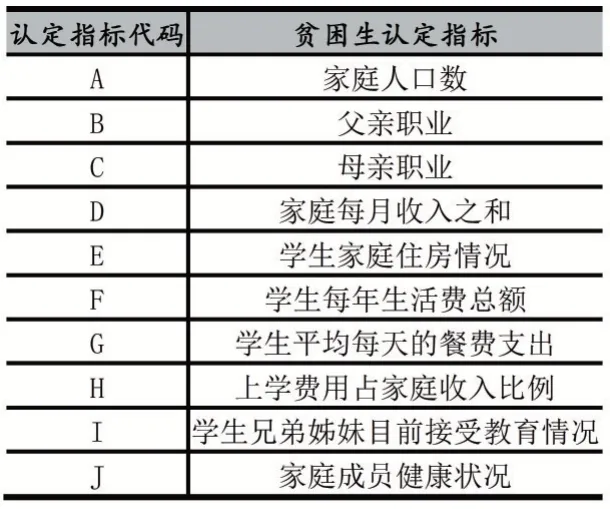
表1 貧困生認定指標(biāo)體系
1.2 樣本數(shù)據(jù)的量化
在對模型訓(xùn)練之前,需要對10 個認定指標(biāo)進行量化處理。各指標(biāo)的具體量化標(biāo)準(zhǔn)如表2 所示。如指標(biāo)A 是指家庭人口數(shù),賦值為1-4。當(dāng)家庭人口數(shù)6 人及以上時,A 為1;當(dāng)家庭人口數(shù)為5 人時,A 為2;當(dāng)家庭人口數(shù)為4 人時,A 為3;當(dāng)家庭人口數(shù)為3 人時,A為4。其他指標(biāo)按照此方法進行量化。模型的輸出變量是貧困等級,取值為1-3。當(dāng)學(xué)生特別貧困時,貧困等級為1;當(dāng)學(xué)生比較貧困時,貧困等級為2;當(dāng)學(xué)生一般貧困時,貧困等級為3。
根據(jù)上述數(shù)據(jù)處理方法,得到認定指標(biāo)量化數(shù)據(jù)如表3 所示。
在進行BP 神經(jīng)網(wǎng)絡(luò)預(yù)測之前,為避免原始數(shù)據(jù)過大造成網(wǎng)絡(luò)麻痹,要對原始數(shù)據(jù)進行歸一化處理。因此本文對表3 中的原始數(shù)據(jù)規(guī)范在[-1,1]之間,這樣可以盡可能地平滑數(shù)據(jù),從而消除預(yù)測結(jié)果的噪聲,歸一化的數(shù)據(jù)作為模型的訓(xùn)練樣本。
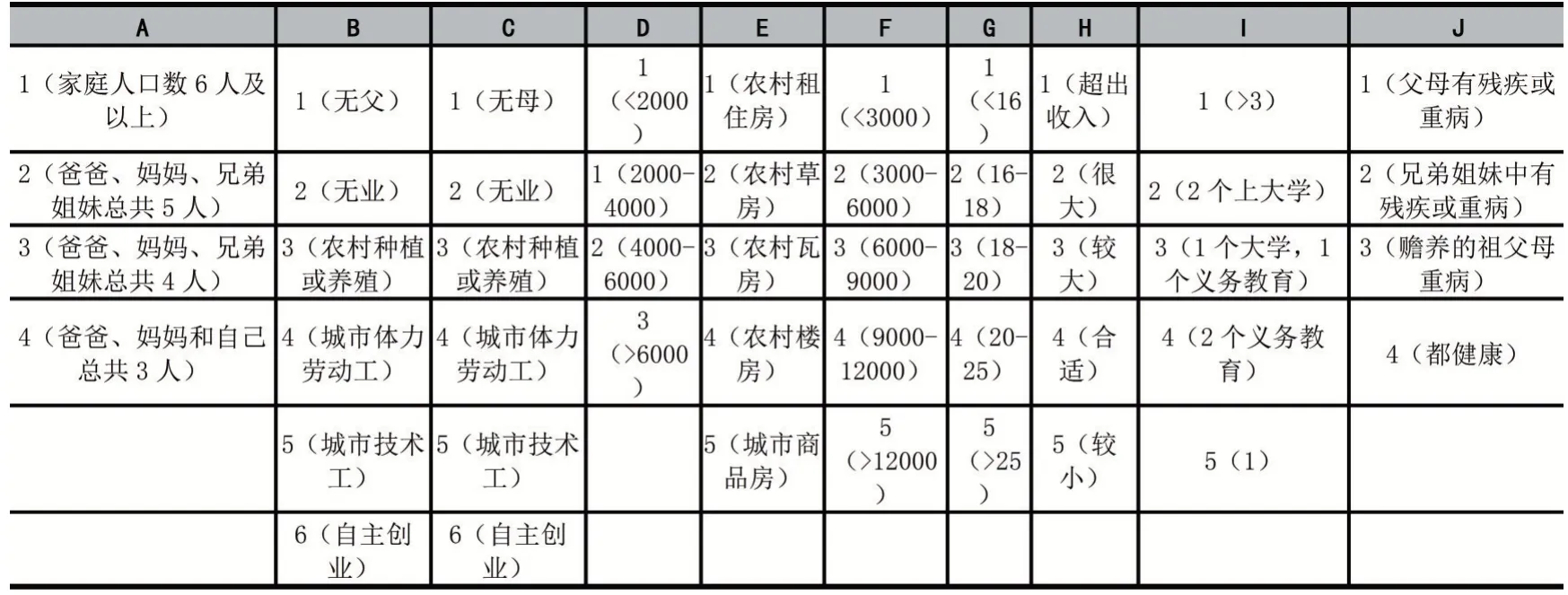
表2 貧困生認定指標(biāo)量化標(biāo)準(zhǔn)

表3 認定指標(biāo)量化數(shù)據(jù)
2 自適應(yīng)遺傳算法優(yōu)化模型
遺傳算法(Genetic Algorithm,GA)是一種模擬自然界遺傳機制和生物進化論而成的一種并行隨機搜索最優(yōu)化方法。遺傳算法優(yōu)化BP 神經(jīng)網(wǎng)絡(luò)簡稱(GA-BP)是用遺傳算法來優(yōu)化BP 神經(jīng)網(wǎng)絡(luò)的初始權(quán)值和閾值,使優(yōu)化后的BP 神經(jīng)網(wǎng)絡(luò)能夠更好地預(yù)測函數(shù)輸出。交叉概率和變異概率是影響遺傳算法性能的關(guān)鍵因素,因此,本文采用自適應(yīng)遺傳算法,通過自適應(yīng)交叉概率和變異概率來提高遺傳算法的性能。
GA-BP 模型是一種對網(wǎng)絡(luò)的權(quán)重和閾值進行全局搜索的過程。具體的流程如圖1 所示。

圖1 GA-BP模型流程圖
2.1 種群初始化
個體編碼方法為實數(shù)編碼,每個個體均為一個實數(shù)串,由輸入層與隱含層連接權(quán)值、隱含層閾值、隱含層與輸出層連接權(quán)值以及輸出層閾值4 部分組成。個體包含了神經(jīng)網(wǎng)絡(luò)全部權(quán)值和閾值,在網(wǎng)絡(luò)結(jié)構(gòu)已知的情況下,就可以構(gòu)成一個結(jié)構(gòu)、權(quán)值、閾值確定的神經(jīng)網(wǎng)絡(luò)。
2.2 適應(yīng)度函數(shù)
根據(jù)個體得到BP 神經(jīng)網(wǎng)絡(luò)的初始權(quán)值和閾值,用訓(xùn)練數(shù)據(jù)訓(xùn)練BP 神經(jīng)網(wǎng)絡(luò)后預(yù)測系統(tǒng)輸出,把預(yù)測輸出和期望輸出之間的誤差平方和的倒數(shù)作為個體適應(yīng)度值f,計算公式如式(1)所示。


式中,n 為網(wǎng)絡(luò)輸出節(jié)點,yi為BP 神經(jīng)網(wǎng)絡(luò)第i 個節(jié)點的期望輸出,oi為第i 個節(jié)點的預(yù)測輸出,E 為誤差平方和,f 為個體適應(yīng)度值。
2.3 遺傳操作
2.3.1 選擇操作
遺傳算法選擇操作有輪盤賭法、錦標(biāo)賽法等多種方法,本文采用輪盤賭法,即基于適應(yīng)度比例的選擇策略,每個個體i 的選擇概率pi為式(3)所示。

式中,fi為個體i 的適應(yīng)度值,pi為個體i 的選擇概率。
2.3.2 交叉操作
由于個體采用實數(shù)編碼,所以交叉操作方法采用實數(shù)交叉法,第k 個染色體ak和第l 個染色體al在j 位的交叉操作方法如式(4)所示。

式中,fmax為群體中最大的適應(yīng)度值,favg為群體的平均適應(yīng)度值,f’為要交叉的兩個個體中較大的適應(yīng)度值。k1,k2為常量系數(shù),分別取(0,1)區(qū)間的值。
2.3.3 變異操作
選取第i 個個體的第j 個基因aij進行變異,變異操作方法如式(6-7)所示:
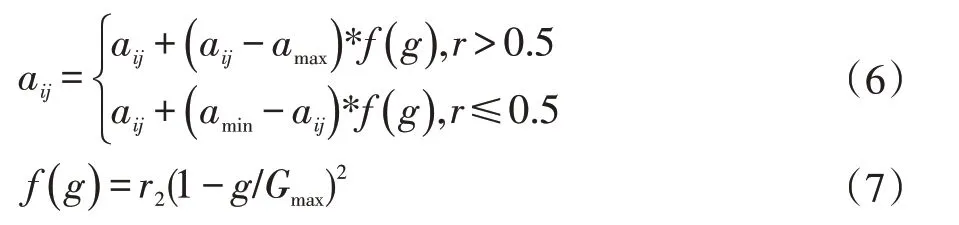
式中,amax為基因aij的上界;amin為基因aij的下界;r2為一個隨機數(shù);g 為當(dāng)前迭代次數(shù);Gmax為最大進化次數(shù);r 為[0,1]間的隨機數(shù)。
自適應(yīng)變異概率根據(jù)式(8)進行計算。
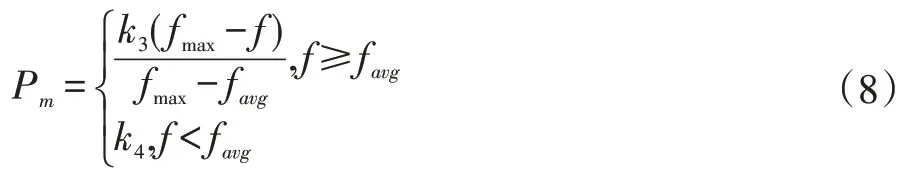
式中,fmax為群體中最大的適應(yīng)度值,favg為群體的平均適應(yīng)度值,f 為要交叉的兩個個體中較大的適應(yīng)度值。k3,k4為常量系數(shù),分別取(0,1)區(qū)間的值。
3 模型的評價方法
本文對模型準(zhǔn)確性的評價方法是根據(jù)預(yù)測等級與真實貧困等級之間的誤差來判定的。誤差的評估采用相對誤差百分比、均方根誤差和平均絕對誤差作為評估指標(biāo),具體計算如式(9-11)所示。
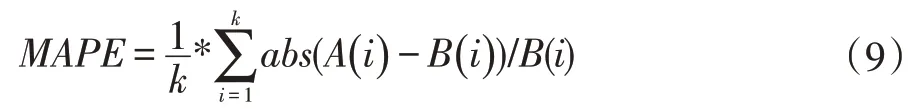
式中,MAPE 為相對誤差百分比,abs 為絕對值,A(i)為模型輸出值,B(i)為實際值,k 為樣本數(shù)量。
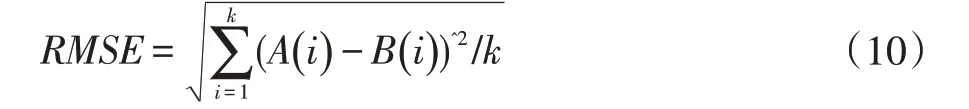
式中,RMSE 為均方根誤差,k 為表示樣本數(shù)量,A(i)為示模型輸出值,B(i)為實際值。
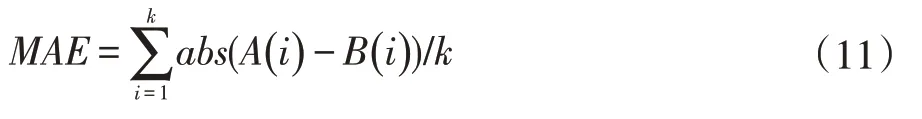
式中,MAE 為示平均絕對誤差,abs 為絕對值,A(i)為模型輸出值,B(i)為實際值,k 為樣本數(shù)量。
4 模型的構(gòu)建
4.1 隱含層節(jié)點數(shù)的確定
模型對高校貧困生等級進行預(yù)測,分為訓(xùn)練和驗證兩個部分。從表3 中選取1800 組數(shù)據(jù)作為訓(xùn)練樣本,100 組數(shù)據(jù)作為測試樣本,15 組數(shù)據(jù)作為驗證樣本。因此,訓(xùn)練樣本的輸入節(jié)點數(shù)為10,輸出層節(jié)點數(shù)均為1,隱含層節(jié)點數(shù)根據(jù)公式(12)計算。

式中,N 為隱含層節(jié)點數(shù),m 為輸入節(jié)點數(shù),n 為示輸出節(jié)點數(shù),a 為[1,10]之間的常數(shù)。根據(jù)式(12),本文隱含層節(jié)點取值范圍為[4,13]。根據(jù)隱含層節(jié)點的取值范圍,改變數(shù)值,
本文利用MATLAB R2016 自帶的人工神經(jīng)網(wǎng)絡(luò)工具箱來完成模型的建立。根據(jù)隱含層節(jié)點數(shù)的取值范圍對貧困生數(shù)據(jù)進行訓(xùn)練,不同隱含層節(jié)點數(shù)的BP 模型預(yù)測誤差如表4 所示。從表4 可以看出,誤差最小時對應(yīng)的隱含層節(jié)點數(shù)為6。這主要是因為隱含層節(jié)點數(shù)過少時,不足以反映訓(xùn)練數(shù)據(jù)的客觀規(guī)律,誤差會出現(xiàn)波動;隱含層節(jié)點數(shù)數(shù)過多時,會增加網(wǎng)絡(luò)學(xué)習(xí)時間,可能出現(xiàn)“過擬合現(xiàn)象”,也會導(dǎo)致誤差較大。因此,隱含層節(jié)點數(shù)的選取要適中。
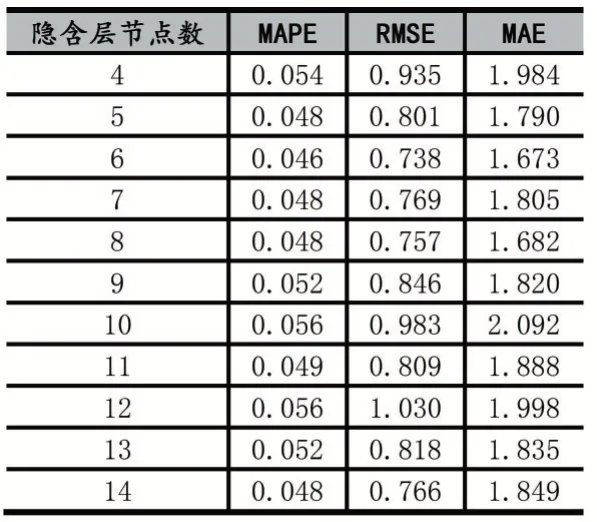
表4 不同隱含層節(jié)點數(shù)BP 模型的預(yù)測誤差
4.2 輸入層和輸出層的傳遞函數(shù)確定
輸入層和輸出層的傳遞函數(shù)選取宗旨是使預(yù)測準(zhǔn)確。在網(wǎng)絡(luò)結(jié)構(gòu)和權(quán)值、閾值相同的情況下,BP 模型預(yù)測誤差與隱含層、輸出層的傳遞函數(shù)之間的關(guān)系如表5 所示。
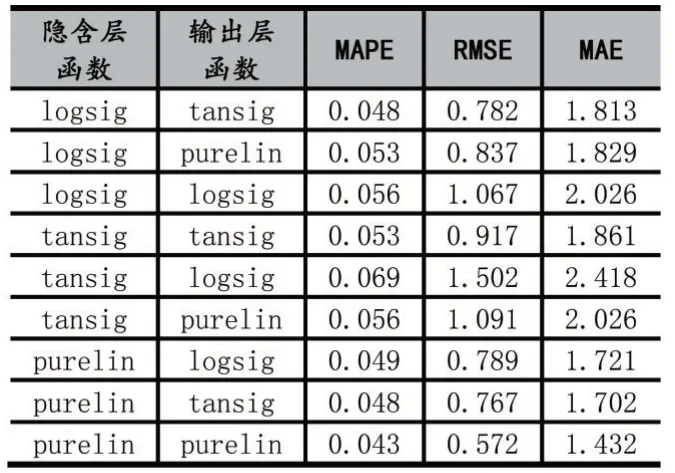
表5 不同傳遞函數(shù)對應(yīng)的預(yù)測誤差
從表5 可以看出,隱含層和輸出層的傳遞函數(shù)選擇對BP 模型預(yù)測精度有較大影響。其中誤差最小的隱含層和輸出層的傳遞函數(shù)分別為purelin、purelin。
4.3 訓(xùn)練參數(shù)的確定
根據(jù)上述模型參數(shù)的確定,相關(guān)訓(xùn)練參數(shù)的設(shè)置如表6 所示。
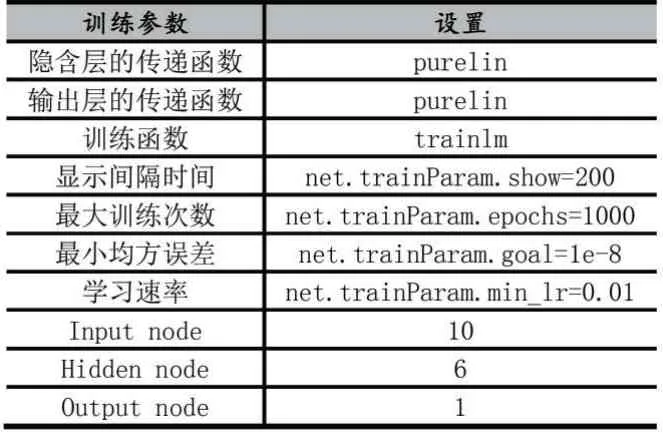
表6 訓(xùn)練參數(shù)的設(shè)置
根據(jù)上述訓(xùn)練參數(shù),訓(xùn)練BP 神經(jīng)網(wǎng)絡(luò)。高校貧困生的貧困等級預(yù)測值與實際值對比結(jié)果如圖2 所示。從圖2 可以看出,BP 模型對貧困生等級的預(yù)測結(jié)果與實際貧困等級之間偏差比較大。實際值和預(yù)測值之間的接近程度一般采用相關(guān)系數(shù)來表征。對BP 模型的預(yù)測結(jié)果進行相關(guān)性分析,結(jié)果如圖3 所示。從圖3可以看出,BP 模型對貧困生的貧困等級預(yù)測的相關(guān)系數(shù)為0.23。
5 結(jié)果與討論
采用GA-BP 模型、AGA-BP 模型分別對網(wǎng)絡(luò)進行訓(xùn)練和測試。GA-BP 模型的測試結(jié)果如圖4 所示。從圖4 可以看出,GA-BP 模型對貧困生等級的預(yù)測值與實際值的接近程度比BP 模型有所改善。這主要是因為GA-BP 模型克服了局部最小值的缺陷。對貧困生等級的相關(guān)度分析如圖5 所示。從圖5 可以看出,GA-BP 模型對貧困生等級預(yù)測的相關(guān)系數(shù)為0.80。與BP 模型的相關(guān)系數(shù)對比,GA-BP 模型在預(yù)測相關(guān)性上有所改善。
AGA-BP 模型的測試結(jié)果如圖6 所示。從圖6 可以看出,AGA-BP 模型對貧困生等級的預(yù)測值與實際值比較一致。這主要是因為AGA-BP 模型相比GABP 模型來說,通過不斷調(diào)整交叉概率和變異概率,更能夠平衡局部搜索和全局搜索能力,有效避免了GABP 模型出現(xiàn)早熟收斂問題,從而找到內(nèi)部最優(yōu)解。AGA-BP 模型貧困生等級的相關(guān)度分析如圖7 所示。從圖7 可以看出,AGA-BP 對貧困生等級預(yù)測的相關(guān)系數(shù)為0.96。與GA-BP 的相關(guān)系數(shù)對比,優(yōu)化模型在預(yù)測相關(guān)性上有了很大改善。
為了驗證遺傳算法優(yōu)化模型的優(yōu)越性,利用15 組驗證樣本數(shù)據(jù)對三個模型的預(yù)測精度進行驗證,結(jié)果如表7 所示。從表7 可以看出,AGA-BP 模型的預(yù)測誤差最小,即預(yù)測精度最高。因此,AGA-BP 模型的預(yù)測效果比BP 模型、GA-BP 模型的預(yù)測效果更好。
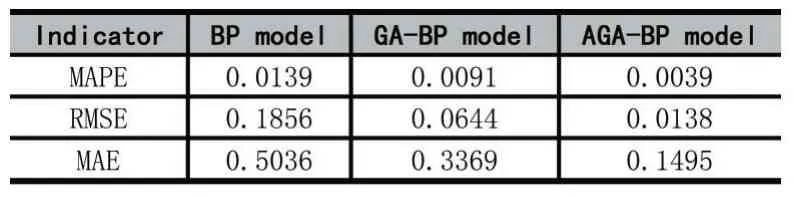
表7 各模型的預(yù)測誤差對比
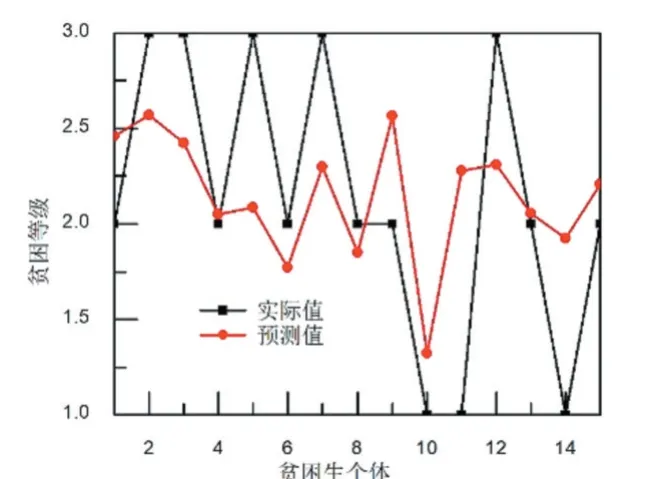
圖2 BP模型的預(yù)測結(jié)果
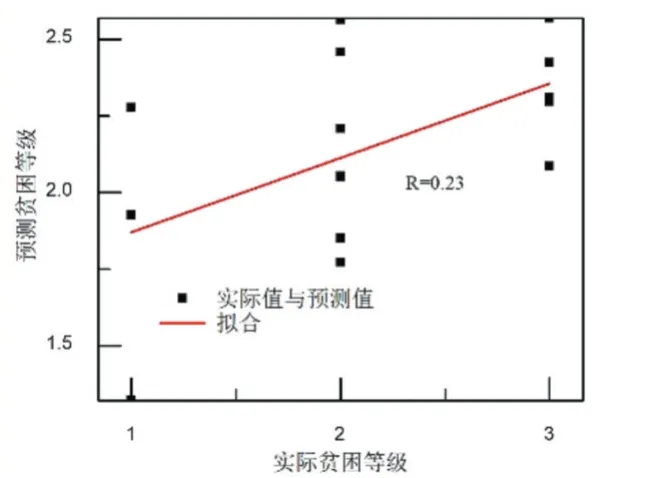
圖3 BP模型的相關(guān)性分析
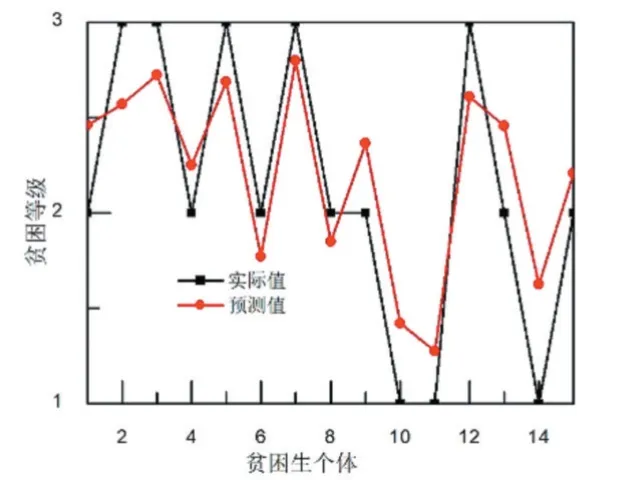
圖4 GA-BP 模型的預(yù)測結(jié)果
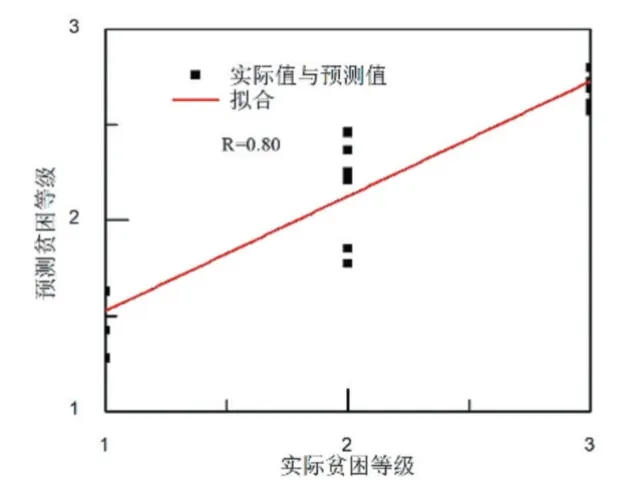
圖5 GA-BP 模型的相關(guān)性分析
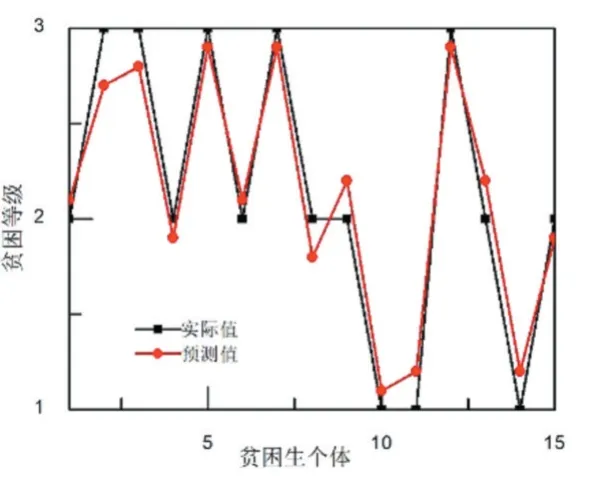
圖6 AGA-BP 模型的預(yù)測結(jié)果
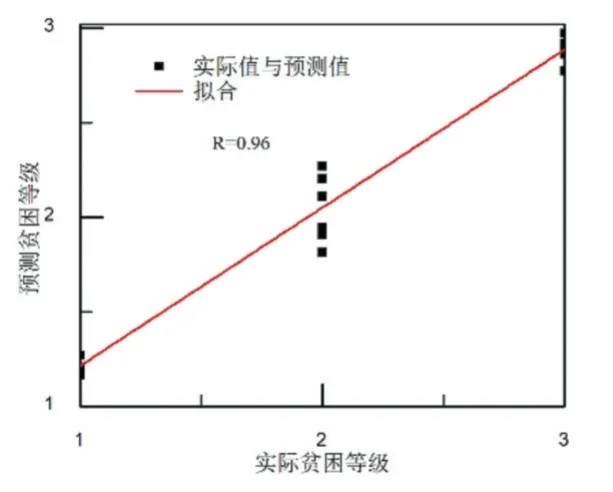
圖7 AGA-BP 模型的相關(guān)性分析
6 結(jié)語
自適應(yīng)遺傳算法優(yōu)化的BP 神經(jīng)網(wǎng)絡(luò)模型能有效表明具有非線性關(guān)系的輸入量與輸出量之間的關(guān)聯(lián)性。由于高校貧困生等級與其主要認定指標(biāo)間存在著復(fù)雜的非線性關(guān)系,篩選家庭成員數(shù)、父親職業(yè)、母親職業(yè)等10 個認定指標(biāo)作為神經(jīng)網(wǎng)絡(luò)模型的輸入?yún)?shù),對高校貧困生等級進行預(yù)測,對比了BP 模型、GA-BP模型、AGA-BP 模型的相關(guān)系數(shù)、預(yù)測精度。結(jié)果表明,采用自適應(yīng)遺傳算法優(yōu)化的BP 神經(jīng)網(wǎng)絡(luò)模型預(yù)測貧困生等級更接近真實情況,充分說明自適應(yīng)遺傳算法優(yōu)化神經(jīng)網(wǎng)絡(luò)對高校貧困生精準(zhǔn)認定的有效性。

