基于模糊系統的飛行沖突探測與解脫

馮思嘉，季玉龍

（1.四川大學視覺合成圖形圖像技術國防重點學科實驗室，成都610065；2.四川大學空天科學與工程學院，成都610065）

0 引言

隨著民航企業的發展，飛行流量的增加，有限的空域資源逐漸不能滿足增加的交通流量，導致兩者之間的矛盾變得日益突出，因此對飛行安全、效率、空管服務品質有了更高的要求[1]。這樣的問題在進近區域體現更加顯著[2]。智能化的沖突管理能夠對潛在沖突進行探測，若發現有沖突則對飛機航向進行微調，能有效的使飛機匯聚在一起時并保持一定的安全間隔，這樣智能化的沖突管理能為管制員提供輔助決策，減輕他們負擔的同時提高進近空域資源的利用率，為完善航空管理體制與運行機制做貢獻。

飛機智能化沖突管理核心主要包括兩部分：沖突探測與沖突解脫[3]。沖突探測是對飛機的軌跡進行預測，然后判斷航空器是否小于間隔標準，如果有小于則判定為存在潛在沖突，發出沖突警告。對于存在潛在沖突的飛機進行沖突解脫，即為它盡快重新規劃一條以飛機耗能少為原則的無沖突路徑。飛機在空中情況是瞬息萬變的，很多因素都會影響到路徑規劃，同時又伴隨著許多不確定性和隨機性，使得系統輸入參數過多，過于復雜。

模糊控制能夠有效解決上述難題，模糊控制具有穩定性高、適應性強，計算效率高等優點，能高效處理輸入較多的情況[4]。傳統的模糊系統使用專家知識將模糊邏輯用于智能控制，Hagras 提出了FLS[5]，這種模糊邏輯可以提高在不確定條件下模糊系統的性能，以便在動態變換的環境中實現智能控制。Mobadersanyetal[6]，提出了一種基于模糊邏輯的實時方法來解決由未知移動障礙引起的路徑規劃問題。FLS 具有固有魯棒性，非常適用于現實生活中的應用。FLS 也已經針對PID控制器進行了調整[7-8]，而調整之后PID 不再使用恒定比例積分和微分，這些值會根據當前誤差不斷更新。然而隨著輸入輸出的增加，手動調整FLS 的隸屬函數和規則庫的參數變得越來越困難。Jang 提出了一種ANFSIS[9]體系結構，該過程用反向傳播算法對模糊系統的隸屬函數和規則庫進行調整。Shimojima[10]提出了一種基于GA 的監督學習機制。Jain[11]提出了一種使用模擬退火的優化過程。人工神經網絡（ANN）也被用于開發控制器。通過強化學習對控制對象進行訓練，以便在每個瞬間采用最佳行動以達到最終的期望狀態。Q-learning 作為強化學習的一種，在神經網絡中應用廣泛，其中包括了Atari 游戲[12]，以及AlphaGo[13]系統等。Sathyan 等人分別使用強化學習和模糊系統對機器人進行訓練，對比之下發現由于模糊系統的固有魯棒性以及擅長對非線性系統的處理，使得模糊系統訓練出的機器人任務成功率更高。

因此本文使用模糊系統來解決飛機沖突問題，將每一個飛機建立稱為模糊子系統，利用當前飛機的相對位置判斷飛機是否在其他飛機的保護半徑之內，如果在，則獲取當前兩架飛機的相對接近速度和航向，通過這兩個參數判定是否存在潛在沖突，如果不存在則不對其進行改變，讓飛機保持原有的航向和速度進行飛行，如果存在則將相對位置、相對速度、相對航向作為模糊系統的輸入，輸出飛機的新航向，對飛機的軌跡進行修正，使得飛機在保證分離的情況下飛行路徑最短，節省能耗。

本文第二部分對沖突探測和沖突解脫的邏輯模型進行解釋說明，第三部分是對該系統的具體描述，第四部分是實驗的建立與實驗結果說明，最后第五部分是總結。

1 碰撞情景與系統框架建立

本文中，我們需要為進近范圍內存在潛在沖突的飛機規劃出一條無沖突路徑，測試范圍是一個以100km 為半徑的圓形區域。如果被判定為存在潛在沖突，則需要依據優先級對飛機路徑進行重新規劃，重新規劃的原則是：

（1）被改變的飛機數目盡量少；

（2）遵循設定好的優先級；

除上述的原則以外，結合飛機實際的飛行情況，進行實驗的飛機速度介于150m/s～220m/s 之間，模糊系統對飛機航向的改變角度不超過30°。

圓形內部即為進近區域，飛機在進近范圍外時，沖突保護距離為5nmi，當進入進近范圍內之后，考慮到飛機數目雖然增加，因此沖突保護距離縮小為2.5nmi。進入進近范圍的飛機，其所有基礎航向都是朝向機場降落位置，每隔0.3 秒進行一次更新，并且計算出兩兩之間的相對距離，判定是否在對方的保護半徑之內，如果在則獲取兩架飛機的相對航向，如果兩架飛機是相向而行則使用模糊系統對優先級較低飛機的航向進行改變。以2 架飛機為例，其沖突模型的建立如圖1 所示。A 與B 為兩架進入測試范圍的飛機，其航向分別為HA 與HB。

圖1 沖突模型建立

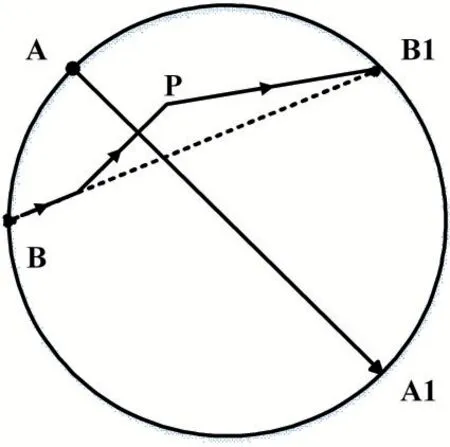
圖2 更改航向模型

如果不對飛機航向進行修正，飛機則會發生沖突，通過將每個飛機都建模成一個模糊子系統來解決此次沖突問題，每個模糊子系統對應著3 個輸入和1 個輸出，輸入分別是相對航向、相對速度以及相對距離，輸出是轉彎率。圖3 所示即為期望的被更改航向之后的模型圖。

2 沖突探測與解脫

2.1 沖突探測

沖突探測是判定飛機之間的間隔是否小于間隔標準，傳統的方法是判定到小于最小間隔標準之后則發出沖突預警[14]，并未對小于標準間隔的飛機對進行相對航向的判定，假設兩架飛機雖小于安全間隔，但是航向相反，則不會發生沖突，這里將其稱為假性沖突，如果對存在這種沖突的飛機對進行路徑的重新規劃，則會對資源進行浪費，因此論文除了會對沖突間隔進行建模，還會對相對航向進行判定。

（1）沖突間隔與保護區建立

最小安全間隔會隨著軌跡的密度和空域區域而改變，一般而言，在一段航路空域中，兩架飛機的水平最小安全間隔的公認值為5nmi，而在飛機降落和進場的進近扇區中該值會減少為2.5nmi。

飛機的保護模型主要分為以下三種：長方體保護模型、橢球形保護模型、圓柱體保護模型。由于保護區域的連接函數需要分開進行表示，且各個表面連接處不可導，導致后續計算較為復雜。因此為方便計算設計了橢球體模型和圓柱形模型。在論文中采用圓柱體模型如圖3 所示。

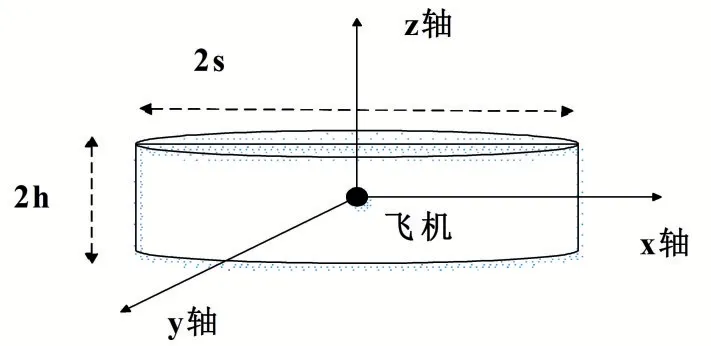
圖3 保護模型建立

以飛機為模型質點中心，高為2 倍危險接近的最大高度0.2nmi，以最小保護半徑為半徑s 建立圓柱體。任何進入建立保護區域的其他飛機被定義為小于沖突半徑。飛機的圓柱體保護模型所建立的區域范圍可以表示為：

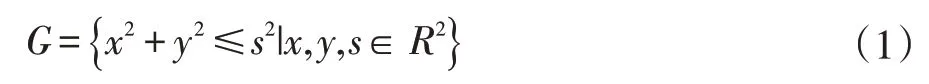
（2）相對位置與航向判定

在本文中需要對處于保護區內的存在潛在沖突的飛機進行航向的判斷。假設已經檢測到飛機A 在飛機B 的保護區域之內。

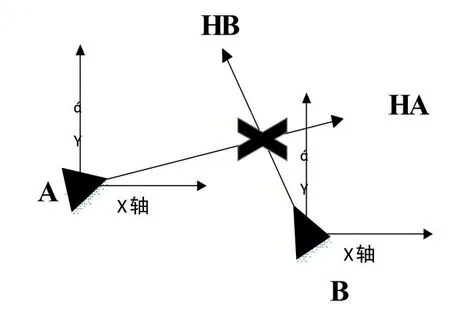
圖4 相對位置判定示意圖

獲取到當前時刻飛機A 的航向為HA，飛機B 的航向為HB，相對航向：

由于直接比較HAB會有許多種情況且有不確定性，而在飛機的控制中最重要的就是實時性，如果為了追求過度的精準而拾取算法的實時性是不合理的，因此為了避免對相對航向進行分類討論而增加復雜性，所以在一開始對飛機的相對位置進行計算，這種計算是合理的因為如果飛機有發生相撞的可能性，在調用模糊系統時也是需要對相對位置進行計算的。

所以在計算相對航向之前先進行相對位置的判定，假設飛機A 的橫坐標為XA，飛機B 的橫坐標為XB，判斷的值XAB=XA-XB，如果XAB>0，則飛機A 在飛機B的相對右邊，反之則為左邊。考慮一種情況，當飛機A在飛機B 的相對左邊時，如果飛機A 的航向屬于[0,180]這個范圍，且飛機B 的航向屬于[180,360]這個范圍時，就算兩架飛機距離較近，也不會實際發生碰撞，但若不滿足上述條件，則有發生碰撞的可能性，即需要通過模糊系統對航向進行修正。

2.2 基于模糊樹的沖突解脫

本文采用模糊系統對具有潛在沖突的飛機進行航向調整。模糊控制是基于經驗和知識的一種規則控制，在控制中可以對復雜的數學模型進行控制，具有控制機制容易實現過程簡單的特點。相比于CNN 等深度學習算法[15]，模糊系統不需要其他輔助特征信息的輸入，在該模糊系統中輸入包含：相對航向、相對速度、接近率，對應的輸出為對飛機航向。在獲取輸入之后需要對輸入進行歸一化處理。優先級較低的飛機的航向改變之后，考慮到飛機本身的限制，在對航跡進行計算的時候，應使新產生的點在其轉彎半徑上。同時由于模糊系統過程簡單精度不高，這導致在飛機進入機場準備降落時，不能夠精準地到達預期位置，所以在進近范圍內時，采用模糊系統進行控制。

建立模糊系統有如下步驟：

①確定輸入和輸出變量，對輸入變量進行歸一化處理；

②確定輸入變量和輸出變量的隸屬度函數；

③使用if-then 語言，建立模糊規則；

④得到相應的輸出；

⑤去模糊化處理。

在本文中，模糊系統將兩架可能發生沖突的飛行器的相對距離、相對航向以及接近率作為輸入。即可能發生沖突的飛機A 與飛機B 對模糊系統的相對航向、相對距離、接近率可以分別用以下式子進行表示：

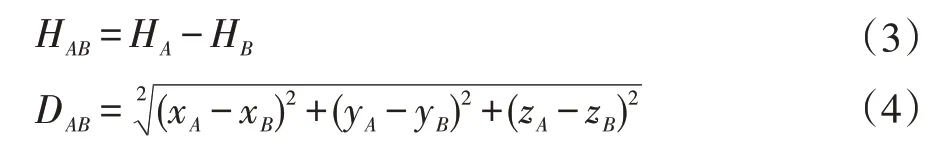
值得說明的是在這里計算的相對航向與上述的有所不同，這里用優先級更高的飛機作被減數，在這個例子中飛機A 擁有更高的優先級（飛機A 比飛機B 離降落點更近），其中DAB表示飛機A 與飛機B 之間的直線距離，VA和VB表示A 與B 兩架飛機的速度。

川系火鍋是我們最常見的火鍋類型，我想，提起火鍋一半人想到的是麻辣，另一半人想到的就是川渝。川系火鍋一般認為分為四川火鍋、重慶火鍋、魚頭火鍋以及串串香。

在對相對航向計算完后，判斷其結果的正負：

如果Heading＜0，則Heading=HA-HB+360；

如果Heading＞0，則Heading=HA-HB。

在進行了上述判定之后，進一步對入和輸出進行歸一化的處理（以Heading＞0 為例）用以下式子進行處理：

其中R 表示保護半徑（不同區域內飛機保護半徑不同），Vmax表示飛機最大飛行速度。本文將飛機航向偏轉度作為模糊系統的輸出，由于前面的輸入是進行過歸一化的處理，因此通過模糊系統的輸出也是一個歸一化的值。考慮到飛機性能的限制，不可能做出過大的轉彎幅度，所以經過模糊系統實際輸出的值乘最大偏轉度，才是實際的偏轉角度。飛機的最大偏轉角度用Tmax表示，模糊系統輸出的歸一化值用out 表示，因此實際的偏轉角度用Turn 表示為：

在構建隸屬度函數的時候采用三角隸屬函數對其進行構建。三角隸屬函數模糊化運算比較簡單，且模糊化結果具有一定的魯棒性。由于有三個輸入，因此對應有三個小的模糊子系統，分別對它們進行隸屬度函數建立。

對于相對航向而言，可以通過比較值的大小來判斷兩個飛機的相對位置，以飛機A 擁有更高優先級為例，如果歸一化之后的值小于0.5，則可以判定飛行器B 在飛行器A 的左側。如果是大于0.5 則飛行器B 在飛行器A 右側，因此可以構建如圖5 所示的隸屬函數。

同理對相對距離和相對接近率建立如圖6-圖7 所示的隸屬度函數。

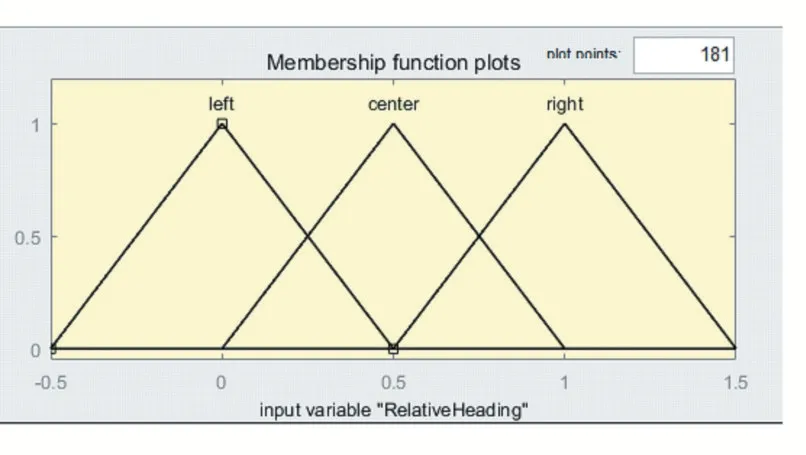
圖5 相對航向隸屬函數

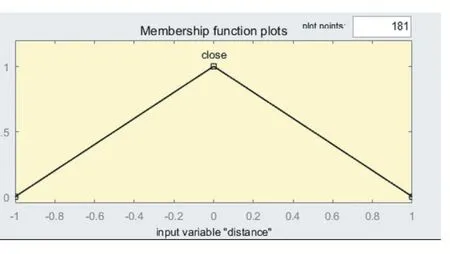
圖6 相對距離隸屬度函數

圖7 相對接近率隸屬度函數

在建立模糊規則之后，不同的三個輸入變量經過模糊規則進行處理之后得到一個介于0 和1 之間的輸出變量，然而這里的輸出變量不能直接作為輸出傳給飛行器，因此還要經過去模糊化這一過程。將模糊的輸出轉換為精確的系統能操作的量。在本文中采用重心法。

3 實驗建立與分析

3.1 總體構建

該程序運行的界面效在實驗區域內，隨機在不同位置生成10 架飛機，隨機給予它們一個合理的初始速度和初始航向，飛行開始后，這10 架飛機每隔0.3 秒計算一次兩兩之間的間隔，這里需要說明的是每架飛機其實相當于時一個模糊子系統，當判定到保護半徑內存在有危險的飛機時，使用模糊系統對存在沖突的飛機的飛行軌跡進行修改。例如在某次實驗中，檢測到飛機A 與飛機B 有沖突發生的可能性，且通過判定飛機A 的優先級高于B，則將飛機A 與B 的距離，A 與B的航向差，以及速度差，進行歸一化處理之后，作為飛機B 模糊子系統的三個輸入，通過設定的模糊規則，計算出飛B 的新航向。雖然可能出現，飛機B 改變航向飛行了一段時間后與飛機F 有了沖突，但是由于仿真系統每隔0.3 秒就進行一次距離計算，使得飛機有足夠距離在相撞之前調整開距離。

3.2 實驗驗證

該以某次實驗為例，隨機生成飛機之后，從系統中得知A 飛機與B 飛機有沖突的可能性，立即產生沖突預警如圖8 所示。

圖8 沖突預警圖

圖9 為兩飛機的飛行間隔距離隨著仿真之間變化而變化的圖，從圖中可以看出仿真開始時，兩飛機距離是13000m 左右，小于保護半徑，經過模糊系統的調整之后，飛機在仿真38 秒左右到達距離最近9000m，之后兩架飛機的距離則逐漸變大，直到80 秒左右，逐漸離開相互的保護半徑，沖突警告關閉。

同時我們觀察飛機B 的航向隨時間變化的曲線圖，如圖10 所示，飛機B 的航向一開始是150 度，因為和飛機A 有沖突后，且優先級低于飛機A，因此對航向進行調整，從此圖可看出，飛機的航向改變是緩慢的，不是一瞬間就完成的，在80 秒左右飛機航向保持不變，同時結合兩家飛機的距離圖，80 秒左右時，兩飛機逐漸離開相互的保護半徑。

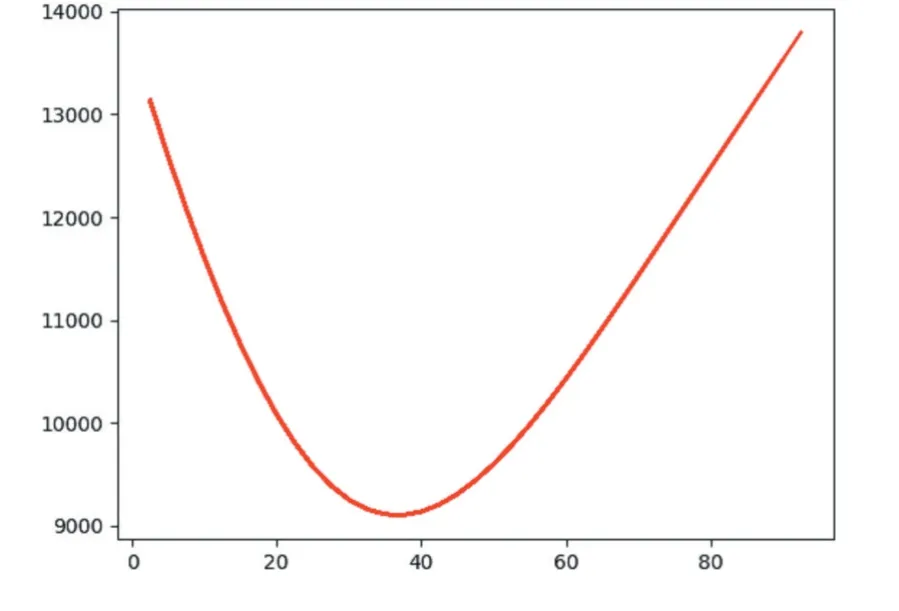
圖9 保護半徑變化曲線

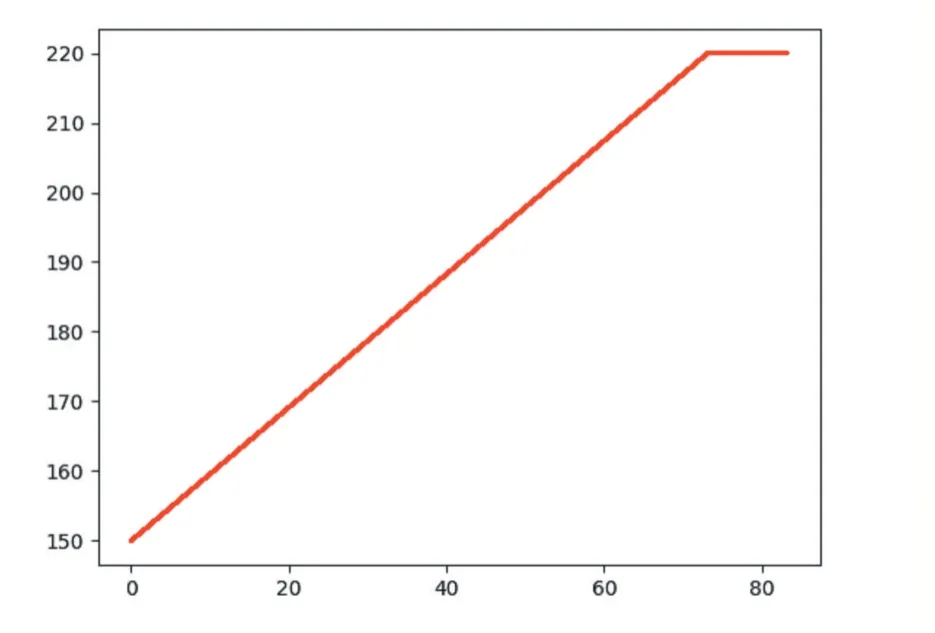
圖10 改變后保護半徑

總體上來看，一開始飛機A 與飛機B 相向而行，并且在相互的保護半徑范圍之內，從圖11 中可以看出，飛機B 改變了航向，從而避免了碰撞的產生。

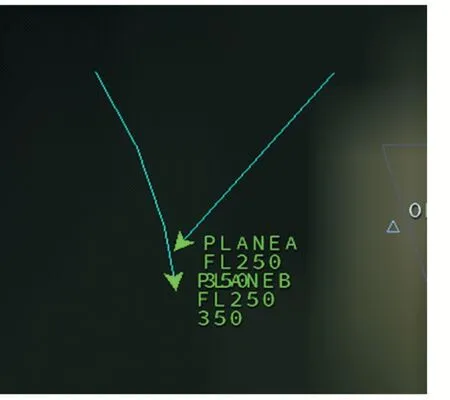
圖11 飛行軌跡圖

4 結語

在對飛機實行沖突管理時，由于存在許多外界不確定因素，使得系統的輸入量較大，模糊系統具有魯棒性、適應性強、高性能、計算效率高的特點，能有效解決上述難題，因此采用模糊控制對飛機飛行路徑進行規劃，通過上述實驗可以看出，原本有沖突可能的兩架飛機在通過模糊系統的運算之后，優先級較低的飛機通過改變航向的方式，避免了沖突的發生。