變電站軟導線端部力矩的計算

(中國電力工程顧問集團華東電力設計院有限公司，上海 200001)

0 引言

在變電站設計中，計算軟導線兩端的約束反力時，通常只考慮力而不考慮力矩，這是因為通常認為軟導線是絕對“柔軟”的，即認為軟導線只有抗拉剛度，沒有抗彎強度[1-3]。但實際情況并非如此，尤其是當軟導線直徑較大，或者采用多分裂導線時，軟導線的抗彎強度是不可忽略的。由于軟導線具有抗彎強度，因此導線端部就會存在約束力矩，該力矩作用在設備的端子板上，可能對端子板造成損壞。

本文考慮了軟導線的抗彎強度后，推導了軟導線的力學方程，給出了端部力矩的計算方法，并提供了幾個工程算例。

1 軟導線的力學模型

建立坐標系，令Y軸垂直于地面，X軸平行于地面，軟導線兩端點的坐標分別為(0，0)和(L，h)，兩端點與地面的夾角分別為θ1和θ2。假設導線只受重力作用，單位長度的導線所受重力為q。如圖1所示。

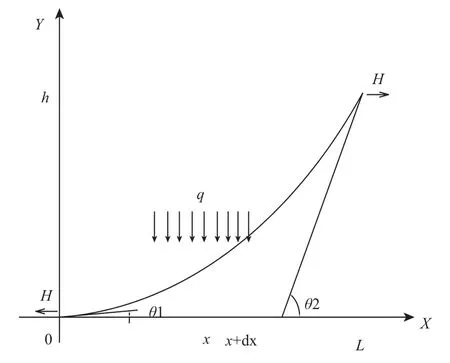
圖1 軟導線示意圖

取軟導線中的一個“dx”微段作分析，受力如圖2所示；由于考慮到導線的抗彎強度，微段的兩端不僅受力的作用，還有力矩作用。同理，導線所受的水平力和垂直力的合力方向不再沿導線的切線方向，這一點是與未考慮抗彎強度時有區(qū)別的。

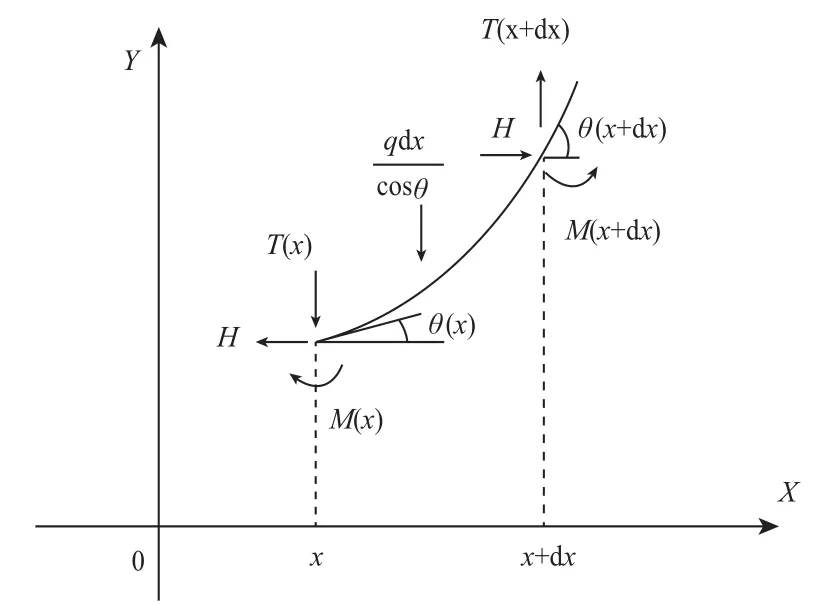
圖2 軟導線受力分析

根據(jù)受力和力矩平衡條件，有如下的關系式。

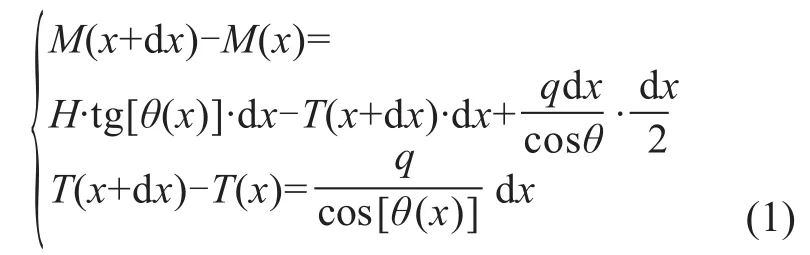
設軟導線的方程為y=f(x)，則(1)式中的

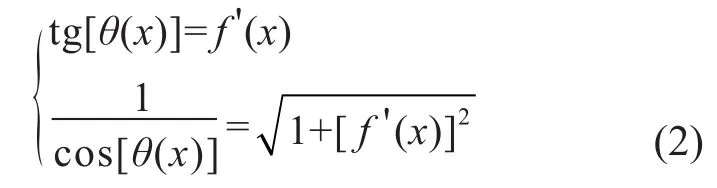
將(2)式代入(1)式，同時將(2)式右端的“dx”移到左端，并略去高階無窮小量，可得：

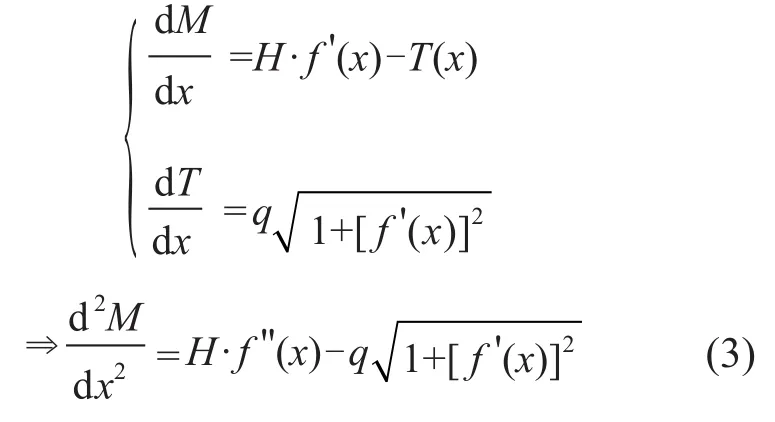
將導線看作一根桿件，根據(jù)材料力學[4]，桿件上的彎矩可表達為：

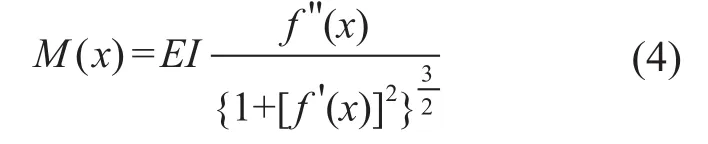
其中E為材料的彈性模量，I為桿件的截面系數(shù)。

將(4)式代入(3)式，得到：

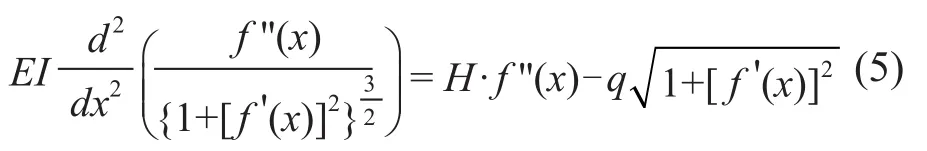
式(5)是考慮到抗彎強度后軟導線的力學方程。這是一個四階的非線性微分方程，而且方程中還有一個未知數(shù)“H”，即軟導線所受的水平力；要解這樣一個微分方程，需要5個已知條件。導線兩端的邊界條件共有4個，即兩端的函數(shù)值和一階導數(shù)值；導線的弧垂可以作為第5個已知條件。

若I=0，即忽略軟導線的抗彎強度，則式(5)退化為常見的軟導線方程；若H=0，即導線端部為水平滑動連接、水平方向上沒有約束，則式(5)退化為常見的支撐管母線方程。

2 軟導線方程的求解

式(5)是軟導線精確的微分方程，但由于是非線性的，求解困難，因此在工程應用時需要對其作一定的近似。方程中的非線性主要來源于項，當導線的弧垂與導線長度相比較小時，，將該近似表達式代入式(5)，并令則軟導線的方程可近似為一個線性微分方程[5-7]。

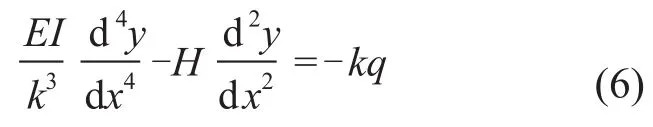
式(6)是一個四階的線性微分方程，其通解為：

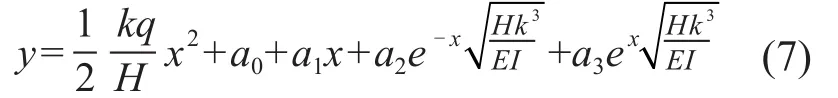
其中a1，a2，a3，a4為待定系數(shù)，由微分方程的邊界條件決定。軟導線微分方程的邊界條件如下。

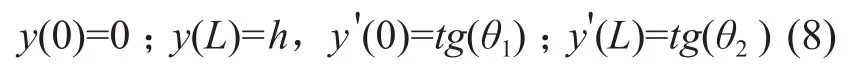
將邊界條件代入式(7)，可以求解出待定系數(shù)如下。

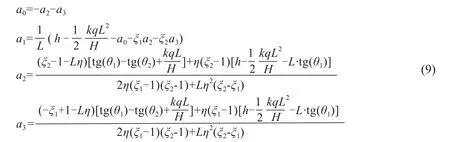
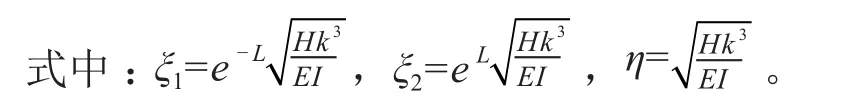
求解出四個待定系數(shù)后，仍存在一個未知數(shù)“H”，即導線的水平力未知。通常軟導線的弧垂是已知的，可通過弧垂反推出“H”，具體方法可采用試湊法，這里不贅述。

根據(jù)式(4)，軟導線任一點的力矩為：

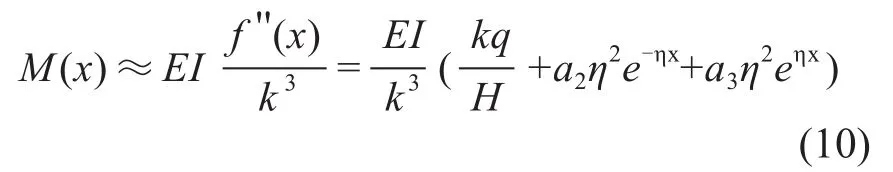
根據(jù)式(3)，導線任一點的垂直力為：

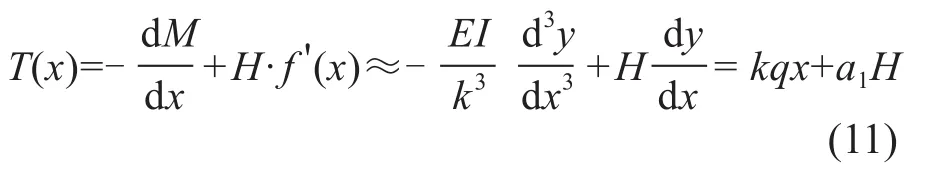
工程中的軟導線多為絞線，將絞線近似看作一“束”子導線構成的集合體，忽略子導線間的摩擦，則軟線的截面系數(shù)的計算方法如下[8-9]：

式中：n為絞線中包含的子導線根數(shù)；r為子導線的半徑，m。

3 算例

根據(jù)上文的推導結果，下面給出幾個工程實例做計算。

1)某110 kV設備連線，相關計算輸入及計算結果見表1。

表1 某110 kV設備連線計算結果

2)某220 kV設備連線，相關計算輸入及計算結果見表2。

表2 某220 kV設備連線計算結果

3)某500 kV設備連線，相關計算輸入及計算結果如表3～表5所示。

表3 金具角度與導線自然彎曲角度相反時設備連線計算結果

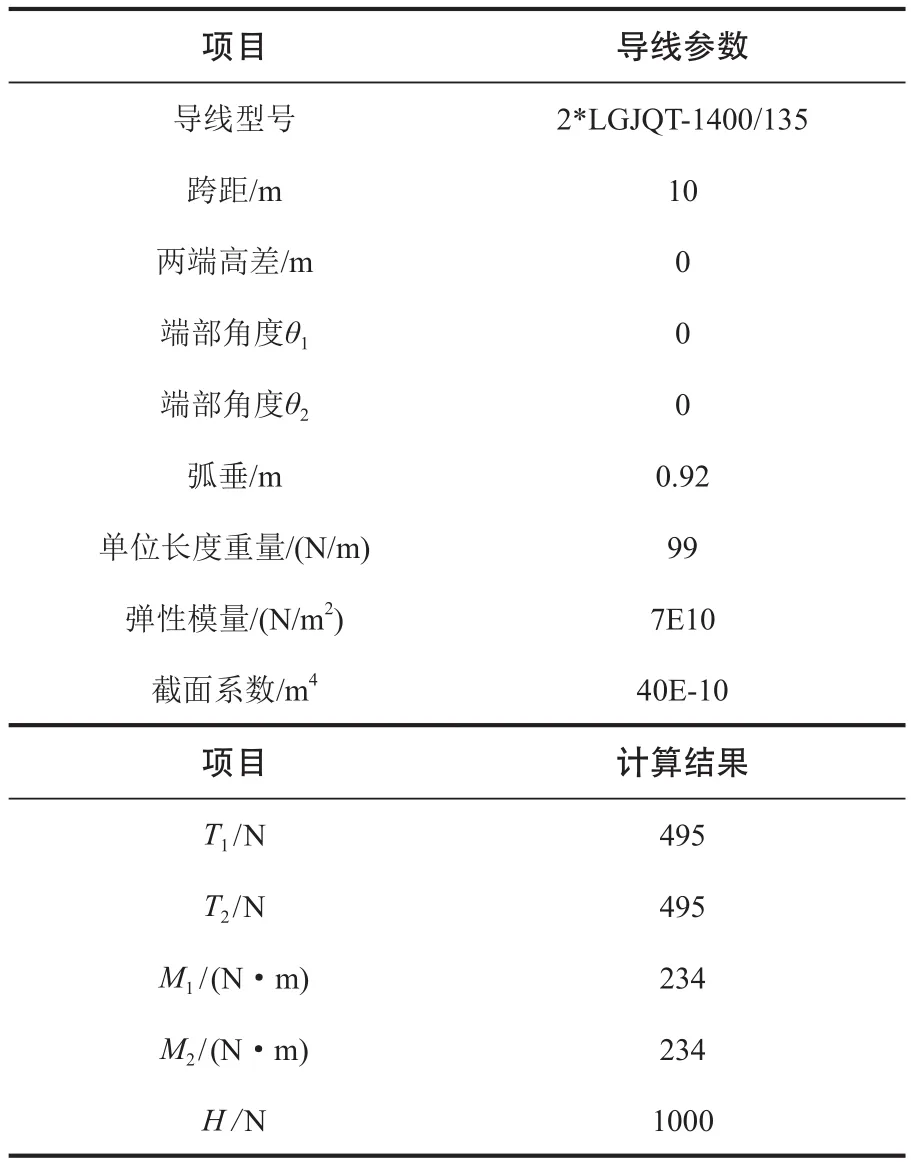
表4 金具角度為零度時設備連線計算結果

表5 金具角度與導線自然彎曲角度相同時設備連線計算結果

由表1～表5可以看出，導線端部的力矩隨著導線重量的增加而增加，隨著導線抗彎強度的增加而增加。

對比表3～表5可以看出，同樣跨度和導線重量下，適當調(diào)整導線端部的角度，使其盡量與導線自然彎曲角度相同，可以明顯降低端部力矩。實際工程中，調(diào)整導線端部的角度可以通過選擇金具的角度來實現(xiàn)。

4 結論

計及軟導線的抗彎強度后，本文推導了軟導線的力學表達式，為一個四階的非線性微分方程。結合工程實際，引入一定的近似條件，本文又將微分方程線性化，并給出了它的解。

通過幾個算例可看出，隨著導線重量和抗彎強度的增加，導線端部的力矩由數(shù)十N·m增大到了數(shù)百N·m；因此在工程設計中，導線端部力矩不應該被忽略處理，而應納入設備的招標規(guī)范中，否則設備端子板有可能被力矩損壞。另外，合理選擇設備端子板連接金具的角度可以有效降低端部力矩。

本文共有兩處近似，在實際應用中會造成一定的誤差：

2)計算軟導線截面系數(shù)時，將其看作一“束”子導線構成的集合體，未考慮子導線絞繞的效果及相互的摩擦力；對于多分裂導線，也未考慮間隔棒的影響。后續(xù)應結合理論和試驗開展軟導線截面系數(shù)的研究。