基于FPGA的高速高效率數字下變頻
戴曜澤,張 棋,徐小淇
(中國航天科工集團8511研究所,江蘇 南京210007)
0 引言
數字下變頻(DDC)的實現主要有2種途徑:1)采用已有的專用DDC芯片;2)采用FPGA或DSP通用芯片直接構建DDC平臺。但專用芯片一般要求數據率小于150 MHz,如AD6620正常工作的數據率小于70 MHz,HSP50016正常工作的數據率小于75 MHz。DSP芯片可高速執行乘累加操作,但只能實現串行操作,在高速并行數據實時處理方面能力較低,故數據處理速率難以滿足使用要求。FPGA芯片可實現并行處理,但由于多個乘法器(DSP48E)級聯造成的線延時和速度限制,難以實現數字下變頻的高速處理,數據率一般不大于400 MHz[1]。
本文基于抽取器的等價原理,對數字下變頻結構進行簡化,可有效解決數據率過高引起的瓶頸問題,極大減少了數字下變頻的計算量和FPGA片內資源消耗,是一種高速高效的數字下變頻的實現結構。
1 數字下變頻結構
1.1 數字下變頻基本結構
數字下變頻基本結構是將中頻信號轉換為基帶信號,基帶信號的正交性由數控振蕩器(NCO)本振來保證,經下變頻后的數字基帶信號處于嚴重的過采樣狀態,經過下變頻濾波后抽取處理[2],其結構如圖1所示。

圖1 數字下變頻基本結構
圖1中,x(n)為經過A/D采樣的數字中頻信號;cos(ω0n)、sin(ω0n)為NCO生成的正交信號;LPF代表低通濾波器,濾除x(n)與NCO混頻的高頻信號;ZI(n)、ZQ(n)為經過D倍抽取的I、Q2路基帶信號。數字下變頻I路輸出[3]ZI(n)可表示為:
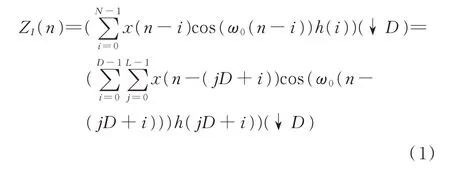
式中,x(n-i)為x(n)延時i的輸出;cos(ω0(n-i))為NCO第n-i時刻的輸出,其中ω0=2πf0/fs,f0為信號的中頻頻率,fs為信號的采樣頻率;h(i)為濾波器的第i個系數;N為濾波器的階數;L=N/D為每個通道濾波器階數。
在工程實現中,為提高系統信噪比,需進行信號的高速采樣,造成中頻數據處理速率低;為了降低數字信號處理數據量,需進行數據抽取操作,過高的抽取倍數會導致很高的濾波器階數,造成大量資源消耗[4]。為了解決速度和資源問題,本文提出了一種數字下變頻改進結構。
1.2 數字下變頻改進結構
根據抽取器的對等關系[5]與式(1)對應的數字下變頻基本型I通道的等效結構如圖2所示。
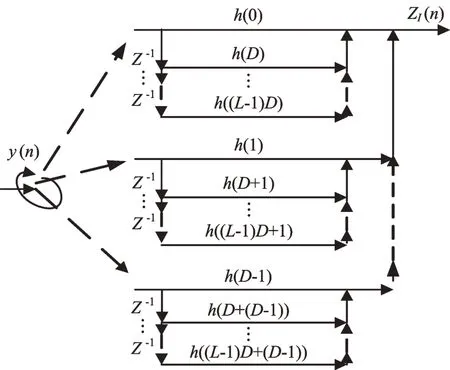
圖2 數字下變頻基本型I通道的等效結構
在圖2中,y(n)表示為:

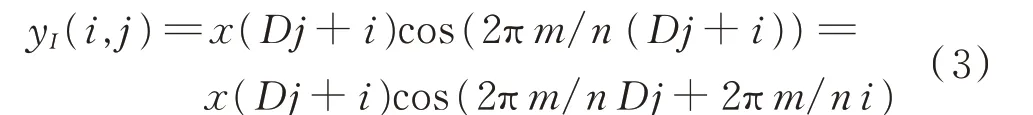
當抽取倍數D為n的整數倍時,則式(3)可簡化為式(4),其對應的數字下變頻改進型I通道結構如圖3所示。
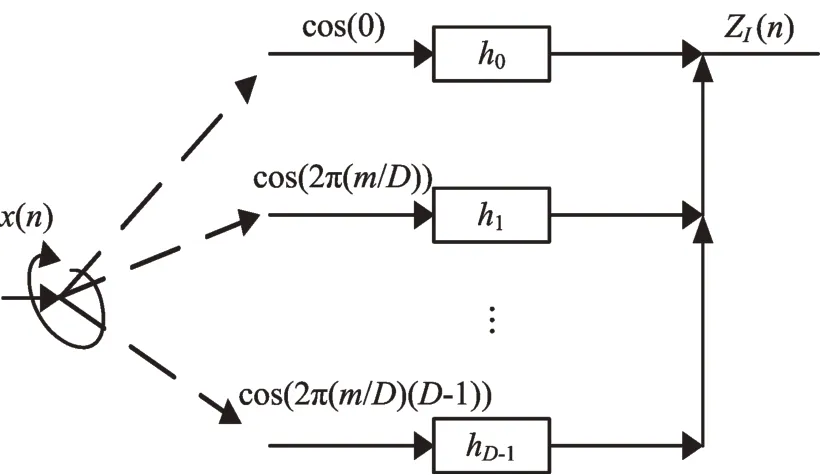
圖3 數字下變頻改進型I通道結構(D為n的整數倍)
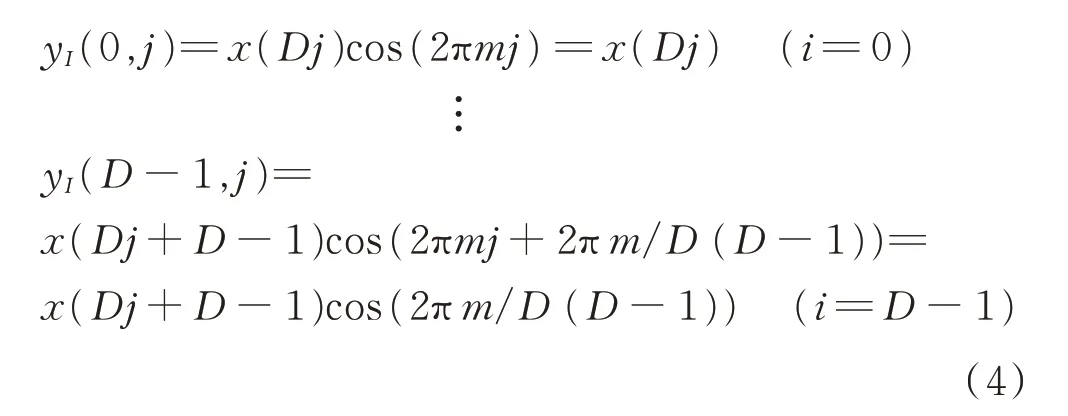
當抽取倍數D為n/2的奇數倍時,則式(3)可簡化為式(5),對抽取數據對2取模,余數為0時數據不變;為1時數據取反,其對應的數字下變頻改進型I通道結構如圖4所示。
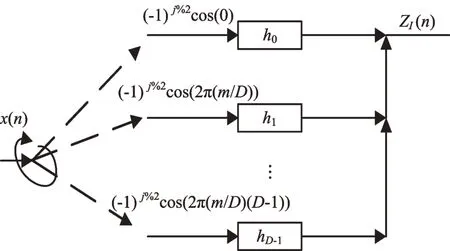
圖4 數字下變頻改進型I通道結構(D為n/2的奇數倍)
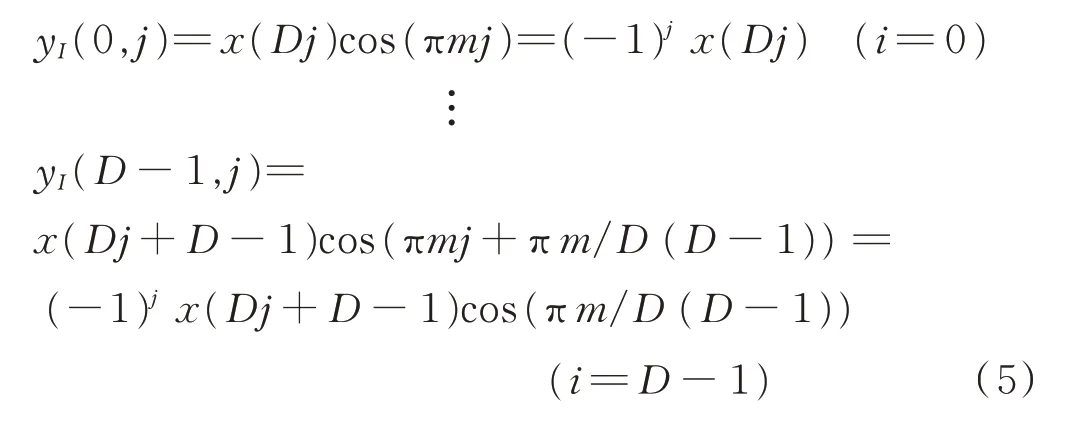
由圖3—4可知,與數字下變頻基本結構相比,數字下變頻改進結構在濾波器前抽取,使數據量降低到原有的1/D,并將串行數據流轉換為并行數據流,從而使系統數據處理速率提高D倍。
綜上所述,在數字下變頻結構設計時,需統籌考慮濾波器階數N、數字中頻頻率f0、抽樣頻率fs以及抽樣倍數D,使得抽樣倍數D滿足上述2個條件,從而選擇相應的數字下變頻改進結構。
2 數字下變頻改進結構工程實現
2.1 Matlab仿真
假設輸入信號x(n)為中頻頻率f0=50 MHz,帶寬B=1 MHz的窄帶信號。根據中頻采樣定理fs≥2B及1.2節所述可知采樣頻率滿足式(6),可采用數字下變頻改進結構設計實現中頻信號到基帶信號的轉換。
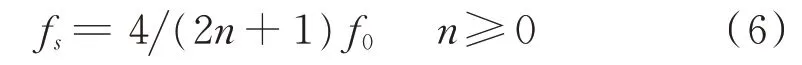
假設n=0,則fs=4f0=200 MHz,抽取倍數D為4滿足中頻采樣定理。
假設數字下變頻低通濾波器的窗函數為凱塞窗,則濾波器階數N為:

式中,δp為通帶紋波系數,取90 d B;δa為阻帶紋波系數,取90 d B;fa為阻帶起始頻率,取2.66 MHz;fc為通帶截至頻率,取1 MHz。由式(7)可知,濾波器階數N為64階。
基于以上參數進行Matlab仿真,數字下變頻基本結構和改進型結構I通道的Matlab仿真結果如圖5所示。

圖5 數字下變頻基本型和改進型I通道Matlab仿真結果
由圖5可看出,數字下變頻的基本結構和改進型結構的時域及頻域的輸出結果是一致的,因此該改進型結構可完全代替數字下變頻的基本結構。
2.2 FPGA實現
基于Matlab仿真結果,4倍抽取倍數的數字下變頻改進結構的FPGA實現框圖如圖6所示。
FPGA芯片采用Xilinx公司的XC4VSX55(速度為-10),數字下變頻基本結構和改進結構濾波器達到的最高時鐘速率分別為222.561 MHz和247.610 MHz。在改進結構中,抽取倍數D為4,其數據處理速率可達到時鐘的4倍,因此數字下變頻改進結構可支持約900 MHz的數據率,從而解決中頻數據處理速率低的問題。
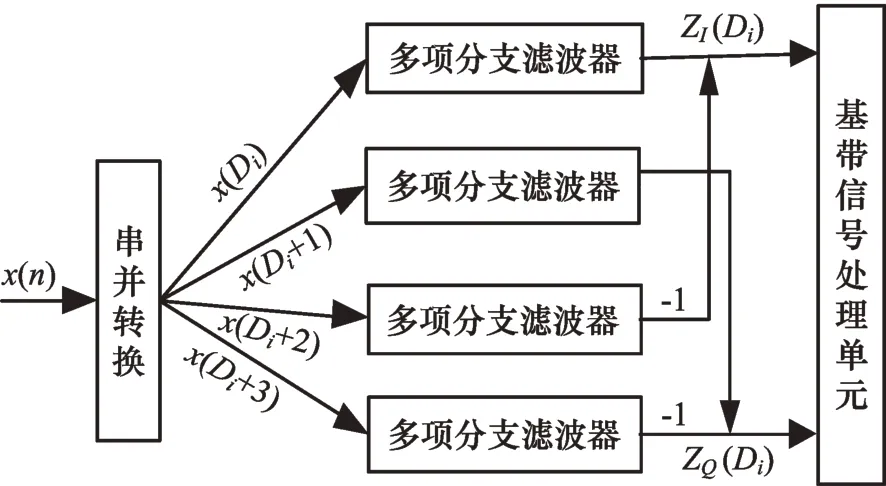
圖6 4倍抽取倍數的數字下變頻改進結構FPGA實現框圖
采用VHDL語言對數字下變頻基本結構和改進結構進行FPGA軟件實現,并采用Modelsim進行仿真,仿真結果如圖7和圖8所示。圖中counter_out代表時延計數,out_i代表數字下變頻I通道的輸出。將圖7、圖8與圖5比較可得,FPGA仿真結果與Matlab仿真結果一致,但數字下變頻基本結構的FPGA實現存在40個時鐘周期時延,而改進型結構僅存在24個時鐘周期的時延,因此數字下變頻改進結構的數據響應時間較快。

圖7 數字下變頻基本結構的FPGA仿真
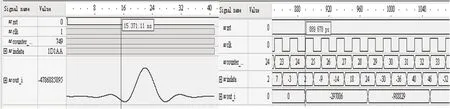
圖8 數字下變頻改進結構的FPGA仿真
數字下變頻基本結構和改進結構的FPGA芯片資源消耗分別如圖9和圖10所示。可以看出,改進型結構消耗的資源僅為基本型結構的1/4左右,在很大程度上降低了資源消耗,解決了FPGA片內資源問題。
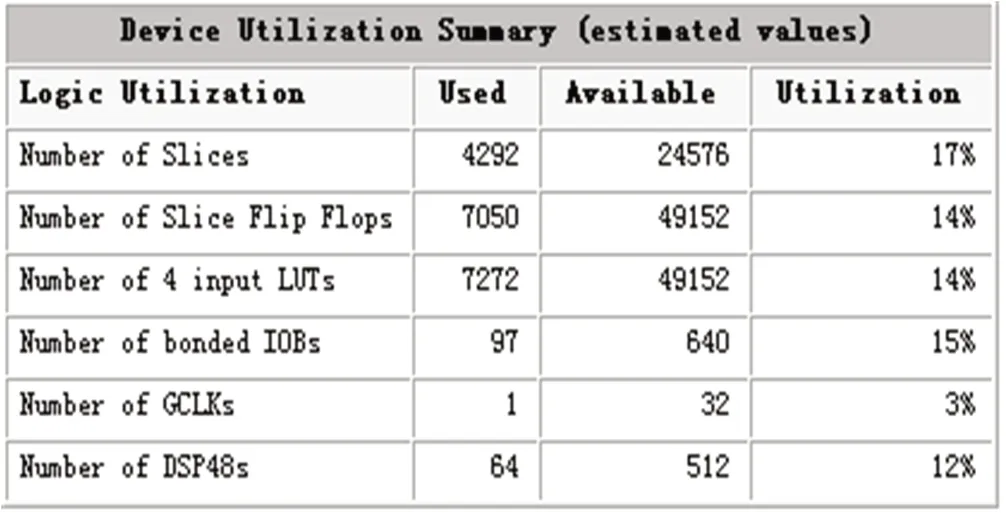
圖9 數字下變頻基本型FPGA資源消耗

圖10 數字下變頻改進型FPGA資源消耗
3 結束語
本文針對數字接收機數字下變頻基本結構數據處理速率低、數據響應速度慢及資源消耗大等問題,提出了一種高速高效的數字下變頻改進結構。該結構利用抽取器的等價原理,對數字下變頻結構進行簡化,并通過FPGA工程實現,具備數據處理速率快、數據響應速度快及資源消耗小等優點,具有很好的實用價值和應用前景。

