C4.5算法在計算機等級考試管理中的應用
鄭秀月
(福州黎明職業技術學院,福建 福州 350001)
1 C4.5算法介紹
C4.5算法是決策樹技術中較為典型的、應用廣泛的分類算法,是ID3算法的提出者J.R Quinlan根據ID3算法存在的一些問題提出的一種改進算法[1]。C4.5不僅具備ID3算法的所有優點,還可以處理離散類型、連續類型的屬性;在生成決策樹時,可以采用邊構造樹邊剪枝或者完整的樹生成之后再進行剪枝的策略,也可以采用不同的剪枝技術如刪除子樹或結點的方法來避免生成不平衡的樹[2]。
2 C4.5算法的改進
2.1 C4.5算法的不足
C4.5算法中,在生成決策樹的過程中需要花大量的時間進行信息增長率的運算,對決策樹的生成效率產生了很大的影響。它與ID3算法一樣仍然是基于“貪心”策略的搜索方式,通過找到每棵子樹的最優解,然后構造出一棵完整的決策樹,這樣只能保證子樹是最優的,最后生成的決策樹未必能達到整體最優。
2.2 C4.5算法的改進
在C4.5算法中,計算分類及測試屬性的信息量時,涉及了對數運算,在進行數據挖掘時要反復地調用對數庫函數,造成計算復雜度大,時間成本高等問題。這里,針對信息量的計算方法提出了改進措施。
假設在樣本數據中,類“YES”的有m個,類“NO”的有n個,則該樣本分類屬性的信息量計算方法如公式(1-1)所示。
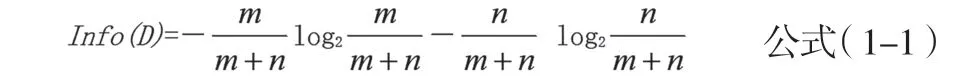
以A為測試屬性,假設A有p個不同的取值,則它的信息量計算方法如公式(1-2)所示。
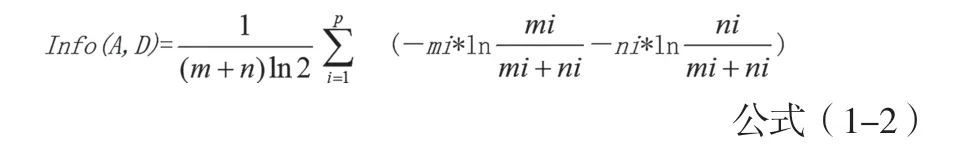
根據高等數學中的泰勒公式、麥克勞林公式和等價無窮小的思想,可以知道當x很小時,ln(1+x)≈x,因此可以得出如下公式(1-3)和公式(1-4)所示。


將公式(1-3)和(1-4)代入公式(1-2)可得如下公式(1-5)所示。

計算時,將公式(1-5)中的常數省略,得出如下公式(1-6)所示。

又因為屬性A對D的分裂信息量計算方法如公式(1-7)所示。

因此可以得出信息增益率如下公式 (1-8)所示。

3 利用改進的C4.5算法生成計算機等級考試成績的決策樹模型
3.1 確定數據挖掘對象和目標
以福州某職業院校2019~2020學年計算機二級等級考試成績為研究對象,隨機抽取了1 100名學生的成績。同時設計了一份問卷調查。希望對這兩份表格的分析挖掘,從中找出影響學生成績的因素,對今后教學工作的開展起到積極的指導作用。
3.2 數據采集
共收集了3張表格數據,分別為學生成績表、平時作業情況表和問卷調查表。其中學生成績表由準考證號、姓名、性別和成績等字段組成,數據由學院的教務處提供,成績為計算機二級等級考試成績。平時作業完成情況表由準考證號、姓名、性別和平時上機作業完成情況等字段組成,數據由任課教師根據學生平時完成實驗的情況給出的統計表。問卷調查表由準考證號、姓名、對該門課程的興趣度、原有知識水平程度和課后復習鞏固時間等字段組成。
3.3 數據預處理
上述所收集的數據如果直接用于挖掘工作,會直接影響挖掘的結果,因此要對收集到的原始數據進行數據清理、數據表合成、數據轉換和數據降維等預處理。在數據轉換中將連續型的成績數據轉換為離散型的數據類型,將“成績”一欄用“是否通過”來標識,結果顯示“通過”或“未通過”。在數據降維中刪除對挖掘結果不產生影響的字段“姓名”和“性別”,保留能唯一標識一條記錄的字段“準考證號”即可。預處理后最終生成的數據表如下表1-1所示。
3.4 構造成績“未通過”的決策樹模型
為了找出影響學生計算機等級二級考試成績不及格的因素,因此將表1-1中的成績“未通過”的記錄提取出來組成新的表格來建立決策樹:

表1 -1 學生成績分析表
3.4.1 計算每個屬性的信息量
在成績“未通過”的學生成績分析表,與“未通過”相關的屬性有“對該門課程的興趣度”、“原有知識水平程度”“平時上機作業完成情況”和“課后復習鞏固時間”。根據公式1-6分別求出每個屬性的信息量。
(1)計算屬性“對該門課程的興趣度”的信息量,該屬性共有三個屬性值,分別為“感興趣”“不感興趣”和“一般”,其樣本數分別為:“感興趣”的有305個,“不感興趣”的有245個,“一般”的有400個。
“感興趣”的305個樣本中,類“YES”的有215個,類“NO”的有90個,可以表示為(215,90),其信息量:
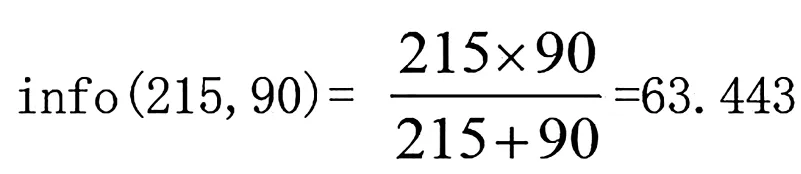
同理計算“不感興趣”的245個樣本中,其信息量info(0,245)=0;
“一般”的400個樣本中,其信息量info(175,225)=98.4375;
因此,屬性“對該門課程的興趣度”的信息量
info(興趣度,D)=63.443+98.4375=161.8805
(2)計算屬性“課后復習鞏固時間”的信息量,該屬性“大于2小時”“1-2小時”和“小于1小時”對應的樣本數分別為165、340和445,分別計算他們的信息量為info(45,400)=40.449、info(200,140)=82.353、info(145,20)=17.576;
因此,屬性“課后復習鞏固時間”的信息量為:40.449+82.353+17.576=140.378
(3)計算屬性“原有知識水平程度”的信息量,該屬性共有三個屬性值,其對應的樣本數分別為:“好”的有275個,“中”的有395個,“差”的有280個,分別計算他們的信息量為info(205,70)=52.182、info(160,235)=95.190、info(25,255)=22.77;
因此,屬性“原有知識水平程度”的信息量為:52.182+95.190+22.77=170.142
(4)計算屬性“平時上機作業完成情況”的信息量,該屬性共有三個值,其對應的樣本數分別為:“優”的有305個,“良”的有330個,“差”的有315個。別計算他們的信息量為info(290,15)=14.26、info(100,230)=69.697、info(2,315)=1.9873
因此,屬性“平時上機完成情況”的信息量為:14.26+69.697+1.9873=85.9443
3.4.2 根據公式1-7計算每個屬性的分裂信息量
屬性“對該門課程的興趣度”的分裂信息量為:

依次分別算出屬性“課后復習鞏固時間”“原有知識水平程度”“平時上機作業完成情況”的分裂信息量分別為:26278.421、32015.789、33373.421。
3.4.3 根據公式1-8計算各屬性的信息增益率
屬性“對該門課程的興趣度”的信息增益率為:

依次分別算出屬性“課后復習鞏固時間”“原有知識水平程度”“平時上機作業完成情況”的信息增益率分別為:0.99465、0.99468、0.99742。
3.4.4 選取信息增益率最大的屬性作為決策樹的根結點
綜上所述,“平時上機作業完成情況”屬性具有最大的信息增益率。因此將其作為測試屬性,用“平時作業”來標識,并對每個屬性值建立分支生成的決策樹。同理,對于各個分支節點用以上的方法進一步進行劃分,生成完整的決策樹
3.5 決策樹的剪枝
決策樹的剪枝,就是在單個葉子結點的期望錯誤率低于相應子樹結點的期望錯誤率時,用該葉子結點來代替一整棵子樹[3]。目前,常用的決策樹剪枝算法主要有兩種即先剪枝方法和后剪枝方法[4],對上述已生成的完整決策樹模型采用了“后剪枝”的方法,通過剪枝后生成的決策樹如下圖1所示。
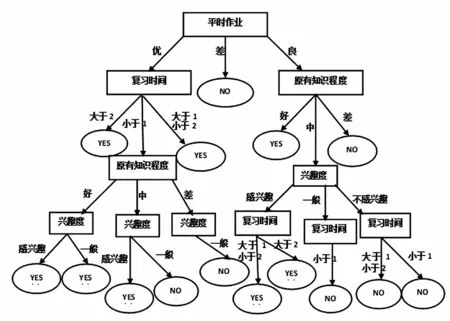
圖1 決策樹
3.6 生成規則
決策樹算法很重要的一個優點就是能夠直接生成以IF……THEN……語句的形式表示的規則,而且這種形式表示的規則易于被人們理解和接受[5]。從上面決策樹中提取的成績為“未通過”的規則有:
IF“平時作業”=“優”AND“復習時間”=“小于1”AND“原有知識程度”=“中”AND“興趣度”=“一般”THEN“成績是否通過”=“未通過”;
IF“平時作業”=“優”AND“復習時間”=“小于1”AND“原有知識程度”=“差”AND“興趣度”=“一般”THEN“成績是否通過”=“未通過”;
IF“平時作業”=“良”AND“原有知識程度”=“中”AND“興趣度”=“一般”AND“復習時間”=“小于1”THEN“成績是否通過”=“未通過”;
IF“平時作業”=“良”AND“原有知識程度”=“中”AND“興趣度”=“不感興趣”AND“復習時間”=“小于1”THEN“成績是否通過”=“未通過”;
IF“平時作業”=“良”AND“原有知識程度”=“中”AND“興趣度”=“不感興趣”AND“復習時間”=“大于1小于2”THEN“成績是否通過”=“未通過”;
IF“平時作業”=“差”THEN“成績是否通過”=“未通過”;
IF“平時作業”=“良”AND“原有知識程度”=“差”THEN“成績是否通過”=“未通過”;
從以上得出的分類規則可以看出,“平時上機作業完成情況”對考試是否通過影響很大。“課后復習鞏固時間”也在很大程度上影響著考試是否通過。因此,教師在教學過程中要注重學生的實際動手能力,對學生“平時上機作業完成情況”要即時的進行講評、反饋,即時解決學生在上機過程中遇到各種問題。同時要督促學生課后多花時間進行復習鞏固,加深印象,以此來提高等級考試的通過率。
3.7 挖掘結果的評估
將以上生成的學生成績是否通過的決策樹模型應用于預留的用于測試的90條記錄,發現90條記錄中,利用圖3-1的決策樹對學生成績是否通過進行預測,發現錯誤的條數為5條,即正確率達到了94.4 %。同理分別對19級計算機專業和19級藝術設計專業的成績進行測試,正確率分別達到了93.2 %和95.2 %。
經過測試,發現以上所生成的決策樹模型效果良好。
4 結語
本文主要運用改進的C4.5算法建立了學生成績是否通過的決策樹模型,產生分類規則并對挖掘結果進行了評價,分析了影響國家計算機二級等級考試通過率低的因素,以幫助教師更好地進行教學活動,提高等級考試的通過率。

