不倒塔的實驗探究

李可妤，徐 蕾，鐘 鳴

(南京師范大學(xué) 物理科學(xué)與技術(shù)學(xué)院，江蘇 南京 210023)

在演示平衡和慣性的實驗中，有一類非常有趣的實驗，例如，把硬幣一個個疊起，看看誰能使疊的硬幣伸出底面最多？把硬幣堆疊成直立的塔，快速擊打最下層的硬幣，看看誰能保證上層的塔不倒？在有趣的實驗現(xiàn)象和定性解釋背后，保持平衡的條件究竟和哪些因素有關(guān)，值得更為深入的探討. 為此，設(shè)計了不倒塔的實驗裝置，通過實驗進行定量探究.

1 實驗設(shè)計與原理

1.1 實驗裝置設(shè)計

首先搭建整體裝置，把幾個相同的圓盤上下整齊地疊放在桌面上，形成直立的塔. 考慮到直接擊打較難準確控制力的大小、方向以及作用時間，采用了替代方法：將輕繩一端連接重物瓶，穿過定滑輪后連接到最底層的圓盤上,如圖1所示.

圖1 實驗裝置示意圖

通過突然釋放重物瓶來等效替代擊打最底層的圓盤，可以通過改變重物瓶的質(zhì)量以改變突然施加的水平力的大小，降低測量的難度，保證可重復(fù)性.

1.2 實驗現(xiàn)象

在實驗中可以觀察到，當(dāng)塔層形狀相同時，改變瓶中重物的質(zhì)量會影響最下層塔抽出的時間，進而影響塔是否能夠保持直立不倒. 當(dāng)外加水平力越大，抽取時間越短，上方的塔身受到的影響就越小，塔越能保持穩(wěn)定.

以地面為參考系，建立二維平面xy坐標系，其中x方向為水平方向，y方向為豎直方向. 標記每層塔的中心位置，拍攝實驗視頻，采用Tracker軟件記錄數(shù)據(jù)，對層數(shù)為4的塔的整體運動情況進行分析.

圖2為各圓盤的x和y方向的位移隨時間的變化情況. 由圖2可以看出，在x方向上，同一塔中各個圓盤最終會發(fā)生錯位，低層的圓盤x方向的位移更大；在y方向上，曲線前段較光滑部分表示自由下落過程，后由于碰撞地面引起微小擾動.

1.3 原理分析

將最下面的圓盤稱為底層圓盤,上面的圓盤整體稱為塔身，并且對塔身的每個圓盤從下到上進行編號1，2…N. 將塔的運動過程分為3個階段：接觸階段、自由下落階段和碰撞階段，接下來將分階段描述塔的運動情況.

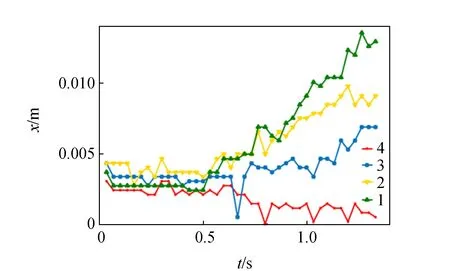
(a)x方向位移

(b)y方向位移圖2 x和y方向塔的整體運動情況圖

1.3.1 接觸階段

接觸階段從突然施加的水平力作用于底層圓盤開始，到塔身脫離最底層圓盤結(jié)束，構(gòu)成塔身的圓盤彼此之間沒有相對位移，塔身可視為剛體. 這一階段又分為2個過程，如圖3所示.

(a) (b)圖3 接觸階段示意圖

1)當(dāng)?shù)讓訄A盤與塔身脫離距離小于圓盤半徑R，塔身不發(fā)生傾斜. 底層圓盤受到的力有重力、塔身給予的摩擦力與壓力、桌面給予的支持力與摩擦力；塔身受到的力有重力、底層圓盤給予的支持力與摩擦力.

底層圓盤的水平方向運動方程為

(1)

塔身作為整體(剛體)的運動方程為

(2)

其中，m為單個圓盤的質(zhì)量，R為圓盤半徑，M為懸掛重物的質(zhì)量，x底為底層圓盤的x方向位移，x塔為塔身的x方向整體位移，μ為圓盤與圓盤之間的摩擦因數(shù)，μ0為底層圓盤與桌面的摩擦因數(shù).

2)當(dāng)?shù)讓訄A盤與塔身脫離距離大于半徑R，此時塔身會繞著接觸點進行轉(zhuǎn)動. 在實驗過程中，傾斜角度較小，并且這一過程持續(xù)時間較短，因此，可以近似認為底層圓盤的受力恒定，此時底層圓盤的運動方程仍為式(1)，塔身的運動為平動與繞接觸點的轉(zhuǎn)動的合成，平動的運動方程仍為式(2). 繞接觸點的轉(zhuǎn)動方程為[1]

(3)

其中，J為轉(zhuǎn)動慣量，θ為傾斜角度，h為單個圓盤高度，其值為

(4)

其中Δx表示接觸點到塔身底邊中點的距離，滿足以下條件：

(5)

1.3.2 自由下落階段

自由下落階段如圖4所示，從塔身與地面脫離為開始，到塔身觸碰地面結(jié)束. 塔身只受到重力作用，作為整體進行運動. 將這一運動進行分解，可以分為質(zhì)心的拋體運動與整體繞質(zhì)心軸的轉(zhuǎn)動. 并且轉(zhuǎn)動的初始角速度ω來自接觸階段，在自由下落階段，質(zhì)心軸合力矩為0，因此是角速度為ω的勻角速轉(zhuǎn)動. 用Δy表示圓盤下端離地面的豎直距離，滿足以下方程：

圖4 自由下落階段示意圖

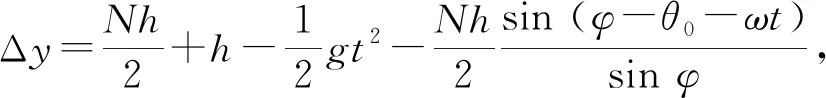
(6)

其中，θ0為初始傾斜角度，φ為其余圓盤的對角，即

(7)

1.3.3 碰撞階段

碰撞階段從塔身接觸地面開始，到塔身部分的各個圓盤相對地面靜止結(jié)束. 由于碰撞等復(fù)雜的運動，最后塔身部分的各個圓盤會在x方向上產(chǎn)生錯位，如圖5所示. 當(dāng)圓盤間相對位移在一定范圍內(nèi)，塔不會倒塌；當(dāng)相對位移超出某一臨界值時，塔會倒塌. 而關(guān)于這一臨界判斷條件，將在后面進行討論.

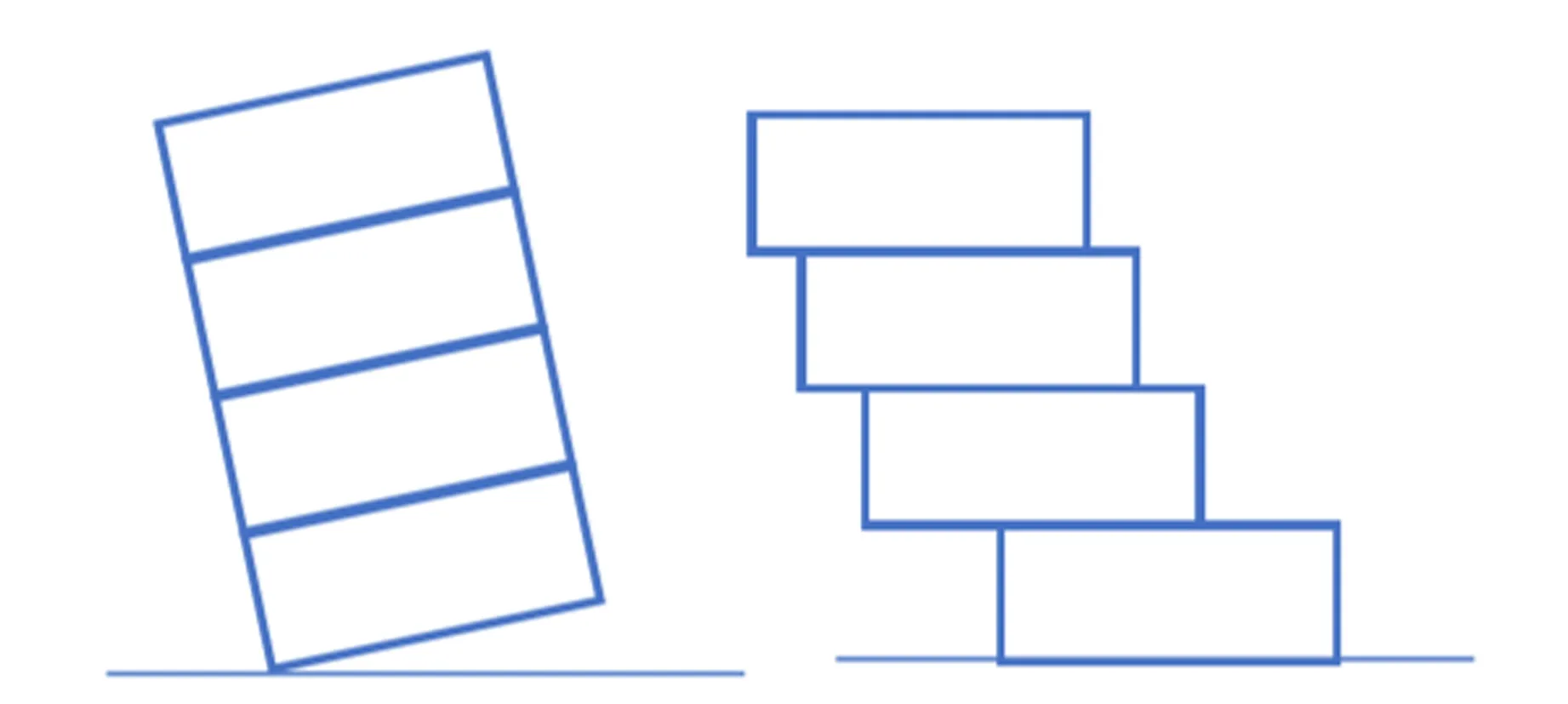
(a)碰撞地面 (b)最終狀態(tài)圖5 碰撞階段示意圖

碰撞階段初始時的各個圓盤的速度：

(8)

(9)

其中，θ落為塔身剛落到地上的傾斜角度，n為第n個圓盤的編碼，N為塔身的總圓盤個數(shù).vx，vy分別為整體運動時質(zhì)心的速度，經(jīng)歷前2個階段之后其值分別為

(10)

vy=gt階段2,

(11)

碰撞到地面后，各個圓盤的速度與碰撞系數(shù)有關(guān)[2]：

vny=vny初[en-1e0-eN-n],

(12)

(13)

其中，e為圓盤之間的碰撞系數(shù)，e0為圓盤與地面間的碰撞系數(shù).

自接觸地面開始，各圓盤均以下端接觸地面的點為轉(zhuǎn)軸，完全落地后可認為傾斜角度約等于落地瞬間整體的傾角，各層圓盤在x方向產(chǎn)生的位移為

(14)

與地面碰撞后x方向產(chǎn)生位移為

(15)

落地后僅有x軸方向的運動，塔層間相互鎖定，受摩擦力作用直到vnx=0,

(16)

圓盤之間最終的相對位移為[3]：

xn=xn1+xn2+xn3.

(17)

1.3.4 塔是否倒塌的判據(jù)

顯然，當(dāng)圓盤間相對位移在一定范圍內(nèi)，塔不會倒塌；當(dāng)相對位移超出某一臨界值時，塔會倒塌. 接下來根據(jù)堆塔原理(圖6)建立塔是否倒塌的判斷函數(shù)[4-8].

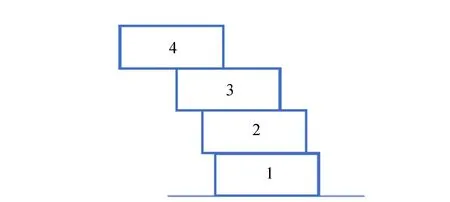
圖6 堆塔原理示意圖

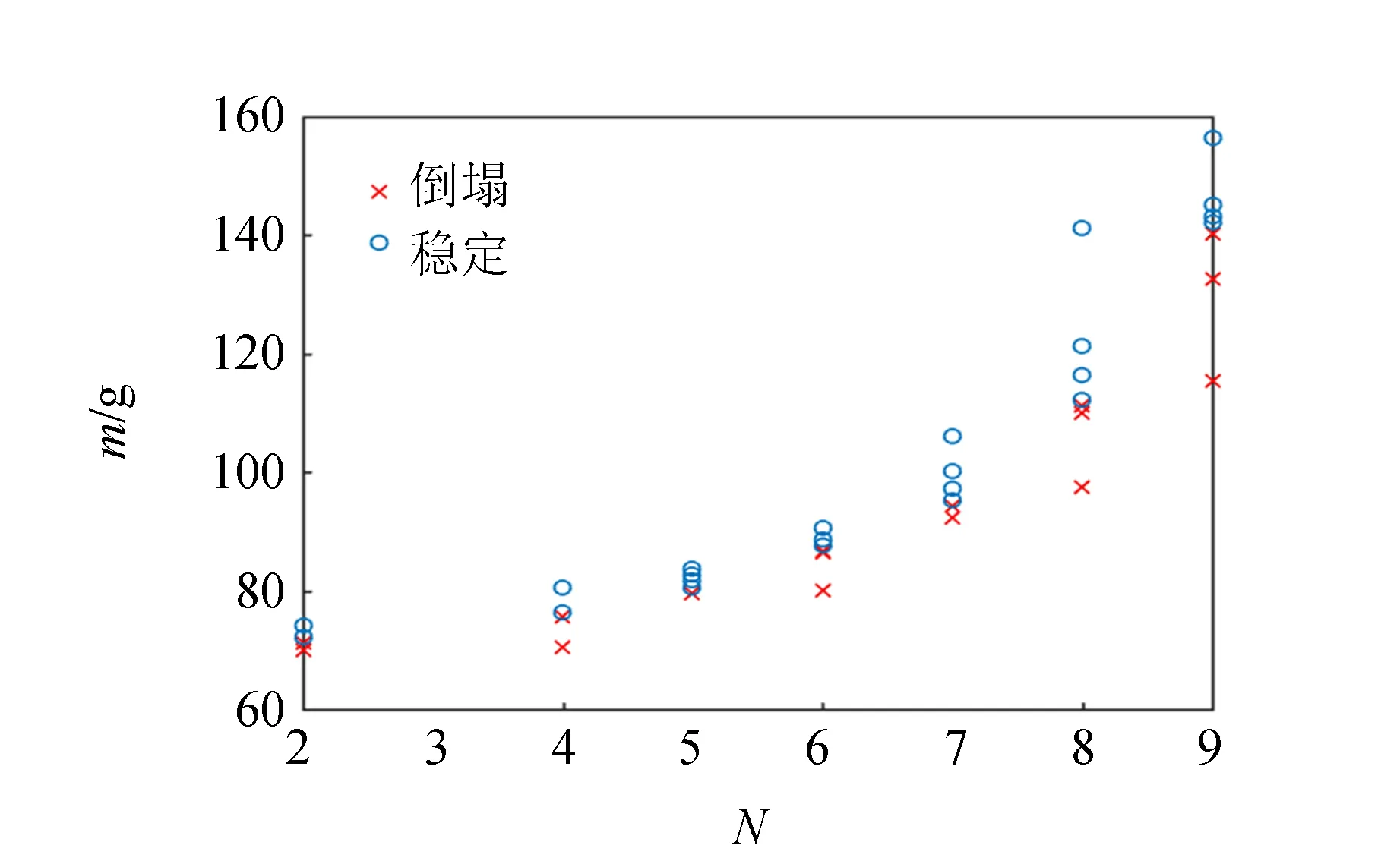
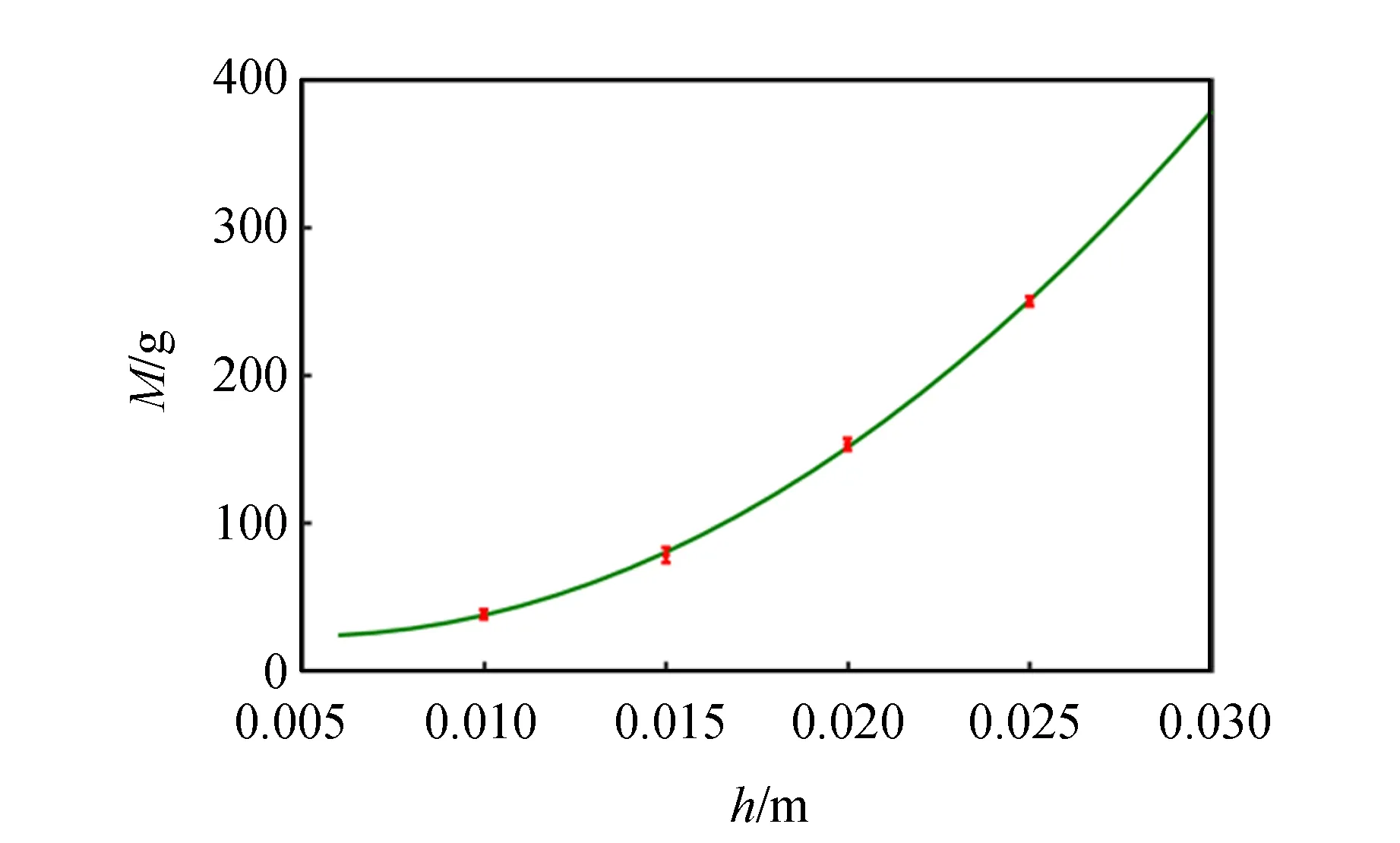
xcN-n-xn

(18)

(19)

同時滿足這2個條件，塔不會倒塌.

通過以上分析，可以用Matlab對運動的3個階段進行數(shù)值模擬，最終將實驗結(jié)果和數(shù)值模擬結(jié)合，得到相關(guān)參量和塔穩(wěn)定性之間的關(guān)系.

2 實驗探究

2.1 實驗器材

器材包括電子天平、定滑輪、魚線、重物瓶、小圓珠、不同規(guī)格的亞克力圓盤以及不同粗糙程度的磨砂紙，如圖7所示.

(a)實驗裝置 (b)不同規(guī)格的亞克力圓盤圖7 實驗器材圖

2.2 對影響塔穩(wěn)定性相關(guān)參量進行實驗探究

根據(jù)上述理論分析，設(shè)計了一系列控制變量實驗，分別改變圓盤的層數(shù)N、圓盤的半徑R、單個圓盤的高度h、圓盤與地面間的摩擦因數(shù)μ0以及圓盤間的摩擦因數(shù)μ，探究影響塔保持直立的條件，如圖8所示.

圖8 相關(guān)參量圖例

2.2.1 圓盤層數(shù)N和塔穩(wěn)定性的關(guān)系

采用R=1.5 cm，h=1.5 cm的圓盤進行實驗，其他條件不變，改變圓盤的層數(shù). 可以看出隨著塔層數(shù)的增加，需要施加懸掛物的臨界質(zhì)量呈上升趨勢. 即層數(shù)越大，所需懸掛物的質(zhì)量越大才能保證塔不倒塌，層數(shù)越高的塔越不穩(wěn)定. 在實驗中還發(fā)現(xiàn)，當(dāng)N=7時，所需懸掛物的臨界質(zhì)量會驟然增加，這是由于層數(shù)的增大，圓盤間的相互影響會導(dǎo)致更大的不穩(wěn)定性.

圖9(b)中綠線為Matlab模擬的結(jié)果，取0.01為步長，通過數(shù)值計算得到臨界的質(zhì)量，與實驗進行對比，可以看出模擬和實驗結(jié)果符合得很好. 而對于任意一組控制變量實驗，使用的懸掛物的質(zhì)量最小為1.5 g，通過不斷增加懸掛物的質(zhì)量來尋找能夠使塔不倒的臨界質(zhì)量.

(a)實驗結(jié)果圖

(b)模擬和實驗對比圖圖9 圓盤層數(shù)和塔穩(wěn)定性關(guān)系

2.2.2 圓盤的半徑R和塔穩(wěn)定性的關(guān)系

采用層數(shù)為4層，h=1.5 cm的圓盤進行實驗，其他條件不變，改變圓盤的半徑R,實驗曲線如圖10所示. 實驗發(fā)現(xiàn)，當(dāng)圓盤半徑在一定范圍內(nèi)時，圓盤的半徑越大，需要施加懸掛物的臨界質(zhì)量呈下降趨勢，即半徑越大塔越穩(wěn)定；但當(dāng)半徑超過某一臨界值時，抽出底層圓盤的位移變大，抽出時間也會越長，需要施加懸掛物的臨界質(zhì)量呈上升趨勢，塔越難以保持直立，穩(wěn)定性越差. 也就是說圓盤存在最優(yōu)半徑，模擬結(jié)果顯示其最優(yōu)值為2.15 cm. 當(dāng)半徑超過最優(yōu)值時，其余圓盤與底部圓盤的的接觸時間增加，其獲得的角速度與傾斜角度增大，塔難以保持直立.

圖10 圓盤半徑和塔穩(wěn)定性關(guān)系的模擬和實驗對比圖

2.2.3 單個圓盤高度h和塔穩(wěn)定性的關(guān)系

采用層數(shù)為4層，R=1.5 cm的圓盤進行實驗，其他條件不變，改變圓盤的高度h，實驗圖像如圖11所示. 可以看出隨著單個圓盤高度的增加，需要施加懸掛物的臨界質(zhì)量呈上升趨勢. 即單個圓盤高度越高的塔越不穩(wěn)定. 從定性的角度分析，塔重心越高越不穩(wěn)定，因此需要更大的臨界質(zhì)量來縮減對其余圓盤的影響時間.

圖11 單個圓盤高度和塔穩(wěn)定性關(guān)系的模擬和實驗對比圖

2.2.4 圓盤與地面間的摩擦因數(shù)μ0和塔穩(wěn)定性的關(guān)系

控制其余變量不變，僅改變圓盤與地面接觸面的摩擦因數(shù)μ0，實驗圖像如圖12所示. 發(fā)現(xiàn)圓盤與地面間的摩擦因數(shù)μ0越小，所需施加懸掛物的臨界值量就越小，塔穩(wěn)定性越好. 從這一實驗看，地面的摩擦因數(shù)對塔產(chǎn)生的是負影響. 由于摩擦力的增大，為了控制抽取時間，所需的臨界質(zhì)量也會相應(yīng)增大.

2.2.5 圓盤間的摩擦因數(shù)μ和塔穩(wěn)定性的關(guān)系

控制其余變量不變，僅改變上層圓盤間的摩擦因數(shù)μ，實驗圖像如圖13所示. 可以發(fā)現(xiàn)，在一定范圍內(nèi)時，圓盤間的摩擦因數(shù)越大，需要施加懸掛物的臨界質(zhì)量呈下降趨勢；當(dāng)摩擦因數(shù)超過某一臨界值時，需要施加懸掛物的臨界質(zhì)量又會增加. 考慮到摩擦因數(shù)較小，導(dǎo)致在第三階段塔層間相互鎖定時，vnx需要較長時間才能減為0，圓盤間的相對位移反而超過堆塔原理所要求的臨界距離，導(dǎo)致塔更加難以保持不倒.

圖12 圓盤和地面間摩擦因數(shù)和塔穩(wěn)定性關(guān)系的模擬和實驗對比圖

圖13 圓盤間摩擦因數(shù)和塔穩(wěn)定性關(guān)系的模擬和實驗對比圖

3 實驗結(jié)論

從實驗可以得出，塔保持不倒的原因是用突然的水平力抽取底層圓盤后，導(dǎo)致塔身各個圓盤之間產(chǎn)生相對位移,當(dāng)相對位移處在堆塔原理限制的塔層間最大伸出距離以內(nèi)，塔可以保持直立.

采用模擬與實驗相結(jié)合的方法，從影響塔的穩(wěn)定性的因素出發(fā)，探究了塔的保持直立的條件，得到主要結(jié)論如下：

1)不利的影響因素有塔的層數(shù)、單個圓盤的高度、圓盤與地面的摩擦因數(shù). 塔的層數(shù)越大、圓盤的高度越高、圓盤與地面的摩擦因數(shù)越大，塔越不穩(wěn)定；

2)圓盤的半徑對于塔保持直立的影響存在最優(yōu)的值，這時塔的穩(wěn)定性最好；

3)圓盤間的摩擦因數(shù)對于塔保持直立的影響也不是單一的，在一定范圍內(nèi)時，圓盤間的摩擦因數(shù)越大，塔的穩(wěn)定性越好，當(dāng)超過某一臨界值時，塔越不穩(wěn)定.

4 總結(jié)與反思

本文對一個典型的力學(xué)問題進行探究，通過給底層圓盤施加突然的水平力這一外在客觀表現(xiàn)來觀察塔自身的穩(wěn)定性情況，基本思想是從預(yù)實驗中塔的整體運動規(guī)律出發(fā)→分解各個階段的運動過程→得出最終狀態(tài)圓盤之間橫向位移的關(guān)系→通過判斷函數(shù)得出塔是否能保持直立→正式實驗進行驗證. 實驗采用的描述方法如圖14所示.

圖14 實驗描述方法

本文在實驗理論上進行了一定的簡化，在此僅給出了主要影響參量的實驗結(jié)果，而對于其他的影響因素，如碰撞系數(shù)等，因?qū)嶒灡砻嫠貌馁|(zhì)相同而近似認為碰撞系數(shù)不變，在該實驗中作為無關(guān)變量進行控制.