體外配置CFRP 預應力筋RPC 梁抗彎性能試驗研究

方志，黃正猛，賈理

（湖南大學 土木工程學院，湖南 長沙 410082）

混凝土結構已成為當今世界土木工程中最主要的結構形式，但普通混凝土結構普遍面臨結構自重大、易開裂、耐久性仍顯不足等問題.因此，尋求一種更為有效的配筋混凝土結構以降低結構自重、增強結構耐久性，對土木工程的發展具有重要意義.

基于最大密實度原理配制的活性粉末混凝土（Reactive Powder Concrete，RPC），具有超高的抗壓強度和較高的抗拉強度、良好的韌性、優異的耐久性，熱養護后基本無收縮且徐變大幅降低等特征.RPC也由此被歸于超高性能混凝土范疇并被視為新一代水泥基材料[1-3]，在土木工程中具有良好的應用前景.有關RPC 材料的國家標準《活性粉末混凝土》（GB/T 31387—2015）已頒布實施[4].采用高強RPC 可形成輕薄構件，從而顯著降低結構自重，并大幅提高結構耐久性.

雖然薄腹RPC 梁能顯著增大結構的跨越能力、提高結構抵抗使用荷載的有效性，但較小的壁厚往往導致體內預應力筋難以布置，使得結構尺寸將由構造要求而非受力要求所決定.此時，采用體外預應力結構不失為一種更加合理的選擇.但傳統體外預應力結構中采用的鋼制預應力筋普遍存在耐久性能和抗疲勞性能不足的問題.碳纖維增強復合材料（Carbon Fiber Reinforced Polymer，CFRP）具有強度高、重量輕、免銹蝕及抗疲勞性能好等優點[5-7]，可望成為傳統鋼制體外預應力筋的潛在替代品，并與RPC 一道，形成一種結構性能和耐久性能優良的體外預應力混凝土結構.

國內外學者對RPC 和CFRP 的工程應用研究不斷開展.鞠彥忠等[8]通過對不同鋼纖維摻量RPC 的力學性能試驗研究證明，鋼纖維的摻入可明顯提高RPC 的抗壓強度、劈拉強度和抗折強度；韓菊紅等[9]通過11 根無筋鋼纖維混凝土梁及4 根配筋混凝土梁彎曲抗裂性能的對比試驗，研究了混凝土中鋼纖維對試件受彎性能的影響，結果表明：對以抗裂或限裂為主要控制條件的受彎構件，可用鋼纖維混凝土替代構造配筋混凝土；余自若等[10]對不同配筋率下RPC 矩形梁、T 形梁進行了抗彎試驗研究，表明RPC梁的開裂荷載較普通混凝土高，但無配筋RPC 梁仍表現出“少筋”破壞特點；鄭文忠等[11]通過6 根RPC梁試驗研究了RPC 受彎構件的性能，建立了考慮截面受拉區拉應力貢獻的正截面承載能力計算公式；孟履祥等[12]通過試驗研究了配置AFRP 和CFRP 預應力筋部分預應力混凝土梁的受力性能，結果表明梁具有較好的延性和耗能能力；楊劍、方志[13]對體內配置CFRP 預應力筋RPC 梁的受力性能進行了試驗研究，表明CFRP 預應力RPC 梁具有期望的裂縫分布及破壞形態；Jung 等[14]試驗研究了體外及體內無黏結CFRP 預應力筋普通混凝土梁的抗彎性能，結果表明，跨中設置轉向器的體外CFRP 預應力混凝土梁與體內無黏結CFRP 預應力梁具有相近的受力性能；Grace 等[15]對體外CFRP 預應力筋普通混凝土梁的抗疲勞性能進行了試驗研究，結果表明，經歷700 萬次重復荷載作用后，體外CFRP 預應力筋仍未出現損傷.

總之，目前國內外對普通配筋RPC 結構、體內CFRP 預應力筋普通混凝土結構、體內CFRP 預應力筋RPC 結構以及體外CFRP 預應力筋普通混凝土結構的受力性能均有研究，但對體外配置CFRP 預應力筋RPC 結構受力性能的研究鮮有文獻報導.另外，現有研究認為[16-17]：RPC 中由于高強鋼纖維的作用，使其具有較高的抗拉和抗剪強度，在構件中能夠直接承受較大的拉應力和剪應力，因此對于普通鋼筋RPC 梁和體內預應力RPC 梁，可以取消這兩類梁內的受剪鋼筋和后者體內的普通受拉鋼筋.但此舉對于體外預應力RPC 梁是否合適還有待研究.基于上述兩方面的考慮，本文以剪跨比、張拉控制應力以及預應力度為試驗參數，對4 根體外配置CFRP 預應力筋RPC 梁的抗彎性能進行試驗研究，以期明確這種梁的受力變形特征.

1 試驗概況

1.1 試件設計

共設計了4 根體外配置CFRP 預應力筋RPC 簡支T 梁，如圖1 所示.梁長2.44 m，計算跨徑2.26 m，梁高0.2 m，跨高比為11.3.體外布置2 根直線型CFRP 預應力筋，轉向器設置在梁跨中位置處，與CFRP 預應力筋的接觸面為馬鞍形不銹鋼片，曲率半徑為40 cm.試驗參數為剪跨比、張拉控制應力和預應力度.剪跨比分別為5.65 和2.55，分別對應跨中單點加載及純彎段長度為1 240 mm 的跨內兩點對稱加載.試驗設置不同剪跨比是為了明確梁受彎、受剪裂縫以及有無純彎區時裂縫的分布特征，而非研究梁的抗剪承載能力；預應力筋張拉控制應力σcon分別為0.45ffp和0.55ffp，這里ffp為CFRP 筋的抗拉強度；預應力度PPR（這里定義PPR=Apffp/（Apffp+Asfy），Ap和As分別為CFRP 預應力筋和非預應力受拉鋼筋的面積，ffp和fy分別為CFRP 筋抗拉強度和鋼筋屈服強度）分別為1.0 和0.71，PPR=1.0 為梁內未布置任何普通鋼筋的全預應力梁，PPR=0.71 為梁內受拉區布置了2 根直徑為16 mm 的HRB400 級非預應力普通鋼筋的部分預應力梁.圖1（b）和（c）所示為部分預應力RPC 梁的配筋設計.試件設計參數見表1，表中試件編號S5-C45-P100 的意義為：S5 表示剪跨比為5.65、C45 表示張拉控制應力為0.45ffp、P100 表示預應力度為1.0，其余試件編號的意義類同.

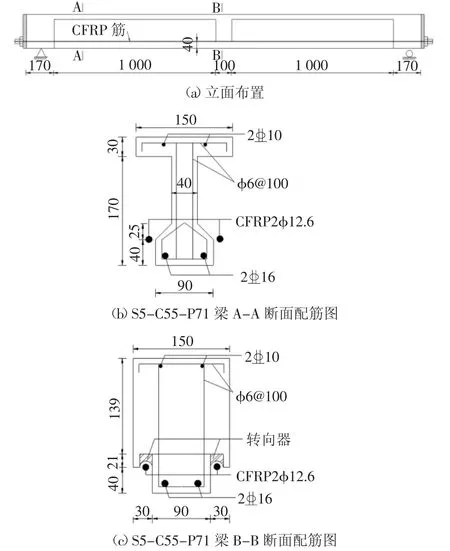
圖1 試件尺寸及配筋（S5-C55-P71）（單位：mm）Fig.1 The elevation and reinforcement of beams（S5-C55-P71）（units：mm）

表1 試件設計參數Tab.1 The design parameters of the specimens

1.2 材料性能

RPC 設計強度等級為150 MPa，質量配合比為：m水泥∶m水∶m硅灰∶m石英粉∶m石英砂∶m減水劑=1 ∶0.2 ∶0.25 ∶0.3 ∶1.1 ∶2.5，水膠比為0.16；鋼纖維為鍍銅光面平直鋼纖維，體積摻量為2%.試件自然養護48 h后再蒸氣養護72 h.采用邊長100 mm 的立方體測試強度等級；采用100 mm×100 mm×300 mm 試塊測試彈性模量和軸心抗壓強度，采用100 mm×100 mm×400 mm 試塊測試抗折強度.實測RPC 力學性能參數見表2.

表2 試件RPC 力學性能Tab.2 Mechanical properties of RPC

體外預應力筋采用圖2 所示7 絲CFRP 絞線筋，其內單絲公稱直徑為4.18 mm，有效直徑為3.72 mm，有效面積為10.9 mm2；整束絞線的公稱直徑為12.54 mm.體外CFRP 預應力筋兩端采用RPC 作為黏結介質的黏接式錨具予以錨固，實測CFRP 筋及鋼筋性能參數見表3.

圖2 CFRP 絞線筋（單位：mm）Fig.2 Configuration of CFRP strand（units：mm）

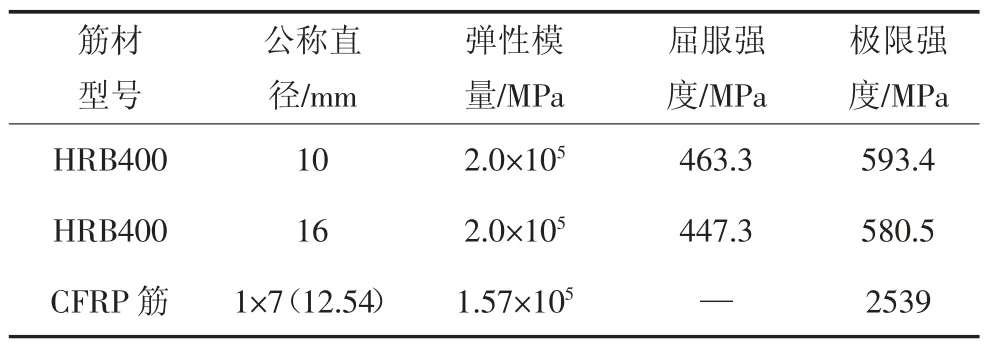
表3 CFRP 筋及鋼筋力學性能Tab.3 Mechanical properties of CFRP strand and reinforcement

1.3 預應力張拉及測試

預應力筋張拉采用圖3 所示裝置，通過2 個千斤頂單端同步施加，由錨固端穿心式壓力傳感器測量張拉力.張拉過程中用位移計測量梁的反拱值，由粘貼于混凝土表面的應變片測量跨中截面上、下緣縱向應變，并根據實測彈性模量得到相應應力，實測結果見表4，表中應力和應變記受拉為“+”，受壓為“-”.

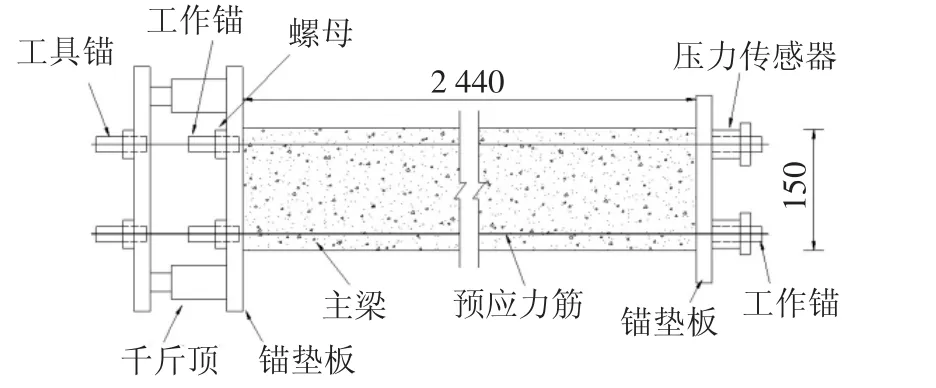
圖3 預應力張拉裝置Fig.3 Schema of prestressing set-up

表4 預應力張拉試驗結果Tab.4 Results of prestressing set-up

1.4 加載裝置及測點布置

梁S2-C45-P100 采用圖4（a）所示跨內兩點對稱加載，其余3 根梁采用圖4（b）所示跨中單點加載，均為單調加載.采用液壓千斤頂分級控制加載，由布置于千斤頂上的壓力傳感器控制加載速率和荷載大小.當加載至荷載降為峰值荷載的80%或受壓區混凝土壓碎時認為試件破壞，主動卸載.主要測試內容有：梁豎向變形、跨中截面混凝土應變、裂縫分布及發展、體外預應力增量、試件破壞形態等.加載裝置及測點布置如圖4 所示，其中a 為剪跨段長度，兩點加載時a 值為510 mm，跨中單點加載時a值為1 130 mm.

2 試驗結果分析

2.1 受力破壞過程

試驗梁主要測試結果及跨中截面荷載/彎矩-撓度曲線分別如表5 和圖5 所示.梁破壞時控制截面的形態如圖6 所示.

表5 試驗結果Tab.5 Tested results of beams

從中可見：對于3 根體內未配任何普通鋼筋的全預應力梁，其受力破壞過程相近.以梁S2-C45-P100 為例，當荷載施加到91.2 kN 時，跨中轉向塊邊緣截面受拉下緣應變達到RPC 基體初裂應變后基體開裂（圖5 荷載位移曲線中的A 點），裂縫處的鋼纖維隨即發揮其橋接作用并對裂縫發展有所抑制.當裂縫寬度發展至0.5 mm 左右時，伴隨著受拉區鋼纖維拔出的聲響，受拉邊緣鋼纖維作用逐漸消失，荷載達到峰值118.2 kN（圖5 荷載位移曲線中的B點），較初始開裂荷載增加29.6%，反映了鋼纖維的抗拉作用.此后裂縫寬度和跨中撓度發展速度加快，而荷載基本保持不變，過程中梁的受力近似于帶拉桿的扁拱[18]，直至梁體斷裂破壞（圖5 荷載位移曲線中的C 點），荷載降為0.梁S5-C45-P100 與梁S5-C55-P100 也表現出相近的破壞模式，但因梁S5-C55-P100 的有效預應力較梁S5-C45-P100 增大32.8%，使得其開裂彎矩、極限彎矩和極限撓度分別比梁S5-C45-P100 增大26.3%、30.8%和16.9%.全預應力梁均表現出類似少筋梁的破壞特征，開裂荷載由有效預應力和RPC 的基體抗拉強度決定，承載能力則由有效預應力和RPC 的極限抗拉強度所控制.3 根全預應力梁S5-C45-P100、S2-C45-P100 及S5-C55-P100 均是沿主裂縫發生梁體斷裂破壞（如圖6（a）所示），破壞時梁跨中截面頂緣實測壓應變分別為2 519 με、1 832 με 和3 313 με，均未達到RPC的極限壓應變（約為4 500 με[13]）.

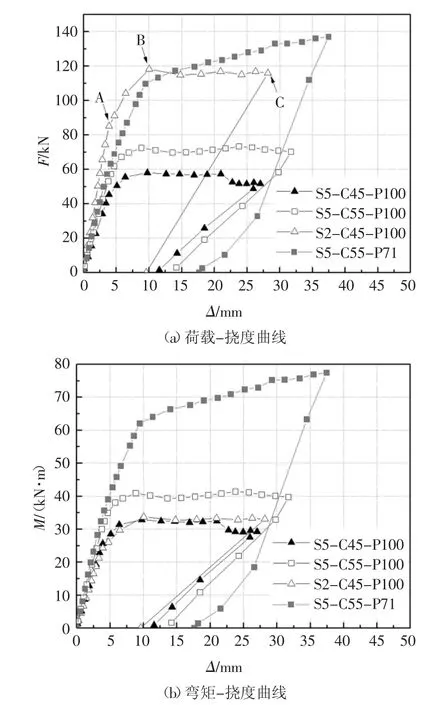
圖5 梁跨中受力-變形曲線Fig.5 Force-deformation curves for beams

體內外混合配筋的部分預應力梁S5-C55-P71，其受力過程經歷了RPC 開裂、體內受拉鋼筋屈服和受壓邊緣RPC 壓碎（如圖6（b）所示），荷載/彎矩-撓度曲線近似呈三折線，表現出延性破壞特征，破壞時跨中截面頂緣壓應變達到4 825 με.由于體內鋼筋的抗拉作用遠較RPC 中的鋼纖維強，使得基體開裂后的截面剛度降低不太明顯，并掩蓋了鋼纖維抗拉作用退出后的反應.與全預應力梁S5-C55-P100 相比，部分預應力梁S5-C55-P71 的極限彎矩和極限撓度分別提高88.7%和18.1%.可見，梁內非預應力普通鋼筋的配置可明顯提高體外CFRP 預應力RPC 梁的承載能力及變形能力，并獲得期望的破壞模式.

圖6 試件破壞形態Fig.6 Failure patterns of beams

2.2 裂縫形態

圖7 所示為試驗梁破壞時的裂縫分布，圖中粗實線為破壞時主裂縫.可見：體外CFRP 全預應力RPC 梁的裂縫分布與體外全預應力普通混凝土梁相似，只產生一條或少數幾條裂縫[18]，亦即此時RPC 中的鋼纖維并未對梁的裂縫分布產生明顯影響.全預應力梁S5-C45-P100 與S5-C55-P100 的裂縫均集中在跨中加載點附近，亦即有效預應力的改變對全預應力梁的裂縫分布無明顯影響；當采用跨中2 點加載時，全預應力梁S2-C45-P100 的純彎段內增加了數條裂縫，平均裂縫間距為179 mm，主裂縫的位置亦由跨中向加載點方向靠近，但在彎剪區內未見腹板斜裂縫產生，主要是因為梁的極限荷載較低，在彎剪和預應力共同作用下，剪壓區腹板的主拉應力仍未超過RPC 的初裂強度.相比于全預應力梁S5-C55-P100，部分預應力梁S5-C55-P71 的裂縫數目明顯增多，分布范圍更大，平均裂縫間距為124 mm.圖8 所示為最大裂縫寬度隨荷載的變化.對于全預應力RPC 梁S2-C45-P100、S5-C45-P100 和S5-C55-P100，基體開裂至峰值荷載前，裂縫寬度ω 隨荷載增長變化較小，峰值荷載點處的裂縫寬度分別為0.50 mm、0.50 mm 和0.45 mm；峰值荷載后，受拉區鋼纖維的作用逐漸消失，裂縫寬度與高度隨荷載增加快速發展，破壞時的最大裂縫寬度分別為8.4 mm、9.2 mm 和8.8 mm.對于部分預應力梁S5-C55-P71，在非預應力鋼筋屈服前，裂縫寬度發展較慢，非預應力筋屈服時最大裂縫寬度僅為0.26 mm，而此時荷載已達極限荷載的80.1%；非預應力筋屈服后裂縫寬度發展加快，破壞時的最大裂縫寬度達6.8 mm.可見，體內未布置任何普通鋼筋的全預應力RPC梁，其裂縫分布集中，且裂縫寬度發展快，與文獻[18]中給出的梁內未配置普通鋼筋的體外預應力普通混凝土梁情形類似.因此，RPC 中鋼纖維的摻入對全預應力梁裂縫分布的改善及裂縫開展的抑制作用有限，而體內非預應力筋的相應作用明顯.

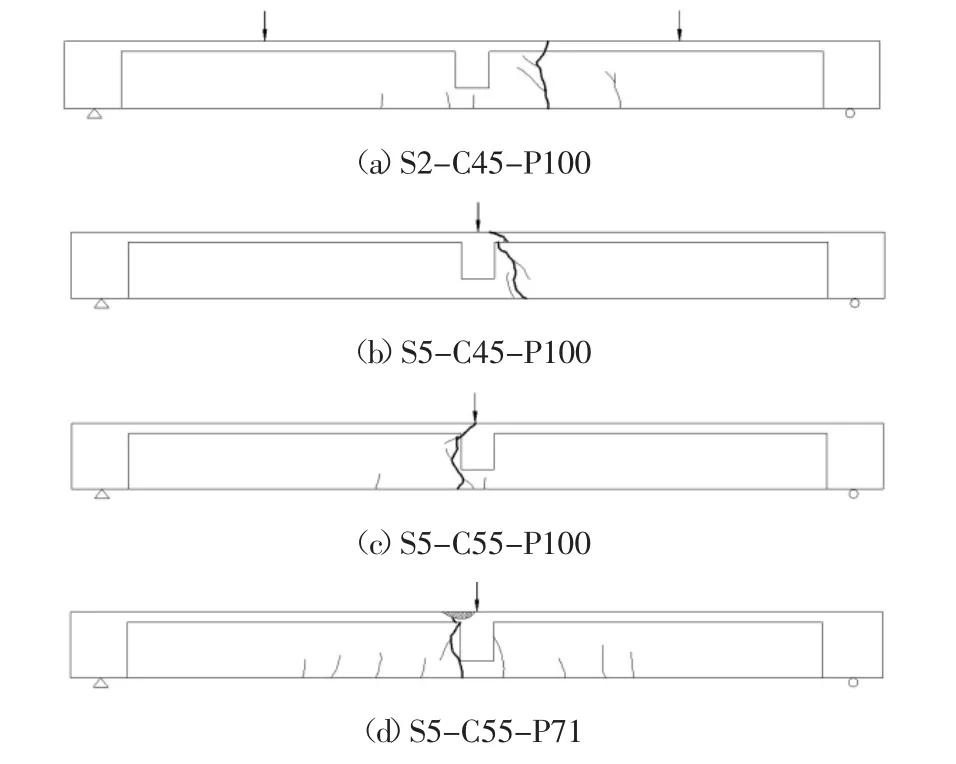
圖7 試驗梁裂縫分布Fig.7 Crack distribution of beams

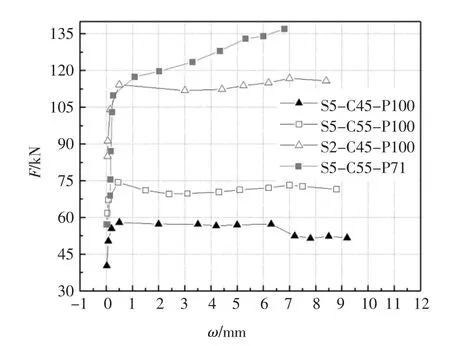
圖8 裂縫寬度隨荷載變化規律Fig.8 Load-crack width relationship of beams

2.3 體外預應力增量

圖9 所示為體外CFRP 預應力增量隨撓度的變化規律，應力增量以有效預應力為基點.可見：加載前期由于預應力施加引起梁體反拱，CFRP 預應力筋與跨中轉向器未接觸，致使體外預應力增量隨跨中撓度變化較小.當加載至梁跨中撓度接近預應力施加過程中所產生的反拱時，CFRP 預應力筋與轉向器開始接觸，體外預應力增量與跨中撓度接近線性關系，這與普通無黏結預應力配筋混凝土結構中預應力筋應力變化情況類似.

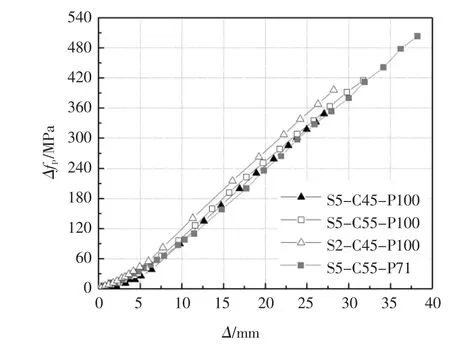
圖9 體外預應力增量-跨中撓度曲線Fig.9 External prestress increment-deflection curves

全預應力梁S5-C45-P100、S2-C45-P100 和S5-C55-P100 極限狀態時體外預應力筋的應力增量分別為348.6 MPa、396.2 MPa 和415.3 MPa，相應的極限應力分別為1 371.6 MPa、1 429.1 MPa 和1773.9 MPa；部分預應力梁S5-C55-P71 因破壞時的撓度更大，極限狀態時的應力增量達503.3 MPa，較梁S5-C55-P100 增大21.2%.非預應力鋼筋在改善體外預應力梁變形能力的同時，可提高體外CFRP 筋的極限應力增量，發揮CFRP 筋的高強特性.

2.4 延性分析

CFRP 筋為線彈性材料，CFRP 配筋混凝土結構中反映結構延性的塑性殘余變形比普通鋼筋配筋混凝土結構要小得多[13]，傳統普通配筋混凝土結構的延性指標對體外CFRP 預應力RPC 梁已不再適用.因此，這里采用基于能量的延性指標定義并有[19]：

式中：Etol=Eel+Epl為總能量，Eel為彈性能量，Epl表示塑性能量，其值可根據圖10 所示荷載（P）-撓度（Δ）關系曲線下的面積確定.

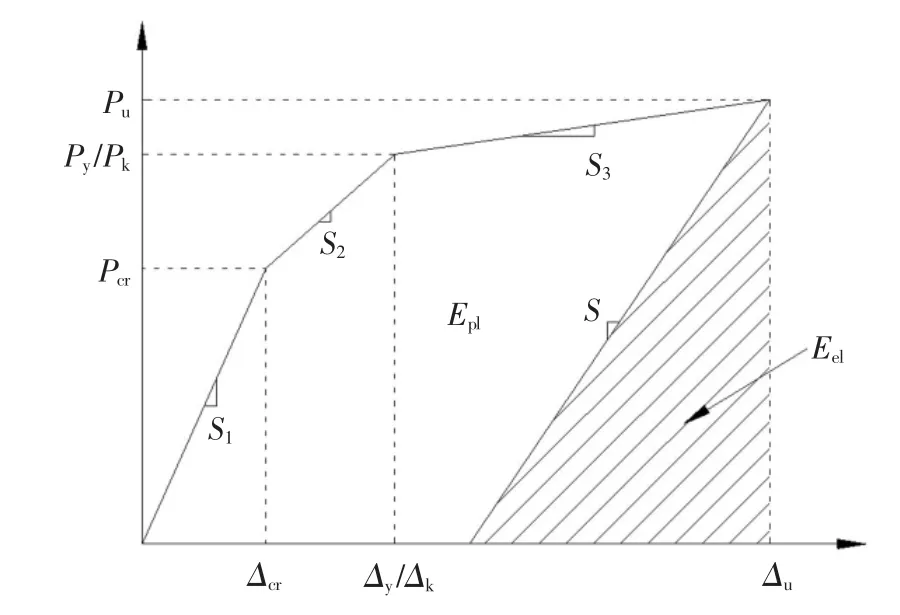
圖10 荷載-撓度曲線及相應的彈、塑性能Fig.10 Load-deflection curve and energy components

根據式（1），梁S5-C45-P100、S2-C45-P100、S5-C55-P100 和S5-C55-P71 的延性指標分別為1.973、2.007、2.094、2.568.可見，3 根全預應力梁的延性指標相近，而部分預應力梁的延性指標較全預應力梁提高約28.4%.這是因為全預應力梁的延性完全取決于RPC 的受壓塑性，而部分預應力梁的延性主要由受拉區普通鋼筋的塑性提供.

綜上，對于體外配置CFRP 預應力筋RPC 梁，RPC 中鋼纖維的摻入對全預應力梁正截面的抗彎性能改善作用極為有限，而體內非預應力筋的相應作用明顯，因此不宜過高估計鋼纖維的作用而取消體內非預應力鋼筋的配置.

3 抗彎性能分析

3.1 基本假定

分析過程中采用如下基本假定：

1）結構在變形后，截面應變符合平截面假定（體外預應力筋應變除外）.

2）體外CFRP 預應力筋在轉向器處可以自由滑動，忽略摩擦產生的影響.

3）CFRP 筋為理想的線彈性材料，鋼筋為理想的彈塑性材料；RPC 的本構關系如圖11 所示，相應的本構方程分別見式（2）和（3）[13，20].

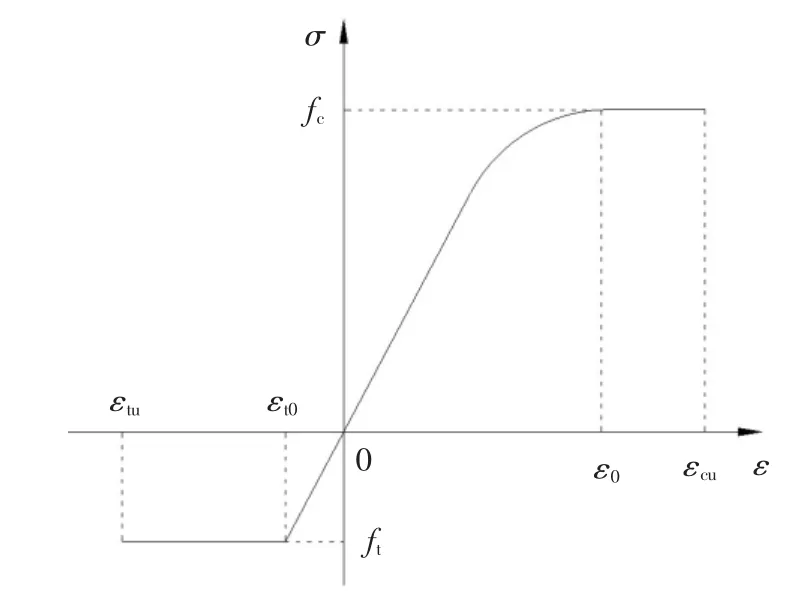
圖11 RPC 本構模型Fig.11 The constitutive relationship of RPC

RPC 單軸受壓本構方程：

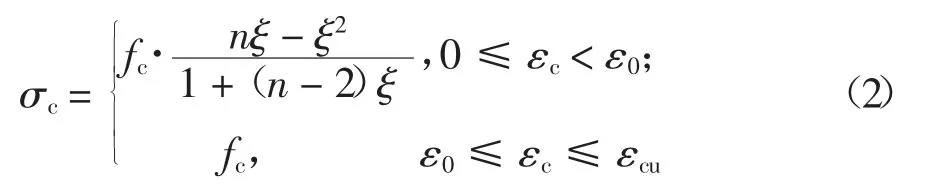
RPC 單軸受拉本構方程：

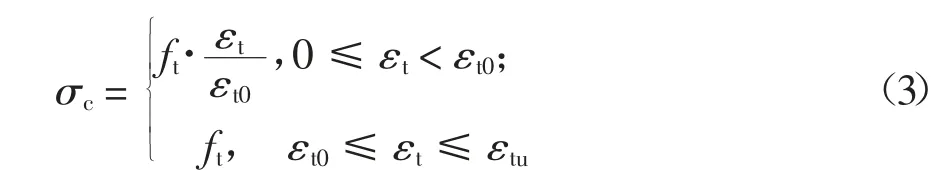
式中：fc為RPC 軸心抗壓強度；n=Ec/Es，Ec為初始彈性模量，Es為峰值點割線彈性模量；ξ=εc/ε0，ε0=3 500×10-6，εcu=4 500×10-6，ft為RPC 軸心抗拉初裂強度，ft=0.668 fr0[21]；εt0=ft/Ec；εtu=30 ft/Ec[20].

3.2 體外預應力增量計算

試驗梁在跨中設置一個轉向器，CFRP 筋與跨中轉向器接觸點豎向變形協調.將試驗梁簡化為圖12 所示的計算模型，由幾何關系可求解體外預應力增量.

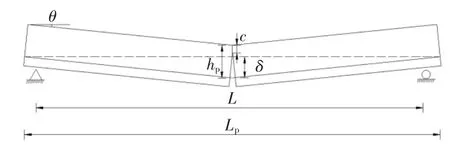
圖12 計算模型Fig.12 Calculated model

如圖12 所示，由于梁端截面轉角很小，且變形主要集中在跨中附近梁段，可據式（4）、式（5）分別近似計算梁端轉角θ 和體外預應力筋伸長量Δp：

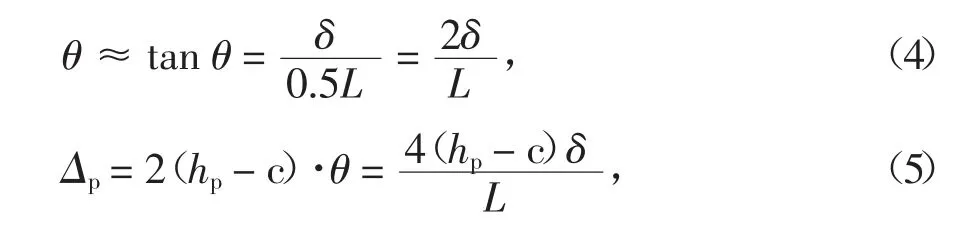
則體外預應力增量為：

式中：hp為跨中截面體外預應力筋有效高度；c 為跨中截面受壓區高度；δ 為跨中截面撓度；Ep和Lp分別為體外預應力筋的彈性模量和錨固點間長度.

3.3 開裂彎矩

考慮開裂時RPC 的受拉塑性，為簡化計算，假定開裂時受拉區應力分布為圖13（d）所示梯形分布，并取此時RPC 的受拉彈性模量為RPC 初始受拉彈性模量Et的1/2，且假定Et=Ec[22].

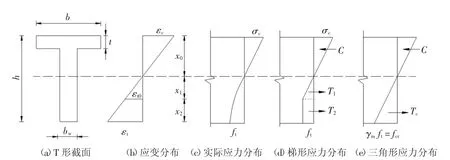
圖13 開裂時截面應變及應力分布Fig.13 Sectional strain and stress under initial cracking moment

根據靜力平衡條件可得：

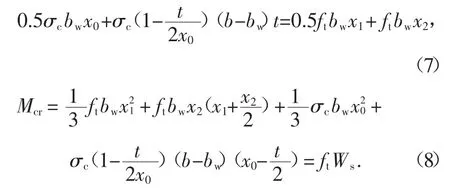
式中：bw為腹板寬；b 為翼緣寬；t 為翼緣厚度；x0為截面受壓區高度；x1為截面受拉區應變εt0點距中性軸的距離；x2為截面受拉區應變εt0點距受拉邊緣的距離；Mcr為截面開裂彎矩；Ws為換算截面對受拉區邊緣的彈塑性抵抗矩.

在保持開裂彎矩不變的條件下，將截面受拉區的彈塑性曲線應力分布（如圖13（c）所示）簡化為直線應力分布（如圖13（e）所示），則基于彈性應力分布的RPC 梁開裂彎矩可按式（9）計算.

聯立式（8）和（9），可得T 形截面RPC 梁受拉區混凝土的塑性影響系數：

式中：W0為換算截面對受拉區邊緣的彈性抵抗矩；γm為T 形截面抵抗矩塑性影響系數，根據本文試驗梁截面尺寸，可得γm=1.50.

梁體開裂時變形較小，此時體外預應力筋的應力增量亦較小可忽略，則開裂彎矩可由式（11）求得.

式中：σpc為有效預應力引起的梁底截面壓應力.

3.4 極限彎矩

3.4.1 全預應力RPC 梁

對于全預應力RPC 梁，當截面受拉邊緣應力達到RPC 的極限抗拉強度時，梁達到其承載能力.此時可采用RPC 的抗折強度fru代替式（11）中考慮受拉塑性后RPC 的初裂抗拉強度γmft，即可得全預應力RPC 梁的抗彎承載能力如式（12）.

3.4.2 部分預應力RPC 梁

極限狀態時，部分預應力RPC 梁體內普通鋼筋屈服、受壓邊緣混凝土壓碎，梁內形成塑性鉸，梁的變形主要集中在塑性鉸附近，假定梁的曲率均勻分布在塑性鉸長度（2Zp）內，則極限狀態下的塑性鉸區長度（2Zp）、曲率φu和跨中撓度δu可按式（13）計算[23].

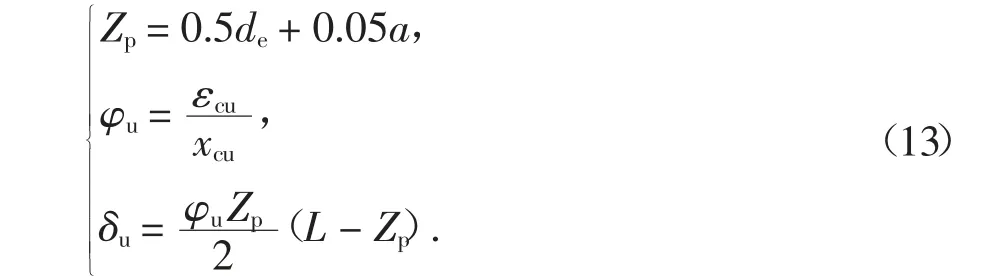
結合式（6）和式（13），可得極限狀態時CFRP 預應力筋的應力增量Δfpu：

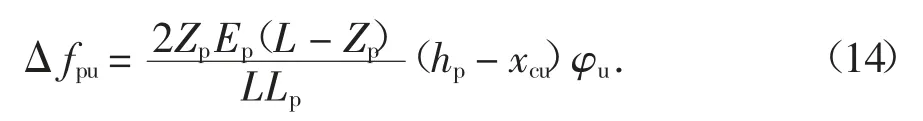
式中：Zp為塑性鉸區長度的一半；a 為剪跨長度；de為體內非預應力筋有效高度；xcu為極限狀態下跨中截面受壓區高度.

極限狀態時梁截面的應變及應力分布如圖14（b）（c）所示.考慮受拉區RPC 對結構抗彎承載能力的貢獻，為簡化計算，將受拉區及受壓區的應力分布等效為矩形應力分布，如圖14（d）所示，其中α、β 為受壓區等效矩形應力圖系數，根據RPC 受壓應力-應變關系，基于合力大小及作用點位置不變原則，可得α=0.92，β=0.74；κ 為受拉區等效矩形應力圖系數，取κ=0.25[11].

由截面內力平衡條件可得:

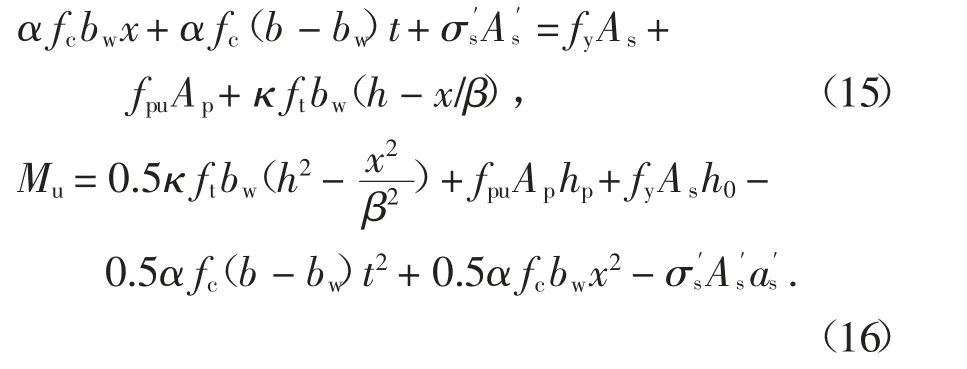
式中：Mu為截面的極限彎矩值；x 為等效矩形受壓區高度；fpu為極限狀態下預應力筋應力，fpu=fpe+Δfpu，可根據式（14）求得.

試驗梁開裂彎矩及極限彎矩計算值與試驗值的比較見表6，可見，二者吻合較好，驗證了上述公式的適用性.

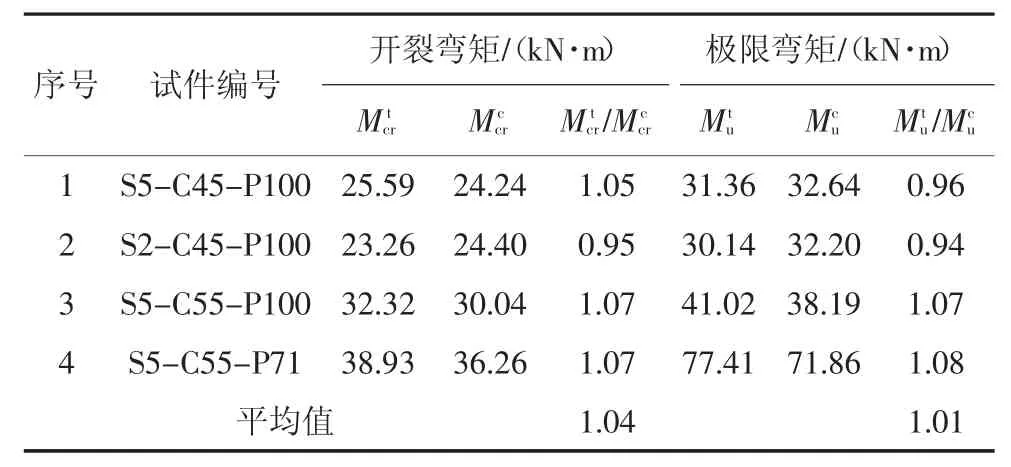
表6 試驗結果與計算結果比較Tab.6 Comparison of test and predicted results

4 結論

1）體外CFRP 預應力筋全預應力RPC 梁均發生“少筋”特征的脆性斷裂破壞.RPC 中鋼纖維的摻入，雖然可使全預應力梁在RPC 基體開裂后的承載能力和變形略有增加，但并不能改變全預應力梁的脆性破壞特征，因此鋼纖維的摻入不能完全替代普通鋼筋的作用.

2）體外CFRP 預應力筋部分預應力梁，梁內非預應力普通鋼筋的配置可明顯提高梁的承載能力及變形能力并獲得期望的延性破壞模式.RPC 中鋼纖維的摻入對全預應力梁正截面的抗彎性能改善作用極為有限，而體內非預應力筋的相應作用明顯.因此，對于實際工程中的體外預應力RPC 梁，不宜過高估計鋼纖維的作用而取消體內非預應力鋼筋的配置.

3）推導了體外CFRP 預應力RPC 梁開裂彎矩和極限彎矩計算公式并以試驗結果驗證了其適用性.