基于信息熵與遺傳算法的并行關聯規則增量挖掘算法

毛伊敏，鄧千虎，陳志剛

（1.江西理工大學信息工程學院，江西 贛州 341000；2.中南大學計算機學院，湖南 長沙 410083）

1 引言

關聯規則是數據挖掘的一個主要研究領域，其目的在于發現數據集中有價值的潛在頻繁模式[1]。目前，關聯規則挖掘已被廣泛應用于購物推薦、網站點擊分析、電子商務、金融和醫療診斷等領域，產生了極大的社會與經濟效益[2-3]。靜態關聯規則挖掘是在固定的數據集以及支持度閾值下，對數據集中的頻繁模式進行挖掘，如Apriori[4]、FP-Growth[5]、Eclat[6]等。但這些靜態關聯規則算法并未考慮到數據庫中的事務發生變化或是關鍵的支持度閾值發生變化的增量挖掘工作，這將導致算法需對整個數據集進行重復處理，造成大量的時空間消耗。針對此問題，Leung 等[7]提出了一種基于 CATS（compressed and arranged transaction sequences）樹改進的Can 樹（Canonical order tree）來簡化增量挖掘工作，極大地提高了算法的運行效率。但在大數據環境下，隨著數據量的指數級增長，運算時間過長和內存占用過高已成為傳統關聯規則算法處理海量數據的重要瓶頸[8]。因此，提高算法的并行化效率使之能高效地對海量數據進行處理是目前迫切需要解決的問題。

MapReduce 是Google 公司為解決海量數據處理提出的一種分布式并行運算框架[9]，具有使用簡單、成本低廉、系統擴展性好以及負載均衡等優點，目前已被廣泛應用于大數據分析與處理等領域。基于此，Song 等[10]提出了一種大數據環境下的并行頻繁項集挖掘算法IncMiningPFP，結合MapReduce計算框架實現了Can 樹向并行化方向的遷移，極大地提高了基于Can 樹的增量挖掘算法的并行化運算能力。但該算法在使用Can 樹結構存儲所有數據信息以加快后續增量挖掘的同時，也會導致最終產生的樹結構極其龐大。針對此問題，胡軍等[11]使用一種基于數據量排序的Can 樹構造方法，將各事務中的數據項按出現頻次進行排序，然后根據排序后的事務進行樹結構構建，使各個事務中相同的數據項盡量共用一個樹節點，從而降低最終生成的樹結構的空間占用。但此方法在適用性與可行性方面具有較大的局限性，因此對Can 樹結構空間占用過大的問題仍然有待進一步改進。

此外，支持度閾值的設定對關聯規則算法而言也是極其關鍵的問題。大數據的數據規模更大，但數據的價值密度卻隨之下降，當設定的支持度閾值較小時，將會產生大量冗余的無效頻繁項集；當使用相對較大的支持度閾值時，則可能在減少冗余項集的同時丟失一些高質量的頻繁項信息，使最終生成的頻繁項的整體質量偏低。針對該問題，Ragaventhiran 等[12]在應用MapReduce 框架并行化挖掘Can 樹頻繁模式的同時，設計了基于多支持度的頻繁模式挖掘方法，在不同的支持度閾值下進行頻繁模式挖掘，根據挖掘結果來獲取最優的支持度閾值。但該算法僅支持特定的閾值取值范圍，并未對大數據環境下的閾值取值進行優化，難以根據相對最優的動態支持度閾值獲取最終結果。

對于基于Can 樹的并行挖掘算法，除了Can 樹結構空間占用過大以及支持度閾值難以動態設定的問題外，在MapReduce 的并行化運算中，Map與Reduce 進程之間的數據傳輸過程也會對系統的整體性能產生極為重要的影響。Map 任務在內存中產生的數據需要先存儲到磁盤，再由Reduce 進程從中讀取數據，但磁盤與內存之間I/O 速度的極大差異將會導致這一數據傳輸過程消耗大量時間等待內存區數據寫入磁盤，最終影響算法的運行速度。因此，申玲艷[13]設計了針對Map 端輸出數據的優化策略，將多個Map 任務同時產生的輸出數據進行合并，在內存區數據量達到閾值后將數據寫入磁盤，使Reduce 任務能夠獲取更加緊湊的Map 端輸出數據，從而提高數據傳輸效率，加快數據傳輸過程；Cao 等[14]提出了一種優化Map 中間輸出數據的通信方法，對MapReduce 任務中的數據通信活躍度進行量化，使用Bayes 算法進行分類預測，根據分類結果將Map 端輸出的通信活躍的數據映射到同一分區中，通過優化傳輸流程來加快Map 與Reduce 之間的數據傳輸。但這些算法都存在一定的局限性，當Map 端單個節點輸出的數據規模已經達到內存區閾值或是輸出數據的活躍度相差不明顯時，這些改進算法對整體的性能提升效果并不明顯。

綜上，盡管上述算法取得了一定成效，但如何有效降低Can 樹結構的空間占用、獲取大數據環境下相對合適的動態支持度閾值、加快Map 與Reduce階段的數據傳輸等問題仍然是目前亟待解決的。針對這些問題，本文提出一種基于信息熵和遺傳算法的并行關聯規則增量挖掘算法MR-PARIMIEG。本文主要貢獻如下。

1) 設計基于信息熵的SIM-IE 策略來合并數據集中的相似數據項，根據合并后的數據集進行Can樹構造，降低了最終生成的Can 樹結構的空間占用。

2) 提出基于遺傳算法的DST-GA 策略，以獲取大數據集中的相對最優的動態支持度閾值，根據此動態閾值進行頻繁模式挖掘，避免了冗余的頻繁模式挖掘導致的時間消耗。

3) 使用并行LZO 數據壓縮算法對Map 端輸出的數據進行壓縮來減少傳輸的數據規模，從而減少了內存與磁盤之間的I/O 操作頻次，最終加速Map與Reduce 階段的數據傳輸過程。

2 相關概念介紹

2.1 Can 樹

Can 樹是一種適用于增量挖掘的樹形數據結構，在進行增量挖掘時，其挖掘過程不受最小支持度或數據信息變化的影響，且具有較高的挖掘效率。構造Can 樹時首先將事務中所有的數據項按照某種特定順序（字典序、字母序等）進行排序，然后進行樹結構構造，在后續對增量關聯規則進行挖掘時只需要將增量數據直接更新至原有的Can 樹中[15]。給定如表1所示的數據集，Can 樹的構建過程如圖1 所示。

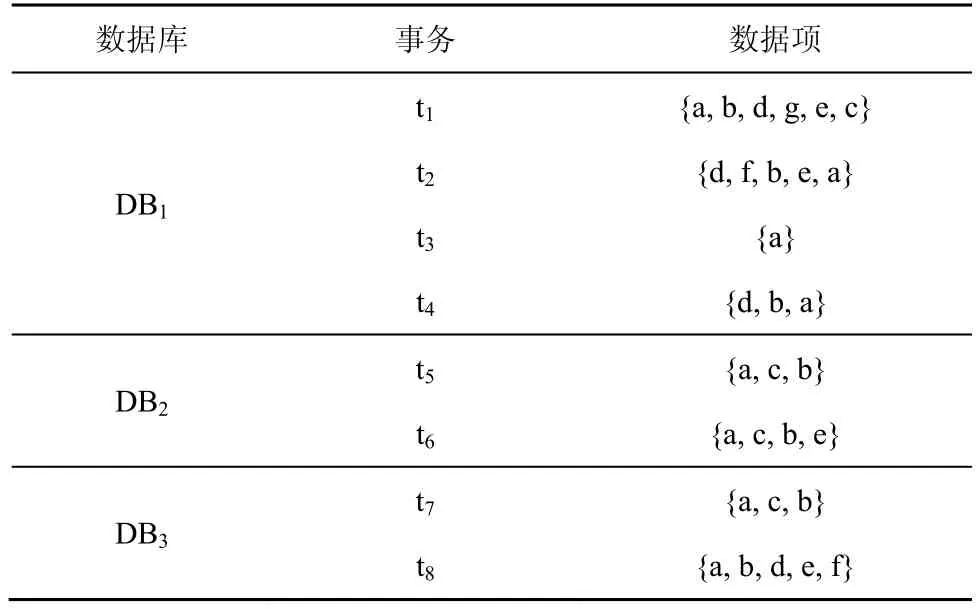
表1 數據集

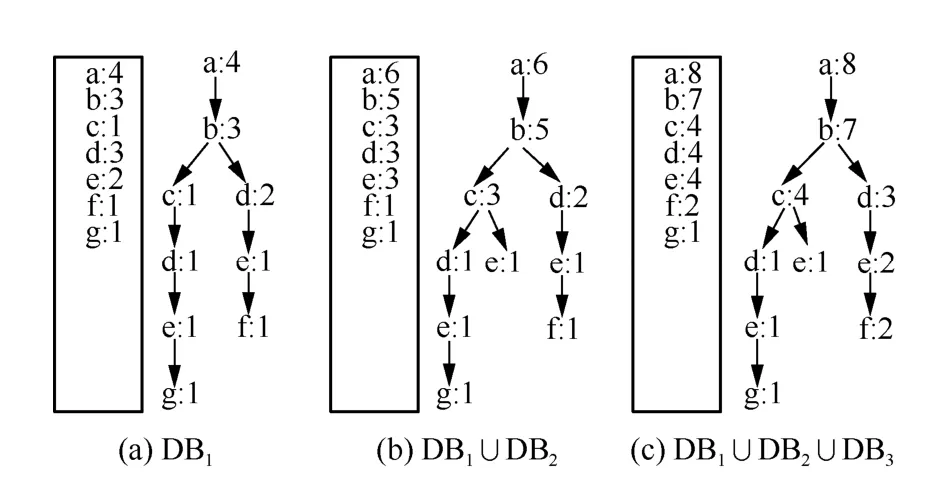
圖1 Can 樹構造過程

2.2 信息熵

信息熵是一種反映不確定性的度量方式，通過信息量的規模來體現不確定程度。在不同數據項之間的相似度判斷中，信息熵的值能相對合理地反映數據項中各屬性之間的相似性。即信息熵的數值越大，信息量的規模也相對越大，從而數據項之間的相似性越高[16]。

定義1信息熵。令x={x1,x2,…,xn}為事務集，P(xi)為對應事務的概率值，那么事務集x的信息熵H(x)可表示為[16]

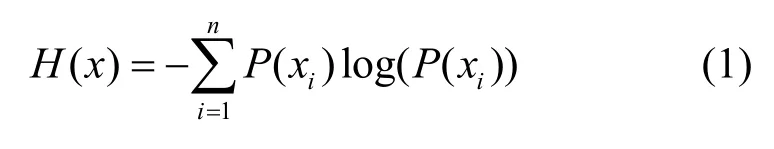
2.3 Dempster 組合規則

Dempster 組合規則是一種基于多維信息的組合規則，對具有少量沖突信息的多維信息有較高的處理效率。在對相似度較高的數據集的概率進行合并的問題中，各數據項的屬性在形式上具有較大的相似性，沖突項較少。因此該問題在形式上符合需求，可以使用Dempster 組合規則進行求解[17]。

定義2Dempster 組合規則。設A、B為2 個數據集，C為集合A、B進行數據合并后的集合，f1、f2分別是集合A、B的概率分配函數，Ω是集合A、B不相交的概率總和，φ為A、B的交集，那么A、B合并后獲得的集合C的概率P(C)為

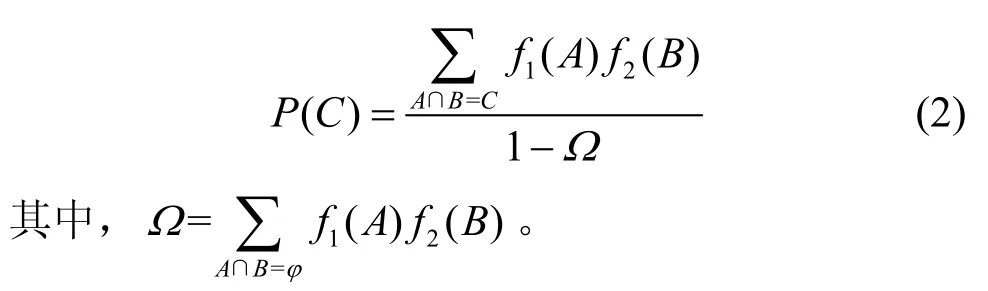
2.4 LZO 數據壓縮算法

LZO 數據壓縮算法是一種基于字典模型的無損壓縮算法，可實現對數據的高效壓縮。并行LZO數據壓縮算法針對現代計算機的多核多線程CPU結構，使用多線程技術來高效利用CPU 的運算能力，通過控制線程（control）、壓縮線程（compression）以及重構線程（reconstruction）3 種線程，實現對數據塊的并行化高效壓縮[18]。在MapReduce 分布式計算框架中，利用集群的并行運算能力來實現并行化的LZO 數據壓縮算法，從而通過壓縮數據減少傳輸的數據規模，加快Map 與Reduce 階段的數據傳輸過程。并行LZO 數據壓縮算法的具體實現流程如圖2 所示。

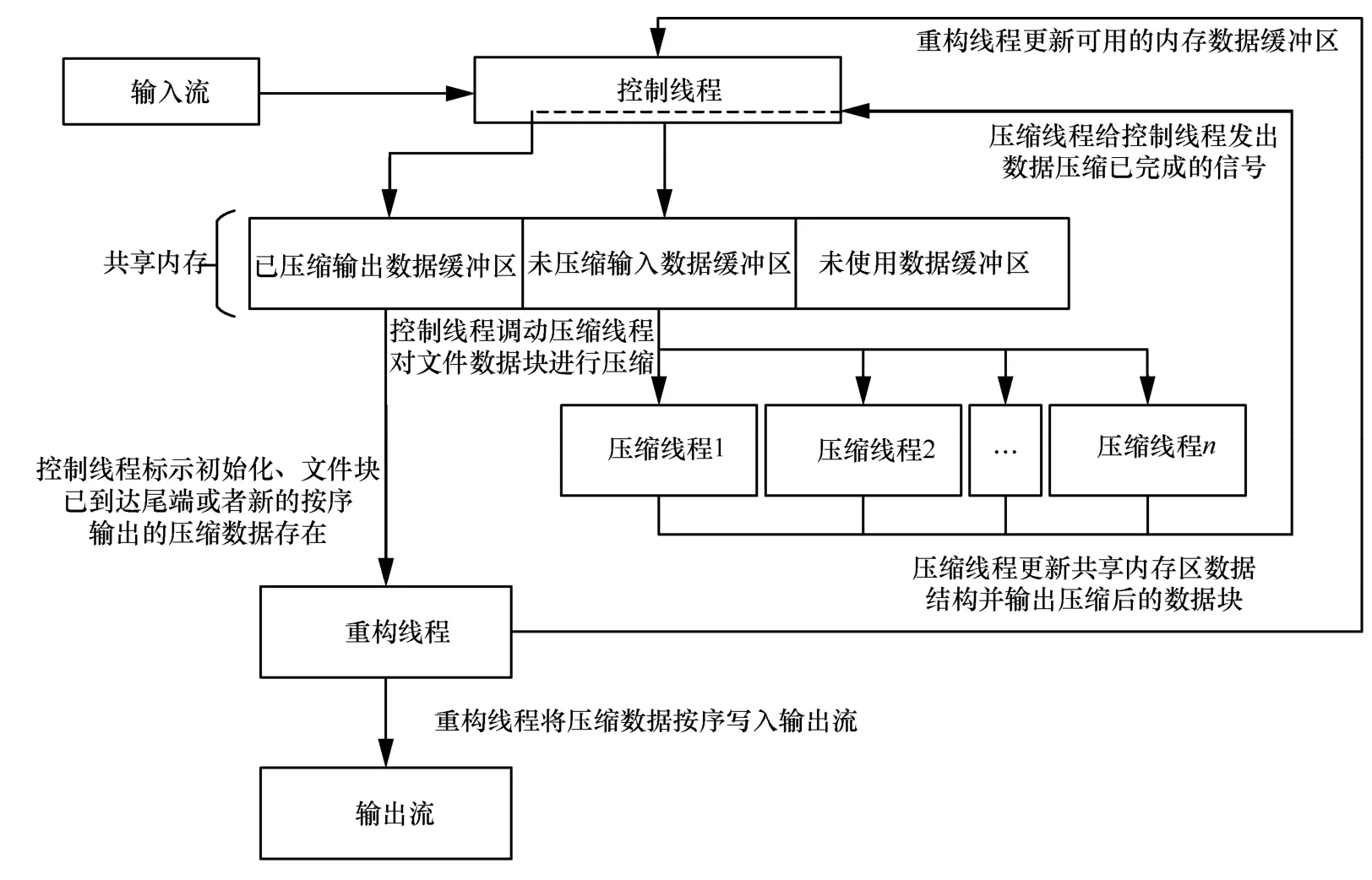
圖2 并行LZO 數據壓縮算法的具體實現流程

3 MR-PARIMIEG 算法

3.1 算法思想

MR-PARIMIEG 主要分為3 個階段，分別為相似項合并、動態支持度閾值獲取以及頻繁項集并行挖掘，各階段的主要任務如下。1) 在相似項合并階段，首先對數據集進行劃分，然后使用相似性評估公式對劃分數據集的相似性進行評估，最后根據相似度閾值合并相似項并更新全局概率值。2) 在動態支持度閾值獲取階段，根據數據集構造支持度函數，然后基于遺傳算法的求解過程構造動態閾值公式來獲取支持度函數的最優解，即動態支持度閾值。3) 在頻繁項集并行挖掘階段，將數據挖掘任務向MapReduce 平臺進行遷移，并使用并行LZO 數據壓縮算法對Map 端輸出數據進行壓縮，來加快Map 與Reduce階段的數據傳輸過程，最后在Reduce階段根據動態支持度閾值從樹結構中并行挖掘頻繁項集。

3.2 SIM-IE 策略合并相似項

基于Can 樹結構的增量關聯規則挖掘算法在構建樹結構時會存儲所有的數據項，因此在數據量較大時最終生成的樹結構將極其龐雜。基于此，本節提出SIM-IE 策略以合并數據集中的相似項，從而簡化最終生成的樹結構，降低樹結構的空間占用。SIM-IE 主要包含以下3 個步驟。1) 數據集劃分：計算數據項的平均差，并將平均差與數據項之間的差值進行比較，從而對數據集進行劃分。2) 相似度計算：根據劃分后的數據集計算信息熵和條件熵，以獲取各數據集之間的相似度。3) 相似項合并：將各數據集之間的相似度與相似度閾值進行比較，由此進行相似項合并，同時計算并更新合并后的數據集的全局概率。

3.2.1數據集劃分

對于構成Can 樹的數據項而言，對其進行排序后數據項將按值大小進行分布，那么相鄰的數據項之間的差值可以直觀地反映數據的鄰近性，即相鄰項的差值越小，那么這2 個數據項就越鄰近，因此可根據差值大小對數據項進行分類。平均差反映了整個數據集的平均鄰近距離，根據平均差將具有平均鄰近性的數據項劃分為一類，而相鄰項之間的差值大于平均鄰近距離的項則劃分到不同的數據集合中，可以將整個集合中的數據相對合理地劃分到不同的數據集中。因此，將數據項的平均差作為評價標準以進行數據劃分是較可行的一種劃分方法，這種平均的劃分方法首先將數據集進行合并與排序，然后計算各數據項之間的差值，從而求得平均差，最后根據平均差進行數據劃分。具體的劃分過程如下。

①對需要進行相似性評估的數據集中的數據項進行合并，然后按序排列，求出各相鄰數據的差值總和sum。令數據項數為n，那么求得的平均差為avg=sum/(n?1)。

②求得平均差avg 后，即可將排序后的數據集根據avg 進行劃分。設劃分數為d，如果相鄰的數據值之差小于平均差，那么就將前一個劃分獲得的數據與當前的數據之間的所有數據項歸為一個分區，重復執行比較與分區操作，直至所有數據都被劃分到對應的數據分區。

3.2.2相似度計算

獲得劃分好的數據之后，即可根據相似性評估公式計算對應的數據集之間的相似度，具體的計算過程如下：首先獲取劃分數、被劃分的不同數據集的數量以及數據集規模，然后根據相似性評估公式SAF 求得對應的條件熵以及信息熵，最終獲得數據集之間的相似度。

定理1相似性評估公式SAF。令A、B為2 個相似性待判斷的數據集，S為決策模式屬性集，C為不確定匹配模式關系集，C與S交集為空，那么可根據對應的條件熵以及信息熵求得A、B之間的相似度。

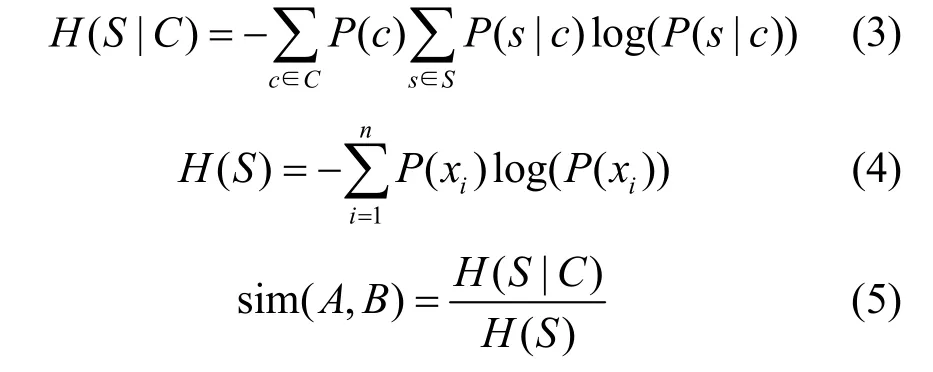
證明令O為決策模式屬性有限集，那么可求得信息熵的不確定率為μ=1 ?(H(C)+H(S|C)?H(S))/(log(O)?H(S))。設R1和R2為模式集O中的等價關系，H(S1)和H(S2)為其對應的信息熵，則有如下屬性。

①若R1=R2，那么H(S1)=H(S2)，故μ滿足不變性。

② 對于?C,S∈O，均有(H(C)+H(S|C)?H(S))/(log(O)?H(S)) ∈[0,1]，即μ∈[0,1]，故μ滿足非負性。

③若R1＞R2，那么H(S1)＞H(S2)，故μ滿足單調性。

綜上所述，SAF 中信息熵的不確定因子μ同時滿足不變性、單調性以及非負性，因此SAF 可以作為不確定數據集相似性評估的基本準則公式。

證畢。

3.2.3相似項合并

根據SAF 獲取所有劃分數據集之間的相似性結果后，再根據提前設定的相似度閾值δ判斷是否需要進行相似項合并，即將經過計算求得的相似度數值sim(A,B)與δ進行比較，若sim(A,B)≥δ，則進行相似項合并，同時對相似項合并后的全局概率值進行計算并更新。具體運行過程如下。

①獲取所有的相似項并循環合并這些項集，將所有的數據元組放入同一個數據表。

②從合并后的項集中獲取具有相同數據的元組，保留一個元組并刪除其他重復項。

③通過概率合并公式PM-DCR 對相似項的概率進行合并計算，得到刪除重復項之后的項集的全局概率值。

定理2概率合并公式PM-DCR。令p1、p2分別為項集S1、S2的全局概率，p1p2為S1、S2相交的概率，p1(1?p2)、(1?p1)p2均為S1、S2不相交的概率，S1、S2合并后的項集的概率為

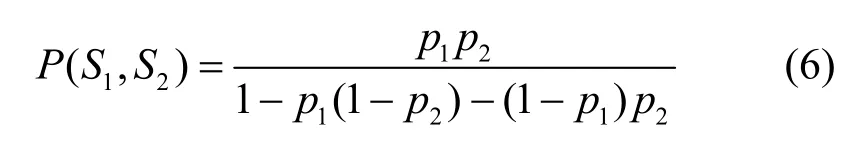
證明令H1、H2、H3為識別框架Θ的獨立證據體，m1、m2、m3分別為H1、H2、H3的信任指派函數，那么PM-DCR 有如下屬性。

①對于H1、H2，P(H1,H2)=P(H2,H1)，即m1⊕m2=m2⊕m1，故PM-DCR 滿足交換律。

② 對于H1、H2、H3，P(H1,H2,H3)=P(P(H1,H2,H3)=P(H1,P(H2,H3))，即m1⊕m2⊕m3=(m1⊕m2)⊕m3=m1⊕(m2⊕m3)，故PM-DCR 滿足結合律。

③如果m1、m2均為單調函數，使用PM-DCR對其進行融合時，有m3=m1⊕m2，那么m3也是單調的，故PM-DCR 滿足單調性。

④ 使用PM-DCR 對Θ中的證據元素進行融合后，隨著單個子集合的信任指派值增加，對應元素的信任指派值會隨之降低，故PM-DCR 滿足極化性。

綜上，PM-DCR 同時滿足交換律、結合律、單調性以及極化性，是一種可行的Dempster 組合規則改進方法，因此PM-DCR 可對相似項的概率值進行合并計算，證畢。

相似項合并過程的偽代碼如算法1 所示。

算法1相似項合并

輸入集合A、B，數據規模M、N，劃分數K，相似度閾值δ

輸出合并相似項后的數據集D

3.3 動態支持度閾值獲取

一般而言，挖掘關聯規則時的支持度閾值需預先設定好且始終保持不變，但對于大數據集來說，由于其數據價值密度降低并且數據始終處于動態變化之中的新特性，固定的支持度閾值已不足以反映其關聯規則的變化情況。為了獲取相對最優的動態支持度閾值，MR-PARIMIEG 設計了一種DST-GA 策略，實現過程如下：支持度函數構造，根據具體的數據集信息構造支持度函數；動態閾值獲取，基于遺傳算法的收斂性求取函數的最優解，即動態支持度閾值。

1) 支持度函數構造

大數據環境下，為適應數據的新特性，需要對支持度閾值做出調整以使其逐漸趨于用戶感興趣的或是有價值的關聯規則，這一動態交互過程的實現即對動態支持度閾值的求解過程。基于此，DST-GA 提出了支持度函數的定義，并將這一過程公式化為基于極值定理的最優值問題求解。

定理3支持度函數SF。令m表示數據集D的屬性數，P(xi)表示項目xi在D中出現的概率，Weight(xi)表示xi的權重，r(x1,x2,…,xm)表示修正函數，那么支持度函數SF可表示為

證明支持度函數為連續有界函數，最終的支持度閾值主要取決于各個數據項的概率值P(xi)以及對應的權重值Weight(xi)。對于，數據集的項目概率值的變化將直接反映到最終的公式化計算中。因此，當數據集信息發生變化時，SF 可以根據改變后的信息對進行計算，同時更新|D|，最終獲得適用于更新后數據集的支持度閾值。證畢。

2) 動態閾值獲取

構造支持度函數SF后，利用遺傳算法的收斂性與不失一般性，對其進行迭代優化運算以求得最優解[19]，即相對最優動態支持度閾值。具體的求解過程如下。

①根據極值定理可求得連續的支持度函數在其定義域內的極小值ξ1與極大值ξ2，所要求的動態支持度閾值必然介于ξ1、ξ2之間。

② 基于遺傳算法的收斂性，在數學問題的優化求解過程中，當循環迭代的運算次數足夠多時最終結果將會收斂于特定值。

③將遺傳算法應用于支持度函數的極值問題求解過程中，提出求解動態閾值的minSF 公式將這一迭代優化過程具象化，經過多次迭代后最終ξ1、ξ2的差值趨近于0，最終結果收斂于特定值，即相對最優動態支持度閾值。

定理4動態閾值公式minSF。令數據變量集x=(x1,x2,…,xm)T，x中任意數據項xi的取值范圍為[ai,bi]，那么根據遺傳算法求取支持度函數中動態最優值的計算式為

算法2 給出了獲取動態支持度閾值時，整體運行流程的偽代碼。

算法2動態支持度閾值獲取

輸入數據集D，各數據項對應概率數組P，GA 迭代次數N

輸出動態支持度閾值DST

3.4 頻繁項集并行挖掘

經過前述工作，已經獲得了適用于增量挖掘的動態支持度閾值以及合并相似項后的數據集。為了并行化挖掘頻繁項集，將挖掘過程向MapReduce計算平臺遷移，同時使用并行LZO 壓縮算法對Map階段輸出的數據進行壓縮，以加快Map 與Reduce階段的數據傳輸過程，最終加速算法運行。

MR-PARIMIEG 結合MapReduce 并行挖掘頻繁項集的過程分為初始挖掘與增量挖掘2 個部分，2 個過程的主要區別在于增量挖掘時需要根據新增數據集的事務項對初始挖掘階段構造的Can 樹進行更新，然后從更新的樹結構中挖掘頻繁項集。MR-PARIMIEG 算法并行挖掘頻繁項集的具體過程如下所示，并在圖3 中給出了總體的運行過程。

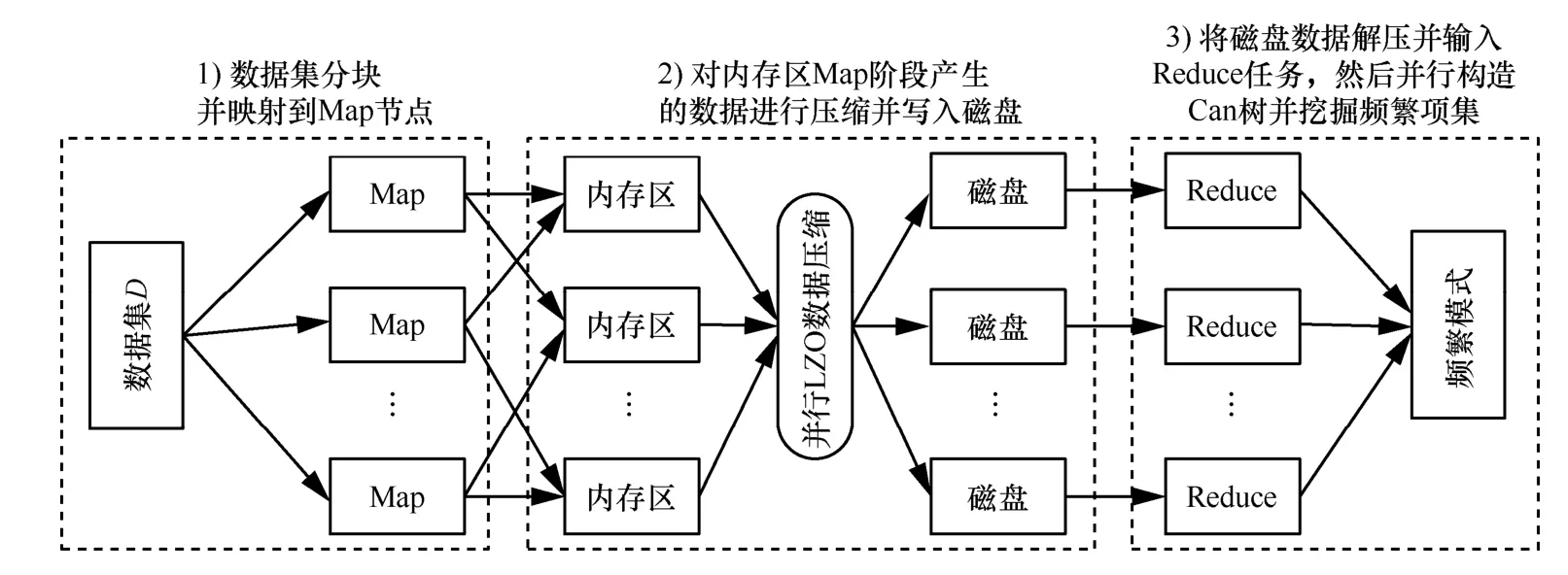
圖3 頻繁項集并行挖掘過程

1) Map 階段。掃描合并相似項后的原始數據集或新增數據集的所有數據項，并根據具體的集群節點配置情況對數據進行分塊，最后將劃分好的數據塊映射到每個計算節點進行Map 運算。

2) 數據壓縮階段。將Map 階段的輸出數據使用并行LZO 數據壓縮算法進行壓縮，具體的數據壓縮過程如下。①掃描MapReduce 集群，以獲取處于空閑狀態的計算節點，基于負載均衡策略將Map端輸出的數據分配給所有可用節點進行處理。②在內存中創建3 種線程，分別是控制線程、壓縮線程以及重構線程，使用信號量保護的共享內存進行3 種線程間的信號交流。③將數據分塊并輸入內存，通過主控線程控制數據流向并初始化壓縮線程，將所有的壓縮線程相對均衡地分布到可用的處理器核心中，然后使用壓縮線程各自獨立地對數據塊進行并行壓縮。④使用重構線程獲取各個壓縮線程中生成的壓縮數據塊，并按輸入順序輸出所有的壓縮數據，最后在壓縮數據輸出到磁盤后進行解壓供Reduce 任務調用。

3) Reduce 階段。在初始挖掘時，根據Map 階段的輸出數據并行構造Can 樹，并使用Hash 表記錄所有數據項在樹結構中的相對位置以加快數據查找速度，最后根據動態支持度閾值從樹結構中挖掘頻繁項集；在增量挖掘時，根據Map 階段的輸出數據對Can 樹以及存儲數據項位置信息的Hash 表進行更新，根據更新后的Can 樹和動態支持度閾值并行挖掘頻繁項集。

頻繁項集并行挖掘的執行過程偽代碼如算法3所示。

算法3頻繁項集并行挖掘

輸入數據集D，支持度閾值ST

輸出頻繁N項集

3.5 算法分析

對于本文提出的MR-PARIMIEG 算法，其時間復雜度主要由相似項合并、動態支持度閾值獲取以及頻繁項集并行挖掘3 個部分構成，這些階段的時間復雜度如下所示。

1) 進行相似項合并時需要掃描數據集中的每個數據項并對數據集進行劃分，然后計算相似度。令總數據項數為n，劃分數為d，那么時間復雜度為T1=O(d2+n2)。

2) 獲取動態支持度閾值時，根據遺傳算法的遺傳迭代獲取最優解思想，令迭代次數為M，其中每次迭代進行遺傳演化時均需要對整個數據集進行處理，那么該階段的時間復雜度為T2=O(nM)。

3) 關聯規則并行挖掘階段需要多個運算節點對數據進行壓縮以加快內存與磁盤的數據交換過程，然后并行構建或更新Can 樹結構并從中獲取頻繁項集。令MapReduce 分布式集群的節點數為r，那么其時間復雜度為T3=O(rlogn)。

因此，對于MR-PARIMIEG，其總的時間復雜度為T=O(d2+n2+nM+rlogn)，其中r＜＜n、M＜＜n,所以最終的時間復雜度近似為T=O(d2+n2)。

對于FPM-HCG 算法[8]，在數據準備階段，由于其采用了滑動窗口技術來對數據進行掃描，然后將數據更新至Can 樹結構中，同時需要維持一個映射Can 樹進行頻繁項挖掘的GTree，令滑動窗口大小為k，那么該階段的時間復雜度為O(kn2)；在頻繁項集并行挖掘階段，由于未對磁盤與內存之間的數據傳輸過程進行優化，因此在集群節點數為r時，該階段的時間復雜度為O(rn)。因此，FPM-HCG 的時間復雜度近似為O(kn2)。

對于IncbuildingPFP[10]算法，需要對數據進行2 次掃描以獲取所有的數據信息，該階段的時間復雜度為O(n2log(n))；在對頻繁項進行并行挖掘時，其時間復雜度與FPM-HCG 基本相同。因此，IncbuildingPFP 的時間復雜度近似為O(n2log(n))。

對于MR-PARIMIEG，由于d為對數據集進行劃分的劃分數，因此d＜n，故其時間復雜度O(d2+n2)＜O(2n2)；對于FPM-HCG，k為滑動窗口大小，決定了每次對數據庫進行掃描能保存的數據量，其數值小于log(n)但大于 2。由于O(d2+n2)＜O(2n2)＜O(kn2)＜O(n2log(n))，故相較于FPM-HCG 算法和 IncbuildingPFP 算法，MR-PARIMIEG 算法具有更理想的時間復雜度。

4 實驗與分析

4.1 實驗環境

本節對本文提出的MR-PARIMIEG算法設計了一系列實驗來驗證其性能。具體的實驗硬件配置為主從結構的分布式集群，其中包含一個主節點和4 個從節點。所有節點的硬件配置均為 Intel core i9-9900K 八核處理器、16 GB 內存、1 TB 固態硬盤，各節點通過500 Mbit/s 的網絡進行連接，且均處于同一局域網中；軟件配置則統一安裝Ubuntu16 操作系統、jdk1.8 版本的Java 環境以及Hadoop2.7.5分布式計算平臺。

4.2 實驗數據

本文中實驗所用數據為4 個真實的數據集，分別是RetailRocket、Accident、Susy 和Jester[20]。RetailRocket 是一個記錄電子商務網站用戶行為的數據集，記錄了時間跨度為4～5 個月的網站訪問者的操作數據，操作分為商品點擊瀏覽、加入購物車和購買等，總計有2 756 101 個操作事件，數據量較多且較離散；Accident 是一個交通事故數據集，包含340 183 條數據，數據量較少，數據分布相對均勻；Susy 是記錄粒子探測數據的數據集，數據項數為28，總的數據記錄數為500 萬，數據項數少且數據長度相對均勻；Jester 是一個評分數據集，記錄了73 421 個用戶對100 個笑話給出的410 萬個評分數據，數據連續性強且取值區間較小。這些數據集的詳細信息如表2 所示。

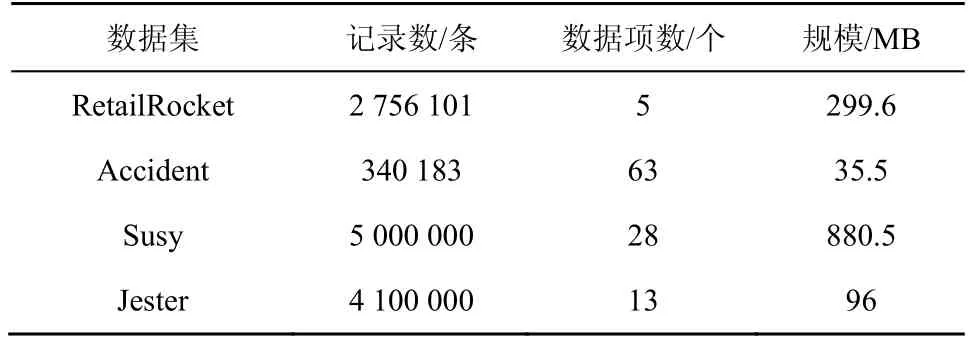
表2 數據集的詳細信息

4.3 評價指標

1) 加速比

為了確定并行化算法對數據進行并行處理的效率，可以使用加速比作為評價指標以衡量算法的并行化運算能力。加速比是通過并行計算以降低總體的運行時間而獲得的性能提升的數值化表示形式，其定義為

其中，T1表示算法在單節點中的運行時間；Tn表示算法在n個節點中的運行時間；Sn表示加速比，Sn越大，說明算法的并行化效率越高。

2) 推薦非空率

推薦非空率是指在用戶訪問的所有項集中，能夠給出有效推薦的被訪問項集的比例，是一種對關聯規則算法挖掘的頻繁項的有效性進行評價的指標，能夠對算法挖掘的所有頻繁項的總體質量進行評估。推薦非空率的定義為

其中，UI 為用戶訪問的所有頻繁項集的集合，RI 為給出了有效推薦的項集的集合，RecNon 為推薦非空率。

4.4 算法可行性分析

為驗證MR-PARIMIEG 算法、FPM-HCG[8]、IncbuildingPFP[10]算法在大數據環境中進行頻繁項集挖掘的可行性，以及LZO 壓縮算法對運行效率的有效提升，以加速比作為衡量指標，應用上述3 種算法以及不使用LZO 數據壓縮技術的MR-PARIMIEG(NOLZO)分別對上述4 個數據集進行處理。同時，為確保實驗結果的準確性，各算法對每個數據集進行處理時均運行10 次，并取最后運行時間的平均值作為實驗結果，然后計算加速比。最終的實驗結果如圖4 所示。

從圖4 中可以看出，在處理RetailRocket、Susy和Jester 這樣規模相對較大的數據集時，各算法運行的加速比隨著節點數的增加而逐漸增加，并且MR-PARIMIE 始終具有最高的加速比，而未進行數據壓縮的MR-PARIMIEG(NOLZO)的加速比始終小于MR-PARIMIE。但在處理Accident 這樣規模相對較小的數據集時，僅有MR-PARIMIEG、IncbuildingPFP 的加速比在MapReduce 節點數為2時分別達到了1.09 和1.03，而在其他情況下各算法的加速比均隨著節點數的增加而不斷降低并且始終小于1。這是因為各算法在對Accident 這樣規模相對較小的數據集進行并行化處理時，將數據分布到各個計算節點會導致各節點間的通信時間開銷快速增長，而通過并行化運算獲得的運行速度提升卻極其有限。而在處理RetailRocket、Susy 和Jester這樣規模相對較大的數據集時，各算法的加速比隨著節點數的增加而逐步上升。特別是在Susy 和RetailRocket 中，MR-PARIMIEG 的加速比在節點數為5 時最高達到了2.35 和2.23，相比于節點數為1時分別提升了1.35 和1.23，相較于未進行數據壓縮的 MR-PARIMIEG(NOLZO)分別提升了 0.14 和0.26。這是因為在規模相對較大的數據集中，各算法通過高效的并行化運算減少總體運行時間的優勢被逐漸放大，并且MR-PARIMIEG 所采用的LZO數據壓縮技術通過加快Map、Reduce 階段的數據傳輸過程有效地提升了算法的加速比。這說明MR-PARIMIEG、FPM-HCG 和IncbuildingPFP 算法適用于對規模相對較大的數據集進行并行化處理，并且MR-PARIMIEG 使用的LZO 數據壓縮技術能有效提升算法運行效率。

圖4 各算法處理各數據集的加速比

4.5 算法性能比較分析

1) 運行時間比較

將 MR-PARIMIEG 分 別 與 FPM-HCG、IncbuildingPFP 算法在RetailRocket、Susy 和Jester數據集中進行對比實驗，實驗比較了MR-PARIMIEG、IncbuildingPFP 以及FPM-HCG 算法在MapReduce 節點數為5 的集群中，在不同的初始支持度閾值下對數據集中的頻繁項集進行挖掘所需的時間，實驗結果如圖5 所示。

從圖5 可以看出，在對不同數據集的頻繁項進行挖掘時，各算法的運行時間隨著支持度閾值的增大而快速減少，MR-PARIMIEG 在3 個數據集中始終具有最少的運行時間，并且支持度閾值越小，MR-PARIMIEG 相較于FPM-HCG、IncbuildingPFP在運行時間上的優勢越明顯。而當支持度閾值達到相對較高的數值時，各算法的運行時間差異并不明顯。在數據分布較離散且相似項較多的RetailRocket數據集中（如圖5(a)所示），當初始支持度閾值為0.05 時，MR-PARIMIEG 的運行時間相比于IncbuildingPFP 和FPM-HCG 分別降低了28.05%和21.27%。隨著數據集規模的增長，在處理數據項長度相差較小的Susy 數據集中（如圖5(b)所示），當初始支持度閾值為0.05 時，MR-PARIMIEG 的運行時間相比IncbuildingPFP 和FPM-HCG 分別降低了33%和22.15%。在Jester 這樣數據較連續的數據集中（如圖5(c)所示），當初始支持度閾值為0.05 時，MR-PARIMIEG 的運行時間相比于IncbuildingPFP和FPM-HCG 分別降低了30.58%和27.74%。產生這種結果的主要原因如下。首先，MR-PARIMIEG采用了SIM-IE 策略來合并數據集中的相似項，通過減小數據集規模來加快后續Can 樹結構的構造；其次，MR-PARIMIEG 在并行挖掘頻繁項集時，所采用的并行LZO 數據壓縮算法會對數據規模進行有效的壓縮，從而顯著加快了Map 與Reduce 階段的數據傳輸過程；最后，MR-PARIMIEG 使用了DST-GA 策略，根據具體的待挖掘增量數據設置相對合適的動態支持度閾值，并由此進行后續的增量頻繁項集挖掘，在一定程度上避免了過多的頻繁項集挖掘導致的時間消耗，從而減少了總體的算法運行時間。當支持度閾值設置為相對較大的數值時，滿足該閾值的頻繁項數量極少，因此各算法對數據集進行處理的運行時間差距較小。

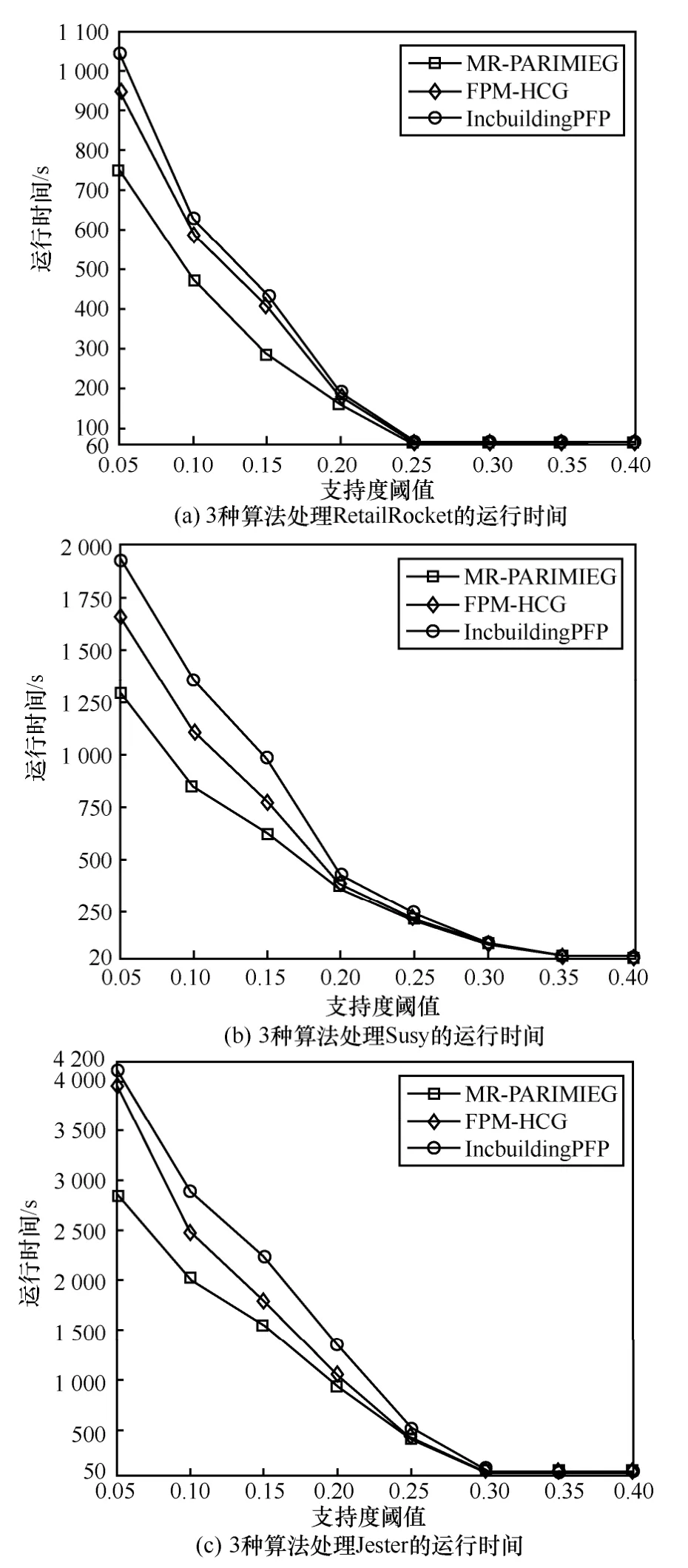
圖5 3 種算法處理各數據集的運行時間

2) 內存占用比較

將MR-PARIMIEG 算法分別與FPM-HCG、IncbuildingPFP 算法在RetailRocket、Susy 和Jester這3 個數據集中進行對比實驗，實驗比較了各算法在不同的初始支持度閾值下對數據集進行挖掘的內存占用，實驗結果如圖6 所示。

圖6 3 種算法處理各數據集的內存占用

從圖6 可以看出，隨著支持度閾值的增大，各算法的內存占用不斷下降，并且在3 種算法中，MR-PARIMIEG 在處理各數據集時始終具有最低的內存占用。在處理數據分布較離散的RetailRocket且初始支持度閾值為0.4 時，MR-PARIMIEG 的內存占用相比IncbuildingPFP 和FPM-HCG 分別降低了36.7%和41.86%；在處理數據比較連續的Jester且初始支持度閾值為0.4 時，MR-PARIMIEG 的內存占用相比IncbuildingPFP 和FPM-HCG 分別降低了33.04%和42.73%；在處理數據規模相對最大的Susy 且初始支持度閾值為0.4 時，MR-PARIMIEG 的內存占用相比IncbuildingPFP 和FPM-HCG 分別降低了40.6%和43.45%。這一方面是因為MR-PARIMIEG采用了SIM-IE 策略合并數據集中的相似項，使根據合并相似項的數據集生成的樹結構的內存占用有明顯的降低；另一方面則是因為在算法的并行化頻繁項集挖掘階段，使用了并行LZO 數據壓縮算法對Map端輸出數據進行壓縮，在數據量不變的情況下有效地減小了傳輸的數據規模，降低了最終的內存占用。IncbuildingPFP 算法雖然使用了分布式的方式對數據進行并行化挖掘，但并未解決Can 樹結構存儲所有的數據信息而導致的空間占用過大的問題，導致算法最終的內存占用過大。FPM-HCG 算法使用了滑動窗口技術來加快數據項查找過程，但會使用額外的數據表來存儲所有的已遍歷數據項信息，這會導致在最終生成的樹結構規模相同的情況下，還需要額外的內存空間來存儲這些表結構，最終造成FPM-HCG 在處理各數據集時均有最多的內存占用。

3) 頻繁項數量比較

為了進一步有效地驗證MR-PARIMIEG能夠提高對頻繁項的挖掘效率，并且具有相對較好的性能表現，在對各數據集處理的運行時間以及內存占用進行比較的基礎上，對各算法在不同的初始支持度閾值下生成的頻繁項數量進行了對比實驗，實驗結果如圖7 所示。

圖7 3 種算法對各數據集進行處理生成的頻繁項數量

從圖7 可以看出，各算法挖掘的頻繁項集數量隨著支持度閾值的增大而逐漸減少。當支持度閾值相對較小時，FPM-HCG 算法和IncbuildingPFP 算法所挖掘的頻繁項集數量多于MR-PARIMIEG 算法；當支持度閾值逐漸增大時，MR-PARIMIEG 算法挖掘的頻繁項集數量反而多于其他2 種算法；在初始支持度閾值相對較大時，各算法所挖掘的頻繁項數量差距極小。其中，在對RetailRocket 進行處理時，當初始支持度閾值為0.05 時MR-PARIMIEG 所挖掘的頻繁項數量相較于FPM-HCG和IncbuildingPFP分別減少了17.74%和23.88%；當初始支持度閾值為0.25 時，則分別增加了134.58%和139.57%。在對Susy 進行處理時，當初始支持度閾值為0.05 時，MR-PARIMIEG 所挖掘的頻繁項數量相較于FPM-HCG 和IncbuildingPFP 分別減少了16.41%和20.43%；當初始支持度閾值為0.2 時，則分別增加了35.43%和24.64%。在對Jester 進行處理時，當初始支持度閾值為0.05 時，MR-PARIMIEG 所挖掘的頻繁項數量相較于FPM-HCG和IncbuildingPFP分別減少了22.43%和27.48%；當初始支持度閾值為0.2 時，則分別增加了 31.33%和 42.58%。這是因為MR-PARIMIEG 在所指定的初始支持度閾值較小時，在增量挖掘階段通過DST-GA 策略獲得了相對較大的閾值進行增量挖掘；而當所指定的初始支持度閾值逐漸增大時，DST-GA 策略在增量挖掘階段又根據數據集信息設置了相對較小的閾值，最終根據該動態閾值獲得了相對最多的頻繁項數量。在初始支持度相對較大時，由于滿足閾值的頻繁項數量極少，因此各算法所挖掘的頻繁項數量差距較小。同時，通過對比圖5～圖7 可以看出，即使是在支持度閾值逐漸增加的情況下，需要對更多的數據進行處理以挖掘相對較多的頻繁項集時，MR-PARIMIEG 的運行時間和內存占用依然有著相對最優的表現，這也有效證明了MR-PARIMIEG 具有最佳的頻繁項挖掘效率。

4) 推薦非空率比較

為了驗證MR-PARIMIEG 算法采用的DST-GA策略通過動態設置支持度閾值以挖掘更多高質量頻繁項集的有效性，在比較各算法挖掘的頻繁項數量的基礎上，將推薦非空率作為評價指標對所挖掘的頻繁項質量進行了比較，實驗結果如圖8 所示。

從圖8 可以看出，在對各數據集進行處理時，MR-PARIMIEG 所挖掘的頻繁項始終有著最佳的推薦非空率，并且支持度閾值越小，其推薦非空率的優勢相較于IncbuildingPFP 和FPM-HCG 越明顯。其中，在RetailRocket 中，當初始支持度閾值為0.05時，MR-PARIMIEG 的推薦非空率相比FPM-HCG和IncbuildingPFP 分別增加了0.11 和0.13；在Susy中，當初始支持度閾值為0.05 時，MR-PARIMIEG的推薦非空率相比FPM-HCG 和IncbuildingPFP 分別增加了0.13 和0.15；在Jester 中，當初始支持度閾值設置為0.05 時，MR-PARIMIEG 的推薦非空率相比FPM-HCG 和IncbuildingPFP 分別增加了0.07和0.12。這是因為MR-PARIMIEG 采用了DST-GA策略，根據數據集信息實時對支持度閾值進行調整。當支持度閾值較小時，DST-GA 在增量挖掘階段通過設置相對較大的閾值對冗余的無效頻繁項集進行了剪枝；當支持度閾值逐漸增大時，又通過設置相對較小的閾值對數據集中的有效頻繁項集進行了挖掘。因此，MR-PARIMIEG 對各數據集進行處理所產生的頻繁項集始終具有相對較高的推薦非空率，即MR-PARIMIEG 采用的DST-GA 策略根據數據信息以及初始的支持度閾值動態調整閾值大小，既避免了初始支持度閾值較小時挖掘過多的無用頻繁項集，又避免了過大的初始支持度閾值導致的有效頻繁項丟失，使最終挖掘的頻繁項集具有較高的質量。

圖8 各算法挖掘頻繁項的推薦非空率

5) Map 與Reduce 階段數據傳輸時間比較

為驗證本文所采用的并行LZO 數據壓縮算法的有效性，將MR-PARIMIEG 分別與Optimized-MR[13]、COID-MR[14]進行對比實驗，比較各算法在MapReduce 集群中對各數據集進行處理時，在不同的內存區閾值下Map 與Reduce 階段的數據傳輸時間。同時，為保證實驗結果的準確性，MR-PARIMIEG在該實驗中不使用SIM-IE 策略對數據集中的相似項進行合并，確保各算法在處理同一數據集時Map端輸出的總數據規模相同。實驗結果如圖9 所示。

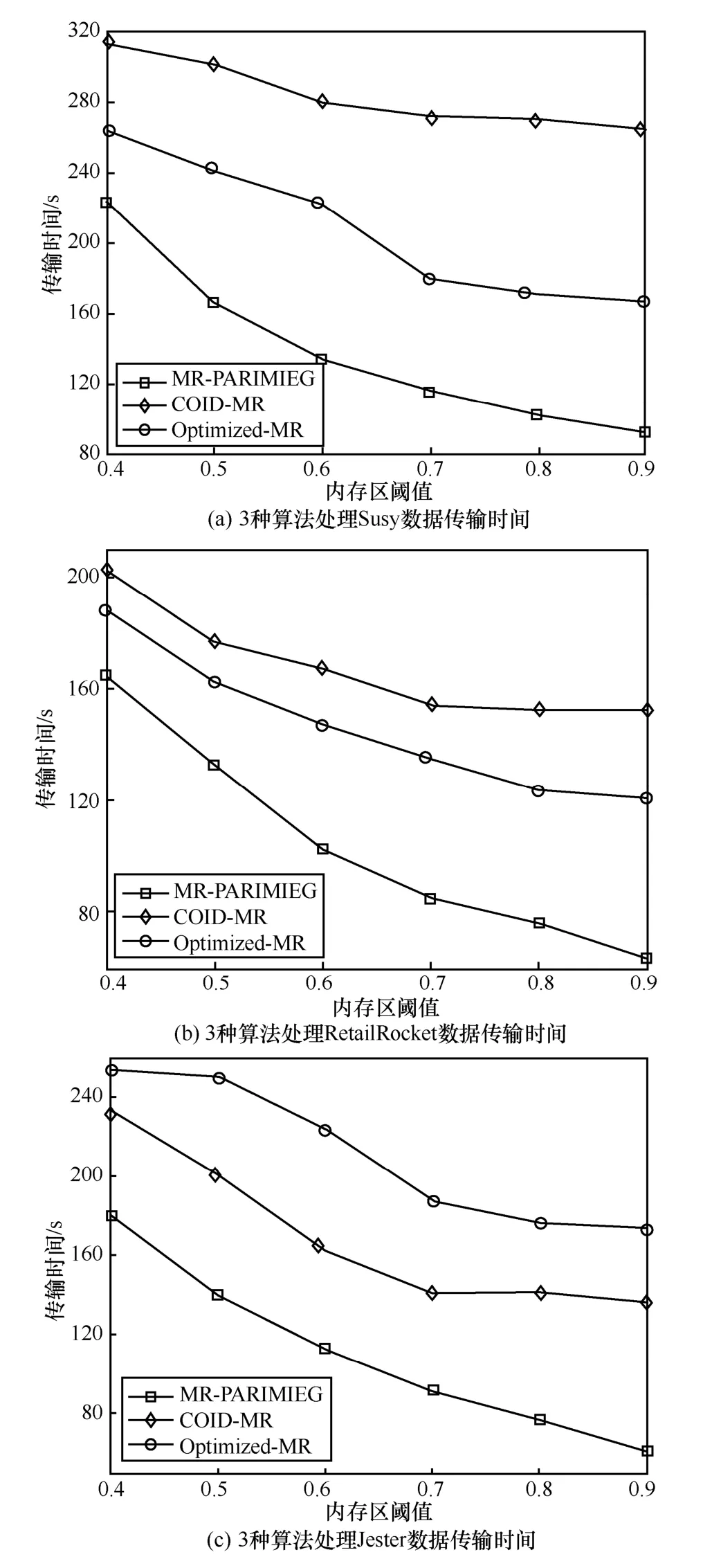
圖9 3 種算法處理各數據集的數據傳輸時間

從圖9 可以看出，使用并行LZO 數據壓縮技術的MR-PARIMIEG 算法在處理各數據集時，Map與Reduce 階段的數據傳輸過程始終耗時最少，并且隨著內存區閾值的增加，MR-PARIMIEG 的優勢愈加明顯。在對Susy 進行處理且內存區閾值設置為0.9 時，MR-PARIMIEG 的數據傳輸時間相比Optimized-MR 和COID-MR 分別減少了43.98%和64.82%；在對RetailRocket 進行處理且內存區閾值設置為0.9 時，MR-PARIMIEG 的數據傳輸時間相比Optimized-MR 和COID-MR 分別減少了47.11%和58.17%；在對Jester 進行處理且內存區閾值設置為0.9 時，MR-PARIMIEG 的數據傳輸時間相比Optimized-MR 和COID-MR 分別減少了64.17%和54.42%。這是因為并行LZO 數據壓縮采用了多線程技術，可以在單位時間內極大地提高數據壓縮效率，并且對于數據大小的壓縮率通常可以達到50%左右，因此可以通過減少傳輸的數據規模來有效地提升數據傳輸速度，而數據在內存中的解壓縮過程所消耗的時間與數據在磁盤與內存間進行傳輸所消耗的時間相比基本可以忽略不計。因此，MR-PARIMIEG 在對各數據集進行處理時，Map 和Reduce 階段的數據傳輸過程有著較少的時間消耗。

同時，從圖9 還可以看出，在對Susy 和RetailRocket 進行處理時，Optimized-MR 的表現好于 COID-MR ；在對 Jester 進行處理時，Optimized-MR 卻有著相對最差的性能表現。這是因為Susy 和RetailRocket 這類數據活躍度相差較小，并且在Map 端每次產生的數據規模也相對較小，因此當內存區閾值較小時，Optimized-MR 每次進行磁盤與內存間的I/O 操作所能傳輸的數據量隨著內存區閾值的增加而快速增長，最終有效加快了數據傳輸速率；而Jester 這類數據活躍度相差較大，COID-MR 所使用的基于數據活躍度的分類方式可以有效地對數據進行分類來優化傳輸流程，從而加快數據傳輸。相較于Optimized-MR 和COID-MR，MR-PARIMIEG使用的并行LZO數據壓縮算法的數據壓縮過程不受Map 端輸出數據規模以及數據活躍度影響，并且在集群中其并行化壓縮效率得到了極大地提升。因此，MR-PARIMIEG 的Map 與Reduce 階段的數據傳輸過程始終有著最少的時間消耗。

5 結束語

針對傳統的關聯規則算法在大數據環境下的不足，本文提出了一種并行關聯規則增量挖掘算法MR-PARIMIEG。首先，該算法提出了結合信息熵的相似項合并策略SIM-IE 來對數據集中的相似項進行合并，以降低最終生成的Can 樹結構的復雜度以及空間占用；其次，使用DST-GA 策略獲取動態支持度閾值，并根據動態閾值進行關聯規則挖掘，從而避免了冗余的頻繁模式挖掘，提高了后續挖掘關聯規則的速度與質量；最后，將頻繁項集挖掘過程向MapReduce 分布式計算平臺遷移以并行化處理大數據集，同時使用并行LZO 數據壓縮算法對Map 端輸出數據進行壓縮以加快Map 與Reduce 階段之間的數據傳輸過程，最終提高算法的運行速度。為了驗證MR-PARIMIEG 的性能，本文設計了相關實驗，在RetailRocket、Susy 以及Jester 這3 個數據集中將MR-PARIMIEG 分別與FPM-HCG、IncbuildingPFP 進行比較。最終的實驗結果與分析均反映出與其他基于Can 樹結構的并行化算法相比，本文提出的MR-PARIMIEG 在處理大數據集時具有相對較好的性能表現，這也證明了MR-PARIMIEG 的優越性。