深部暫停開采礦井采空區積水過程分析

易偉功

(長沙礦山研究院有限責任公司， 湖南 長沙 410012)

0 引言

隨著深部資源枯竭而礦區暫停開采或者礦井停采閉坑，可能會出現如水體污染、地面塌陷、土地破壞、采空區積水等一系列地質災害和環境問題，分析深部暫停開采礦井的采空區積水過程，對礦井淺部殘留礦體的回收安全具有重要意義[1?2]。國內外學者對煤礦廢棄礦井和采空區積水的系統模型和積水過程進行了大量的研究。周建軍等[3]通過對廢棄礦井的含水介質及其地下水運動規律進行分析，建立了水流運動概念模型，并提出數值模擬方法和技術，為廢棄礦井的恢復及災害治理提供了依據；張壯路等[4-5]通過對唐村煤礦水文地質條件和礦井廢棄后地下水動力模式分析, 分析了水位回彈過程中礦井的容水空間及其分布特點, 分析了廢棄礦井水位回彈的時空過程和最終動態平衡模式。YOUNGER P.L.等[6]依據廢棄礦井中井巷工程和采空區中含水介質和水動力場特征的區別，將礦井含水區域劃分為紊流管道區、低滲透性層流區和高滲透性層流區，并建立了3種廢棄礦井采空區積水系統模型；BANKS D.等[7?8]引入有效面積的概念，建立了積水體積可變、水頭可變的地下水回灌模型，并對觀測井中的水位變化進行了成功預測。獅鳳山銅礦深部資源暫無開采價值，故決定暫停九中段以下所有開采活動，集中回收九中段以上邊角礦體，由于深部排水系統拆除后，地下水會隨著回升，本文以獅鳳山銅礦為研究背景，在綜合考慮國內外研究現狀的基礎上，根據獅鳳山銅礦礦區水文地質條件，分析獅鳳山銅礦深部暫停開采后采空區的積水過程。

1 深部暫停開采后采空區積水體積

根據礦山現有采礦和地質資料整理分析，采用回采空間法針對井下主要巷道和采空區的體積計算出積水體積。積水體積（容積）是指積水標高h以下的礦井充水體積的總量。礦井容水空間（介質）由井巷工程、采空區及裂隙帶、未采動巖石裂隙系統組成。其中井巷和采空區及裂隙帶空間由開采活動形成，是礦井容納積水的主要空間，本次主要是以采空區容積和開拓巷道的體積之和作為計算的積水體積。

根據資料，獅山礦段1965年水文地質勘探時期測定的地下水位標高為1230m～1228m，但由于礦區幾十年對地下水的排泄和居民用水對地下水的消耗等原因，其積水標高在短時間內不會高于綠汁江最低侵蝕面（標高在1205m左右），根據對礦區采空區調查及統計結果，十中段至十八中段的空區體積為1566.9萬m3，其中采空區體積為1508.0萬m3，巷道體積為58.9萬m3，見表1。

根據現場對采空區的調查發現，礦區中大部分采空區已被碎石充填，礦區中采空區的充填率約為90%，碎石充填體的空隙率可按45%計算，經綜合計算，采空區容積為采空區體積的50.5%，因此，十中段至十八中段的總積水體積為820.5萬m3，其中采空區容積為761.6萬m3，巷道積水體積為58.9萬m3，見表2。

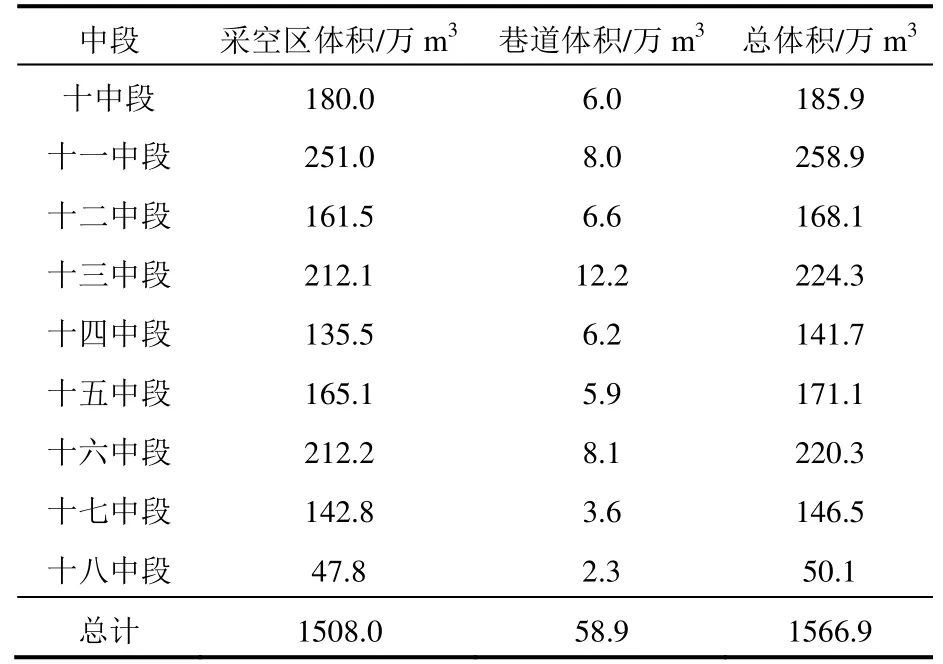
表1 各中段體積計算統計

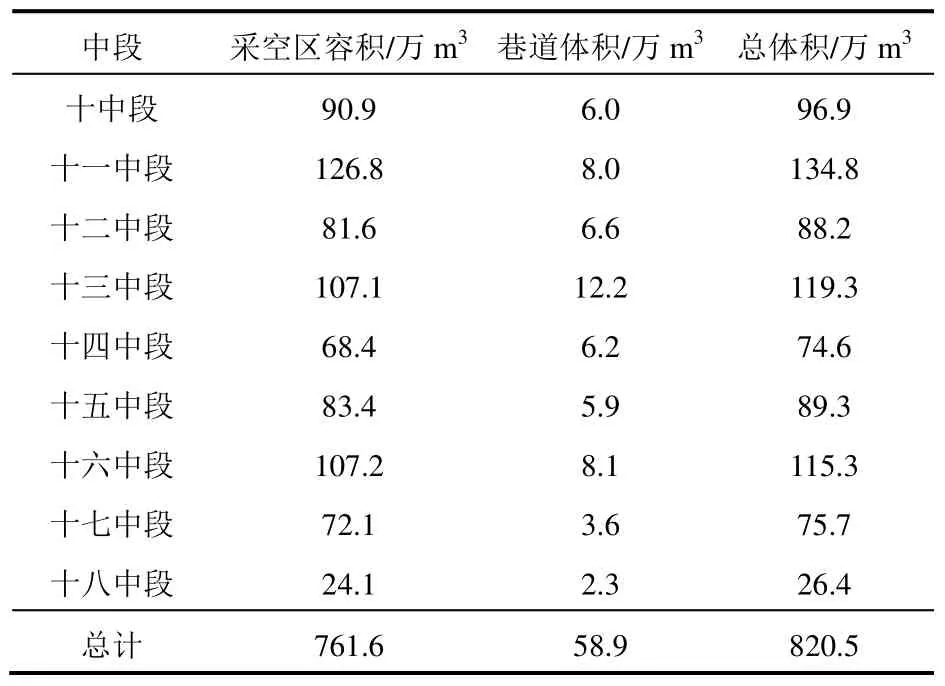
表2 各中段積水體積計算統計

2 積水過程分析

2.1 積水恢復過程分析

礦井停止排水后，首先是井下最深部積水，積水會以較快的速度升高，達到一定高度后，在水壓差作用下通過不同形式向低標高相鄰區段滲透和徑流，隨著積水高度增加，水力梯度逐漸減小，導水通道增多和滲透面積增大，水位上升的速度越來越慢，最終達到礦區內地下水動態平衡狀態。

礦區采空區積水的主要來源是昆陽群綠汁江組含水層的補給量約33000m3/d，以及礦區上部垮落區雨季補給量約928m3/d。將九中段以下排水系統撤離后，地下水會隨著上升，在一定時間內會形成一定標高之下的積水靜貯量。由于礦床東部和西南部均為隔水邊界，且昆陽群綠汁江組鳳山段是礦區的唯一含水層，因此，礦井積水在一定標高之下滲透途徑主要有：昆陽群綠汁江組鳳山段白云巖含水層的自然滲透；采礦作用后礦巖柱松動裂隙帶和其他裂隙的滲透；極端條件下軟巖潰破引起的滲透。

礦井在積水初期其補給量遠大于滲透量，積水速率較快，隨著時間的推移，導水通道和滲透的面積也相應的增多，積水速率會越來越小，最終當礦井補給量與滲漏量相當時，礦井積水將會趨于一種動態的平衡。

2.2 積水恢復標高計算

獅鳳山礦區主要含水層為潛水含水層，在九中段以下礦井排水設備拆除后，礦區地下水只能通過含水層的自然滲透。隨著時間的推移，礦區地下水的最終潛水位與礦區原始潛水位基本持平或者略低于原始潛水位，但由于礦井開采的過程中人為對地下水進行了大量排泄，消耗了大量的地下水，整個地下水流場都發生了很大的變化，在較短時間內地下水很難恢復到原始水位。故本次計算的積水標高是在一定時間周期內的一個相對值，主要是以礦井內滲出和涌入的水量相等時經歷的時間值，即基本達到地下水相對動態平衡狀態時的相對積水標高值作為積水恢復標高。

本文根據水均衡原理和達西定律計算積水恢復標高，積水恢復過程中拐點標高是指礦井地下水的補給量和排泄量基本相等時，積水高度相對穩定的一個動態平衡，其計算公式如下：

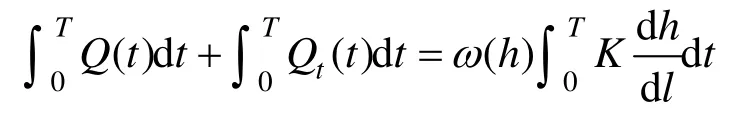
根據資料分析，目前白云巖水源滲漏穩定補給量在33000m3/d，而其他上部垮塌區的補給量約928m3/d，根據地下水運動規律，在較低積水標高時白云巖水源滲透補給量可近似保持不變，但二者之和不大于33928m3/d，為了安全起見取33928m3/d，因此有：

式中，dl為含水層厚度，m；k為含水層滲透系數，m/d；ω(h)為過水斷面面積，m2；h為水頭差，m。

九中段以下最大的積水面積為99646m2，假設拐點積水高度為H，則根據積分計算可得：

lnH=5.87，則H=354.25m≈354m。

按十八中段最低底板標高為745m計算，則積水恢復過程中拐點標高約為1099m，即基本接近于鳳山十一中段（1108m）標高。

2.3 水位恢復時間計算

利用礦山現有資料，統計分析了礦山在開采過程中歷史水位的變化情況（見圖1）。通過圖1可知：礦區地下水位在礦山開采的初期，由于礦坑涌水量較小，其水位保持較平緩的波動并緩慢下降，隨著礦山開采深度向下延伸，揭露的導水裂隙增多，加大地下水壓，增加相應的井下涌水量，地下水位的下降趨勢也明顯地增大，隨著較長時間疏排礦坑涌水，水位曲線逐漸平緩。

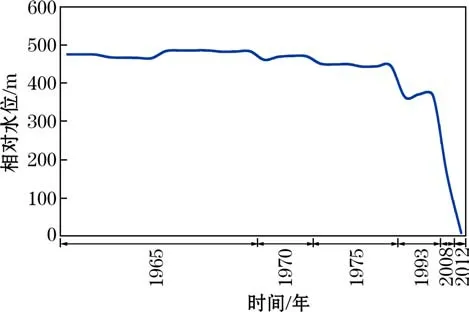
圖1 礦區水位歷時變化曲線

根據資料統計九中段以下各中段的積水面積（見表3），依據地下水的運動規律和礦區開采過程中的實際情況，在較低標高位置其涌水量基本穩定，隨著積水高度增高，滲水面積逐漸增加，其礦坑水位回升上漲的速率也呈現出逐漸減少的規律。利用曲線擬合法確定出積水高度h與時間t的關系，得出：

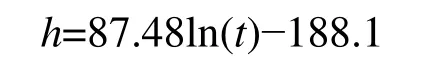
其相關系數為0.96，積水回升歷時變化曲線如圖2所示。

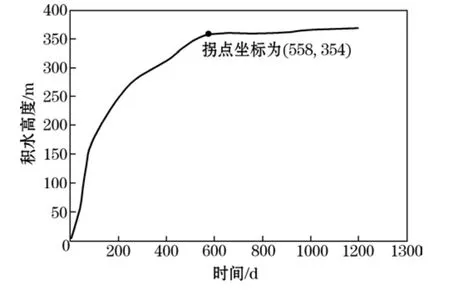
圖2 積水回升歷時變化曲線

深部礦床暫停開采，排水設備全部拆除后，根據圖2可計算得出，礦坑地下水回升到拐點標高1099m時需要的時間約為558d；隨著時間的推移，礦區地下水位將繼續緩慢上漲，上漲至當地侵蝕基準面（標高為1205m），水位恢復需要的時間為1650d。另外，以鳳山十八中段最低底板標高（745m）為基礎，計算出地下水位恢復至各中段水平所需時間，見表4。

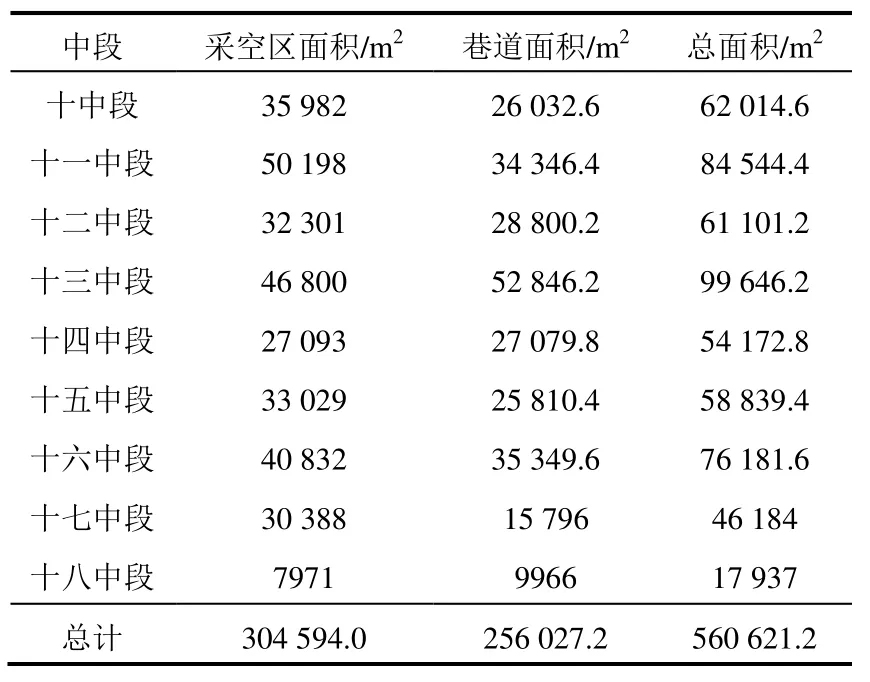
表3 各中段積水面積

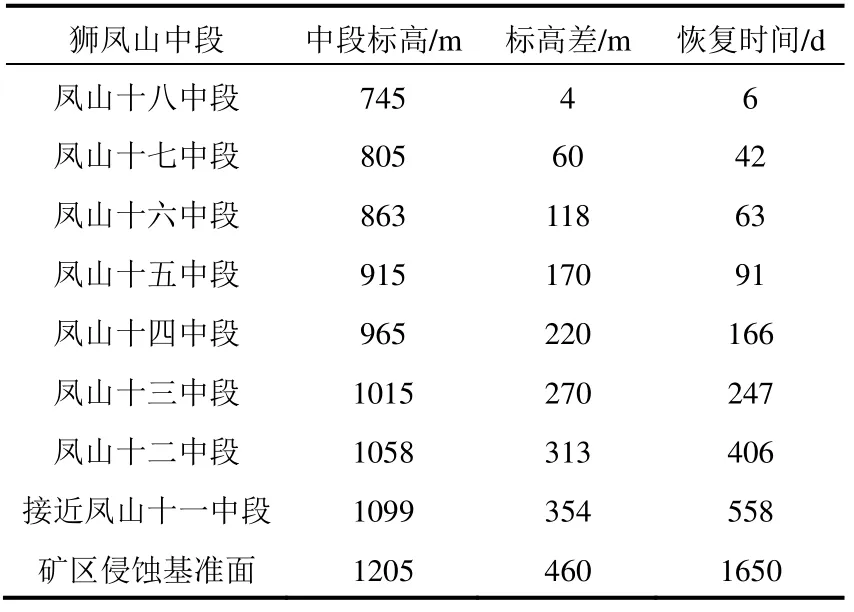
表4 恢復至各中段水平時間計算

3 結論

（1）礦井停止排水后礦區中的水動力學特征是一個集層流和紊流為一體的復雜流體。礦床內含水介質空隙具有多級次的特征，地下水在介質中的流動具有時間性較強及階段性較分明的運動規律。

（2）本次統計計算了十中段至十八中段的積水體積，總積水體積為820.5萬m3，其中采空區容積為761.6萬m3，巷道積水體積為58.9萬m3。

（3）運用水均衡原理和達西定律相結合的穩定流計算方法，計算得出礦坑地下水回升過程中拐點標高約為1099m，基本接近于鳳山十一中段（1108m）標高；并計算得出恢復到該標高所需要的時間約為558d；礦坑地下水位恢復到當地侵蝕基準面（1205m）時，所需要的時間約為1650d。根據礦床開采期間地下水位下降的曲線與暫停開采地下水位上升的曲線基本相符的特征，進一步論證計算結果基本符合實際。