基于改進LSTM模型的農產品短期價格預測方法

張保國 任萬明 吳兵

(1山東麥港數據系統有限公司山東濟南250100;2山東省現代農業農村發展研究中心山東濟南250100;3濟南市農業農村信息中心山東濟南250100)

農業是國民經濟的基礎，農產品市場是我國市場經濟的重要組成部分，農產品價格的波動直接關系農民切身利益乃至國民生活質量。農產品短期價格受自然災害、重大疫情等的影響，農產品短期價格呈現波動大、非平穩、非線性的特點，這對農民的收入和農產品市場的穩健發展等產生不利的影響。因此，對農產品短期價格進行預測，幫助政府做出相關決策實施宏觀調控、對農業從業者進行指導、維持農產品市場的穩健具有重要作用。

根據原理不同，農產品短期價格預測可以分為2種：定性預測方法和定量預測方法［1］。定量預測方法是農產品短期價格預測領域的主流方法，又可以分為傳統方法和智能方法兩大類。傳統方法主要指計量經濟方法，其中比較流行的有差分整合移動平均自回歸（Autoregressive Integrated Moving Average，ARIMA）模型［2-3］、自回歸條件異 方 差（Autoregressive Conditional Heteroscedasticity，ARCH）模型［4-5］、線性回歸等。經濟計量模型普遍對非線性數據預測具有局限性，對數據使用有太多限制。智能方法中比較普遍使用的有人工神經網絡［6-8］、遺傳算法［7］等。目前，在農產品短期價格預測方面，遺傳算法主要是與其他預測方法組成混合模型來使用，但是遺傳算法中參數的選擇主要是靠經驗來選擇，而參數的人為選擇很容易對預測結果造成不利影響。

總體來看，農產品價格的影響因素大概可以分為2種：內部因素和外部因素。內部因素主要是人們按照以往的價格來定價，這使得農產品價格序列表現為歷史相關性；而外部因素則由國民經濟體中其他的市場變動、自然災害、重大疫情等情況引起，這使得農產品短期價格序列表現為波動大、非平穩、非線性的特點。

劉峰等［9］利用農產品價格時間序列的當前值和過去值準確預報未來值，以白菜價格為例，構建了非平穩時間序列ARIMA（p，d，q）。姚霞等［10］以南京市青椒價格為例，構建了非平穩時間序列ARIMA（p，d，q）模型，描述并預測時鮮農產品價格的動態變化。但是ARIMA模型過于依賴數據的穩定性，它本質上只能捕捉線性關系，不能捕捉非線性關系，在面對非線性時間序列時，ARIMA模型則差強人意。

馬孝斌等［11］對影響生豬市場價格的幾個關鍵因素進行關聯分析，在此基礎上建立了生豬市場價格預測的向量自回歸模型，并運用此模型對實際數據進行了預測和分析。蘇博等［12］在對中國糧價的研究中，運用回歸分析模型分析了影響中國糧價運行的影響因子，并結合中國糧食價格定價和作用機制在不同時期的發展變化，運用逐步回歸方法構造出了糧價預測模型。但是回歸分析對數據的異常值十分敏感，并且難以對數據的異常值和大幅波動進行處理。

羅萬純等［13］利用GARCH、GARCH-M、TARCH和EGARCH等ARCH類模型對糧食價格的波動、波動的非對稱性進行了分析，并提出了對糧食價格預測的建議。董曉霞等［8］使用雙指數平滑、Holt-W inters無季節性模型和ARCH模型對我國鮮奶零售價格短期預測進行了應用模擬，結果顯示，ARCH模型預測結果精確度最高。但是ARCH模型對參數的限制極其嚴格，而且ARCH模型會過高估計抖動率。

牛東來等［14］以北京市2015—2017年幾個街道的雞蛋價格為數據集，以過去5 d的價格作為輸入，使用基于Levenberg-Marqardt的BP算法，有效克服了標準BP算法收斂速度緩慢、過擬合等不良現象，總體上對檢驗樣本的數據具有很好的擬合效果。張津等［15］利用神經網絡的很強的非線性、自組織、自學習能力，選用基于時間序列的BP神經網絡預測法，對豬肉的價格進行預測。但是普通神經網絡雖然可以有效的擬合數據，但是它并沒有對起伏尖銳的大幅的、不正常的波動數據進行處理，在這方面它存在著不足。

易利容等［16］提出了一種基于多變量分析的LSTM時序預測方法，該方法利用數據的遠距離信息和多變量相關性，有效地提高了工業傳感器時序數據預測的準確性。但是，農產品短期價格波動頻繁，數據異常值和大幅波動對預測精度影響極大，該模型難以對其進行處理。

Kyunghyun等［17］提出了區別于LSTM的另一種門控循環單元（GRU）的門控機制，目標是讓每個經常性單位自適應捕捉不同時間尺度的依賴關系，Chung等［18］也對GRU進行了具體的研究。但該思想也難以結合數據異常波動和大幅波動來對數據進行處理。

農產品的價格受到內部外部多方面的影響，呈現出波動大、非線性、非平穩的特點，而劇烈起伏的波動往往對預測結果產生不好的影響，但是目前現有的方法難以對起伏尖銳的、大幅的、不正常的波動數據進行處理。對此，本文針對農產品價格的歷史相關性，使用LSTM來解決，其次，針對由自然災害等引起的大幅波動，可以使用價格波動數據來降低其影響。因此，考慮對標準的LSTM模型進行改進，提出一種新的W-LSTM模型，輸入價格數據和波動數據來訓練模型，來減少異常價格波動和大幅波動對預測結果的影響，實現對農產品短期價格的精準預測。

1 W-LSTM模型

1.1 數據預處理

由于農產品的價格受到歷史價格及其價格波動的影響，因此，進行如下定義：

定義t為歷史相關天數：xi表示第i天的價格數據，則輸入數據為Xi={x1，x2……xt}，X2={x2，x3……xt+1}，以此類推，直到最后一天；價格波動使用公式Δpi=pi-pi-1來計算獲得，當i=1時，假定前一天的數據為0，則Δw1=w1，價格波動的輸入格式為ΔPi={Δp1，Δp2……Δpt}，ΔP2={Δp2，Δp3，……Δpt+1}，以此類推，直到最后一天。

1.2 模型定義

LSTM模型的輸入包括歷史價格數據和歷史價格波動數據，即使用前t天的數據作為輸入來預測t+1天的價格。

LSTM是一種特殊的RNN結構，是由Hochreiter等［19］在1997年提出的，用于決定何時以及如何更新RNN的隱藏狀態，由于其很獨特的設計結構，LSTM可以很好的解決梯度消失問題，它特別適合處理時序問題。標準的LSTM單元包括遺忘、輸入、輸出門。

W-LSTM在LSTM的基礎上，將其輸入信息進行了相應的處理，將歷史價格數據和價格波動數據進行相應的處理作為數據的輸入，并且它還包括前置門、遺忘門和輸出門（圖1），因此，它相對標準LSTM能處理更多的信息，在本研究中它的輸入包含歷史價格信息和價格波動信息。

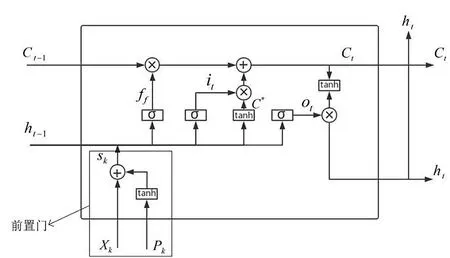
圖1 W-LSTM結構圖

前置門（Front gate），將價格信息和價格波動信息進行結合形成組合信息：

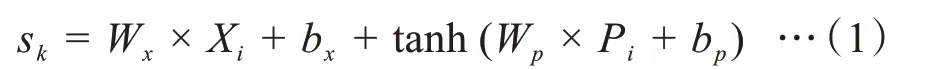
其中，Xi是價格信息用來分析歷史價格變動規律，Pi是由價格信息中提取出的價格波動信息單獨作為輸入，來強化模型對價格波動的處理，{Wx，Wp，bx，bp}是網絡參數。tanh激活函數的輸出結果在［-1，1］之間，輸出值越靠近-1，代表負波動越大；輸出值越靠近1，代表正波動越大。數據波動越大，它對W-LSTM模型的訓練影響就越大，相反，當波動為0時，輸入的波動數據便對模型的訓練無影響，此時，W-LSTM模型便相當于標準LSTM。

遺忘門（Forget gate），是控制是否“遺忘”的歷史狀態信息。

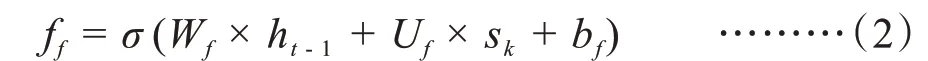
其中，ht-1是上一序列的隱藏狀態，sk是本次的輸入序列。定義Wf為ht-1的偏重矩陣，Uf為sk的偏重矩陣，bf為偏置。

輸入門（Input gate）負責將當前輸入補充到最新的“記憶”中，它包含兩個部分：第一，Sigmoid層輸出it；第二，一個Tanh層創建一個新的候選值向量，會被加入到狀態中。定義{Wt，Ut，bt}{Wa，Ua，ba}為輸入門的網絡參數，則

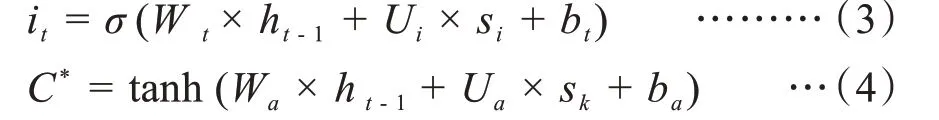
然后更新細胞狀態：

輸出門（Output gate）控制著有多少“記憶”可以用于下一層網絡的更新中，定義{Wo，Uo，bo}為輸出門的網絡參數，輸出門的計算可用公式6表示：

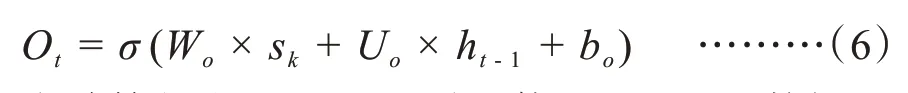
在計算得出Ot后，還需要使用Tanh函數把記憶值壓制到［-1，1］，所以最終輸出門的輸出公式為：

最后一個W-LSTM層輸出的歷史信息經過一個預測層輸出結果y：

1.3 訓練過程

W-LSTM的訓練過程如下：

按照前向計算公式（1）～（8）計算W-LSTM細胞的輸出值。

按照時間和網絡層級2個方向反向傳播，計算誤差項。

根據相應的誤差項，計算每個權重的梯度，更新權重。

重復（1）～（3），得到一組最優的參數，并保留下來。

為了防止訓練過程中過擬合，本研究使用Dropout正則化技術［20］，它在2014年由Hinton教授的團隊提出。Dropout提供了一種巧妙的方式，通過減少權重連接來增加網絡模型的泛化能力。

2 實驗

2.1 實驗設置說明

本節將通過實驗評估提出的W-LSTM模型。實驗環境為：INTEL Corei5 CPU，2.80GHz；4G內存。實驗數據為天津市2016年7月到2019年1月每天的蔬菜價格數據。每個對比實驗情況均運行10遍，取平均值。

設置了3個對比模型：

（1）W-LSTM模型，輸入歷史價格信息與價格波動信息訓練模型，進行預測。

（2）LM算法改進的BP神經網絡，只將歷史價格信息作為輸入，使用前n天的價格信息預測第n+1天的農產品價格。

（3）ARIMA模型，將農產品價格隨著時間推移而生成的數據序列視為一個隨機序列，用一定的數學模型來近似的描述這個序列。

同時，為了檢驗W-LSTM模型的普適性，使用辣椒、大蔥、韭菜和西紅柿4種價格數據進行實驗來對3種模型進行比較。

2.2 模擬比較試驗

本小結分別使用W-LSTM模型、LM算法改進的BP神經網絡和ARIMA模型來進行實驗，對預測結果的準確性判定公式使用的是均方誤差（MSE）和決定系數（R2）。

MSE和R2是評價模型準確率的常用指標，MSE是反映估計量與被估計量之間差異程度的一種度量，MSE越小代表著模型準確率越高；R2越大，自變量對因變量的解釋程度越高，自變量引起的變動占總變動的百分比高，觀察點在回歸直線附近越密集，代表模型擬合程度越高。其中n代表總樣本，Y_actual表示真實數據，Y_predict代表預測結果，Y_mean代表真實數據平均值。

通過對蒜苗價格序列進行建模預測，圖2、3分別是使用W-LSTM模型和ARIMA模型得到的預測結果與實際數據的比較。很明顯，本研究提出的W-LSTM模型預測結果更理想。

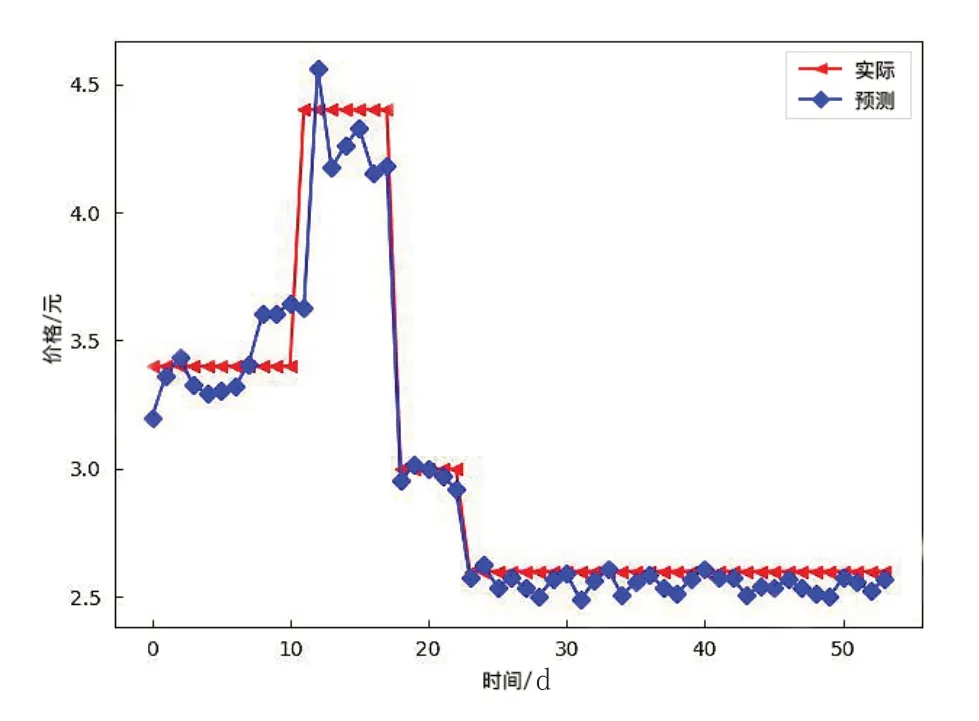
圖2 W-LSTM預測結果

通過觀察圖3數據發現，ARIMA模型的實驗結果明顯與其它模型有較大的偏差，而R2甚至小于0，這代表預測結果與原數據毫無關系。ARIMA模型在處理平穩時間序列時表現良好，當數據不平穩時，需要通過一定的處理方式得到平穩序列，而本實驗使用的蒜苗價格數據具有連續不變性和突變性，即在一段時間內連續不變，然后突然垂直變化，這種特性導致數據在差分的時候，損失了太多信息，導致ARIMA模型預測效果極其不好，偏差極大。

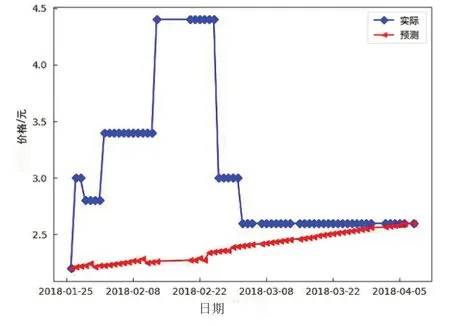
圖3 ARIMA模型預測結果

訓練結束后，輸入數據進行預測，W-LSTM模型和LM算法改進的BP神經網絡的MSE隨著預測的進行，變化如圖4所示。W-LSTM模型的MSE為0.032，LM-BP模型的MSE為0.059，ARIMA模型的MSE為0.923。W-LSTM模型的MSE比其它模型都要小，模型準確率最高；而R2比其它模型大，代表W-LSTM模型的擬合程度相對其它模型來說更高。總體來說，兩個模型的MSE變化趨勢大致相同，WLSTM模型的MSE總體上小于LM算法改進的BP神經網絡的MSE。

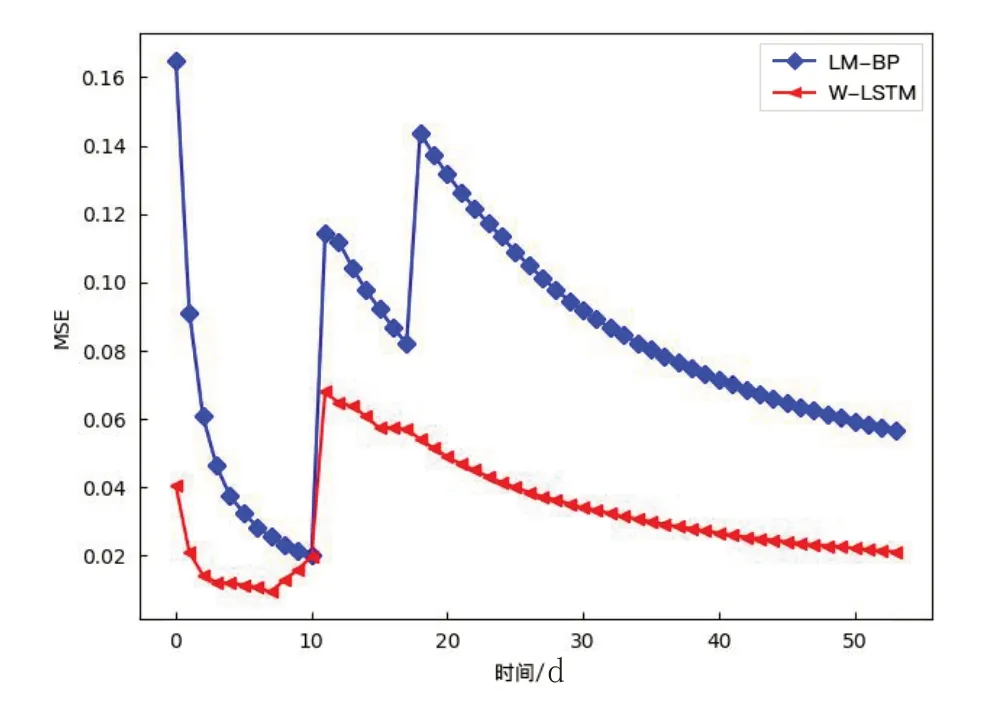
圖4 W-LSTM模型和LM算法改進的BP神經網絡的MSE變化

輸入數據在總數據的三分之一處出現了大幅的波動，而此時兩模型的MSE均出現了短暫的增長，而W-LSTM模型的MSE波動變化要小于LM算法改進的BP神經網絡，這說明W-LSTM模型對處理數據的大幅波動有著更好的效果。

為驗證W-LSTM模型的普適性，又使用辣椒、大蔥、韭菜和西紅柿4種價格數據來做為輸入對三種模型進行對比實驗，實驗結果如表1、2。表中展示了3種模型分別在四種蔬菜上的預測結果評價指數，可以看出，W-LSTM比其他模型擁有更好的效果，同時說明了W-LSTM模型具有良好的普適性。

通過以上實驗可以看出，W-LSTM模型準確率更高，擬合程度更好，同時具有良好的普適性。綜合來看，針對農產品短期價格預測問題，WLSTM是一個很好的預測模型。

表1 MSE對比

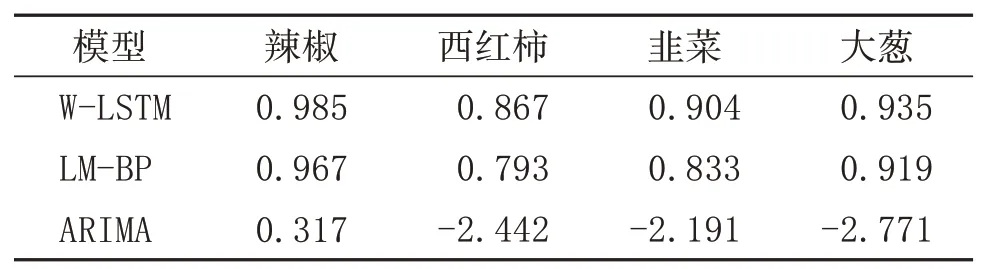
表2 R 2對比

3 結語

農產品價格與農民收入息息相關，也是國家決定相關政策的重要因素，對農產品價格進行精準預測對解決農產品供需問題，促進農業生產轉型、和市場經濟持續健康發展具有重要意義。本文針對農產品短期價格預測提出了一個W-LSTM預測模型，以歷史價格信息與價格波動信息作為輸入對模型進行訓練，實現對農產品短期價格的精準預測。首先，將W-LSTM對波動較大、不平穩的數據進行處理，實驗結果表明，W-LSTM對于該類數據具有更高的準確率；其次，將W-LSTM用于其他的農作物產品，實驗表明，該模型比以往通用預測模型在數據上有更好的普適性。

在未來，計劃將此模型應用到其他具有相同特征的預測問題，讓波動較大、不平穩不再成為預測問題上的一大障礙；同時，提高模型的適應性，讓模型可以處理更多通用問題，例如：天氣信息、重大疫情等相關信息的處理。