高壓直流系統電纜接頭中空間電荷與電場分布的仿真計算
吳 洋,朱慶東,高 路,吳 鍇
(1.西安交通大學電氣工程學院,陜西 西安 710049;2.國網山東電力公司電力科學研究院,山東 濟南 250003)
0 引言
隨著高壓直流輸電技術的發展,交聯聚乙烯(Cross?linked Polyethylene,XLPE)電纜由于其優良的性能正得到越來越廣泛的應用[1-2]。在直流高壓下,在XLPE的內部容易形成空間電荷的積聚,這些空間電荷會導致XLPE中的電場強度分布發生畸變,最終會導致電纜的擊穿[3-5]。
電纜接頭是電力電纜的重要組成部分[6-7],在電纜接頭中存在兩種不同的絕緣材料,分別是電纜主絕緣使用的XLPE 和增強絕緣使用的乙丙橡膠(Ethylene Propylene Rubber,EPR)。由于兩種材料的相對介電常數、電導率、電荷輸運參數的不同,在兩種材料的界面上會產生空間電荷的積聚,進一步加劇電纜接頭中的電場畸變[8]。
高壓直流電纜接頭復雜的結構與界面情況,使其成為電纜系統中的薄弱點,需要重點研究。受限于現有的空間電荷測量技術,對電纜接頭中空間電荷分布情況無法直接進行測量。
近年來,國內外的學者在空間電荷仿真領域展開了一系列的研究。Alison 和Hill 在1994 年首次提出采用電荷輸運模型計算研究聚合物介質材料的空間電荷積聚特性[9],他們考慮了電極-介質界面的電荷注入、電極-介質界面的無阻擋電荷抽出、定常載流子遷移率和單一能級陷阱的捕獲,沒有考慮陷阱電荷的脫陷,初步得到了交聯聚乙烯內部的空間電荷積聚特性。Roy 使用恒定遷移率的流體模型開發了一種數值模型,用于解釋聚乙烯中的電荷傳輸,包括入陷和復合的影響[10]。西安交通大學吳鍇課題組采用有限差分法求解電荷連續性方程和泊松方程,研究了試樣厚度對介質材料空間電荷積聚的影響[11]。
但是,以往的研究中,空間電荷的仿真為一維簡單模型的仿真,主要目的為研究空間電荷輸運機理,難以應用到實際工程模型中,為了研究高壓直流電纜接頭中空間電荷與電場強度分布情況,建立三維的電纜接頭仿真模型。
1 仿真理論
絕緣材料中的空間電荷積聚包含一系列復雜的過程,如載流子的注入、抽出、遷移、復合等。空間電荷的分布會影響材料中電場強度的分布,而電場強度的分布也會進一步影響空間電荷在材料中的輸運過程。這些過程相互影響,非常復雜。為實現空間電荷的仿真,對一些過程進行了合理的忽略。
1.1 雙極性載流子輸運模型
采用文獻[12]所示的基于抽出受限的雙極性載流子輸運模型,如圖1 所示。空穴從正極注入,從負極抽出;電子從負極注入、正極抽出。在介質內部,電子與空穴在電場的用下進行遷移,并發生正負載流子的復合等過程。
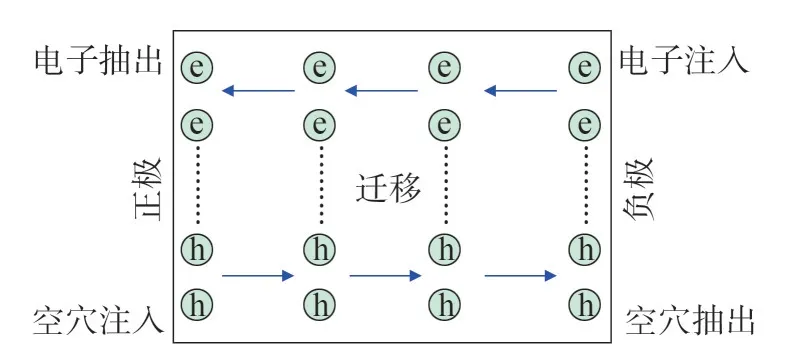
圖1 雙極性載流子輸運模型
通過3 個方程對載流子的輸運過程進行描述,如式(1)—式(3)所示。式(1)為輸運方程,式(2)為連續性方程,式(3)為泊松方程。
大量實驗證明,加速度噪聲實際上與物體的加速度有關,只有減小滑塊在變形結束時速度突變或延長速度變化所需的時間,才有可能減小加速度噪聲。此時,阻尼、隔震等噪聲控制技術均無力降噪。正因為如此,當在大型機械壓力機上完成沖裁、落料及剪切工藝時,加速度噪聲值最高,而在完成模鍛、拉深、擠壓等工藝時,在滑塊到下死點后,由于變形工件的彈性回復力,使回程初期滑塊上仍承受力的作用,而這一彈性力是逐漸減小到趨向于零,大大降低了滑塊速度變化梯度,所以加速度噪聲明顯下降。
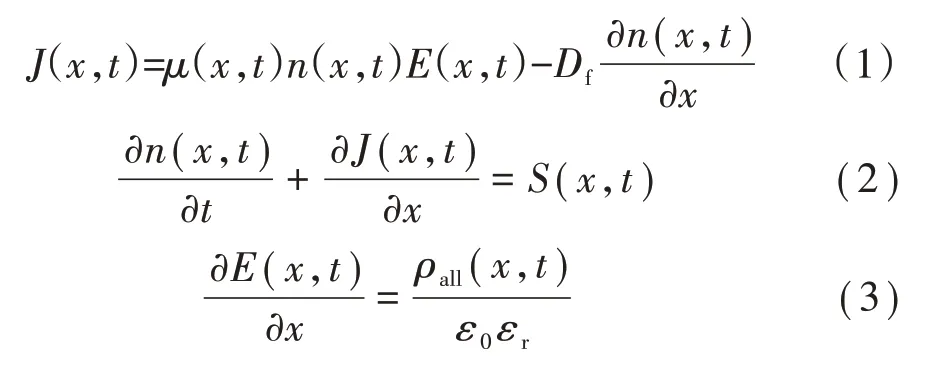
式中:x為位置變量;t為時間變量;J為載流子的通量密度;μ 為載流子的遷移率;n 為載流子密度;E 為電場強度;Df為擴散系數;S 為源項;ρall為總的電荷密度;εr為相對介電常數;ε0為真空介電常數。
使用的載流子遷移率是根據不同場強、不同溫度下的電導測量數據得到的,最終結果與溫度、場強有關,如式(4)所示。
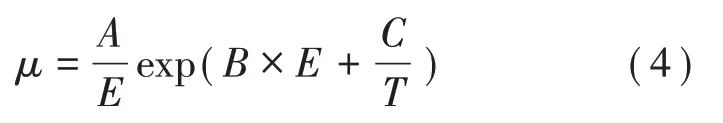
式中:A、B、C為擬合系數;T為溫度。
載流子的注入過程遵循肖特基注入原理,如式(5)和式(6)所示。
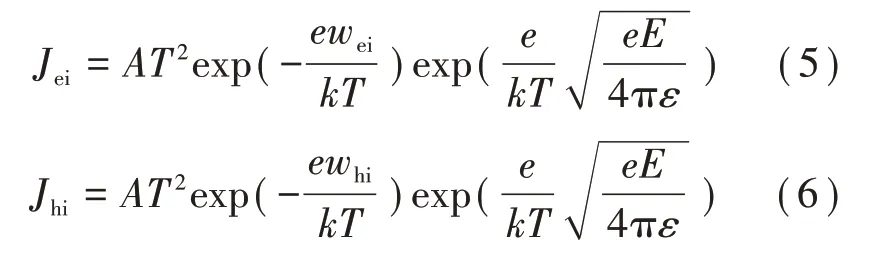
式中:Jhi和Jei分別為在陽極和陰極處注入的通量密度;ωei和ωhi分別為電子和空穴的肖特基注入勢壘;e為電子電量;k為玻爾茲曼常數;ε為介電常數。
對于載流子的抽出過程,采用了認為設置抽出系數的方式,如式(7)和式(8)所示。
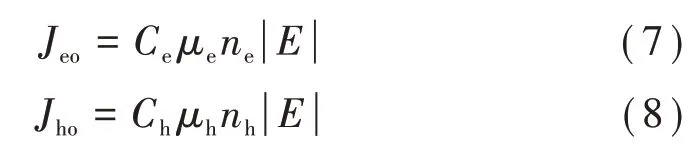
式中:Jho和Jeo分別為空穴在陰極和電子在陽極的抽出通量密度;Ch和Ce分別為空穴和電子在電極處的抽出率,用以近似描述抽出受限;μh和μe分別為空穴遷移率和電子遷移率;nh和ne分別為空穴密度和電子密度。
另外,在電纜的實際運行過程中,由于線芯中電流的作用,線芯的溫度會升高,而電纜的外側由于環境的作用,會保持較低的溫度,這就會在絕緣內外形成一個溫度梯度。在仿真中,溫度梯度的存在也需要納入考慮。
1.2 仿真模型
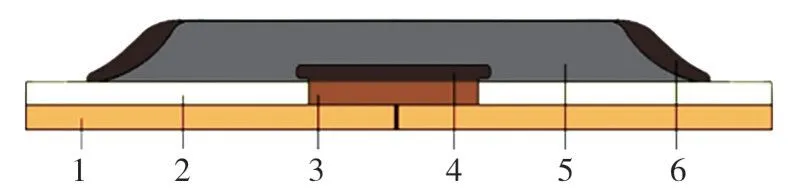
圖2 電纜接頭模型
在本模型中,應力錐和高壓屏蔽均采用半導體材料,而壓接管為金屬材料,而且該中電纜接頭為軸對稱結構,仿真模型可簡化為如圖3 所示的二維軸對稱模型,字母a—h代表電纜接頭上不同的位置。
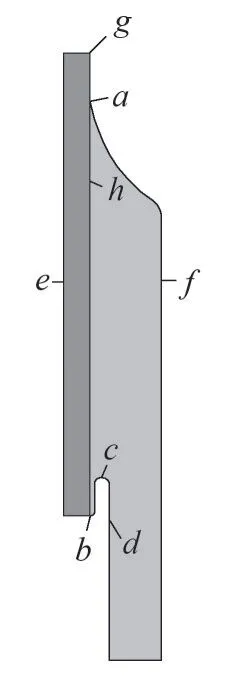
圖3 簡化的電纜接頭模型
表1 為進行空間電荷仿真時使用的部分參數。所采用的電纜接頭外表面溫度為293.15 K,線芯處施加250 kV直流電壓。
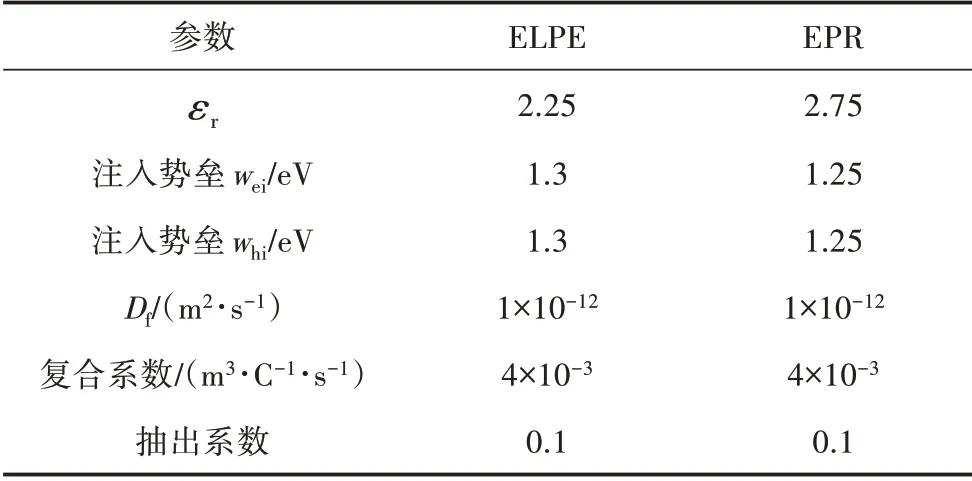
表1 仿真參數
2 結果和討論
2.1 模型驗證
為了驗證前文所述仿真模型的有效性,首先建立了一個簡單的一維模型。利用COMSOL 軟件,根據雙極性載流子輸運模型對一維模型進行了空間電荷仿真,其空間電荷分布如圖4 所示,電場分布結果如圖5所示。
由圖4 可見,在一維模型兩側電極附近,存在異極性空間電荷積聚現象,這是由抽出受限造成的,在異極性電荷積聚的作用下,其電場分布也發生畸變,如圖5 所示,兩端電極處的電場增大,該結果與實驗結果規律相同,說明該模型可以實現空間電荷與電場分布的仿真,是有效的。
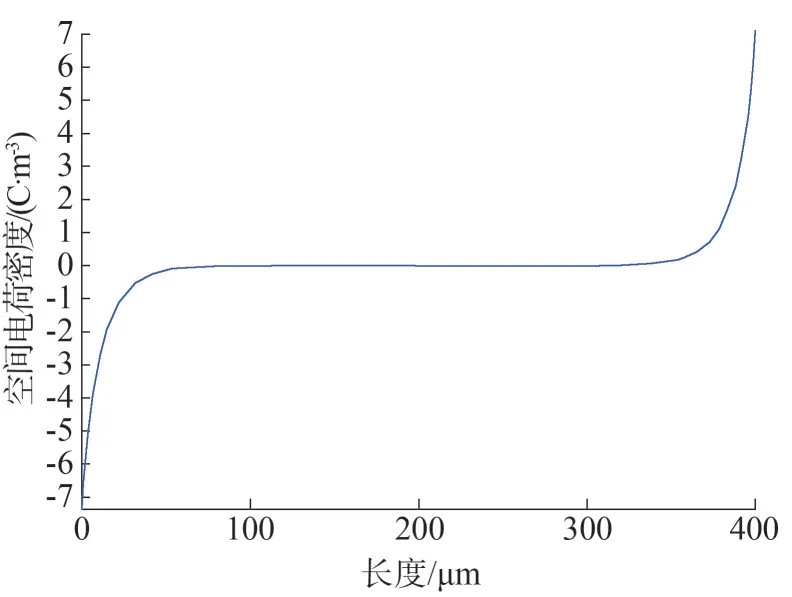
圖4 一維模型中空間電荷分布
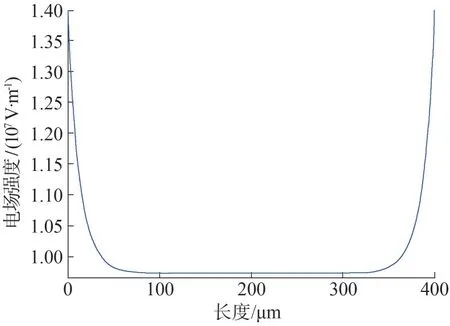
圖5 一維模型中電場分布
2.2 電纜接頭的仿真
使用前文介紹的簡化高壓直流電纜接頭模型,基于雙極性載流子輸運模型,利用COMSOL 仿真軟件,進行高壓直流電纜接頭的空間電荷與電場強度仿真,其電場強度的三維仿真結果如圖6所示。
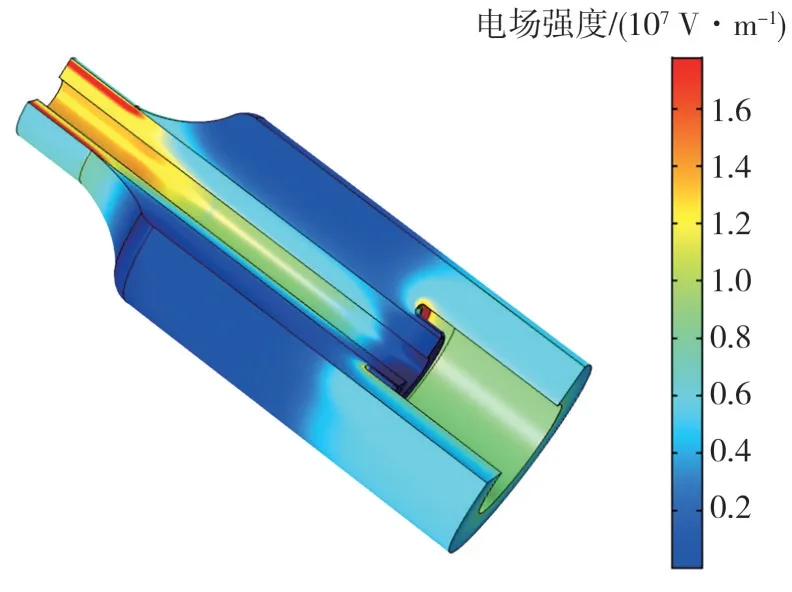
圖6 電纜接頭電場強度三維仿真結果
沿著軸線做截面,其仿真結果如圖7所示。
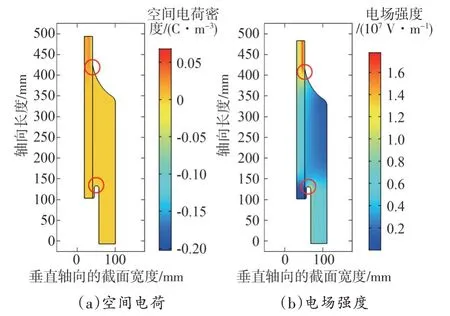
圖7 電纜接頭中空間電荷與電場分布
從圖7 可以看出,在高壓直流電纜接頭的應力錐根部和高壓屏蔽的頂端,出現了嚴重的電場畸變。
為了更加清楚地觀察,對應力錐根部和高壓屏蔽的頂端附近空間電荷和電場強度分布進行了局部放大,如圖8所示。
由圖8 可以看出,在應力錐的根部和高壓屏蔽的頂端,出現了異極性電荷的積聚,從而導致了這兩個部位出現嚴重的電場畸變,成為電纜接頭中的薄弱點。

圖8 應力錐根部和高壓屏蔽的頂端附近空間電荷與電場強度分布
高壓直流電纜接頭中的電場強度最大值出現在高壓屏蔽的頂端,將此處附近(圖3 中b、c、d 連線)的電場強度提取出來,如圖9 所示,可見最大場強達到1.48×107V/m,遠大于3.3×106V/m的平均場強值。
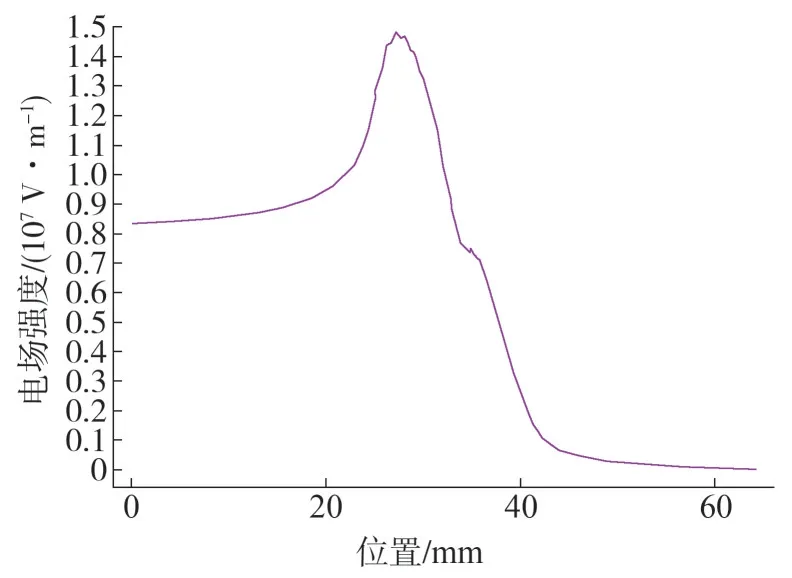
圖9 高壓屏蔽頂端附近電場分布
2.3 界面電荷
電纜接頭中存在兩種不同的絕緣材料,XLPE 和EPR,在兩種材料的界面上,容易出現電荷的積聚現象。
為了觀察電纜接頭中的界面電荷,建立了一條穿過XLPE 和EPR 的截線(圖3 中e—f),這條截線上的空間電荷如圖10所示。
從圖10 中可以看出,在兩種材料的界面處,發生了空間電荷的積聚。這是由于兩種材料的載流子遷移率不同,且兩種材料之間存在勢壘,遷移到此處的電荷不能完全被遷移走,造成了空間電荷的積聚。
2.4 溫度梯度的影響
電纜接頭負荷運行中,線芯發熱使得電纜接頭線芯處與電纜接頭外側存在溫度差,溫度在電纜接頭中呈梯度分布。而溫度的變化將影響電纜接頭中空間電荷的輸運過程[13-15]。
設定電纜接頭外層的溫度恒定為293.15 K。圖11 顯示了內外溫梯為70 K 時,電纜接頭中的溫度分布情況。
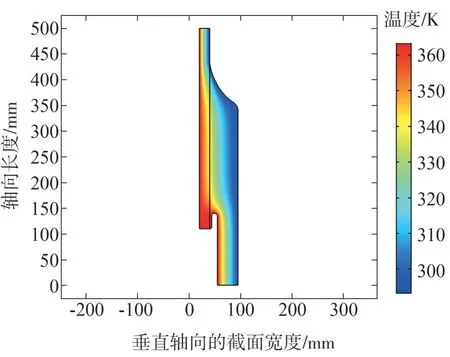
圖11 溫度梯度為70 K時的溫度分布
將高壓屏蔽頂端附近的電場強度分布作為研究對象,其在不同溫度梯度下的電場強度分布如圖12所示。
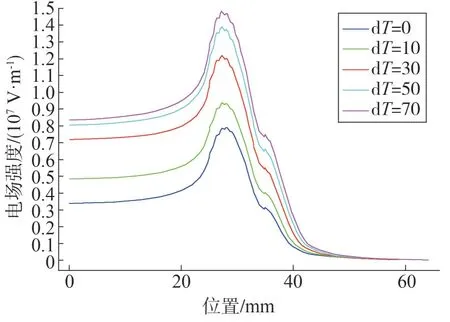
圖12 不同溫梯下高壓屏蔽頂端附近的電場強度分布
由圖12 可以看出,隨著溫度梯度的提高,高壓屏蔽頂端附近的電場強度畸變愈發嚴重。最大值從溫梯為0時的7.9×106V/m增加到了溫梯為70 K時的1.48×107V/m。
若根據按照傳統的電場計算方法,僅考慮電導率而不考慮空間電荷的仿真模型[16],高壓屏蔽頂端附近的電場強度結果如圖13所示。
從圖13可以看出,隨著溫度梯度的增加,該處的電場強度反而減少。這是由于在該模型中,電導率是隨溫度升高而增加的,而高壓屏蔽頂端附近屬于高溫側,溫度升高,電導率增大,此處的場強也相應減少。
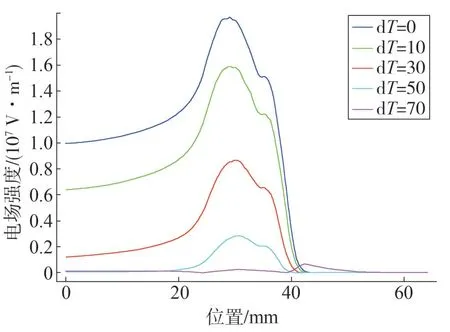
圖13 僅考慮電導時不同溫梯下的電場分布
造成兩種方法之間差異的主要因素,是因為在電導模型中,電荷注入的因素沒有考慮在內。實際情況中,溫度的升高將大大增強電荷的注入,這些電荷的存在將增大電纜接頭中的電場畸變,使用電荷模型更能夠清楚地反映這一過程。
3 結語
基于雙極性載流子輸運模型,利用COMSOL 仿真軟件,構建了高壓直流電纜接頭的仿真模型。根據仿真結果,空間電荷容易累積在應力錐的根部和高壓屏蔽層的末端。高壓直流電纜接頭中的最大電場強度出現在高壓屏蔽層的末端,遠高于平均電場強度。此外,溫度梯度的存在會使電纜接頭中的電場失真更加嚴重。與僅考慮電導率的傳統方法相比,該方法可以準確反映由于載流子注入、抽出和遷移所引起的電場畸變。
仿真方法和結果為高壓直流電纜接頭的設計與優化提供了依據,在設計與制造高壓直流電纜接頭時,應重點關注應力錐的根部和高壓屏蔽的頂端,通過增加曲率半徑、增加過渡非線性材料等方式,降低電場畸變程度。

