封閉邊界壓裂水平井非穩態產能評價新模型

何軍，范子菲，何聰鴿，張安剛，郝峰軍，張新順，劉麗，徐立坤

（中國石油勘探開發研究院，北京 100083）

0 引言

壓裂水平井技術是通過增加井筒與地層的接觸面積，降低流體在地層中的滲流阻力，增加單井控制面積來提高油氣井產能的。該技術已廣泛應用于低滲特低滲、薄層油氣藏及稠油油藏，并使之得以高效開發［1-3］。

準確、快速評價壓裂水平井產能，成為學者們研究的熱點問題之一。任宗孝等［4］在垂直裂縫水平井非穩產產能研究的基礎上，應用Gringarten源函數、坐標轉換及坐標評議原理，建立了傾斜裂縫壓裂水平井產能評價模型，重點分析了裂縫夾角對水平井流動階段、水平井井底壓力的影響。毛新軍等［5］在研究致密油藏壓裂水平井產能時，利用PEBI網格表征水力壓裂過程產生的不同裂縫，通過編制數值模擬程序評價壓裂水平井產能。朱維耀等［6］考慮薄互層儲層砂泥交互、儲層平面均質而縱向非均質的特點，建立了壓裂水平井開發薄互層的穩產滲流數學模型。李波等［7］基于疊加原理、勢函數理論及流體力學相關原理，建立了考慮裂縫污染表皮系數、裂縫非均勻分布的壓裂水平井產能預測模型，并通過正交實驗分析了壓裂水平井產能主控因素，指導壓裂水平井部署及完井優化。牟珍寶等［8］基于水電相似理論，考慮啟動壓力梯度和應力敏感性，利用等值滲流阻力法建立了壓裂水平井產能公式。Rbeawi等［9］建立了傾斜裂縫壓裂水平井滲流模型，分析了裂縫穿透比對壓力動態的影響。曾凡輝等［10-11］將裂縫分解成微元段，利用點源函數理論、積分變化和疊加原理，建立了壓裂水平井半解析產能評價模型。

關于壓裂水平井產能評價方法大多基于穩態滲流，僅反映油氣井的穩態滲流特征。此外，早期滲流模型假設地層為無限大，裂縫為無限導流，這就導致水平井產能預測結果偏大；部分模型考慮了非穩態滲流及裂縫有限導流，但涉及Fredholm型積分的處理，求解復雜，制約了產能評價模型的應用。本文在裂縫等效井徑模型的基礎上，應用鏡像反演及壓降疊加原理建立了封閉邊界壓裂水平井非穩態產能分析新方法，并據此分析各種因素對壓裂水平井產能的影響。本文方法具有求解過程簡單、求解精度高的優點，可以滿足現場壓裂水平井產能預測要求。

1 封閉邊界壓裂水平井產能模型的建立

模型的假設條件：矩形封閉地層，儲層的厚度和滲透率為常數；流體為單相不可壓縮牛頓流體，黏度為常數，滲流滿足達西定律；裂縫為有限導流裂縫，水平井筒為無限導流（水平井筒壓降較小，可以忽略），流體由基質進入裂縫，再由裂縫進入水平井井筒；裂縫形狀為矩形，貫穿整個油層；每條裂縫的參數可以不同，滲流為不穩定滲流。

1.1 裂縫等效井徑

對于裂縫等效井徑，Prats等［12-14］進行了深入的研究。王曉冬等［14］推導了直井有限導流裂縫的等效井徑公式，其計算結果與Prats等的計算結果一致：

式中：rwe為裂縫等效井徑，cm；xf為裂縫半長，cm；UfD為裂縫無因次導流能力；f（ Ufd）為裂縫無因次導流能力影響函數；Kf為裂縫滲透率，μm2；wf為裂縫寬度，cm；K為儲層滲透率，μm2。

水平井裂縫中的流動由兩部分構成——井筒附近的徑向流動和遠離井筒的線性流動。因此，相比直井裂縫中的流動，壓裂水平井裂縫中的流動會在井筒附近產生一個附加壓力降，這種現象稱作徑向聚流效應。Brown等［15］給出了井筒聚流效應的表皮系數：

因此，壓裂水平井裂縫的等效井徑［16］可以表示為

式中：Sc為聚流效應表皮系數；h為儲層厚度，cm；rw為水平井筒井徑，cm。

1.2 鏡像反演

根據式（5），可以將封閉地層壓裂水平井每條裂縫都等效為一口直井（見圖 1，其中 rwe1，rwe2，rwe3，rwe4為相應裂縫的等效井徑）。

矩形地層多口直井的生產可通過鏡像反演轉化為無限大地層多口井的生產（見圖2）。圖2中灰色區域代表原有的封閉地層，這里將圖中灰色區域部分的井定義為裂縫的等效井，其他井為與之對應的鏡像井。虛線矩形部分代表4倍泄流面積，整個地層用虛線矩形均勻剖分，便可得到封閉地層多口直井鏡像反演的結果。在實際計算中，無需進行無窮次反演，只需在縱向和橫向進行有限次反演，便能得到較好的計算結果。

圖2 矩形封閉地層多井鏡像反演

以4條裂縫為例。在虛線矩形上、下、左、右各取n個（n取到一定數值后，就能使計算結果收斂）這樣的矩形，則這樣的矩形個數為 （2n+1）2，總的井數為16×（2n+1）2。通過分析所有井在等效井處的作用，便可求得每口等效井的產量，即壓裂水平井每條裂縫的產量。

在多口井進行壓降疊加的基礎上，無限大地層單井在任意一點產生的壓降的計算公式為

綜上所述，濰北凹陷至少存在兩期油氣充注歷史，沙四段沉積中期至沙河街構造運動開始是該區油氣的主要充注時期。但由于古地溫梯度和埋深不同，導致油氣充注時捕獲的流體溫度存在差異。凹陷東南部的昌70井第一期分布在50～70℃，而北部央5井在90～100℃，說明凹陷東南部烴源灶成熟度相對較低，油氣充注時流體溫度相對較低。同時，部分地區構造運動剝蝕后期沉降量較大，可能存在二次生排烴過程，油氣充注發生在館陶中后期至今，但僅在二次生烴區及其附近存在。此外，早期形成的油氣藏可能在后來的構造運動中破壞發生次生調整形成多期成藏。

式中：pi為原始地層壓力，MPa；x，y分別為地層中任意一點的橫、縱坐標，cm；x0，y0分別為井點對應的橫、縱坐標，cm；p（x，y，t）為地層任意一點壓力，MPa；q 為產量，cm3/s；μ 為流體黏度，mPa·s；η 為導壓系數，cm2/s；t為生產時間，s。

1.3 井點坐標的求取

為了求得每口井的位置坐標，選取圖2中紅色矩形區域為研究單元，并建立相應的坐標系（見圖3）。A1，B1，C1，D1 代表與裂縫 1 相對應的直井；A2，B2，C2，D2 代表與裂縫 2 相對應的直井；A3，B3，C3，D3 代表與裂縫3相對應的直井；A4，B4，C4，D4代表與裂縫4相對應的直井。將虛線矩形區域的16口井展開，就能得到所有井的坐標。

圖3 矩形封閉地層鏡像反演剖分單元

裂縫 i（i=1，2，3，4）的等效井及其鏡像井的 x，y 坐標可以表示為

式中：Wix為裂縫 i（i=1，2，3，4）對應的等效井及鏡像井的 x 坐標構成的矩陣；Wiy為裂縫 i（i=1，2，3，4）對應的等效井及鏡像井的 y 坐標構成的矩陣；Aix，Bix，Cix，Dix分別為代表 Ai，Bi，Ci，Di井及其鏡像井的 x坐標構成的矩陣（該矩陣為（2n+1）（2n+1）的矩陣）；Aiy，Biy，Ciy，Diy分別為代表 Ai，Bi，Ci，Di井及其鏡像井的 y 坐標構成的矩陣（該矩陣為 （2n+1）（2n+1）的矩陣）。

設 A1，A2，A3，A4 井的井點坐標分別為（x1，y1），（x2，y2），（x3，y3），（x4，y4）。為了與 Wix，Wiy的形式保持一致，這里將A1，A2，A3，A4井的井點坐標寫成矩陣的形式。首先令Xi，Yi均為 （2n+1）（2n+1）的矩陣，Xi中每個元素為xi，Yi中每個元素為yi，則等效井的井點坐標可以表示為

式中：Weix為等效井 i（i=1，2，3，4）的 x 坐標構成的矩陣；Weiy為等效井 i（i=1，2，3，4）的 y 坐標構成的矩陣。

rij為等效井 j（j=1，2，3，4）及其鏡像井距等效井 Ai（i=1，2，3，4）距離的平方：

其中： （Wjx-Wejx）2，（Wjy-Wejy）2表示2個矩陣對應元素相減，然后平方；rij為一個 （2n+1 ）×4（ 2n+1）的矩陣，根據下標組合，共有16個這樣的矩陣。

1.4 壓裂水平井產能公式

已經得到了所有井到矩形封閉地層4口等效井之間的距離，接下來應用壓降疊加原理，求每口井在等效井處的壓降：

式中：Δpij為等效井j及其鏡像井在等效井i處產生的壓降，MPa。

當壓裂水平井各條裂縫變產量生產時，此時需要用杜哈美原理求得每個時間步長的壓力降：

式中：Δpij（k）為第k個時間步長下等效井j及其鏡像井在等效井i處產生的壓降，MPa；t（k）為第k個時間步長，s。

為了便于求解每個時間步長的qj，令

式中：fij（k）為在第k個時間步長下等效井j及其鏡像井在等效井i處產生的滲流阻力，MPa·s/cm3。

由于流體在井筒的壓降較小，可以忽略，每口等效井在井底處的壓力是相等的，均為水平井的井底流壓。因此，當只考慮1個時間步長時，針對每口等效直井都有1個壓降方程。以4條裂縫為例，其方程為

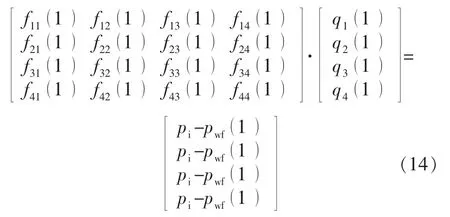
式中：pwf為井底流壓，MPa。

當考慮k個時間步長時，壓裂水平井產能公式為

式中：Fk為在第k個時間步長各條裂縫對應的等效井及其鏡像井分別作用在各個等效井處的滲流阻力構成的矩陣；Qk為第k個時間步長所有等效井產量構成的矩陣；Pk為第k個時間步長所有等效井井底壓降構成的矩陣。

式（16）即為矩形封閉地層4條裂縫壓裂水平井k個時間步長產能求解公式。用相同的方法，可以求出n條裂縫k個時間步長的壓裂水平井產能公式，此時Fk，Qk，Pk分別為

將式（17）代入式（16），即可得到n條裂縫k個時間步長的壓裂水平井產能公式求解通式。

2 實例分析

油藏及壓裂水平井的基本參數為：油藏大小1500m×3 000 m，厚度 10 m，滲透率 0.01 μm2，孔隙度 10%；儲層綜合壓縮系數 5×10-4MPa-1，流體黏度 2 mPa·s；井筒半徑0.1 m，生產壓差10 MPa，水平段長度500 m；裂縫長度100 m，裂縫高度10 m，裂縫寬度1 cm，裂縫滲透率 10 μm2。

2.1 公式精度及可靠性驗證

通過與源函數方法［17］對比，分析本文壓裂水平井產能公式的精度及可靠性。由圖4可知，無論是單裂縫還是3條裂縫壓裂水平井，本文的計算結果與源函數方法的結果都非常接近，二者相對誤差在3%以內，從而證明了本文公式的正確性。

圖4 不同裂縫條數下壓裂水平井產能2種方法計算結果

2.2 壓裂水平井產能與時間的關系

由圖5可知，生產初期壓裂水平井產能變化劇烈，之后趨于平緩。這是由于初期裂縫內液體流動受裂縫間干擾較弱，但隨著生產時間的增長，裂縫間的干擾逐漸增強。隨著裂縫條數的增加，壓裂水平井產能增幅呈減小趨勢。裂縫條數對壓裂水平井產能有較大影響，所以，壓裂設計時應首先考慮裂縫條數對壓裂水平井的增產作用。

圖5 不同裂縫條數下壓裂水平井產能與時間的關系

2.3 壓裂水平井每條裂縫的產能分布

圖6為水平井壓裂5條裂縫生產的情形。由圖可知：首先，裂縫產能初期呈現急劇下降、之后趨于平穩的特征；其次，同一時刻不同裂縫的產能存在差異，表現為外部裂縫產能高、中間裂縫產能低的特征，這是由于外部裂縫受到縫間干擾弱，內部裂縫受到縫間干擾強。

圖6 壓裂水平井裂縫產能分布

2.4 縫長對壓裂水平井產能的影響

由圖7可知，隨著裂縫縫長的增加，水平井產能有所增加，但增加幅度較小。所以，縫長對壓裂水平井產能的影響有限，在壓裂過程中只需保證裂縫縫長在一定范圍即可。

圖7 不同裂縫縫長對水平井產能的影響

2.5 無因次裂縫導流能力對壓裂水平井產能的影響

圖8為無因次裂縫導流能力對壓裂水平井產能的影響。

圖8 不同時間無因次裂縫導流能力對壓裂水平井產能的影響

由圖8可知，無因次裂縫導流能力對壓裂水平井產能具有重要影響。當生產時間較短時（1 d），壓裂水平井產能隨著無因次裂縫導流能力的增大而顯著增加；隨著生產時間的增加（15，30 d），壓裂水平井產能隨無因次裂縫導流能力增加的趨勢逐步減弱。另外，當無因次裂縫導流能力過小（例如0.1）時，壓裂水平井產能急劇下降，因此，要讓水平井具有較高的產能，需使無因次裂縫導流能力大于一定值。

3 結束語

本文在裂縫等效井徑模型的基礎上，應用鏡像反演及壓降疊加原理建立了封閉邊界壓裂水平井非穩態產能分析新方法，據此分析了各種因素對壓裂水平井產能的影響。本文方法求解過程簡單，求解精度高，可以滿足現場壓裂水平井產能預測的要求。