基于CDEM的采空區穩定性及臨界頂板厚度分析

王永增 王心泉 王 潤 馮 春 曹 洋 孟磊磊 吳恩澤

（1.鞍鋼集團礦業有限公司齊大山分公司，遼寧鞍山114000；2.中國科學院力學研究所，北京100190；3.中國科學院大學工程科學學院，北京100049）

地下礦產資源被開采出來后會遺留下采空區，采空區的存在改變了巖體的原有應力場，使得巖體的原有平衡被破壞［1-3］，易產生地表塌陷、地面沉降等問題，對露天開采的安全性存在巨大的威脅［4-6］。采空區頂板的臨界厚度是開采過程安全性評價的重要指標，對采空區穩定性評價有著重要的意義。近年來，不少學者對此進行了深入研究。唐碩等［7］基于模糊物源理論，確定采空區穩定性的影響因素，建立了采空區穩定性評價模型，評價結果用關聯度表示。柳小波等［8］結合第一強度理論提出了頂板厚度計算的新方法，采用Abaqus模擬分析了各因素對采空區頂板破壞的影響規律。姜桂鵬等［9］基于量綱分析法建立了采空區頂板穩定性判別的數學模型，結合有限元數值模擬分析，得到了穩定的臨界厚跨比。唐勝利等［10］基于BP神經網絡原理，結合采空區穩定性影響因素構建了BP神經網絡模型，并對空洞型采空區進行了穩定性評價。王炳文等［11］綜合理論分析和數值模擬結果，對遺留采空區群進行了穩定性級別評定。張瑞等［12］利用三維探測掃描設備建立了采空區三維數值模型，綜合多種采空區穩定性評價方法對采空區進行安全分級。盧欣奇等［13］通過FLAC軟件對近地表采空區進行數值模擬分析，提出了治理方案，并通過FLAC模擬分析對各方案的治理效果進行了對比。張敏思等［14］采用多種理論方法計算了不同跨度采空區頂板的安全厚度，并采用RFPA數值模擬軟件對采空區進行模擬得到頂板出現初始損傷及失穩垮塌的厚度。周平等［15］依據尖點突變模型得到采空區在充填體荷載作用下的頂板厚度表達式。王志修等［16］采用理論計算和數值模擬手段研究了盧安夏露天銅礦地下采空區頂板的安全厚度。胡洪旺等［17］基于Ressiner厚板理論構建了理論分析模型，推導出頂板撓曲線方程及頂板最大應力表達式，并利用Matlab軟件計算得到頂板厚度隨坐標軸變化的三維曲線圖。

現有的采空區頂板穩定性研究理論中，多將采空區頂板視為彈性梁進行近似處理，難以考慮巖石的材料性質對采空區穩定性的影響。同時多數研究只通過數值計算對采空區頂板進行規律性分析，缺少對采空區頂板臨界厚度的定量分析。本研究從量綱分析出發，探討與采空區臨界頂板厚度相關的因素，借助連續-非連續單元法（Continuous-Discontinuous Element Method，CDEM）通過數值分析，找出影響臨界頂板厚度的關鍵變量，得到臨界厚度與相關變量之間對應公式，為評價采空區穩定性提供定量性的參考指標。

1 量綱分析

1.1 采空區臨界頂板厚度影響因素分析

采空區臨界頂板厚度的影響因素復雜，根據以往工程經驗及采空區研究資料，綜合考慮各方面的作用，本研究將影響因素分為幾何形狀因素、地層巖性因素及外力荷載因素［18-19］。

影響采空區臨界頂板厚度Hc的自變量為：①幾何參數為采空區長度a、寬度b和高度h；②材料參數有密度ρ、彈性模量E、泊松比μ、黏聚力c、內摩擦角?、抗拉強度σt和剪脹角ψ；③靜載荷F（假設載荷作用點位于采空區正中）；④重力加速度g（圖1）。

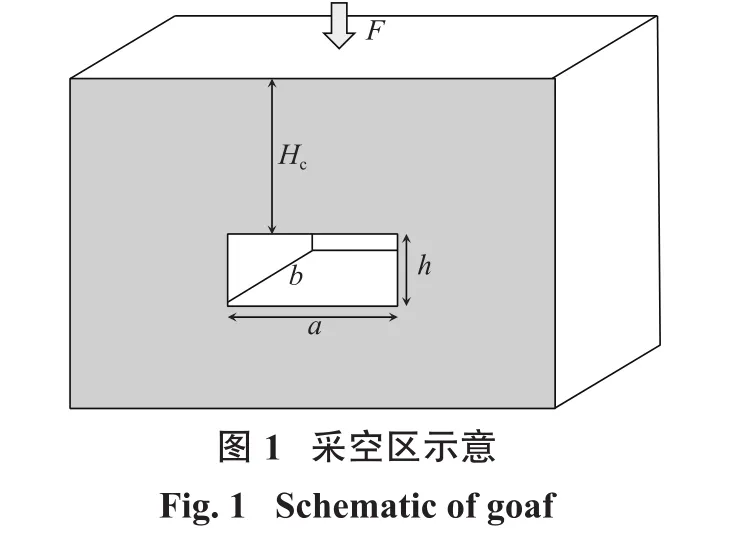
1.2 無量綱表達式建立

臨界頂板厚度Hc與各影響因素之間的關系可表述為

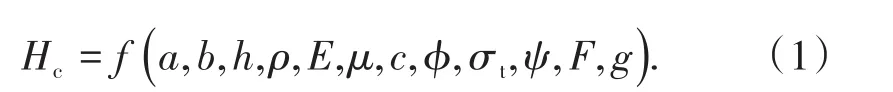
以密度ρ、重力加速度g、采空區長度a為基本量，建立的無量綱表達式為

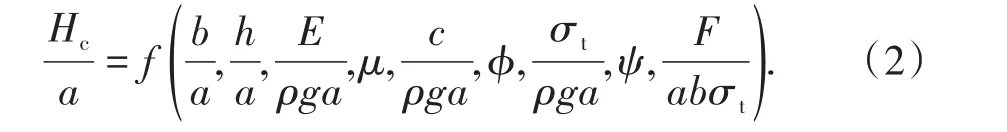
理論分析可知：彈性模量、泊松比對彈性變形有較大的影響，但對臨界頂板厚度Hc影響不大，因此可以忽略；此外，采空區高度h僅對頂板垮落后的下沉距離有影響，對臨界頂板厚度Hc無影響，因此也可以忽略。由此，式（2）可變為

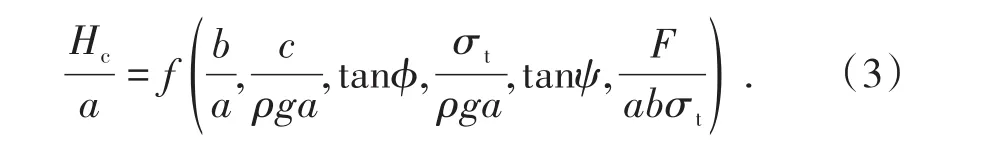
2 采空區穩定性影響因素

2.1 頂板安全系數主要影響因素

本研究采用連續-非連續單元法（CDEM）建立二維采空區數值模型，重點探討采空區的幾何參數及巖體物理力學參數對采空區穩定性的影響規律，并借助安全系數進行定量分析。由于采空區臨界頂板厚度的影響因素眾多，本研究采用多參數分析理論與方法［20-21］對參數進行靈敏度分析，進而給出頂板安全系數的主要影響因素。

計算時根據采空區的常見特征設立一組參數基礎值，當研究某一個參數的影響時，其他參數取基礎值，各參數基礎值取值如表1所示。

根據工程中常見的采空區幾何尺寸及采空區頂板力學參數的取值范圍，確定采空區特征尺寸及采空區頂板力學參數的下限值及上限值。根據以往研究成果，表2中的參數對采空區安全系數的影響都是單調的，故首先研究極限參數下采空區頂板的安全系數，根據安全系數變化值分析參數的敏感性。采空區參數限值及對應的安全系數如表2所示。

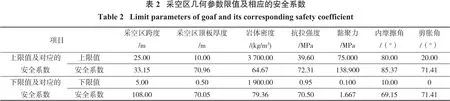
由表2可知：黏聚力對安全系數的影響最大，采空區跨度、巖體內摩擦角、巖體密度次之。因此，本研究重點研究不同頂板厚度下，采空區跨度、黏聚力、內摩擦角、巖體密度與空區頂板安全系數的對應關系。當研究某一參數對頂板穩定性的影響時，剩余參數取值為基礎值。頂板穩定性規律研究時，各影響因素的計算參數取值范圍在設定的基礎值附近，不超過理論及工程上的合理取值范圍，試驗中各參數取值如表3所示。

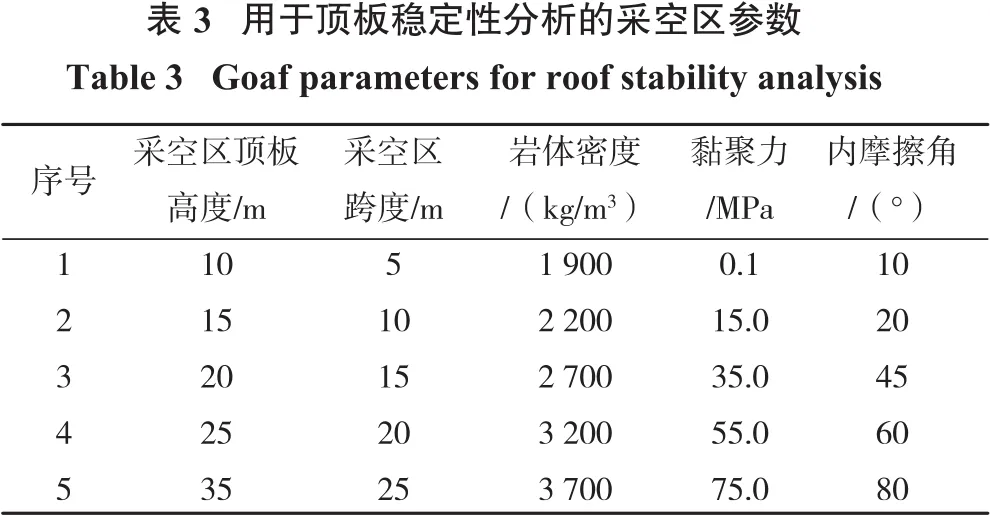
2.2 頂板安全系數變化規律

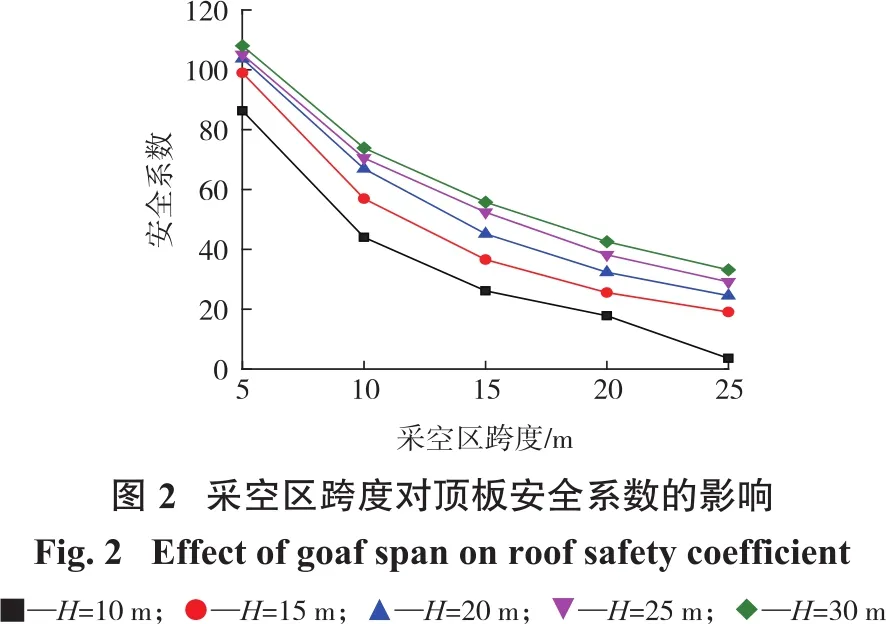
在不同的采空區頂板厚度H下，頂板安全系數與采空區跨度的對應關系如圖2所示。分析該圖可知：隨著采空區跨度增大，安全系數逐漸減小，但減小趨勢逐漸變緩；隨著頂板厚度增大，安全系數逐漸增大，但增大幅度也逐漸變緩。

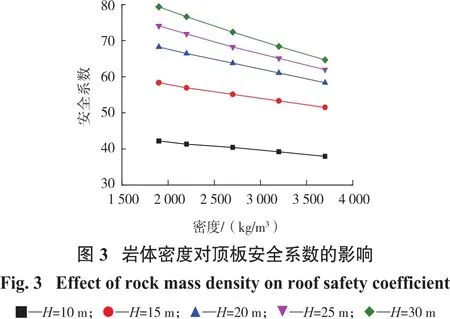
巖體密度對采空區頂板穩定性的影響如圖3所示。由圖3可知：隨著巖體密度增大，頂板安全系數基本呈線性減小趨勢；且隨著頂板厚度增大，安全系數逐漸增大，但增大幅度逐漸變緩。

巖體黏聚力對采空區頂板穩定性的影響規律如圖4所示。由圖4可知：隨著巖體黏聚力增大，頂板安全系數基本呈線性增大趨勢；且隨著頂板厚度增大，安全系數與黏聚力之間直線關系的斜率逐漸增大。

巖體內摩擦角對采空區頂板穩定性的影響規律如圖5所示。由圖5可知：隨著巖體內摩擦角增大，頂板安全系數呈現非線性增大趨勢；內摩擦角小于65°時，基本呈直線變化；大于65°時，安全系數有突然增大現象。總體上，隨著頂板厚度增大，安全系數逐漸增大，但增大趨勢逐漸變緩。

3 采空區臨界頂板厚度分析

本研究借助連續-非連續單元法（CDEM）并采用二維模型及三維模型分別進行采空區臨界頂板厚度分析。二維模型采用連續介質模型進行計算，單元模型為Mohr-Coulomb理想彈塑性本構模型；三維模型采用非連續介質模型進行計算，單元模型為線彈性本構模型，單元間的虛擬界面采用脆性斷裂的Mohr-Coulomb本構模型。

3.1 三維模型下無量綱參數間關系

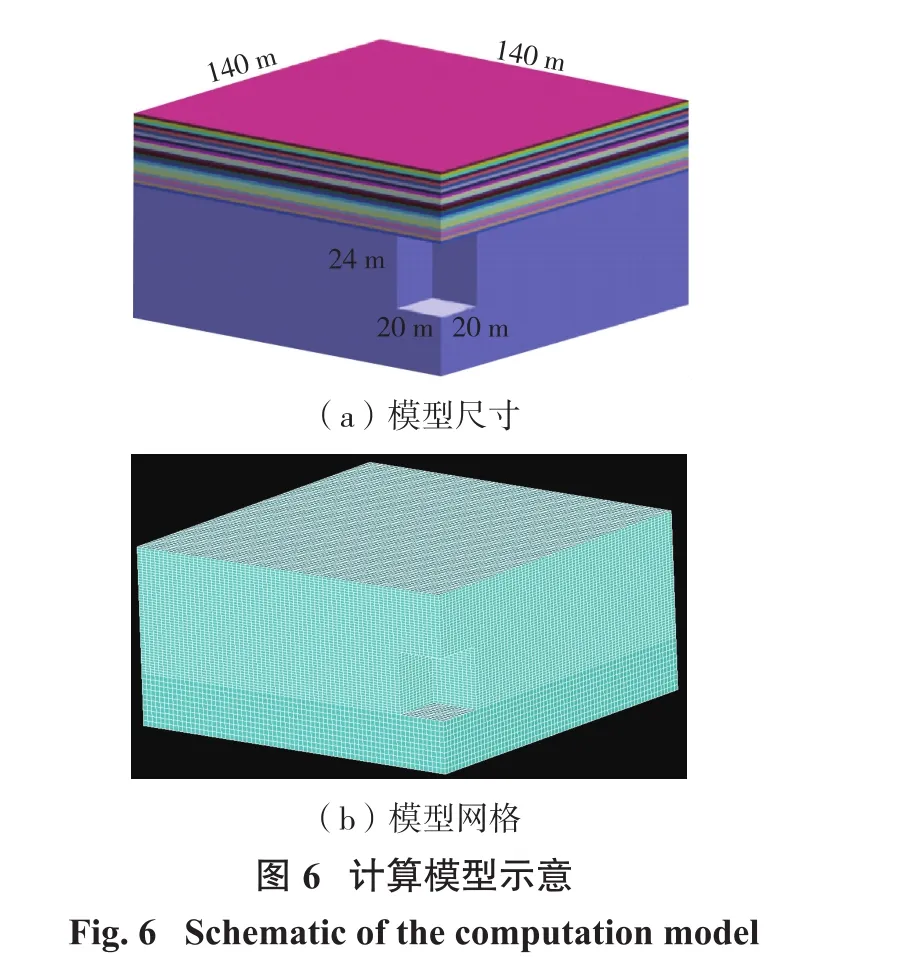
首先探討采空區長度及寬度的影響，建立的三維模型外邊界尺寸為140 m×140 m×64 m（長×寬×高），采空區高度為24 m，本研究假設模型長度a和寬度b一致，如圖6所示。單元模型采用線彈性模型，單元間的邊界采用脆性斷裂模型。計算過程中的基礎參數取值如表1所示。

無量綱臨界厚度與無量綱強度間的關系如圖7所示。由圖7可知：隨著無量綱強度增加，無量綱臨界厚度迅速減小，兩者關系可用下式進行表示：

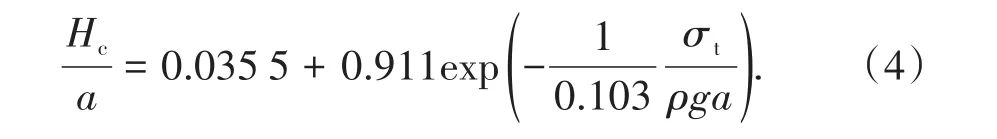
3.2 二維模型下無量綱參數間關系

本研究構建了長100 m、高50 m的二維數值模型，研究無量綱臨界高度與無量綱強度間的對應關系。由于模擬的是二維平面應變問題，因此寬度b為無限大。本研究采用理想彈塑性模型進行分析，計算過程中的基礎參數取值見表1。

共設計3類工況，工況1：設定臨界高度Hc為5 m，采空區高度h為5 m，采空區長度a分別為10、20、30、40、50 m，通過二分法求取對應的強度值；工況2：設定臨界高度Hc為10 m，采空區高度h為5 m，取采空區長度a分別為10、20、30、40、50 m，通過二分法求取相應的強度值；工況3：設定臨界高度Hc為15 m，采空區高度h為5 m，取采空區長度a分別為20、30、40、50 m，通過二分法求取相應的強度值。

第1類工況下，臨界失穩時的塑性體應變云圖如圖8所示。由圖8可知，當Hc/a較大時，采空區頂板主要發生沿著側壁切落；隨著Hc/a減小，采空區頂板側壁易發生拉剪破壞，采空區中部也易發生彎拉 破壞。

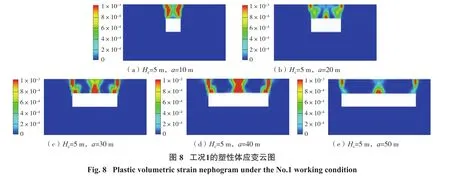
基于上述3種工況的模擬結果，得到了無量綱臨界高度與無量綱強度之間的關系曲線，如圖9所示。由圖9可知：盡管3種工況下，各類參數差異較大，但在無量綱的表述下，均可用一條曲線進行表述，采用指數衰減型函數進行擬合，得到的無量綱臨界高度與無量綱強度的關系式為

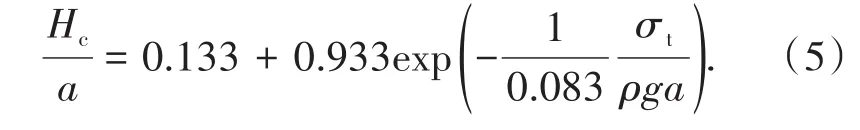
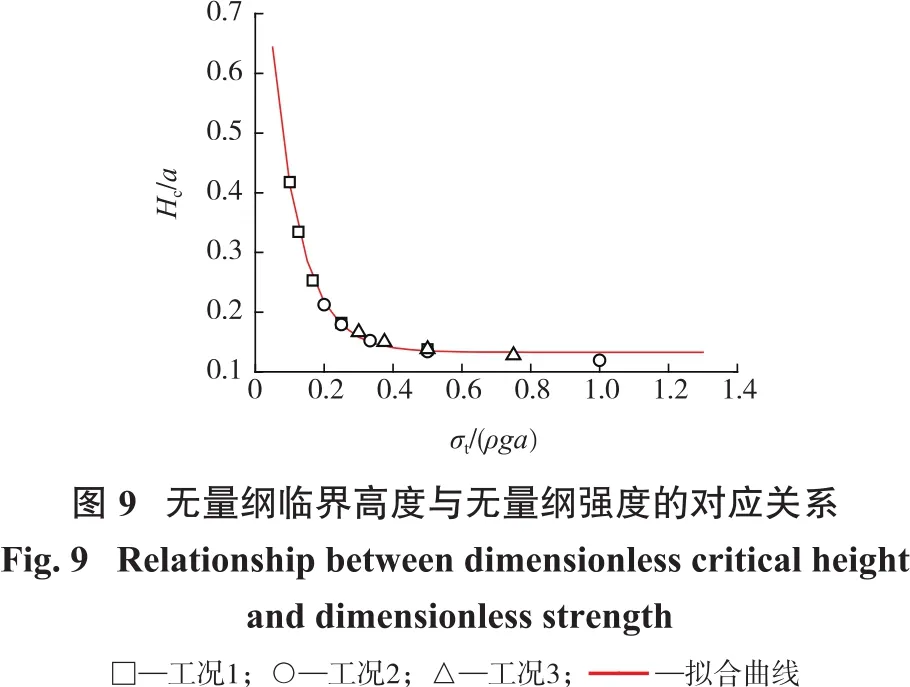
綜合分析式（4）、式（5），可得無量綱高度與無量綱強度之間的關系可表示為

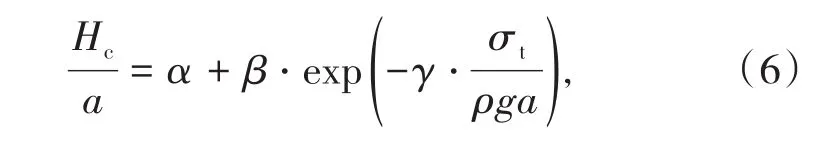
其中，α、β、γ為待定系數。

需要指出的是，式（4）與式（5）的系數有所差別。一方面是由于兩個模型采用了不同的計算模型及計算本構模型；另一方面是由于二維模型忽略了采空區第3個方向尺度對采空區頂板穩定性的影響。

4 結論

（1）借助量綱分析手段，分析了采空區臨界頂板穩定性的主要影響因素，得到與采空區頂板厚度相關的無量綱參數。選取黏聚力、采空區跨度、巖體內摩擦角、巖體密度為參數，借助CDEM數值分析方法，通過改變各參數的取值計算了采空區頂板的安全系數。并對二維、三維兩種模型下無量綱臨界高度與無量綱強度間的對應關系進行了研究，得到了無量綱臨界高度與無量綱強度間的函數表達式。

（2）彈性模量、泊松比對臨界頂板厚度影響不大，采空區高度對臨界頂板厚度無影響；黏聚力對安全系數影響最大，采空區跨度、巖體內摩擦角、巖體密度次之。在只改變某一參數取值的情況下進行分析發現，隨著采空區跨度增加、巖體密度增加、黏聚力減小、內摩擦角減小，頂板安全系數呈減小趨勢；隨著頂板厚度增加，安全系數增加，但增加趨勢變緩；隨著無量綱強度增大，無量綱的臨界頂板高度基本呈指數衰減型的下降趨勢。

（3）在進行二維及三維無量綱臨界高度與無量綱強度關系表達式計算中，由于兩種模型所采用的本構模型有所差別，且二維模型忽略了采空區第3個方向尺度的影響，導致兩種模型雖然關系表達式一致，但在擬合公式的系數取值上存在一定的差異。在下一步工作中，可考慮改變模型本構，或對同一模型改變計算參數，研究表達式系數是否發生變化，再做進一步的研究。