DIRECT算法及其實(shí)現(xiàn)
葛仁磊 王亞男 王毅 張明浩

關(guān)鍵詞: 為了有效地解決傳統(tǒng)Lipschitz函數(shù)極值求解方法向高維推廣時遇到的復(fù)雜度及計(jì)算量急劇增加的問題,DIRECT算法使用超矩形的中心點(diǎn)替代頂點(diǎn),降低了算法的復(fù)雜度及運(yùn)算量。在進(jìn)行初始化后,迭代進(jìn)行“查找潛在超矩形”和“細(xì)分超矩形”,直至運(yùn)算結(jié)果滿足要求。本文從實(shí)用角度出發(fā),對該算法的原理及實(shí)現(xiàn)的細(xì)節(jié)進(jìn)行了全面介紹,并對算法進(jìn)行了實(shí)現(xiàn),驗(yàn)證了算法的可行性。
關(guān)鍵詞: DIRECT算法; 全局優(yōu)化; 細(xì)分超矩形; 潛在超矩形
中圖分類號:TP312? ? ? ? ? 文獻(xiàn)標(biāo)識碼:A? ? 文章編號:1006-8228(2021)05-01-05
DIRECT algorithm and its Python implementation
Ge Renlei, Wang Yanan, Wang Yi, Zhang Minghao
(Offshore Oil Engineering Co., Ltd., Qingdao, Shandong 266500, China)
Abstract: In order to effectively solve the problem that the complexity and calculation increase sharply when the traditional Lipschitz function extremum solving method is extended to high dimension, DIRECT algorithm uses the center point of hyper-rectangles to replace the vertices, which reduces the complexity and calculation of the algorithm. After initialization, iteratively "finding potentially optimal hyper-rectangles" and "subdividing the hyper-rectangles" until the calculation results meet the requirements. In this paper, from the practical point of view, the principle and implementation details of the algorithm are comprehensively introduced, and the algorithm is implemented to verify its feasibility.
Key words: DIRECT algorithm; global optimization; subdividing the hyper-rectangle; potentially optimal hyper-rectangle
0 引言
DIRECT(DIvidingRECTangles,細(xì)分矩形法)算法是屬于Lipschitz函數(shù)在有限區(qū)間內(nèi)極值問題的一種求解方法,其本質(zhì)是一種采樣算法。DIRECT算法不需要求解目標(biāo)函數(shù)的參數(shù),非常適合于黑箱函數(shù)的優(yōu)化仿真[1]。本文拋開DIRECT算法的技術(shù)與理論細(xì)節(jié),展示其具體實(shí)現(xiàn),使得讀者能夠?qū)φ毡疚目焖賹?shí)現(xiàn)應(yīng)用,并在文章最后給出實(shí)際案例以供參考。
1 Lipschitz函數(shù)
函數(shù)[fx]為閉區(qū)間[a,b]上的函數(shù),如果存在正常數(shù)[K]使[fx]滿足:
[fx-fx'≤Kx-x'? ?x,x'∈a,b] ⑴
則稱[fx]為區(qū)間[a,b]上的Lipschitz函數(shù),[K]為Lipschitz常數(shù),所有滿足條件中的[K]中最小的為最佳Lipschitz常數(shù)。一階可導(dǎo)且有界的函數(shù)都是Lipschitz連續(xù)的[2]。根據(jù)定義⑴可得,對任意[x∈a,b]都有:
[ fx≥fa-Kx-a fx≥fb+Kx-b] ⑵
則直線[y=fa-Kx-a]與[y=fb+Kx-b]都位于函數(shù)曲線下方。兩條直線的交點(diǎn)[x1, gK, fa, fb]為函數(shù)[fx]的下界值。
使用相同的方法可以求得在[[a, x1]]和[[x1, b]]兩個區(qū)間內(nèi)下[fx]的下界值。依此類推,區(qū)間的劃分和最小值的求解可以一直迭代下去,直到下界值無限逼近[fx]的最小值。如圖1所示。
2 DIRECT算法
傳統(tǒng)的算法對于一維的Lipschitz函數(shù)最小值的求解問題非常有效,但不便于向n維空間推廣。對一個n維的Lipschitz函數(shù),進(jìn)行一次最小值的迭代就需要對其[2n]個邊界點(diǎn)的函數(shù)值進(jìn)行計(jì)算,效率較低。
DIRECT算法改進(jìn)了此問題。令[x1=m+n/2]并帶入(1)式可得[6]:
[ fx≥fx1+Kx-x1,x≤x1 fx≥fx1-Kx-x1,x≥x1] ⑶
式⑶的幾何意義如圖2步驟(a)所示。后續(xù)對每一個半?yún)^(qū)間使用相同的方法進(jìn)行迭代(圖2步驟(b)),就可以使下界值逐漸逼近[fx]的最小值。
為了便于后文的討論,此處引入以下與DIRECT算法相關(guān)的概念。
超矩形:n維空間內(nèi)的閉區(qū)間。
潛在超矩形:可能存在函數(shù)最小值的超矩形。
細(xì)分超矩形:將超矩形劃分成更小的超矩形的過程。
在不考慮效率的前提下,我們對所有超矩形都進(jìn)行細(xì)分,再計(jì)算細(xì)分區(qū)間的下界值就可以無限逼近函數(shù)的最小值。實(shí)際上只有滿足一定條件的超矩形才是潛在超矩形,在此前提下,我們只需要對潛在超矩形進(jìn)行細(xì)分就能更快的逼近最小值。所以“尋找潛在超矩形”及“細(xì)分超矩形”是DIRECT算法的兩個主要任務(wù)。
2.1 尋找潛在超矩形
假設(shè)[ε]為一較小正常數(shù),[fmin]為當(dāng)前分割下的最優(yōu)解,[ I]為所有超矩形索引的集合,[di]為超矩形中心到超矩形頂點(diǎn)的歐氏距離。如果[j∈I]為潛在矩形,首先根據(jù)[I]內(nèi)元素與[j]的關(guān)系將[I]劃分成三個集合:
[I1=i∈I:di
則[j]滿足以下三個條件[3]:
條件一:
[fcj≤fci, i∈I3] ⑷
條件二:
[max i∈I1fcj-fcidj-di≤min i∈I2fcj-fcidj-di] ⑸
條件三:當(dāng)[fmin≠0]時:
[ε≤fmin-fcifmin+djfminmin i∈I2fci-fcjdi-dj] ⑹
當(dāng)[fmin=0]時:
[fcj≤djmin i∈I2fci-fcjdi-dj] ⑺
[ε]被稱作瓊斯因子(Jones Factor)[8],這個值為經(jīng)驗(yàn)值。實(shí)驗(yàn)證明[1×10-2≤ε≤1×10-7]時對計(jì)算影響不大,[ε]的推薦值為[1×10-4]。以上引理的正確性本文不再論述,如讀者對引理的證明感興趣,可到引文[3]第2.4.3節(jié)中查看詳細(xì)的證明過程。
2.2 細(xì)分超矩形
為了使超矩形在各個維度上的邊長都能不斷減小,保證分割的效率,超矩形的細(xì)分只在一條或多條最長邊上進(jìn)行[4]。圖3、圖4和圖5展示了二維超矩形和三維超矩形的一次分割方法。
2.3 迭代終止條件
在引文[1,2,5,6]中,都使用了當(dāng)?shù)螖?shù)達(dá)到預(yù)設(shè)值T時,結(jié)束該算法。這種方法在規(guī)模特定的問題中得到了很好的應(yīng)用[5-6]。在引文[3]中,對停止迭代條件進(jìn)行了更深入的探討,同時也建議將目標(biāo)函數(shù)的評估次數(shù)及進(jìn)行超矩形分割的深度當(dāng)作終止迭代的條件,這種做法在采樣算法中經(jīng)常用到。
在實(shí)際應(yīng)用中,特別是工程應(yīng)用中函數(shù)的全局區(qū)間最小值[fglobal]往往是未知的。而且正如前文所述,DIRECT算法無法對函數(shù)的參數(shù)及Lipschitz常數(shù)進(jìn)行估計(jì),所以在[fglobal]未知時也無法對[fglobal]進(jìn)行估計(jì)。這導(dǎo)致在實(shí)際應(yīng)用中更常用、更有效的為“精度”或“百分精度”很難作為DIRECT算法的終止條件。
在尋找Lipschitz函數(shù)的最小值過程中,除了獲得函數(shù)最小值外,有時函數(shù)在何處取得最小值對用戶來說也非常重要。用戶自然的會以[fmin]所在超矩形尺寸達(dá)到某一特定要求作為終止迭代的條件[8]。在后面的DIRECT算法實(shí)現(xiàn)中,我們將以[fmin]所在的超矩形最長被細(xì)分的次數(shù)定義為深度,并以深度小于等于給定值作為終止條件之一。
表1總結(jié)了DIRECT算法常用終止條件。
3 性能優(yōu)化
第2節(jié)給定的算法邏輯清晰有效,但效率有待優(yōu)化。本節(jié)從超矩形細(xì)分維度次序、邊長的指數(shù)式存儲和距離的存儲與計(jì)算三個方面討論如何提高DIRECT算法的效率。
3.1 超矩形的細(xì)分維度次序
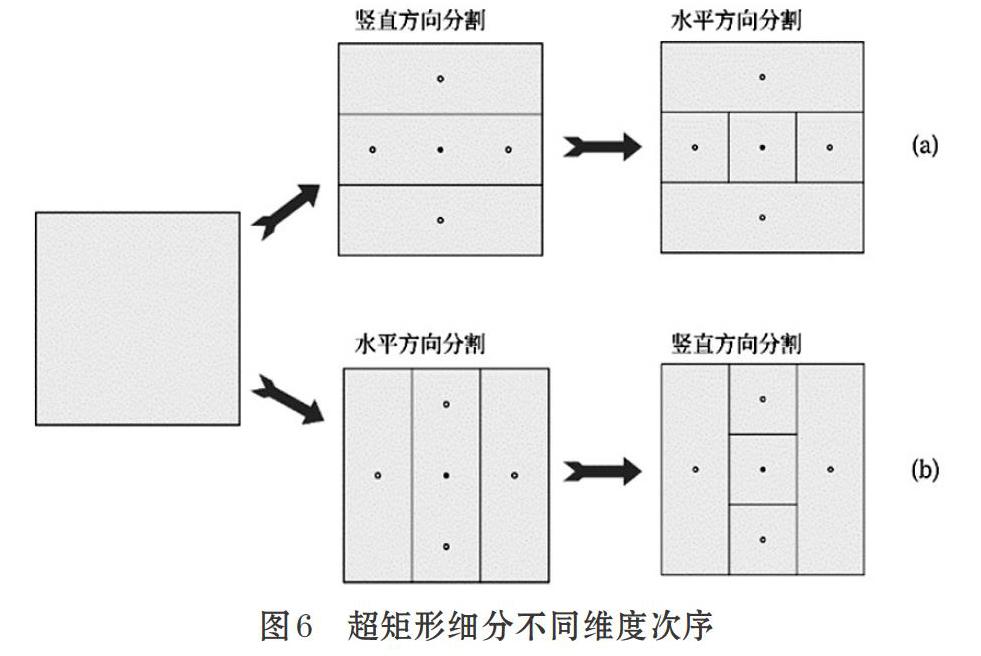
2.2節(jié)中進(jìn)行超矩形的細(xì)分討論時對哪個維度優(yōu)先進(jìn)行細(xì)分并沒有討論。但實(shí)際情況不同維度優(yōu)先會造成不同的效果,如圖6所示。
圖6中(a)與(b)顯示出相同的中心點(diǎn)進(jìn)入了不同尺寸的超矩形中。如在細(xì)分(a)中,左側(cè)中心點(diǎn)最終進(jìn)入了邊長為[13×13]的超矩形中。而在細(xì)分(b)中,該中心點(diǎn)進(jìn)入了邊長為[13×1]超矩形中。這種差別會影響后續(xù)潛在超矩形的查找及下一步分割的工作量。
那么(a)與(b)兩種方式,哪個更有利于后續(xù)運(yùn)算呢?我們使用的策略是將最優(yōu)的函數(shù)值放入到更大的超矩形中,這是由于較大的超矩形總是能夠更快的被再次分割。經(jīng)過實(shí)驗(yàn)也發(fā)現(xiàn),這樣的分割策略的確能夠提高算法速度[6]。
3.2 邊長的指數(shù)式存儲
第2.2節(jié)細(xì)分超矩形的過程(圖2、圖3、圖4)中,每次超矩形的最長邊都會變成原來邊長的[13]。即一條邊如果經(jīng)歷[i]次分割,那么邊的長度會變成原邊長的[3-i]。
為了便于邊長的存儲,在算法開始前將邊長不規(guī)則的初始超矩形映射到所有邊長都為1的超正方形內(nèi)。此后就可以使用指數(shù)[i]來替代原有邊長[3-i]來進(jìn)行存儲、排序等操作,可以節(jié)省空間并提高運(yùn)算效率。
3.3 距離的存儲與計(jì)算
在尋找潛在超矩形時,公式⑸⑹⑺都用到了中心到頂點(diǎn)的距離。DIRECT算法在提出時[6],作者很自然的使用了歐氏距離。歐氏距離是二范數(shù)距離,其計(jì)算涉及平方和開方運(yùn)算,計(jì)算量大,且產(chǎn)生的結(jié)果為實(shí)數(shù)。為了保證計(jì)算精度,往往需要較大的存儲空間。這些原因促使研究者轉(zhuǎn)而研究其他類型的距離是否也能產(chǎn)生相同的效果,以及其他類型的距離能不能加快運(yùn)算速度,節(jié)省存儲空間。
在引文[7]中,作者提出并證明了使用無窮范數(shù)距離可以達(dá)到與歐氏距離相同的效果。超矩形中心到超矩形頂點(diǎn)的無窮范數(shù)距離可以表示為:
[dist∞=3-l/2]
其中[l]表示超矩形最長邊被分割的次數(shù),無窮范數(shù)距離本質(zhì)上就是最長邊的一半。使用無窮范數(shù)距離有如下好處。
⑴ 距離的表示與存儲可以直接使用自然數(shù)[l],減少存儲空間。
⑵ 距離的計(jì)算轉(zhuǎn)化為邊長排序,減少計(jì)算量。
⑶ 在第2.1節(jié)的運(yùn)算中,進(jìn)行條件一運(yùn)算時,能夠得到更少的潛在超矩形,減少后續(xù)查找潛在超矩形的運(yùn)算量。而且會進(jìn)一步減少中心點(diǎn)處函數(shù)值的運(yùn)算次數(shù)。
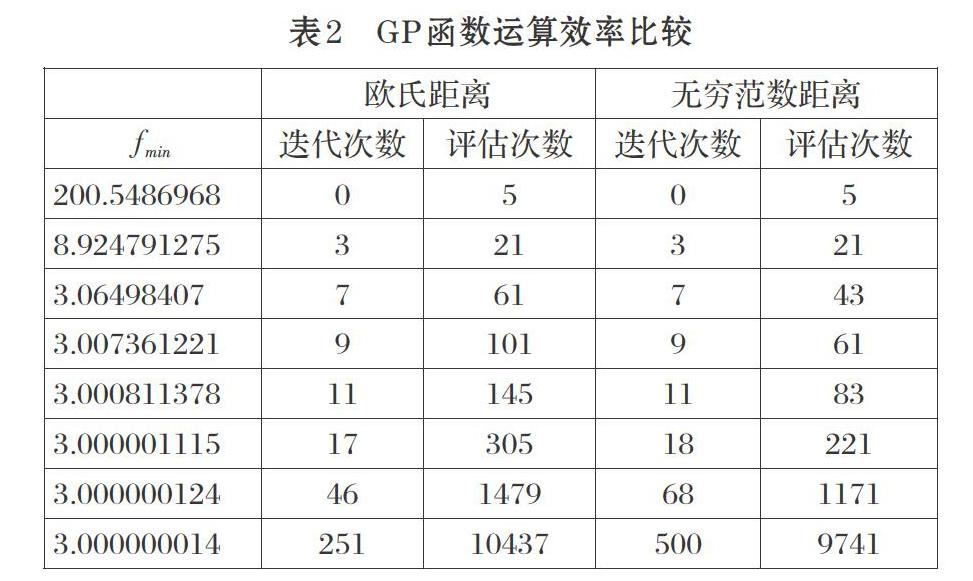
為了比較二范數(shù)與無窮范數(shù)的效率,我們使用GP函數(shù)[8,13]這個例子,分別使用歐氏距離和無窮范數(shù)距離兩種方法進(jìn)行運(yùn)算,得到統(tǒng)計(jì)數(shù)據(jù)如表2所示。
從表2數(shù)據(jù)可以看出,使用無窮范數(shù)作為距離度量時,雖然有時迭代次數(shù)會超過使用二范數(shù)作為距離度量,但在目標(biāo)函數(shù)的計(jì)算次數(shù)上有很大優(yōu)勢。所以本文給出的示例代碼中以無窮范數(shù)作為距離度量。
4 DIRECT算法實(shí)現(xiàn)
4.1 算法流程圖
DIRECT算法總體流程圖7所示。
圖7中步驟a即為第2.2節(jié)“查找潛在超矩形”,其細(xì)節(jié)請參照圖8。步驟b和步驟c合在一起為2.1節(jié)“細(xì)分超矩形”,其細(xì)節(jié)請參照圖9。
4.2 DIRECT算法算例
按照4.1節(jié)提供的流程圖,筆者用Python編寫了DIRECT.py。我們使用引文[4,9]中采用的GoldsteinPrice(GP)測試函數(shù):
[fx=1+x1+x2+1219-14x1+3x21-14x2+6x1x2+3x22]
[×][30+2x1-3x2218-32x1+12x21+48x2-36x1x2+27x22]
同樣,采用與引文[4]相同的范圍[-2≤xi≤2],
[i∈1,2],圖10、圖11表示了在此區(qū)間范圍內(nèi)的圖像:
5 結(jié)束語
DIRECT算法穩(wěn)定性強(qiáng),適用性廣泛,適合在對性能、精度要求不高的情況下使用。本文從實(shí)用角度,全面而詳細(xì)的介紹了DIRECT算法,提供了一種開箱可用的算法,并給出了詳細(xì)的算法流程圖及其實(shí)現(xiàn),讀者可以按照自身需求直接使用。
參考文獻(xiàn)(References):
[1] 安華萍,李文靜.DIRECT優(yōu)化算法計(jì)算機(jī)仿真研究[J].惠州學(xué)院學(xué)報,2019.3:16
[2] Sohrab H H. Basic real analysis[M]. Boston, Basel, Berlin:Birkh?user,2003.
[3] Jones D R, Perttunen C D, Stuckman B E. Lipschitzianoptimization without the Lipschitz constant[J].Journal of optimization Theory and Applications,1993.79(1):157-181
[4] Jorg Maximilian XaverGablonsky. Modifications of thedirect algorithm[M],2001.
[5] Finkel D. DIRECT optimization algorithm user guide[R].North Carolina State University. Center for Research in Scientific Computation,2003.
[6] 宋科康,馮文濤.采用DIRECT算法的外輻射源雷達(dá)高效直接定位方法[J].信號處理,2020.
[7] 王云宏.基于DIRECT算法的微震震源快速網(wǎng)格搜索定位方法研究[J].地球物理學(xué)進(jìn)展,2016.31(4):1700-1708
[8] 武漢大學(xué)測繪學(xué)院測量平差學(xué)科組. 誤差理論與測量平差基礎(chǔ)-第2版[M].武漢大學(xué)出版社,2009.
[9] Cox S E, Haftka R T, Baker C, et al. Globalmultidisciplinary optimization of a high speed civil transport[C]//Proc.Aerospace Numerical Simulation Symposium,1999.99:23-28
[10] Dixon L,Szego G.Towards Global Optimisation 2 North-Holland[J],1978.

