基于圖覆蓋的改進復雜網絡免疫策略

肖詠

摘? 要： 提出一種基于圖覆蓋的改進復雜網絡免疫策略。該方法引入模擬退火的思想，利用局部信息，以節點度大為原則選取免疫節點，同時以一定的概率接受度小的節點。使用交互式郵件傳播模型，在真實的網絡數據集上從免疫效率和免疫代價的角度進行了對比實驗。實驗結果發現，改進的方法在一些社團結構明顯的網絡中具有更好的效果，從而驗證該方法的有效性。

關鍵詞： 圖覆蓋; 免疫策略; 模擬退火; 免疫效率; 免疫代價

中圖分類號：TP391? ? ? ? ? 文獻標識碼：A? ? ?文章編號：1006-8228（2021）05-53-05

An improved complex network immunization strategy based on graph covering

Xiao Yong

（Information Technology Center， Chongqing Medical University， Yuzhong， Chongqing 400016， China）

Abstract： An improved complex network immune strategy based on graph coverage is proposed. This method introduces the idea of simulated annealing， uses local information， selects immune nodes according to the principle of large node degree， and accepts nodes with small degree with a certain probability. Using the interactive e-mail propagation model， a comparative experiment is conducted on real network data sets from the perspective of immune efficiency and immune cost. The experimental results show that the improved method has better effect in some networks with obvious community structure， which verifies the effectiveness of the method.

Key words： graph covering; immune strategy; simulated annealing; immune efficiency; immune cost

0 引言

現今，復雜網絡的病毒傳播相關研究已經成為復雜網絡的重要研究分支，近年來的研究表明，網絡的拓撲結構小世界和無標度特性，在很大程度上影響病毒的傳播行為，在現實復雜網絡中，發生少量病毒感染源即使病毒傳播速率非常低，也可以在網絡中廣泛蔓延開來[1-3]，故挖掘有效的免疫策略來控制病毒的爆發與傳播具有重大現實意義。針對免疫策略，人們做了大量研究，提出了以隨機免疫[4]，目標免疫[5]，熟人免疫[6]，圖覆蓋免疫[7]為代表的一系列免疫策略。本文在圖覆蓋免疫的基礎上，結合模擬退火思想，提出了一種改進的策略。通過在真實社團網絡數據集上的實驗，驗證了本文策略具有更好的免疫效果。

1 復雜網絡免疫策略

復雜網絡一般用圖來表示，一個具體的網絡可抽象為圖G=（V，E），由節點集V（vertex）和邊集E（edge）組成，免疫的核心思想就是想辦法找到一些重要的點，提前采取保護措施來降低節點感染的概率，從而阻止病毒的傳播。

隨機免疫，不考慮節點和網絡拓撲結構的差異，在網絡中隨機選取一定比例的節點進行免疫，發現在均勻網絡中是有效的，而在大規模無標度網絡中幾乎需要免疫所有節點才能控制病毒的傳播，顯然，這是沒有意義的。

目標免疫，其核心思想是找到網絡中一部分重要節點進行免疫，以節點度為代表，這是利用了無標度網絡中大部分節點的度很小、小部分節點的度很大的特性，一旦控制住了度大的節點，其他節點被感染的幾率會顯著降低，花費比較小的代價起到了很好的控制效果。然而作為一個全局性的免疫策略，目標免疫必須遍歷掌握整個網絡的拓撲結構，對于現實大規模和動態網絡，實施難度顯而易見。

熟人免疫，試圖找到一個方法既能克服目標免疫需要全局信息的缺點，又能達到目標免疫的效果，首先在網絡中隨機選取一部分節點，然后以他們為基礎，再次隨機選取他們周圍一個或者多個節點進行免疫，因為無標度網絡大部分節點的度很小，第一次隨機到他們的可能性較大，他們往往連接著度大的節點，第二次隨機到度大的節點概率也較大，故只需要局部信息，就可以獲得比隨機免疫好的效果，但是事實上，這種隨機選擇的方式，在效果上與目標免疫還是有一定的差距。

圖覆蓋免疫在熟人免疫的基礎上加以改進，轉換為一個圖論覆蓋問題，第一次仍然在網絡中隨機選取一部分節點，以他們為中心，再次選取d步以內鄰居中度最大的節點進行免疫，d=1為選取節點的鄰居節點，d=2為選取鄰居的鄰居節點，此方式也是利用了局部信息，第二次有目標的選擇使得它具有比熟人免疫更好的免疫效果。

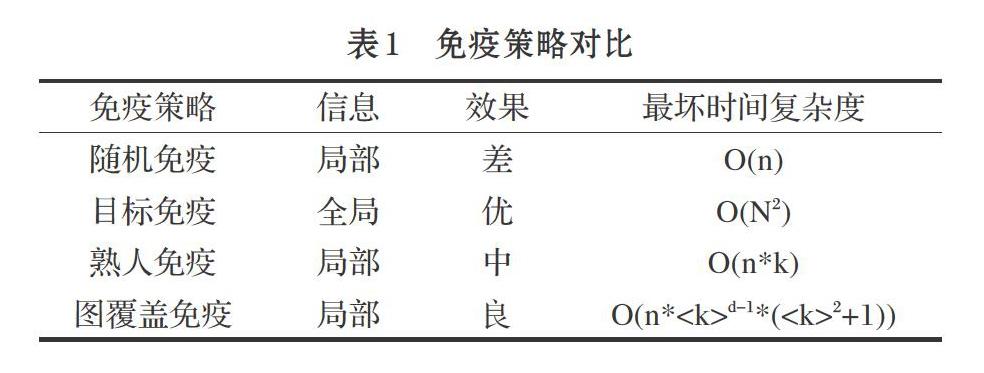
表1為不同免疫策略對比[8]，其中N為節點總數，n為免疫節點數，為平均節點數，k表示策略想要選擇的熟人數目，可以看出，單從免疫效果上講，目標免疫效果最好，但是時間復雜度最高，圖覆蓋免疫效果次之，時間復雜度也相對低些。

2 改進的免疫策略

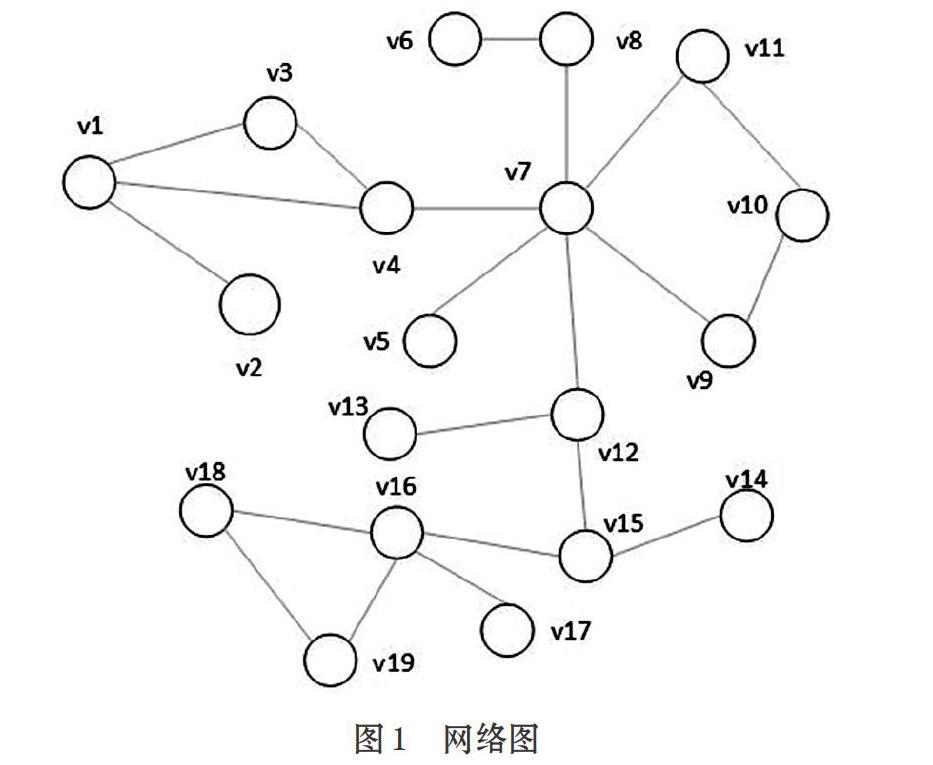
圖覆蓋免疫策略能夠以局部信息獲得較好的免疫效果，在現實網絡中具有較好的操作性，但該策略選擇節點行為固定，受網絡拓撲， 特別是社團結構的影響較大，常陷入局部最優解[8]，以圖1為例，該網絡有明顯的社團結構，假設第一次隨機選擇到種子節點v15，d=1時，根據圖覆蓋免疫的原理，第二次應選擇v16，而我們發現v12盡管不是d=1時的最大度節點，但是它起到更為重要的作為，保護v12能夠阻止病毒朝著v5-v11這個社團傳播，從這個角度看，v16只是局部最優解，從全局看并不能起到最優的效果。

所以圖覆蓋免疫要避免在社團結構明顯的網絡中陷入局部最優解，就不能在第二次選擇過程中只考慮度最大的節點，度小的節點也需要加以考慮，但是也不能直接選擇度小的節點。這里，我們引入模擬退火的思想[9-10]，通過模擬物理中高溫物體的退火過程尋找全局最優解，首先產生一個初始解為當前解，隨著溫度的下降，以一定的概率接受非局部最優解為新解，使之跳出局部最優的陷阱，并重復這個過程至條件結束，開始溫度較高時，接受較差解的概率也比較高，會有更大的機會跳出局部最優解，隨著退火的進行即溫度的逐步下降，算法接收較差解的概率也變小。故我們在第二次選取種子節點的鄰居節點時，不是直接選取度最大的節點，而是以一定的規則去選取，定義選取的規則如下：

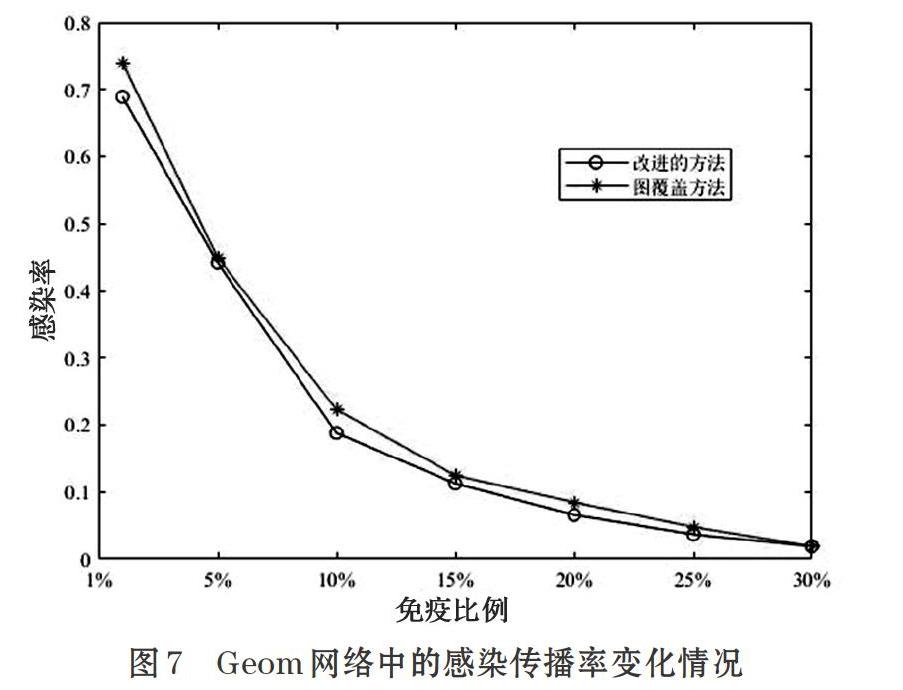
[Pvi=1，? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? vj.deg

其中，T為溫度，vj.deg為在遍歷過程節點過程中臨時解的度，vi.deg為目標節點的度。選取的過程如下。

⑴ 在網絡中第一次隨機選取一部分節點，以它們為中心，假設取d=1，遍歷它們的鄰居節點。

⑵ 初始化溫度T，當前選取節點vj為初始解。

⑶ 如果遍歷到vi，節點vi的度大于vj的度，那么節點vi為新解，否則根據公示計算概率1/（1+exp（（vj.deg-vi.deg）/T）），根據結果決定是否選取節點vi。

⑷ 如果達到終止條件，則算法結束，否則按衰減函數得到新的溫度T重復步驟⑵-⑷。

可以看出，開始溫度較高時，選取度小的概率相對來說還比較高，隨著算法迭代，溫度不斷降低，概率越來越低，并且目標節點的度越小，選取的概率越小，但是不代表一定不選取。為了更好的理解這個過程，我們還是以圖1為例：假設第一次隨機選擇到種子節點v15，d=1，遍歷v15的鄰居節點，v16為初始解，開始設定溫度為100，根據選取規則，選取v14的概率為49.25%，隨著環境變化，假設溫度下降到了10，選取v14的概率為42.56%，盡管概率變小，但還是有跳出局部最優解的可能。

改進后的免疫策略思路為：第一次在網絡中隨機選取一部分節點，以他們為中心，再次在d步以內的鄰居中選取目標節點進行免疫，目標節點以盡量選取度大的為原則，同時以一定的概率接受度小的節點，以跳出局部最優解。

3 實驗分析

3.1 實驗數據集

本文選取NetScience網絡數據集、Geom網絡數據集來進行實驗，NetScience[11]網絡是一些科學家關于網絡原理和實驗研究的合作關系，Geom網絡是科學家關于計算機幾何學研究的合作關系，NetScience網絡和Geom網絡具有明顯的社團結構，表2為它們的基本統計特性。

3.2 實驗方案

盡管免疫的核心問題已經轉化為找出一些重要的節點來進行保護，但評價一種免疫策略的有效性必須結合病毒傳播模型，觀察在病毒的傳播過程中，是否有效地被抑制，本文選擇交互式郵件傳播模型[12]來觀察實驗結果。

在交互式郵件傳播模型中，用戶分為健康、危險、感染三種狀態，病毒的傳播主要與用戶檢查郵件的時間T和點擊病毒郵件的概率C有關，T和C服從高斯分布，本文中T和C的設定與原文模型保持一致，即取T～N（40，202），C～N（0.5，0.32），算法步驟如下。

⑴ 初始化網絡結構。

⑵ 初始化節點狀態，選取感染節點。

⑶ 根據免疫策略選取免疫節點。

⑷ 針對每個節點，用戶查看郵箱操作，如果檢查郵件的時間滿足，并且打開了病毒附件，則被感染，并且向鄰居列表的所有用戶發送病毒郵件，如果沒有打開則默認恢復到健康狀態。

⑸ 更新下次查看郵箱時間。

⑹ 輸出每個時間步的感染節點數。

3.3 實驗結果分析

當病毒在網絡中的傳播趨于相對穩定的狀態時，通過對比被感染的節點數量來衡量免疫策略的效果，為了消除隨機性對實驗結果的影響，我們將對每次實驗運行100次，取100次實驗的平均值作為實驗結果，算法時間步數為600，圖覆蓋半徑d=1，初始隨機感染節點數量為2，圖2、圖3為在2個網絡數據集中取1%（分別為16、73個）的免疫節點后網絡中被感染的節點數量隨時間的變化趨勢，實驗結果表明，病毒攻擊網絡后，網絡中被感染的節點快速上升，隨著時間的增加，慢慢趨于平衡，對比原方法和本文改進的方法，采用本文改進的方法最終被感染的節點低于原方法，效果有所提升，在2個網絡中分別提升約13%和7%。同時我們發現由于實驗結果無法避免隨機性，本文的方法也存在無法優于原方法的情形，出現這種情形是由于不是每次實驗都會陷入局部最優解。

圖4、圖5為在不同免疫比例下被感染的節點數量，在同一免疫比例下，本文改進的方法效果優于原方法，隨著免疫比例的提升，網絡中被感染的節點數量明顯下降，病毒的傳播被控制在比較低的水平。

考慮免疫效率的同時，免疫代價也不可忽視，它也是衡量免疫策略有效性的一個重要指標，即采用較少的免疫節點使病毒感染傳播率達到一個較低的水平，病毒感染傳播率ρ=ρf/ρ0，ρf為采用免疫策略后的感染密度，ρ0為沒有采用免疫策略的感染密度，感染密度為感染節點數與總節點數的比值，定義?c作為免疫臨界值，表示當病毒的感染傳播率ρ趨于0時，所需要的免疫節點比例值。本文對此設計了另一組實驗，圖6、圖7的實驗結果為網絡中病毒感染傳播率隨免疫比例的變化情況，結果表明為了使病毒的感染傳播率控制在一定比例下，在趨近免疫臨界值時，本文改進的方法能夠使用更小的免疫節點比例值，以較小的免疫代價有效地保護網絡，控制病毒的傳播。

4 結束語

復雜網絡的免疫策略研究對抑制病毒傳播具有重點現實意義，本文先對比分析了幾種經典的免疫策略，基于圖覆蓋免疫策略，引入模擬退火的思想，提出一種改進方法，結合交互式郵件傳播模型，在真實的網絡數據上設計了多組實驗，從免疫效率和免疫代價的角度對比了原方法和本文改進的方法，發現改進的方法在一些社團結構明顯的網絡中具有更好的效果，從而驗證了本文方法的有效性。未來的研究方向是針對不同的網絡，如何選取圖覆蓋距離d的取值。

參考文獻（References）：

[1] 阮中遠.復雜網絡上的流行病傳播[J].中國科學：物理學力學天文學，2020.1.

[2] 葛新，趙海，張君.基于熟人免疫的復雜網絡免疫策略[J].計算機科學，2011.38（11）：83-86

[3] 李向華，王欣，高超.復雜網絡免疫策略分析[J].吉林大學學報（理學版），2013.3：444-452

[4] Cohen J E. Infectious Diseases of Humans： Dynamics andControl[J].JAMA The Journal of the American Medical Association，1992.268（23）：3381

[5] Pastor-Satorras R， Vespignani A. Immunization ofcomplex networks.[J].Physical Review E，2002.65（3）：106-126

[6] Cohen R， Havlin S， Ben-Avraham D. Efficient Immuniza-tion Strategies for Computer Networksand Populations[J].Phys Rev Lett，2003.91（24）12343-12343

[7] P E， J G， Y M， et al. Distance-d covering problems inscale-free networks with degreecorrelations[J].Physical Review E，2005.71（3）：142-154

[8] Gao C，Liu J， Zhong N.Network Immunization withDistributed Autonomy-Oriented Entities[J]. IEEE Transactions on Parallel & Distributed Systems，2011.22（7）：1222-1229

[9] Metropolis N ， Rosenbluth A W ， Rosenbluth M N， et al.Equation of State Calculations by Fast Computing Machines[J].The Journal of Chemical Physics，2004.21.

[10] Jinna Ma， Yong Xiao， Hailing Xiong. An Improved AOC-Based Immunization Strategy Based on Simulated Annealing[J]. Journal of Computational Information Systems，2015.11（8）： 2915-292

[11] Newman M E. Finding community structure in networksusing the eigenvectors of matrices[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics，2006.74（3 Pt 2）：92-100

[12] Zou C C， Towsley D， Gong W. Modeling and SimulationStudy of the Propagation and Defense of Internet Email Worm[J]. IEEE Transactions on Dependable and Secure Computing，2007.