魯棒自加權的多視圖子空間聚類

范瑞東，侯臣平

國防科技大學 文理學院 體系科學系，長沙410073

+通信作者E-mail:hcpnudt@hotmail.com

在大數據時代，人們搜集、傳遞和存儲數據的能力不斷提高，各個領域都已經積累了大量的數據。并且其中的大部分數據呈現多源、多態和異構等特性。在許多圖像處理和模式識別的應用中，數據從不同的領域收集或者用不同的特征提取器獲得。比如：用不同的語種來描述同一對象；從不同的角度去分析同一件事；由不同的報社報道同一條新聞等。像這類從不同的途徑或者視角來形容同一目標的數據稱為多視圖數據。

然而，并不是所有的數據都具有標簽的。以圖像數據的獲取為例，由于大部分網絡圖像是由用戶提供的，而為這些數據打標簽需要人工操作，會產生昂貴的勞動成本；并且對于某些復雜的圖像來說，人工標注十分困難。因此，在真實數據集中，無標簽數據占據了絕大部分。從而，為了充分利用這些無標簽多視圖數據，聚類算法受到越來越多的關注。

在過去的幾十年里，人們研究了許多先進的聚類算法。雖然這些聚類算法在一定程度上是非常有效的，但它們大多只適用于單視圖數據。即使將所有視圖連接到一個單獨的視圖中，然后在這個單獨的視圖上采用最先進的聚類算法也可能不會提高聚類性能，因為每個視圖都是對應著異構特征空間中的特定特征，不同的視圖包含著相互獨立和相互補充的信息。因此，多視圖聚類算法（multi-view clustering，MVC）應運而生。多視圖聚類算法考慮了不同視圖的多樣性和互補性，可以更有效地處理多視圖數據，從而提高聚類效果。

現階段的多視圖聚類算法有很多，根據這些算法所依據的機制和原則，將它們分為以下四類：多視圖協同訓練算法[1-2]、多視圖多核學習算法[3-4]、多視圖圖學習聚類算法[5-6]和多視圖子空間聚類算法[7-10]。本文主要關注其中的多視圖子空間聚類算法，這類算法基于所有視圖共享一個表示的假設，旨在從所有視圖中學習一個統一的特征表示。典型的方法是矩陣分解（matrix factorization，MF）。

基于矩陣分解的多視圖子空間聚類算法有很多，本文簡單介紹其中幾種經典的方法。文獻[11]提出一種基于聯合非負矩陣分解的多視圖算法，這是首次將非負矩陣分解應用到多視圖聚類之中。考慮到數據間的內部相關性，文獻[12]通過構造近鄰圖矩陣來整合各視圖局部幾何信息，提出一種帶局部圖正則化的多視圖非負矩陣分解算法。考慮到多視圖數據的同質因子與異質因子，文獻[13]提出一種基于非負矩陣分解的綜合多視圖聚類算法。為了提取所有視圖共享的公共組件和特定于每個視圖的單個組件，文獻[14]提出了簇成分分析這一多視圖聚類算法。文獻[15]提出稀疏多視圖矩陣分解算法，旨在根據方差的視圖特異性對特性進行優先級排序。為了提高多視圖表示的多樣性，減少多視圖表示之間的冗余，文獻[16]提出多視圖表示的多元非負矩陣分解算法。

雖然傳統的基于矩陣分解的多視圖子空間聚類算法在許多場景下取得了優異的效果，但是仍然存在一些不足之處。（1）魯棒數據在真實數據集中存在并且影響著模型性能[17]。大部分基于矩陣分解的算法認為數據點具有平方殘差，很少有考慮到誤差較大的離群點對算法的影響。（2）大部分傳統的基于矩陣分解的多視圖聚類算法認為不同的視圖在模型中會產生不同的影響，通過引入額外的超參數來解決該問題，但是模型的復雜度會提高。

為了解決上述問題，本文提出一種魯棒自加權的多視圖子空間聚類模型（robust auto-weighted multiview subspace clustering，RASC）。本文將數據矩陣分為稀疏誤差矩陣和低秩數據矩陣，而低秩數據矩陣可以通過矩陣分解來獲得多視圖共有表示。在稀疏誤差矩陣上加入?1范數來減少誤差較大的離群點對結果的影響，并且在目標函數的矩陣分解項中用Frobenius范數來代替平方范數，自動學習了各個視圖的權重。本文提出了一個有效的算法來解決RASC中的優化問題，并且為RASC 的收斂性提供了詳細的證明。相比于傳統的多視圖子空間聚類算法，RASC在某些數據集上表現出優異的性能。

1 相關算法介紹

本章詳細介紹四種經典的多視圖聚類算法：具有結構稀疏性的潛在分解空間學習（factorized latent spaces with structured sparsity，FLS）[18]、基于聯合非負矩陣分解的多視圖聚類（multi-view clustering via joint non-negative matrix factorization，MultiNMF）[11]、帶圖正則化的多視圖非負矩陣分解（graph regularized multiview non-negative matrix factorization，EquiNMF）[19]和無參數自加權圖學習（parameter free auto-weighted multiple graph learning，AMGL）[20]。其中，FLS、MultiNMF和EquiNMF 是基于矩陣分解的算法，AMGL 是基于自加權圖學習的算法。

1.1 FLS

FLS 是一個通用的框架，許多經典的特征提取方法可以看作FLS 的特殊情況。具體來說，FLS 框架將一個d×c維的數據矩陣X分解為d×r維的矩陣D與r×c維的矩陣A的乘積，并且使得由矩陣分解產生的誤差盡可能得小。此外，FLS 利用正則化項來約束矩陣D與矩陣A的形式。因此FLS 可以表述為以下模型：

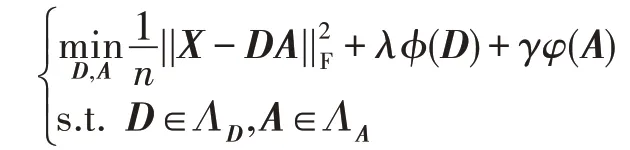
其中，ΛD、ΛA分別是權重矩陣D與潛在表示矩陣A所對應的定義域。這兩個定義域對應著模型能夠對D與A增加額外約束。許多現有的特征提取算法可以看作FLS 的特殊情況，如表1 所示。

Table 1 Special cases of FLS表1 FLS 的特殊情況

1.2 MultiNMF

MultiNMF 是一種通過非負矩陣分解求得多視圖共有表示的多視圖聚類算法。具體來說，相比于FLS 直接在各個視圖上獲得共有表示，MultiNMF 設計了一個帶約束的聯合矩陣分解，即通過增加約束項將各個視圖的低維表示推向一個共有表示。模型如下：

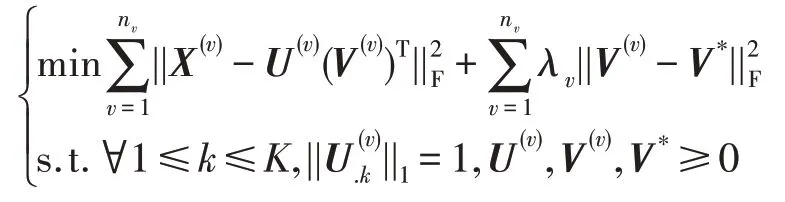
其中，V(v)是在單個視圖上學得的低維表示，V*是學得的共有表示。λv相當于視圖的權重系數。

1.3 EquiNMF

EquiNMF 是一種基于圖學習和非負矩陣分解的多視圖聚類方法。具體來說，EquiNMF 在FLS 框架的基礎上加入了圖正則化項，而且假設每個視圖的貢獻相同并且圖正則化項和所有視圖對目標函數的影響相同，從而EquiNMF 是一個無參數算法，其模型如下所示：

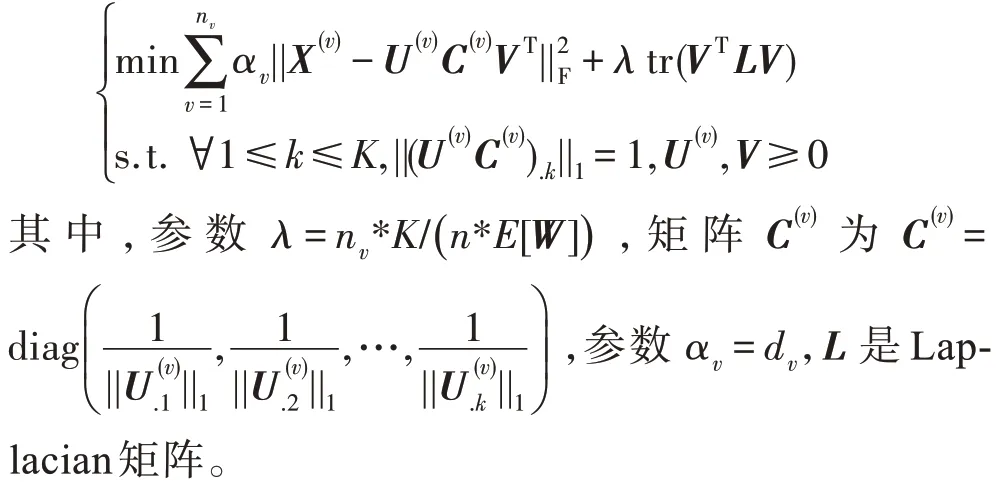
1.4 AMGL

AMGL 是一個既可以用于多視圖聚類，又可以用于半監督分類的無參數圖學習框架。本文的目標是解決一個無監督的問題，因此只關心AMGL 中的多視圖聚類部分，其模型如下所示：

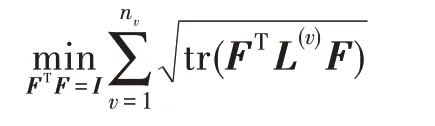
其中，L(v)是歸一化后的Laplacian 矩陣。

2 魯棒自加權的多視圖子空間聚類算法

本章首先介紹一些基本符號的含義，在此基礎上提出本文的模型，并給出該模型的求解算法。

2.1 基本定義

本文將文中常用符號的定義總結在表2 中。Frobenius范數的符號為||·||F，?1范數的符號為||·||1。

2.2 RASC 算法

假設現在有nv個視圖，X=[X(1),X(2),…,X(nv)]T表示所有視圖的數據。由之前介紹的FLS 模型可以得到多視圖的矩陣分解框架為：

Table 2 Common symbols and their definitions表2 常用符號及其定義

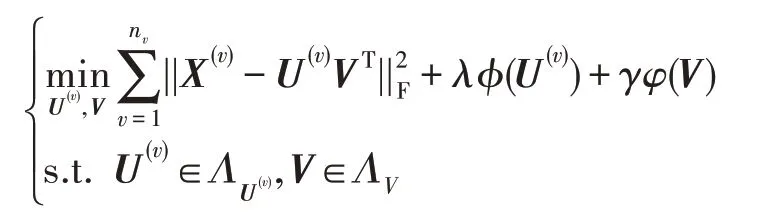
普通的多視圖子空間聚類算法盡管可以取得很好的效果，但是現實生活中的很多數據是有誤差的，很少情況下數據直接具有低秩的性質，因此直接在數據上做矩陣分解是不夠合理的。盡管可以將約束條件X(v)=U(v)VT放縮到目標函數中變為，但是通過放縮后的模型只能處理小誤差的情況，當面對數據有誤差較大的離群點時，很難只通過矩陣分解做到對數據的有效擬合。現有的基于矩陣分解的多視圖算法絕大多數都是直接擬合數據矩陣而忽視了離群點對模型的影響。基于這種思考，假設數據矩陣X是由稀疏誤差矩陣E與低秩數據矩陣M組成，即：

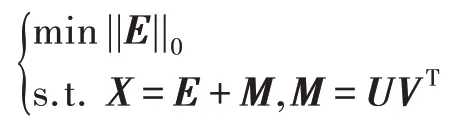
將上述思想應用到多視圖中，則魯棒多視圖子空間聚類模型為：

從理論上來講，?0范數具有理想稀疏性，應該為首選稀疏范數。但是該問題為NP-Hard 問題，在實際求解中很難直接應用。在壓縮感知文獻中得知,在基于測量矩陣具有有限等距性質的條件下，經?1范數松弛后的問題的解近似于?0范數原問題的解，而且經?1范數松弛后的問題為一個凸問題。因此在本文中用?1范數松弛?0范數，模型如下：

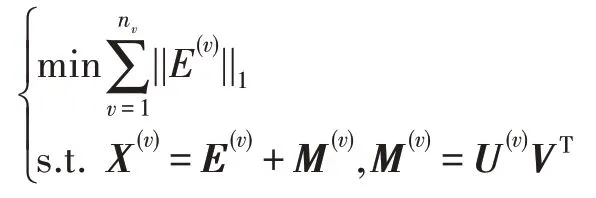
為了排除數據具有小誤差對問題的影響，決定將條件M(v)=U(v)VT以上面放縮的形式進行處理。受到AMGL 模型的啟發，本文直接以Frobenius 范數作為該條件的形式，這種放縮形式本質上是起到了對各個視圖加權的效果。

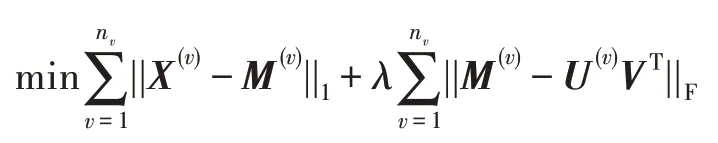
其中，λ是平衡目標函數前后兩項的系數，即平衡數據大誤差和小誤差對模型影響關鍵參數。

最后，需要考慮自由度的問題：即對于任意可逆的矩陣G，滿足。即對于任何最優解，有無窮多個等價的最優解與其對應。因此為了降低目標函數的自由度，并且為之后評價聚類效果做準備，在該模型中加入約束VTV=I，則最終本文的RASC 模型如下所示：

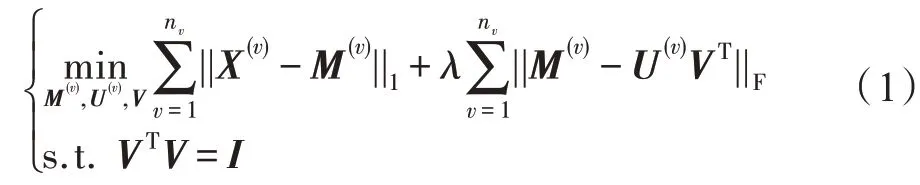
2.3 模型求解

本節將詳細介紹RASC 模型的求解過程。由式（1）可以得到RASC 模型有三組變量需要求解。其中M(v)為數據矩陣X(v)的低秩近似矩陣，U(v)為近似矩陣M(v)的低維投影矩陣，V為所有視圖的近似矩陣M(v)所共有的低維表示。但是由于這三組變量耦合在模型的第二項中，很難直接對模型進行求解。因此采用交替最小化方法（alternating minimization，AM）來求解本模型，即交替固定兩組變量，只優化剩余一組變量。

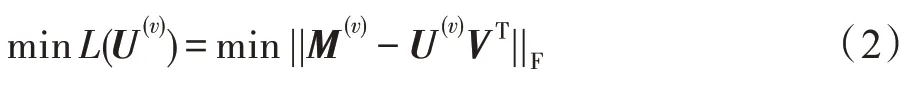
對于U(v)來說，這個問題是一個凸問題，因此令其導數為0 的U(v)即為最優解。

可以發現α(v)的取值依賴于近似矩陣M(v)，很難直接求解式（6）。如果將α(v)取為固定值，則式（5）變為：

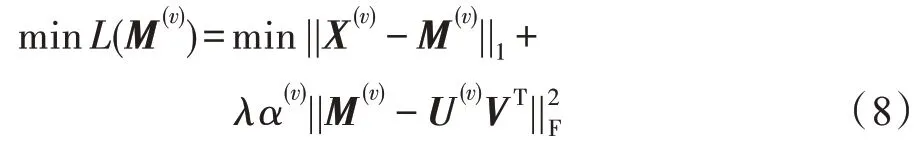
式（8）很容易求出它的最優解。因此可以先由式（8）求出近似矩陣M(v)，再通過式（7）求出α(v)，即通過迭代策略求解問題（5）。

現在給出式（8）的求解過程；由于該問題含有?1范數，直接對該目標函數求導很難得到最優解，故分三種情況進行討論：

假設W的奇異值分解（singular value decomposition，SVD）形式為W=AΔBT，其中，A∈RK×K，Δ∈RK×K，BT∈RK×n。然后可以得到：

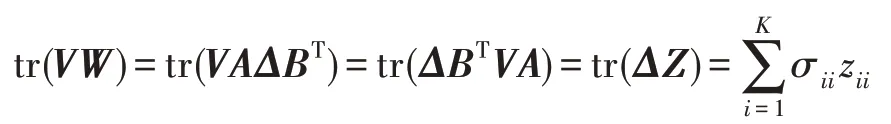
其中，Z=BTVA∈RK×K，σii、zii為矩陣Δ、Z對應的第(i,i)個元素。又VTV=I，則|zii|≤1，從而：

等式成立當且僅當zii=1。又BTB=I，ATA=I，則該問題的最優解為：

基于上述模型分量求解過程，本文的魯棒自加權的多視圖子空間聚類算法的詳細求解步驟如算法1所示。

算法1魯棒自加權的多視圖子空間聚類算法

輸入：多視圖數據X=[X(1),X(2),…,X(nv)]T，聚類數K，參數λ。

輸出：共有表示矩陣V。

1.初始化：近似矩陣M(v)=X(v)，共有表示V=V0。

反復迭代以下步驟：

3.根據式（7）更新自權重系數α(v)；

4.根據式（13）更新近似矩陣M(v)；

5.根據式（17）更新共有表示V；

直至滿足收斂條件結束

3 理論分析

本章從兩方面分析算法RASC。首先，證明在每次迭代中通過算法1 計算的結果保證式（1）的目標函數值是不增的。其次，為了證明算法的有效性，分析了RASC 的計算復雜度。

3.1 收斂性分析

首先介紹在文獻[25]中提出的以下引理：

引理1對任意正數a和b，以下不等式成立：

命題1通過算法1 優化模型，式(1)中目標函數在每次迭代中是不增的。

證明定義為每次迭代后M(v),U(v),V的取值。首先證明更新得到的不會增加函數值。令：

即式（1）中目標函數在每次迭代中是不增的，命題1 成立。

3.2 計算復雜度分析

由于算法RASC 的求解是用迭代方式進行的，可以通過對每個子步驟的計算復雜度求和來計算它們的總計算復雜度。求解每個子步驟的時間復雜度如下所示：

式（7）是更新自權重系數α(v)，其計算復雜度為O(d×n×(K+2))。

式（17）是更新共有表示V，其計算復雜度為O(min(Kn2,K2n)+K2n+d×(K+1)×n)。

假設T為迭代次數，則RASC 的計算復雜度為：

4 實驗設計與結果分析

本章將RASC 算法與其他算法進行了比較。由于都是無監督算法，用聚類來評價算法的效果。設計了四組實驗：第一組實驗包含了在多個數據集上的聚類結果；第二組實驗是一些關于收斂性的實驗結果；第三組實驗分析了不同參數取值下對實驗結果的影響；第四組實驗比較了所有算法花費的時間。

4.1 數據集概述

為了評估本文RASC 算法的有效性以及對不同的多視圖數據集的兼容性，選取了6 個數據集來進行實驗，分別是：MvYale、Scene15、KSA、Handwritten numerals、Caltech101_7 和MSRC_v1。表3 列出了這些數據集的簡要總結，而具體描述如下所示。

（1）MvYale數據集

MvYale 是一個由耶魯大學創建的人臉數據集，它包含了15 位志愿者的165 張圖像。該數據集是一個灰度數據集，其圖像主要包括燈光、面部表情和姿勢的變化。為了有效分析數據，提取了5類特征：SIFT（scale-invariant feature transform）、HOG（histogram of oriented gradients）、LBP（local binary pattern）、WT（wavelet texture）和GIST。

（2）MSRC_v1 數據集

MSRC_v1 數據集包含了屬于8 種類別的240 張圖像。選取了其中的7類（tree，cow，building，airplane，face，car，bicycle），并且每種類別包含30 張圖像。提取了6 類特征，分別為：LBP、HOG、GIST、CENTRIST、CMT（color moment）和SIFT。

（3）Caltech101_7 數據集

Caltech101數據集包含了屬于101種類別的8 677張圖像。選取了其中被廣泛應用的7 種類別（Dolla-Bill，Faces，Garfield，Motorbikes，Snoopy，Stop-Sign，Windsor-Chair）。這個包含441 張圖像的子數據集被命名為Caltech101_7。對于每張圖像，提取了與MSRC_v1 數據集相同的特征。

（4）Handwritten numerals數據集

Handwritten numerals（HW）是一個含有10 種類別和2 000 張圖像的手寫數字數據集。本文提取了6類特征：Zernike moment（ZER）、pixel averages in 2×3 windows（PIX）、Karhunen-lovecoefficients（KAR）、profile correlations（FAC）、Fourier coefficients of the character shapes（FOU）和morphological（MOR）。

（5）Scene15 數據集

Scene15 是一個含有15 種類別（highway、inside of cities、tallbuildings、streets、suburb residence、forest、coast、mountain、open country、bedroom、kitchen、livingroom、store、industrial和office）和4 485 張圖像的數據集。對于每張圖像，本文提取了6類特征：SIFT、SURF（speeded-up robust features）、PHOG（pyramid HOG）、LBP、GIST 和WT。

（6）KSA 數據集

KSA 數據集包含了5 個動作，其中每個動作被視為一種類別。從每個動作中選取2 000 幀視頻，從而構成一個包含11 000 數據的子數據集。使用4 類姿態特征：fJJ_d,fJL_d,fLL_a,fPP_a。

4.2 實驗方案

為了評估本文RASC 算法的效果，在實驗部分對比多種經典的無監督多視圖聚類方法：

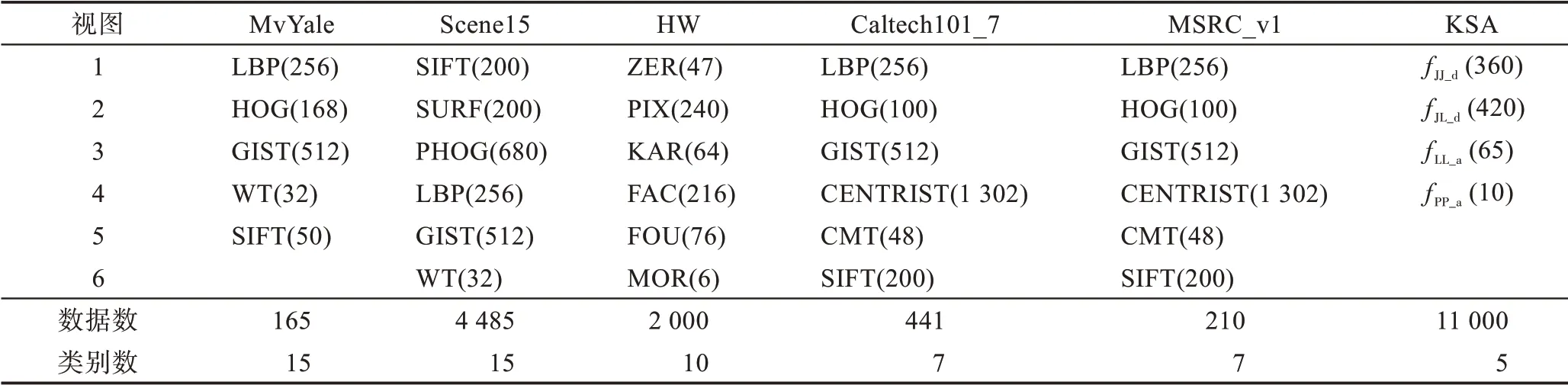
Table 3 Details of 6 used multi-view datasets表3 6 個多視圖數據集的詳細說明

（1）BSV（best single view）：將RASC 算法用到多視圖數據集的每個視圖上，然后選取最佳的結果作為最終結果。

（2）GSSMF（group structured sparsity matrix factorization）：文獻[18]提出的一種基于簇結構稀疏的矩陣分解的多視圖聚類算法。

（3）MultiNMF：文獻[11]提出的最經典的基于非負矩陣分解的多視圖聚類算法。

（4）GNMF（multiview non-negative matrix factorization with graph regularization）：文獻[12]提出的一種帶局部圖正則約束的基于非負矩陣分解的多視圖聚類算法。

（5）EquiNMF：文獻[19]提出的一種無參數的帶全局圖正則約束的基于非負矩陣分解的多視圖聚類算法。

（6）MVSE（multi-view spectral embedding）：文獻[26]提出的一種基于圖學習的多視圖聚類算法。

（7）AMGL：文獻[20]提出的一種無參數自加權圖學習的多視圖聚類算法。

由于RASC 算法和對比方法均是無監督多視圖算法，因此采用K-均值聚類（K-means）算法來評估聚類效果。又K-means 初始值的不同會影響算法的穩定性，因此采用一種固定初始化的K-means 算法。聚類算法有不同的評價指標，選取精度（Accuracy，ACC）、歸一化互信息（normalized mutual information，NMI）和F值（F-measure）這3 種評價指標來展示實驗結果。算法的精度為10 次運行結果的均值，并且每個數據集上實驗效果最好的方法結果用加粗表示。

4.3 實驗結果分析

表4 至表6 展示了8 個聚類方法在6 個多視圖數據集上的分別在ACC、NMI 和F-measure 這3 種評價指標上的實驗結果。接下來將對實驗結果進行深入的分析。

Table 4 ACC of different clustering algorithms on multi-view datasets表4 不同聚類算法在多視圖數據集上的ACC 值

Table 5 NMI of different clustering algorithms on multi-view datasets表5 不同聚類算法在多視圖數據集上的NMI值

Table 6 F-measure of different clustering algorithms on multi-view datasets表6 不同聚類算法在多視圖數據集上的F 值

（1）對于評價指標ACC，本文方法RASC 在5 個數據集上取得了最好的效果，在數據集KSA、Handwritten 和Scene15 數據集上取得了5%以上的性能提升；對于評價指標NMI，本文方法RASC 在4 個數據集上取得了最好的效果，并且在評價指標ACC 高提升的3 個數據集上也取得了5%左右的性能提升；對于評價指標F-measure，本文方法RASC 在5 個數據集上取得了最好的效果，在MvYale、Handwritten 和Caltech101_7 數據集上取得了5%左右的性能提升，而在KSA 和Scene15 數據集上取得了10%左右的性能提升。這些實驗效果可以證明本文方法的有效性。

（2）從表4 至表6 中可以看到，對于ACC、NMI 和F-measure 這3 種評價指標，本文方法RASC 與基于矩陣分解的多視圖子空間聚類方法相比，基本穩定提升了5%的精度，在某些數據集上提升了近10%的精度。這充分說明了本文創新點的合理性：即在數據的大誤差和小誤差之前做權衡，而且在不同視圖之間做了自權重系數。這確實提升了基于矩陣分解的多視圖子空間聚類算法的效果。

（3）可以看到基于圖學習的多視圖子空間聚類算法MVSE 和AMGL 的部分評價指標在MSRC_v1和MvYale 數據集上取得了比本文方法RASC 更好的效果。這是因為本文模型屬于線性模型，而MVSE 和AMGL 的模型屬于非線性模型，即對于某些非線性數據集來說，它們的實驗效果確實優于RASC。但是它們的時間復雜度比RASC 高一個量級，而且MVSE和AMGL 盡管有一定的魯棒性，但是RASC 是設定參數來平衡兩種誤差，從實驗結果可以看出RASC 在部分數據集上效果要優于MVSE 和AMGL。

4.4 收斂性分析

為了驗證本文算法的收斂性，在圖1 中繪出本文算法在MvYale、Caltech101_7、MSRC_v1 和KSA 這4個數據集上的迭代收斂曲線。通過對迭代收斂曲線的分析，本文算法在迭代過程中是非遞增的并且會逐漸收斂到一個固定值。此外，算法經過15 次左右的迭代后，目標函數值的變化就不明顯了，這說明本文算法收斂效率很高。

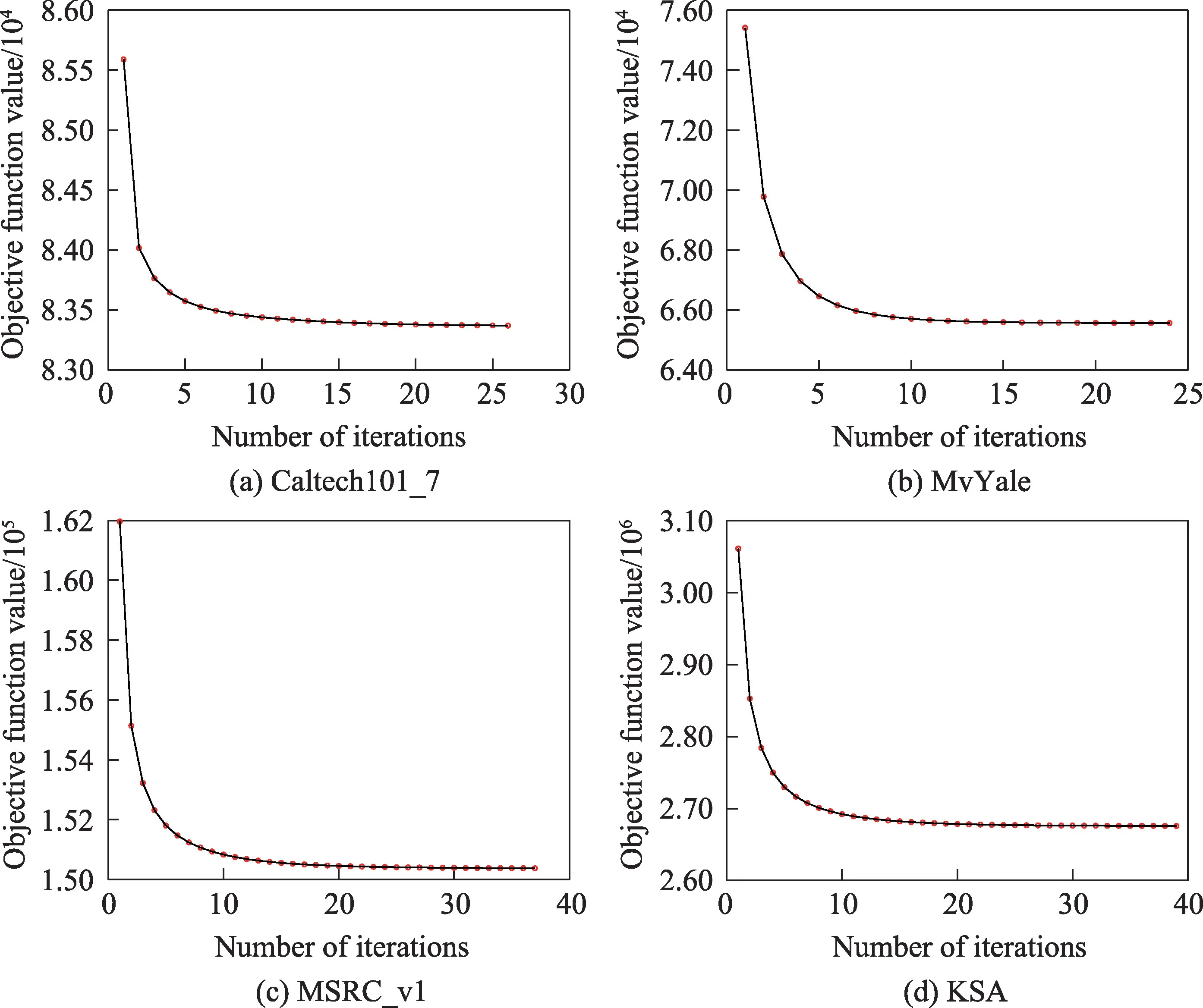
Fig.1 Convergence curves of RASC on 4 datasets圖1 RASC 在4 個數據集上的收斂曲線

4.5 參數敏感性分析

對于參數敏感度的分析，本文在兩個數據集上設計了實驗：MSRC_v1 和Scene15。將參數λ的取值區間設為[10-3,10-2]，并分別分析了參數λ對3 個評價指標的影響，詳細結果如圖2 所示。

通過對實驗結果的分析，有以下結論：首先，不同參數的實驗效果并不相同，這說明參數選擇的重要性。從圖2 的抖動性來講，可以看到參數λ的取值很大程度上影響著實驗結果，這說明本文模型對參數λ還是非常敏感的。其次，可以看到當參數λ的取值比較大時，模型精度的變化很小，這也符合本文模型的設定，即當參數λ比較大時，盡可能地使得近似矩陣M(v)逼近數據矩陣X(v)，此時模型的第一項對模型性能的影響很小，即效果會趨近于穩定。

4.6 時間復雜度分析

在表7 中比較了RASC 及其對比方法在6 個數據集上的10 次運行時間的均值。通過對實驗結果的分析，有以下結論：

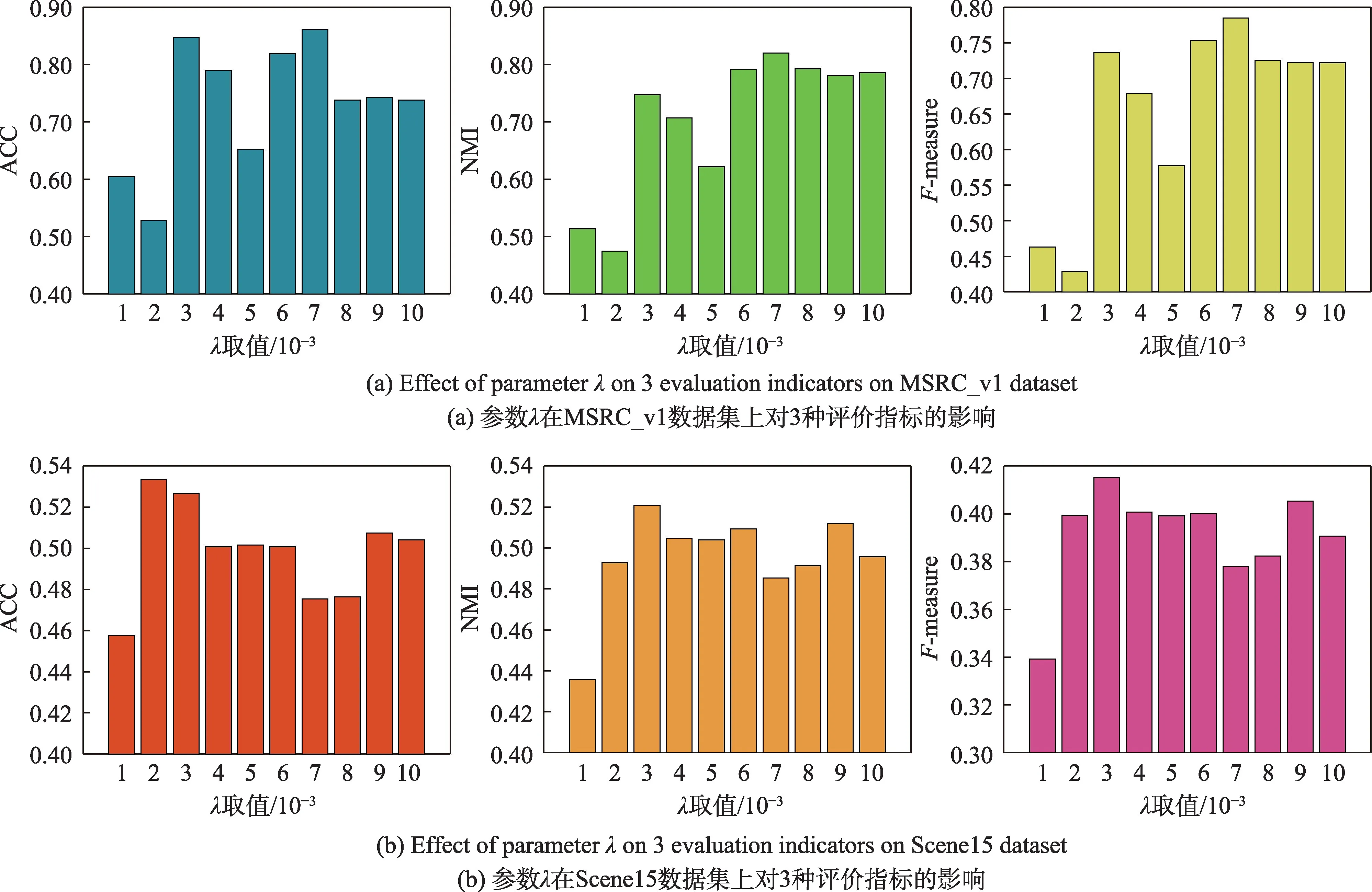
Fig.2 Sensitivity analysis on parameter λ圖2 參數λ 的敏感度分析

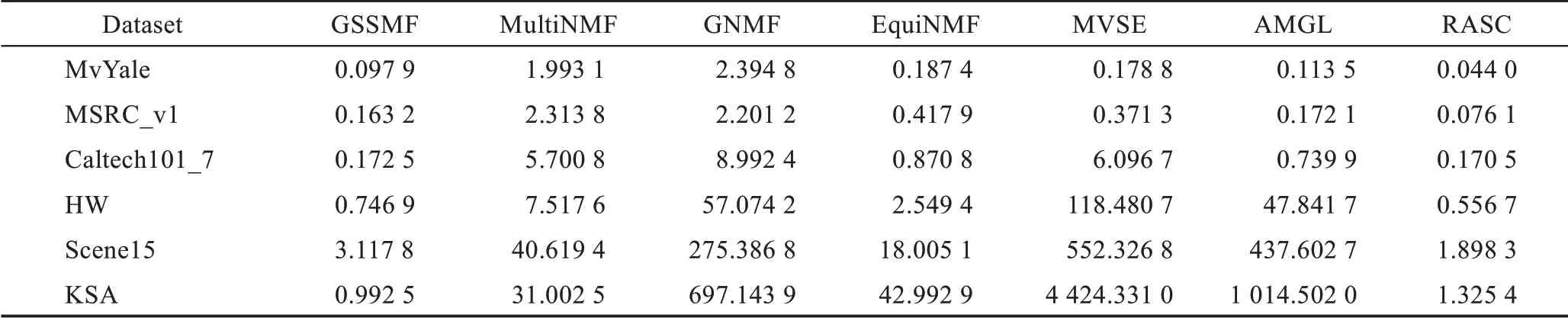
Table 7 Average running time on 6 datasets表7 在6 個數據集上的平均運行時間 s

從表7 中可以分析出本文算法在大部分數據集上花費的時間在所有算法中是最少的，這充分說明了本文算法具有比較高的計算效率。相比于計算復雜度為O(n3)的MVSE 和AMGL 來說，RASC 在大部分數據集上所花費的時間比較少是理所應當的。而相比于基于非負矩陣分解的GSSMF、MultiNMF、GNMF 和EquiNMF來說，RASC所花費的時間依舊要少，這說明本文算法的高效性。

5 結束語

本文提出了一種魯棒自加權的多視圖子空間聚類算法。為了更好地學習多視圖的共有表示，從多視圖魯棒性入手，同時考慮離群點和小誤差對模型的影響，使得學得的共有表示能夠更好地擬合數據。并且受AMGL 算法的啟發，引進自加權的思想，即為每個視圖提供自適應性權重，刻畫了視圖的不同重要性。進一步分析了算法的收斂性，理論和實驗結果都證明了RASC 可以收斂。最后，豐富的實驗結果表明：本文RASC 算法比其他多視圖子空間聚類算法更有效。

在本文模型中需要調節平衡因子λ。因此未來的第一個工作是如何自動調節該平衡因子或者給出一種合理的求解策略。由于本文模型是非光滑非凸模型，在本文中只能證明RASC 收斂，并不能證明RASC 收斂到局部極小值。因而未來的第二個工作是如何使得該模型盡可能地收斂到局部極小值甚至收斂到全局最小值。