SCVerify：抗功耗側信道攻擊軟件實現的驗證

張 俊

1.中國科學院 上海微系統與信息技術研究所，上海200050

2.上海科技大學 信息科學與技術學院，上海201210

3.中國科學院大學，北京100049

+通信作者E-mail:zhangjun@shanghaitech.edu.cn

現代社會生活中，密碼算法已經廣泛應用于嵌入式計算設備，以構成其安全機制的支柱，嵌入式設備中硬件和軟件系統的安全性分析變得越來越重要。一般來說，安全性是建立在攻擊者只能訪問輸入輸出，但是不能訪問到中間計算結果的基礎上。不幸的是，攻擊者可以通過分析側信道物理泄露信息，通過統計分析的方法來獲得相關中間計算結果，從而推算出加密密鑰。這些所謂的側信道攻擊利用密鑰和計算設備的非功能屬性，如執行時間[1]、功耗[2]、電磁輻射[3]等的統計依賴性，其中，差分功耗分析（differential power analysis，DPA）是一種極受歡迎且有效的攻擊手段[4]。

到目前為止，已經有很多對策可以阻止側信道攻擊。針對功耗側信道攻擊，掩碼技術仍然是使用最為廣泛的一種技術，可以通過隨機化的方式打破密鑰和側信道泄露信息之間的統計依賴性。例如，對于一個敏感的密鑰變量k，使用布爾掩蓋，利用一個隨機變量r和異或操作⊕可以獲得一個掩蓋變量km=k⊕r，并且通過異或操作的可逆性可以利用相同的隨機變量r恢復出密鑰變量km⊕r=k。其他的隨機化掩碼對策有加法掩蓋km=k+rmodn，乘法掩蓋km=k*rmodn。雖然已經有了各種掩碼的實現方式，如用于AES（advanced encryption standard）或其非線性組件（S-box）[5-7]，但是檢查它們是否正確總是很困難且容易出錯。因此，形式化驗證這些掩碼對策的正確性是十分重要的。

在這之前，主要有兩種類型的掩碼對策驗證方法：一種是基于類型推導[8-9]的；另一種是基于模型計數[10-11]的。基于類型推導的方法快速而健全，它們可以快速證明計算是無側信道信息泄漏的。例如，當需要驗證的計算在句法上是獨立于密鑰的或已被從未使用的隨機變量掩蓋。可是句法類型推導并不完整，因為有些計算的句法類型推導結果是分布類型未知的。相比之下，基于模型計數的方法是完整的，它們檢查計算結果在統計上是否獨立于密鑰[5]。但是，由于模型計數的固有復雜性，它們在實踐中可能運行起來非常慢。在準確性和可擴展性方面，上述差距在最近的方法中尚未得到解決。

過去幾年，很多掩碼策略[5,7,12-13]發表出來，盡管它們在攻擊模型、掩碼模式、加密算法上有所不同，但是共同的問題是缺少一個高效的工具可以形式化地驗證這些策略的正確性[14]，本文的工作旨在解決這個問題。盡管有一些驗證工具也實現了相關功能[8,10-11,15-16]，但是它們要么是運行速度快卻不準確（例如以類型推導技術為基礎的方法），要么是準確但是運行速度慢（例如以模型計數為基礎的方法）。例如，Bayrak等[8]提出了一種泄露檢測方法去判斷計算結果是否在邏輯上獨立于密鑰和隨機變量，運行很快但不準確，并且很多存在泄露的節點被錯誤地證明了[10-11]。相比之下，Eldib 等[10-11]提出的基于模型計數的方法是準確的，但此方法需要構建的邏輯公式與隨機變量成指數關系，顯著地降低了可擴展性。本文的語義類型推導系統受到最近一些工作[15-16]的啟發，它們利用了一些可逆操作的獨特性質，然而，這些現有技術與本文的方法有著顯著的不同點，因為它們的類型推導規則是基于句法結構的，而本文的類型推導方法是基于語義的，并且可以通過SMT（satisfiability modulo theories）求解器去細化未知的推斷類型。

為解決現有技術要么快但不準確或準確但是運行慢的問題，本文提出了一種新的驗證掩碼對策的方法SCVerify。圖1 描繪了整個流程，其中輸入包括程序和標記為明文、密文、隨機變量的集合。首先將程序轉換為中間表示：數據依賴圖（data dependency graph，DDG）。然后，按照拓撲排序遍歷DDG 并利用類型推導方法以推斷每個中間計算結果的分布類型；接下來，根據分布類型檢查所有中間計算結果是否已經被完美掩蓋，如果其中任意一個無法以這種方式解決，調用基于SMT 求解器的模型計數程序，該程序利用可滿足性（SAT）或模型計數（SAT#）求解來驗證中間計算結果的分布類型，再將計算結果反饋回類型推導系統；最后，基于提煉的類型推導規則，繼續分析其他中間計算結果。

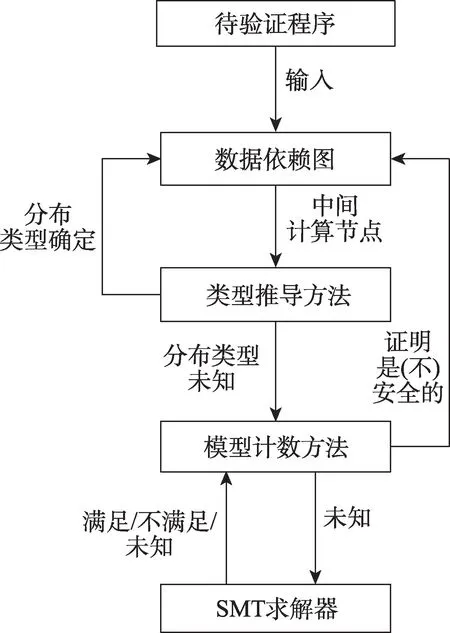
Fig.1 Overview of SCVerify圖1 SCVerify 流程圖

SCVerify 可以被視為類型推導方法和模型計數方法的集成。其中，類型推導受到相關工作[15-16]的啟發，它們旨在推導中間計算結果的分布類型。但是，有一個至關重要的區別：它們的推導規則是基于句法的且僅僅依賴于程序的結構信息。本文的推導規則是基于語義的，并且借助于SMT 求解器可以逐步提高準確性。從高層次說，本文的語義類型推導規則包含它們的句法類型推導規則。因此，綜合類型推導方法可以快速獲得驗證結果的優點以及利用SMT 求解器來解決未驗證的計算結果，本文的方法既準確又具備可擴展性。

1 基礎知識

1.1 側信道攻擊

假設需要驗證的程序實現了一個加密函數c←enc(p,k)，其中p表示明文，k表示密鑰，c表示密文，enc是加密函數。其中p、k、c都是有限長度的位向量，函數enc(p,k)的實現由以下計算序列組成：I1(p,k),I2(p,k),…,In(p,k)。It(p,k)是每一個中間計算結果，r是添加到加密函數enc(p,k)的實現中用來掩蓋密鑰k的一個隨機變量。在這里，r是一個均勻分布在域{0,1}s中的s位隨機數，使用隨機數r掩蓋密鑰k的目的是使所有中間計算結果在統計上與密鑰無關。當加密函數enc(p,k)在布爾域中關于密鑰k是線性相關的，可以利用enc(p,k⊕r)=enc(p,k)⊕enc(p,r)的事實，首先使用隨機變量r與密鑰k進行異或操作，然后解碼時利用enc(p,k⊕r)⊕enc(p,r)=enc(p,k)⊕enc(p,r)⊕enc(p,r)=enc(p,k)。在這種情況下，加密函數enc(p,k)無需做出改變。然而，當加密函數enc(p,k)是非線性函數時，掩碼和解碼的工作就會變得更加復雜，因為它們經常需要對加密函數enc(p,k)重新進行一次設計，手動設計這樣的掩碼對策工作量大且容易出錯，因而需要一個高效的自動化工具去評估掩碼對策到底有多安全。

針對每條運算指令的功耗泄露模型建模，漢明權重（Hamming weight，HW）是最通用和基礎的模型，它被廣泛應用于差分功耗分析。在這個模型中，嵌入式計算設備中執行一條指令的功耗在統計上依賴于這條指令操作數的漢明權重，一個位向量的漢明權重就是邏輯設置為1 的位數。同時，當知道程序中每個變量確切的寄存器地址的情況下，也可以插入更精確的功耗模型，如漢明距離（Hamming distance，HD）。漢明距離模型依賴于通過隨機變量改寫寄存器中的當前值和先前值中發生改變的位數數量。

在本文中，考慮的攻擊模型如下：假設攻擊者知道明文和密文的對應關系(p,c)，其中c←enc(p,k)。對于每對明文密文關系對(p,c)，攻擊者通過觀察側信道泄露信息可以知道最多d個中間計算結果I1(p,k,r),I2(p,k,r),…,Id(p,k,r)的聯合概率分布。然而，攻擊者不會知道隨機變量r，因為r是通過真實的隨機變量生成器生成的。攻擊者的目標是計算密鑰k。

1.2 概率性布爾程序

按照文獻[5,10-11]中的相關定義，假設程序Pro實現加密函數enc，如Pro:c←enc(p,k)。在程序Pro中，隨機變量r在掩蓋密鑰k的同時需要保持程序Pro 輸入輸出的不變性。在程序Pro 中，因為循環，函數調用和程序分支可以通過自動重寫去除[10-11]，整數變量可以轉換為位變量，出于驗證考慮，假設Pro 是一個概率性布爾程序并且其中每條指令都有一個唯一的運算符，最多有兩個操作數。

設K為密鑰集合，R為隨機變量集合，P為明文變量集合，C為存儲中間計算結果的集合，因此變量集是V=K?R?P?C。此外，該程序使用運算符集合op包括取反（?）、取并（∧）、取或（∨）、取異或（⊕），即op={?,∧,∨,⊕}。程序Pro 由一組中間計算結果表示：c1←I1(p,k,r),c2←I2(p,k,r),ci←Ii(p,k,r),…,cn←In(p,k,r),1 ≤i≤n。其中，r是一個均勻分布在域{0,1}s中的s位隨機數；在程序Pro 中使用它們的唯一目的是確保c1,c2,…,cn在統計上是獨立于密鑰k分布的。

定義1（數據依賴圖（DDG））對于程序Pro，定義數據依賴圖為Gpro=(N,E,λ)，其中N是節點集，E是邊集，λ是標記函數。

（1）N=L?Lv，L是程序Pro 中的指令集，Lv是程序中的葉子節點結合：lv∈Lv對應一個變量或常量v∈P?K?R?{0,1}，即程序Pro 中任意一個節點都可以用輸入的明文、密文、隨機變量、常量和相關的運算符表示。

（2）E=N×N，包含邊(l,l′)，當l:c=x?y，x和y由l′定義；當l:c=?x，x由l′定義。

（3）λ是l∈N到每對(val,op) 的匹配：當l:c=x?y，λ(l)=(c,?) ；當l:c=?x，λ(l)=(c,?) ；λ(l)=(c,⊥)對應每個葉子節點lv。同時，定義λ1(l)=c，λ2(l)=?。

圖2 給出了一個掩碼策略示例，其中K={k1,k2},R={r1,r2},P=?,C={c1,c2,c3,c4}。圖2 的左邊是一個類似C 語言的程序，只是其中⊕表示異或操作，∧表示取并操作，右邊是程序的數據依賴圖，圖中的各個節點表示如下：

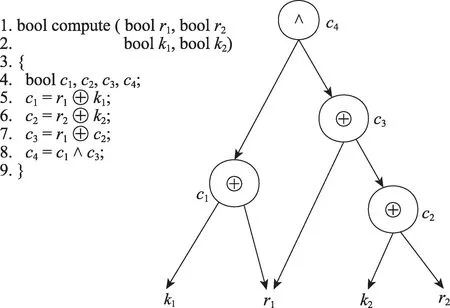
Fig.2 Example of masking countermeasure圖2 掩碼策略示例

對于節點c1，按照數據依賴圖的定義，有λ(c1)=(c1,⊕),λ1(c1)=c1,λ2(c1)=⊕。同時，對于任意一個節點l∈N，也可以用l.lft表示節點l的左孩子節點，用l.rgt表示節點l的右孩子節點，則有c1.lft=k1，c1.rgt=r1。

1.3 完美掩蓋

給出加密函數enc(p,k)一對明文密鑰對(p,k)，一個隨機變量r，d個加密函數的中間計算結果I1(p,k,r),I2(p,k,r),…,Id(p,k,r)。假設r是一個s位隨機變量，均勻分布在域M={0,1}s中，則使用Dp,k(M)表示I1,I2,…,Id的聯合概率分布，只要Dp,k(M)與密鑰信息k之間存在統計相關性，就認為加密程序Pro 是側信道攻擊不安全的。

定義2稱中間計算結果的d-set{c1,c2,…,cd}是：

（1）均勻分布，如果Dp,k(c1,c2,…,cd) 對于任意p和k是均勻分布的[10]。

（2）獨立于密鑰分布，如果對任意(p,k)和(p,k′)，都有Dp,k(c1,c2,…,cd)=Dp,k′(c1,c2,…,cd)[10]。

這兩者之間有一個區別：均勻分布總是獨立于密鑰分布，但是獨立于密鑰分布不一定是均勻分布。

定義3程序Pro 是order-d完美掩蓋的當且僅當程序Pro 的每一個k-set(c1,c2,…,ck)(k≤d)都是獨立于密鑰分布的。當程序Pro 是order-1 完美掩蓋的，簡稱程序Pro 是完美掩蓋的[10]。

2 基于語義的類型推導系統

在這一章中，首先介紹類型系統，該類型系統受到之前工作[15-16]的啟發；然后定義用于類型系統推導的相關數據結構；最后介紹具體的類型系統推導規則。

2.1 類型定義

定義T={CST,RUD,SID,NPM,UKD}為中間計算結果的分布類型集合，其中[c] 表示中間計算節點c←I(p,k,r)的分布類型。

（1）[c]=CST 表示c是一個常量，不存在側信道信息泄露風險；

（2）[c]=RUD 表示c是均勻分布的，不存在側信道信息泄露風險；

（3）[c]=SID 表示c是獨立于密鑰分布的，不存在側信道信息泄露風險；

（4）[c]=NPM 表示c不是完美掩蓋的，存在側信道信息泄露風險；

（5）[c]=UKD 表示c的分布類型是未知的，側信道信息泄露風險未知。

對于初始的葉子節點l∈LV其分布類型定義如下：若λ1(l)∈{0,1}，則[l]=CST；若λ1(l)∈P?K，則[l]=UKD；若λ1(l)∈R，則[l]=RUD。

2.2 輔助數據結構

在進行類型系統推導之前，需要定義相關的數據結構，用以支持類型系統的推導工作。相關定義如下：

定義4函數supp:N→K?R?P定義每個節點在數據結構上的支持變量。若λ1(l)∈{0,1}，則supp(l)=?；若λ1(l)=x∈K?R?P，則supp(l)=x；否則supp(l)=supp(l.lft)?supp(l.rgt)。因此，函數supp返回λ1(l)在結構上面依賴的變量集合。

定義5unq:N→R和dom:N→R是兩個函數，有以下兩點：

（1）對任意葉子節點l∈Lv，如果λ1(l)∈R，則unq(l)=dom(l)=λ1(l)，否則unq(l)=dom(l)=?。

（2）對任意中間節點l∈L，有unq(l)=(unq(l.lft)?unq(l.rgt))(supp(l.lft)?supp(l.rgt))；如果λ2(l)=⊕，那么dom(l)=(dom(l.lft)?dom(l.rgt))?unq(l)，其他情況下，dom(l)=?。

給出一個節點l，其對應表達式e由集合V中的變量定義，e在語義上依賴于一個隨機變量r∈V，當且僅當存在兩種不同的變量賦值π1、π2，對任意x∈V{r}，當π1(r)≠π2(r)，π1(x)=π2(x)，表達式e在π1、π2的賦值下取值結果不相同。

定義6函數semd:N→R定義一個節點l到在語義上有依賴關系的隨機變量的集合，這些隨機變量都是表達式為e的節點l在語義上依賴的。因此，有semd(l)?supp(l)，對任意r∈supp(l)semd(l)，λ1(l) 在語義上獨立于隨機變量r。

不像supp(l)，只是從程序中獲取節點的結構信息，可以直接通過句法推導得出，semd(l)則需要計算得出。提供一個使用SMT 約束求解器的方法去計算出對任意中間計算結果c←I(p,k,r)，任意隨機變量r∈R，判斷c在語義上是否獨立于變量r。特別的，將此方法形式化定義為一個可滿足問題（SAT），對應公式Θs如下：

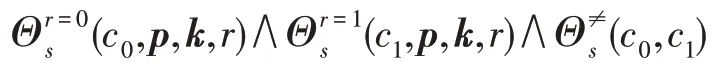
2.3 類型推導規則

根據在文獻[15-16]中的證明，對于任意中間計算結果c←I(p,k,r)，很容易得到以下結論：

（1）如果dom(l)≠?，那么[c]=RUD；

（2）如果隨機變量r∈R,r?semd(l)，那么[r⊕c]=RUD；

（3）如果[c]=RUD，那么[?c]=RUD；

（4）如果[c]=SID，那么[?c]=SID；

（5）對任意c′←I′(p,k,r)，如果semd(l)?semd(l′)=?,[c]=[c′]=SID，那么[c?c′]=SID。

下面給出本文基于以上觀察的語義推導規則（這里沒有使用NPM）：

當有多個規則可以應用于節點l∈N時，首先選擇可以推導出[l]=RUD 的規則。如果沒有規則可以應用在節點l，則[l]=UKD 。當上下文定義都清楚時，可以用[l]和[c]互換表示λ1(l)=c的分布類型。當前還沒有使用NPM 在推導規則中，在第3 章中會基于SMT 的模型計數的方法去處理語法類型推導結果為UKD 的節點，最后會明確其分布類型為NPM 還是SID，并反饋回類型推導系統中。本文的語義類型推導規則包含基于句法的類型推導規則，在驗證工具SCVerify 中，實際上首先會直接調用句法類型推導規則，這時只需要用supp函數替換語法推導規則中的semd函數即可，當發現句法類型推導結果為UKD時，需要先計算出semd，然后通過語法推導規則重新推導一遍。其實，本文的語法推導規則是對句法推導規則的補充，只有當語法類型推導結果同樣為UKD 的情況下，才會調用特別耗時的基于SMT 的模型計數方法。

Fig.3 Example of type inference圖3 類型推導示例

圖3 給出了一個類型推導示例，當使用supp進行句法類型推導時，結果為[r1]=[r2]=[c1]=[c2]=[c3]=RUD，[k]=[c4]=[UKD]；當使用semd進行推導，結果為[r1]=[r2]=[c1]=[c2]=[c3]=[c4]=RUD，[k]=UKD 。其中節點c4在句法類型推導的情況下分布類型為UKD，經過語法類型推導分布類型未RUD，語法類型推導可以很好地補充句法類型推導。

3 基于模型計數的細化方法

本章介紹利用基于SMT 求解器的技術逐步完善類型推導系統，添加SMT 求解器后可以讓已有的類型推導系統結果變得更加完整，可以證明一個待驗證的程序實現是否存在側信道信息泄露。

3.1 SMT 方法

對于一個中間計算結果c←I(p,k,r)，為了驗證其是否滿足完美掩蓋（定義3），可以將其約減到一個可滿足的邏輯公式（Ψ），定義如下：

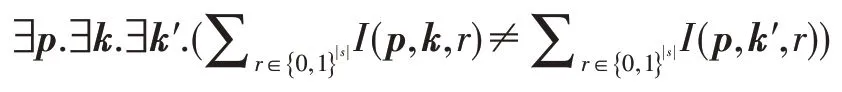
其中，r是一個均勻分布在域{0,1}s中的s位隨機數，表明公式I(p,k,r)的值為邏輯1 時隨機變量r的所有賦值情況的總和。當隨機變量r中的每個比特在集合{0,1}上是均勻分布的時候，是公式I(p,k,r)為邏輯1 的概率。因此，公式Ψ是不滿足的當且僅當中間計算結果c是完美掩蓋的。

按照Eldib[10-11]等提出的方法，將Ψ編碼為一個可以被現有的SMT 求解器解決的無量詞的一階邏輯公式，如下：

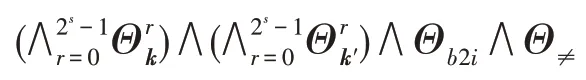
（2）Θb2i：轉換布爾結果的輸出為整數輸出（為true 轉換為1，為false 轉換為0），使得賦值的數量可以被計數。

（3）Θ≠：對于兩個不同的k和k′，判斷求和結果是否相同。

例如在圖2 中的節點c3=r1⊕c2=r1⊕(k2⊕r2)，其中(r1,r2)∈{(0,0),(0,1),(1,0),(1,1)}，由此可以構成求解節點c3是否被完美掩蓋的SMT 公式Ψ，其對應的四部分分別如下：

通過添加斷言((n=1)∧c)∨((n=0)∧?c)將布爾變量轉換為整型值，該斷言可以確保當布爾變量c的值為true 時，整型n=1；當布爾變量c的值為false 時，整型n=0。

盡管SMT 公式的大小和程序Pro 的大小是線性相關的，但是不同副本的數量和在計算中使用的隨機比特數成指數關系。因此，這個方法不能適用于大型程序。為了克服這個問題，之前的工作[10-11]提出一種約減方法用來減小公式大小。其主要思路如下：一個中間計算結果c←I(p,k,r)，對應DDG 中以節點l為根的子樹T，尋找一個在子樹T中的中間節點ls，滿足dom(ls)∩unq(l)≠?，這樣的一個節點稱之為割點。一個割點是最大的當且僅當沒有其他可以從l到ls的割點。如果ls是一個割點，那么存在一個隨機變量r∈dom(ls)∩unq(l)；因為r∈dom(ls)，dom(ls)≠?，則[λ1(ls)]=RUD；此外r∈unq(l)，表明當在判斷節點l的分布類型時λ1(ls)可以被看成是一個新的隨機變量。因此，可以用一個來自dom(ls)∩unq(l)中的隨機變量替換根節點為ls的在T中的子樹，這樣可以有效約減公式大小。

3.2 SMT 求解結果反饋回類型推導系統

考慮以下場景：類型推導系統推斷出節點l的分布類型[l]=UKD，但是以SMT 求解器推斷出其類型為NPM 或者SID。這些結果可以反饋回類型推導系統中，產生以下兩點益處：（1）標記更多的節點為完美掩蓋（RUD 或者SID）；（2）使得更多節點為NPM，這就意味著無需調用復雜的SMT 求解器去計算出這些節點的類型。更多的是，如果SMT 求解器得出節點l是完美掩蓋的，那么[l]=SID，將其反饋代入類型推導系統中可以幫助更方便地推導出依賴于節點l的其他節點類型。

另一方面，如果SMT 求解器得出節點l不是完美掩蓋的，則[l]=NPM，并將其反饋回類型推導系統，這樣可以推導出其他節點的類型也是NPM。為了實現上述的情況，增加了與NPM 相關的類型推導規則，如下所示。

帶有NPM 類型的語義推導規則：

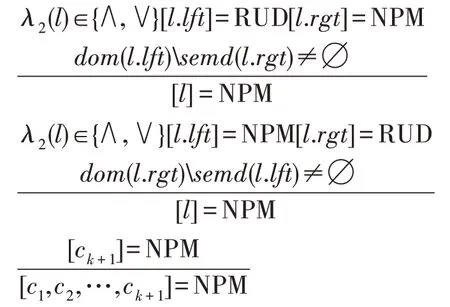
它們是對前文沒有使用NPM 類型推導規則的補充，這樣可以使得更多的NPM類型的節點通過類型推導系統推斷出來，避免調用耗時的SMT求解器去計算。

4 實驗

使用Z3[17]作為底層的SMT 求解器實現了文章中提出的細化的模型計數方法，并將其與語法類型推導系統進行整合，形成了一套命名為SCVerify 的驗證工具。為了比較實驗結果，在工具中也實現了句法類型推導方法[16]和以SMT 為基礎的方法[10-11]。在公開的可以獲得的加密軟件實現代碼上進行實驗，包括AES 和MAC-Keccak（message authentication code Keccak）中的代碼片段[10-11]。最終實驗結果表明：

（1）SCVerify 比之前的句法類型推導方法[16]更準確，可以解決在句法類型推導中分布類型為UKD 的無法確定的中間節點。

（2）SCVerify 比以SMT 為基礎的模型計數方法在保持相同準確率的情況下驗證大規模的程序時運行時間更短，相比于原先的運行時間，可以縮減50%以上。例如，SCVerify 驗證名為P12 的程序時只需花費幾秒鐘，然而以SMT 為基礎的方法需要花費超過1 h 的時間。

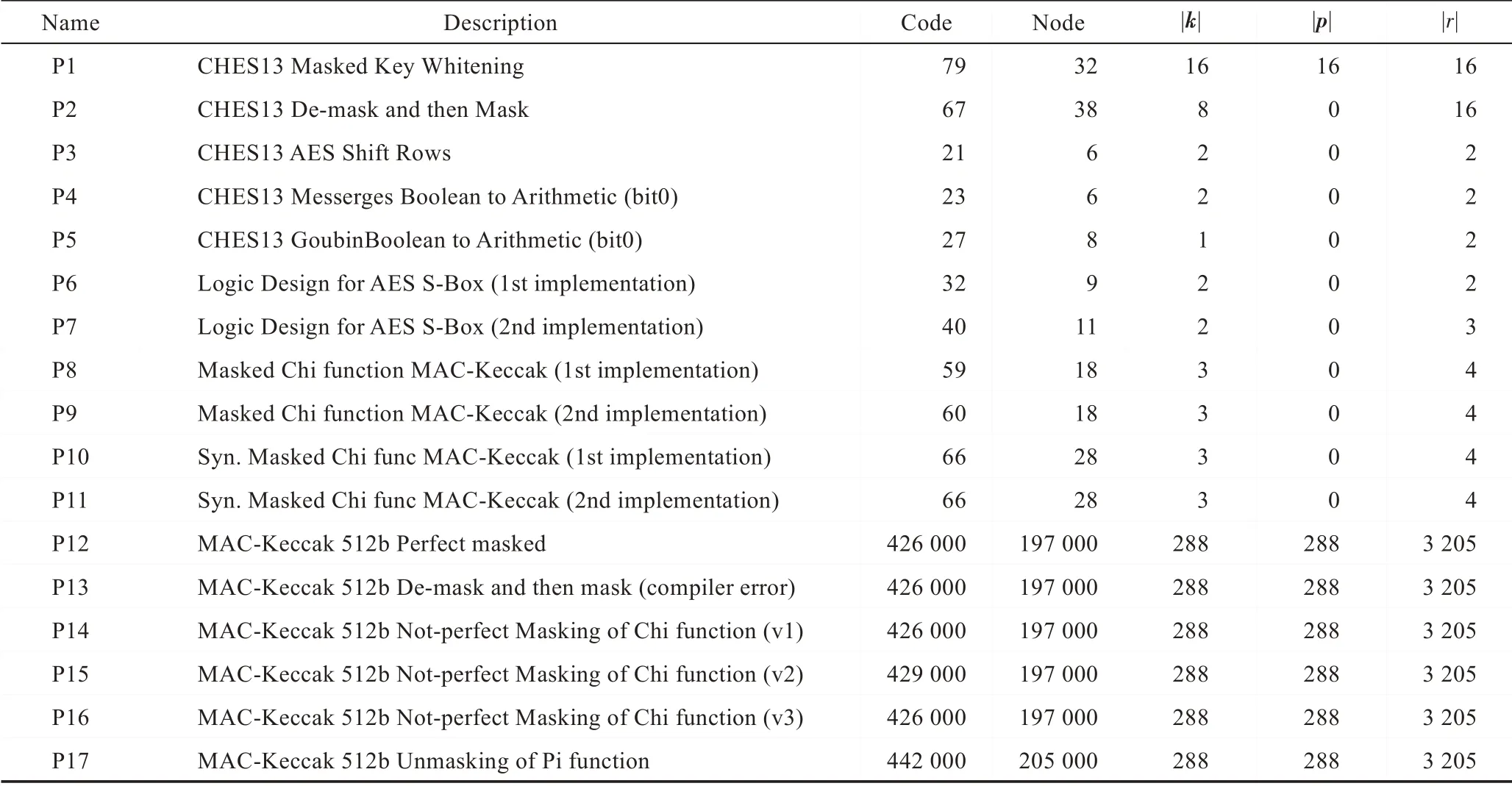
Table 1 Test case statistics表1 測試用例統計

4.1 測試用例

表1 展示了測試用例（P1～P17）的詳細情況，第一列是測試用例的名稱，第二列是測試用例的簡單描述，第三列表明程序中的運算指令數量，第四列表明程序轉換為DDG 后中間計算節點個數，第五列到第七列分別表示程序中總共的密鑰變量數量、明文變量數量、隨機變量數量，所有的統計數據都是在將程序轉換為概率性布爾程序之后的統計結果。其中P1～P5 是從文獻[8]中得出的掩碼用例；P6～P7 來自于文獻[5]；P8～P9 是MAC-Keccak 重新計算的例子，來自于文獻[18]；P10～P11 的掩碼例子來自于MACKeccak 中的Chi 函數；P12～P17 是幾個較大的測試用例，是從提交到NIST 主辦的SHA-3 組委會的MACKeccak 的示例代碼演化過來的。其中P13～P16 用不同的掩碼方式實現了Chi 函數；P17 實現了Pi 函數的掩碼解碼過程。

4.2 實驗結果

本文比較了SCVerify、句法類型推導的方法（記為Syn）[16]、以SMT 為基礎的模型計數方法（記為SMT）[10-11]的表現性能。表2 是Syn 與SCVerify 的對比實驗結果，第1 列表示測試用例的名稱，第2 列是Syn 方法中分布類型為UKD 的節點個數，第3 列和第4 列分別表示在Syn 方法中推斷節點的分布類型為UKD 時，在SCVerify 中將這些分布類型未知的節點明確為NPM 或SID 后，對應類型的節點數量。表2的實驗結果說明與句法類型推導方法相比，本文的方法是更準確的，可以消除在句法類型推導中分布類型為UKD 的節點，明確當前測試用例是否為完美掩蓋。表3 是SMT 與SCVerify 的對比實驗結果，第1列表示測試用例的名稱，第2 列和第3 列分布表示以SMT 為基礎的模型計數方法和SCVerify 的實驗時間，第4 列表示以SMT 為基礎的模型計數方法和SCVerify 判斷測試用例是否為完美掩蓋的測試結果是否保持一致。從表3 的實驗結果中可以很明顯地發現，與SMT 為基礎的模型計數方法相比較，本文方法在保證相同準確性的情況下，在大的測試用例中，可以縮短超過一半的時間。表4 展示了SCVerify 的具體結果集，第1 列表示測試用例的名稱，第2 列給出測試用例是否為完美掩蓋的值，第3 列～第6 列分別給出了測試用例對應的分布類型為RUD、SID、CST、NPM 的節點數量。SCVerify 可以準確地判斷出各個測試用例是否為完美掩蓋，并且給出具體的中間節點的分布類型統計結果。

Table 2 Comparison between Syn and SCVerify表2 Syn 與SCVerify 對比

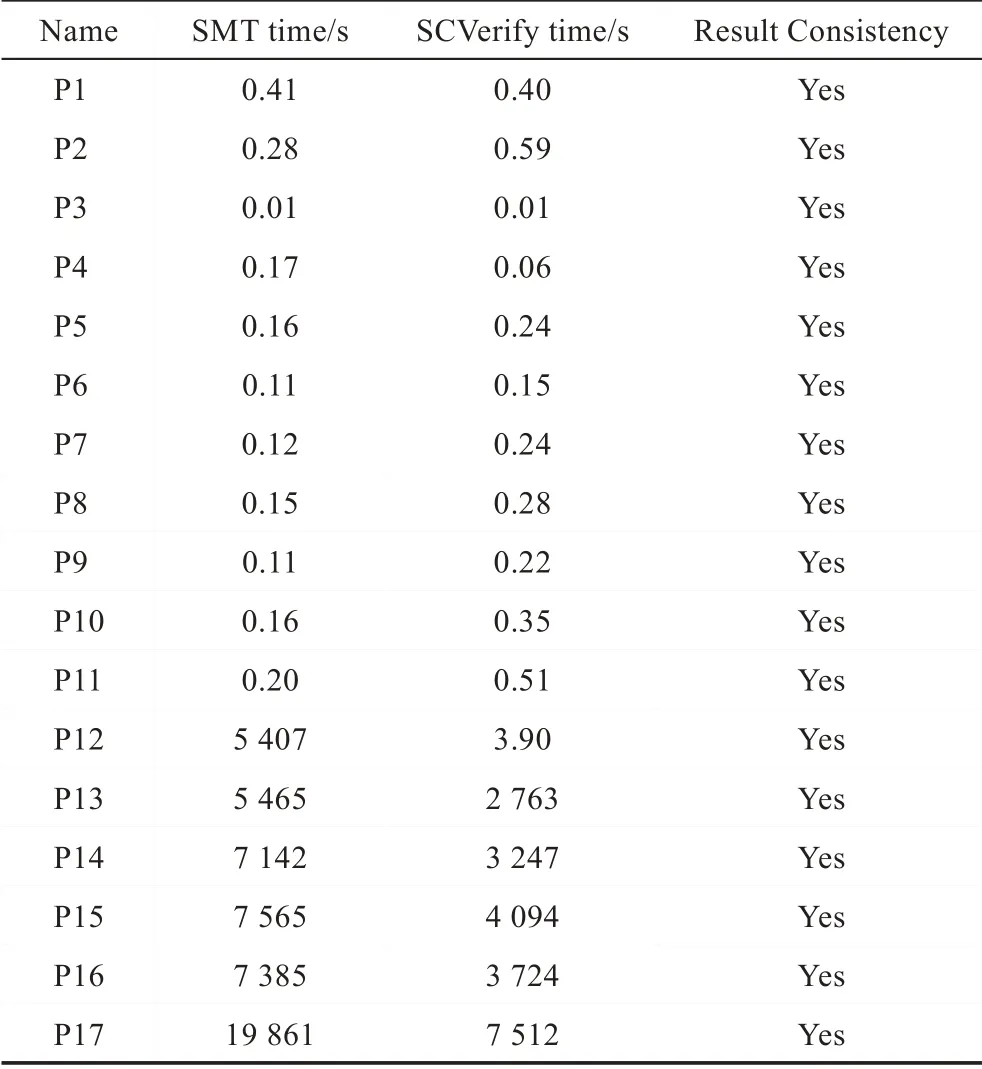
Table 3 Comparison between SMT and SCVerify表3 SMT 和SCVerify 對比

5 結論

本文提出了一種方法來證明一段加密軟件代碼的實現是否存在功耗側信道信息泄漏。該方法利用語義推導規則來推斷程序中每一個中間計算結果的分布類型，當發現語義推導規則不能明確某個中間結算結果的分布類型時，結合基于SMT 求解器的模型計數方法來逐步完善這些類型以提高準確性。已經實現了文中提出的方法并在相關密碼學測試用例上證明了它的有效性和正確性。實驗結果表明本文方法在效率和準確性方面優于當前最先進的驗證工具。

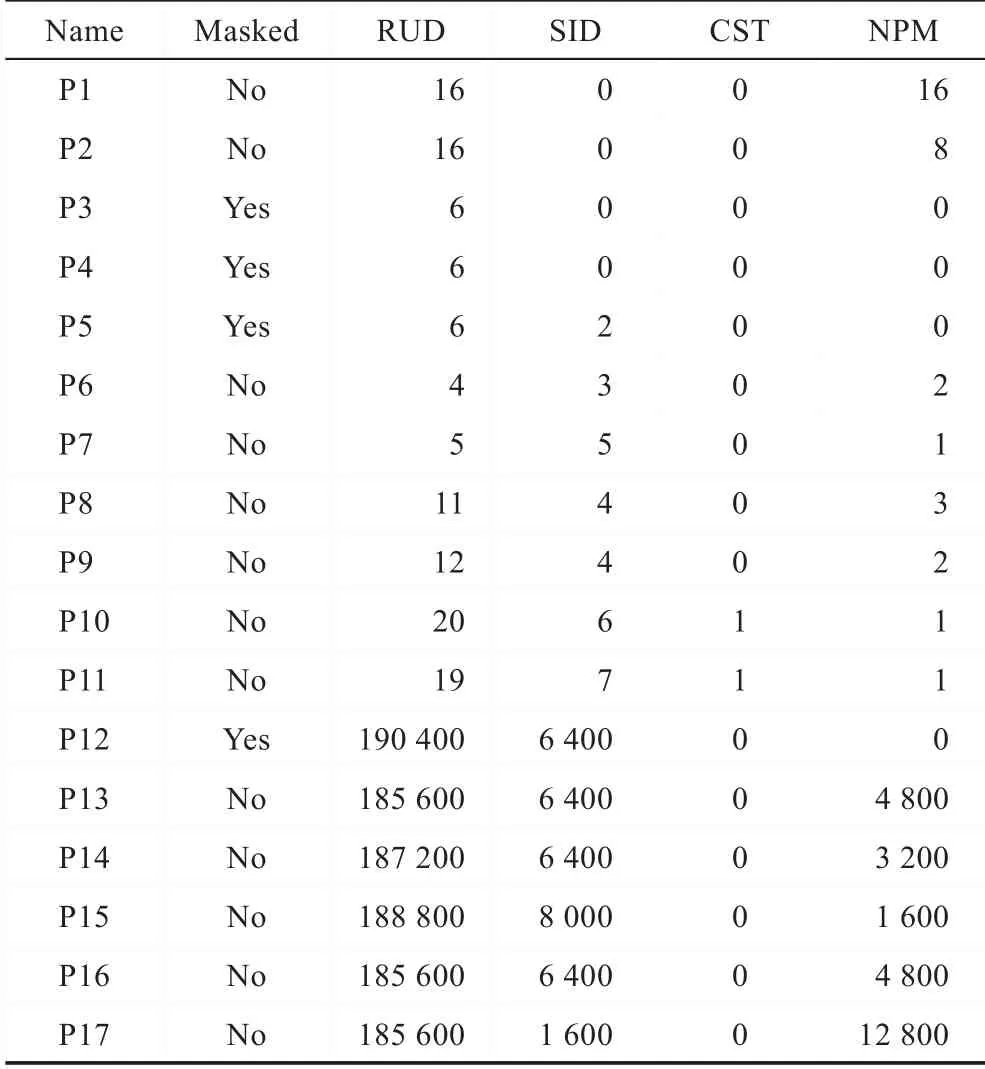
Table 4 SCVerify experimental results表4 SCVerify 實驗結果