馬尾松二元立木材積表的編制方法

汪乃武

（安徽省林業調查規劃院，安徽 合肥230031）

馬尾松（Pinus massoniana）是安徽省重要用材樹種之一，廣泛分布在淮河以南的黃山、宣城、池州、蕪湖、銅陵、馬鞍山、安慶、六安、合肥和滁州10個市；根據2015年安徽省森林資源規劃設計調查統計，全省現有馬尾松林地面積85.22萬hm2，蓄積量5 230.83萬m3。

立木材積表是計算林木材積和林分蓄積量的計量工具，數表的精確度直接影響使用數表區域森林資源調查結果的準確性和權威性[1]。安徽省目前使用的馬尾松二元立木材積表均為上世紀七十年代后期至八十年代初編制，當時計算機未普及，數表編制多采用圖式法編表，沒有準確數學表達式，不僅精度難以達到要求，而且使用也很不方便，加上當時各樹種品系、起源、經營方式與現代的差異，導致立木干型與樹種存在差異。因此，編制新一輪馬尾松二元立木材積表刻不容緩。

1 基礎數據收集與整理

根據馬尾松在安徽省的實際分布與生長狀況，同時按照編制二元立木材積表的總體要求，在不同立地條件、森林經營措施和齡組等綜合條件下選擇合適的樣地，保證所采集的各徑階樣木具有充分的代表性，且分布均勻。在選中的樣地內分徑階選取樣木，一塊樣地最多采集3個徑階，每個徑階最多采集一個樣木，選取生長正常、無斷梢、無分叉、主干明顯、干形中等的林木進行編表樣木的調查[2]。

本次編表共收集樣木723株，其中建模樣木533株、檢驗樣木190株，分布在6～40 cm的18個徑階內，起測直徑為5 cm。樣木伐倒后，以1 m（或2 m）為區分段進行區分，用測樹鋼圍尺量測樣木胸徑、各區分段中央直徑及梢底帶皮直經（精確到0.1 cm）等，用皮尺測量樹高（精確到0.1 m）。將外業調查測量的胸徑、樹高、各區分段的中央直徑及梢底直徑、梢頭長進行整理，建立數據庫，并按中央斷面積區分求積法計算各樣木的立木材積[2]。

2 二元立木材積表的編制

2.1 數據預處理[3]

將建模樣木和檢驗樣木分別按徑階計算其平均高（H）、平均材積（V）及相應的標準差（Sai），按照V（H）±3 Sai和散點圖將異常數據剔除，剔除率不超過5%為有效樣本。經過處理，共剔除10株樣木。其中建模樣木剔除8株，剔除率為1.5%；檢驗樣木剔除2株，剔除率為1.1%，樣本有效。最終建模樣木有效株數為525株，檢驗樣木188株。

2.2 模型的選擇、評價和確定

2.2.1 模型的選擇

圖1 胸徑-材積散點及擬合曲線

將上述525株有效建模樣木數據（di，Vi），以胸徑為橫坐標，材積為縱坐標繪制胸徑-材積的散點圖，如圖1所示。由散點圖的趨勢并結合有關要求，經過篩選，選擇下列①～⑤式作為編制安徽省馬尾松二元立木材積表的初選模型[3]，具體如下：

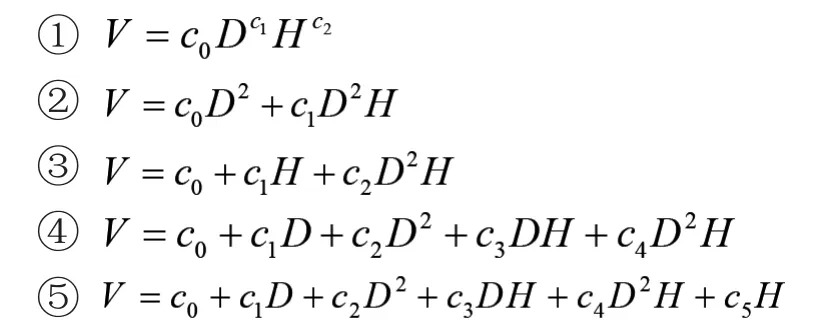
式中：V—材積；D—胸徑；H—樹高；c0、c1、c2、c3、c4、c5—待定參數。

2.2.2 模型的評價指標與方法

（1）評價指標。合理選擇并確立最優方程對于編制數表非常重要，因此需對初選模型進行評價。常用的評價指標主要有：離差平方和、相關指數、總相對誤差、相對誤差平均值、相對誤差絕對值平均值、預估精度和殘差圖分析等。

（2）評價方法。依據以下原則選定最優數學模型：離差平方和最小；相關指數最大；總相對誤差最小；相對誤差平均值最小；預估精度最大；殘差圖以橫軸為中心上下分布均勻。

當上述各指標不一致時，應優先考慮相對誤差平均值最小、相對誤差絕對值平均值最小、總相對誤差最小、殘差圖以橫軸為中心上下分布均勻的模型。

2.2.3 模型的擬合結果與參數檢驗

根據525株有效建模樣木數據，利用SPSS數據處理系統，按加權回歸（權函數為w=1/D4）求解上述各模型參數，并計算各評價指標值，其結果見表1、圖2。

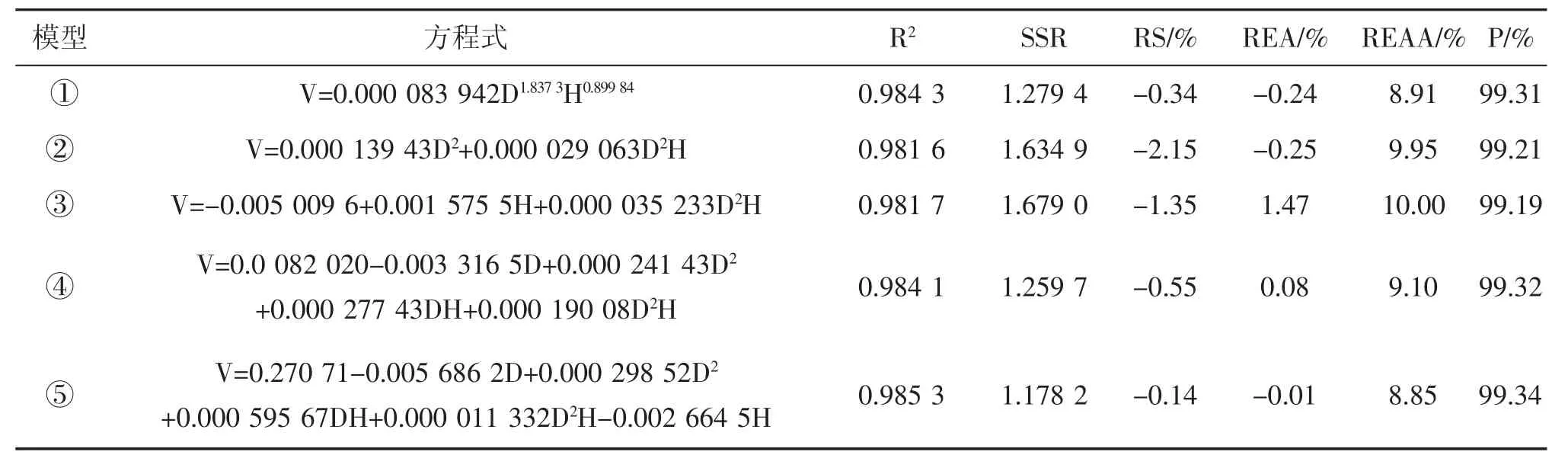
表1 二元立木材積模型參數及評價指標

由表1的P值及相關指數R2可以看出所選的5個模型的預估精度和相關性高，同時各模型的總相對誤差RS值均在（-3%，3%）范圍內，說明上述數學模型均為有效模型。

由表1各模型的對比分析可以看出，模型⑤各項指標最好，且其殘差圖分布最為均勻，但公式較為復雜，考慮公式相容性應選擇①式，且①式各評價指標僅次于⑤式，同時①式的殘差圖分布也較均勻（如圖2）。綜合考慮各因素，故選用模型①：V=0.000 083 942D1.8373H0.89984作為本次編制馬尾松二元立木材積表的最優回歸模型。

3 適用性檢驗[3]

圖2 馬尾松二元立木材積模型殘差

模型的適用性檢驗包括總相對誤差、相對誤差絕對值平均值和F檢驗。

總相對誤差：

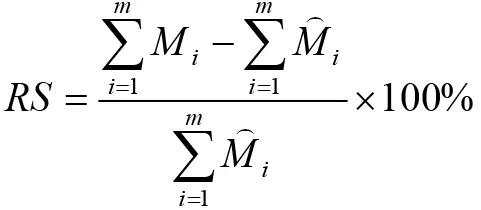
式中：Mi—檢驗樣本材積實際值；—檢驗樣本材積估計值；m—檢驗樣本數。

相對誤差絕對值平均值：

式中:REAA—相對誤差絕對值平均值。

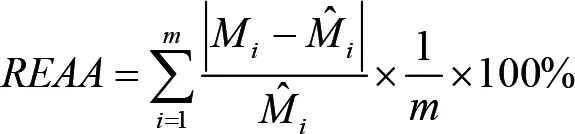
F檢驗：

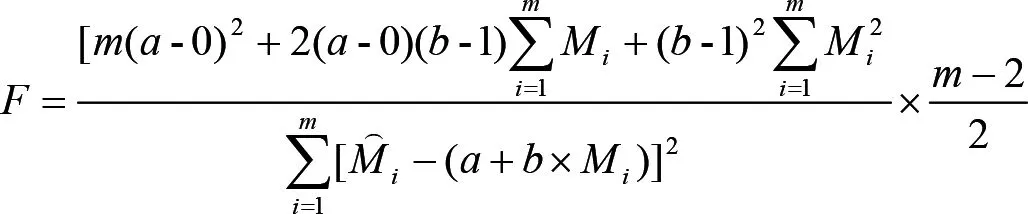
式中：F—服從自由度f1=2、f2=m-2的F分布。

當F＞F0.05時，推翻假設，說明a不等于0，b不等于1，檢驗樣本實際值和估計值存在顯著差異，胸徑—材積數學模型不適用；

當F≤F0.05時，說明a等于0，b等于1，檢驗樣本實際值和估計值沒有顯著差異，胸徑—材積數學模型適用。

3.1 模型適用條件[3]

RS絕對值小于等于3%；REAA小于10%；通過F（0，1）檢驗（檢驗統計量F≤F0.05），檢驗樣本實際值與估計值沒有顯著差異。

3.2 模型檢驗結果

將188株檢驗樣木的胸徑和樹高帶入上述所確定的最優二元立木材積回歸模型①中計算樣木材積估計值，計算適用性檢驗的指標值。結果表明，檢驗樣本的總相對誤差RS=0.26%，在（-3%，3%）范圍內；REAA=9.50%，小于10%；F（0，1）檢驗的F=0.8232，小于F0.0（52，186）=3.04；說明檢驗樣木實際值和估計值沒有顯著差異，所選數學模型適用。

綜上所述，利用馬尾松二元立木材積回歸模型①：V=0.000 083 942D1.8373H0.89984編出的安徽省馬尾松二元立木材積表是適用的，能夠為林業生產實踐提供參考。

4 編表結果

將胸徑各徑階值和樹高值代入回歸模型V=0.000 083 942D1.8373H0.89984中，即可得出相應的材積理論值，將求算的材積理論值與對應的直徑和樹高值整列成表，即得到安徽省馬尾松二元立木材積表（見表2）。

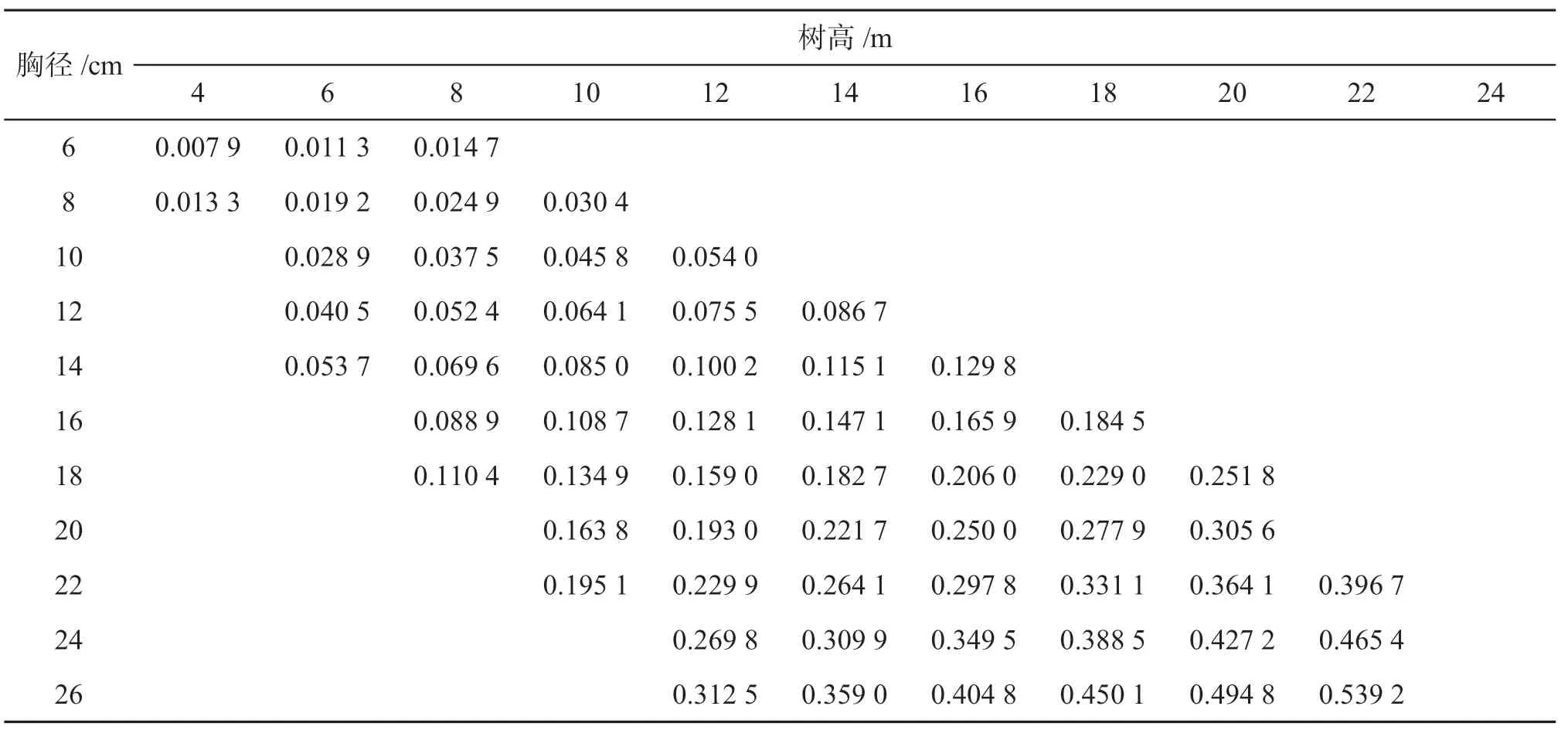
表2 安徽省馬尾松二元立木材積表/m3

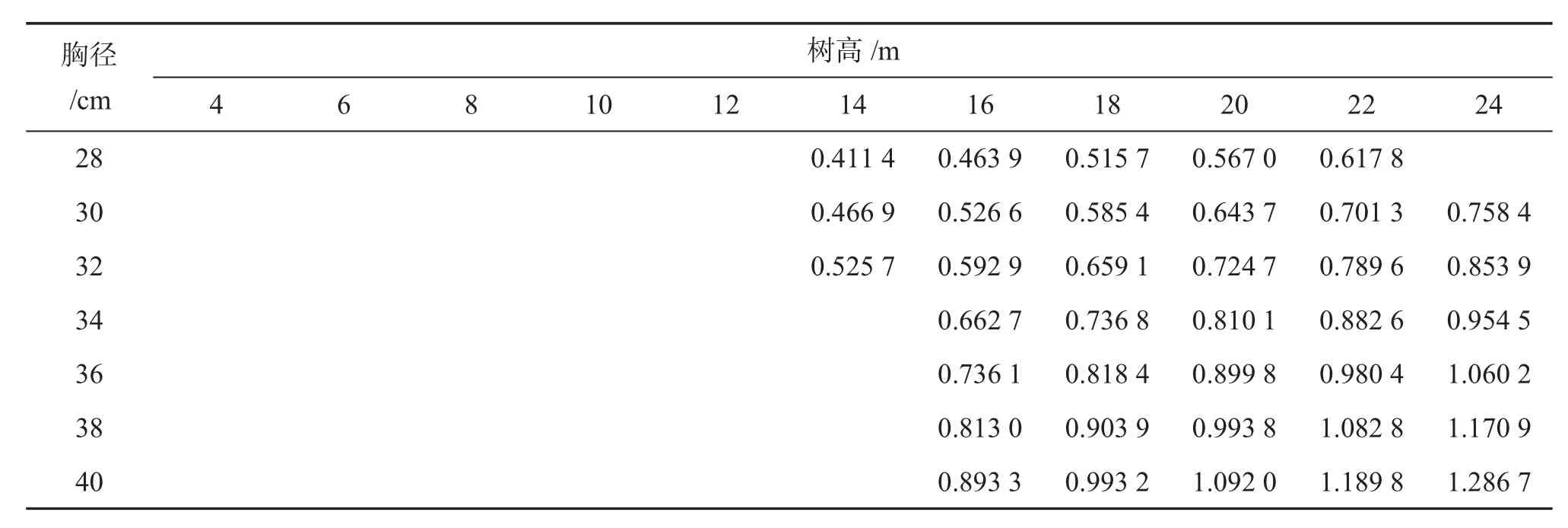
（續表2）

5 結論

（1）二元立木材積表是以胸徑、樹高為自變量，立木材積為因變量建立的函數關系，其適用性主要取決于建模和檢驗樣本的數量及來源是否具有代表性。本次525株建模樣木和188株檢驗樣木均取自于不同的區域、立地條件和經營管理水平，具有充分的代表性[4]。

（2）利用525株建模樣木數據，建立5種常用的二元立木材積數學模型。用非線性麥夸特迭代求解法確定最優馬尾松二元立木材積表模型為:V=0.000 083 942D1.8373H0.89984，綜合分析該模型的各項評價指標表現最好。

（3）用獨立采集的188株樣本對模型進行適用性檢驗。通過計算二元材積表理論材積與實際材積的總相對誤差為RS=-0.26%，在（-3%，3%）范圍內；REAA=9.50%，小于10%；F（0，1）檢驗的F=0.823 2，小于F0.0（52，186）=3.04；說明檢驗樣木實際值和估計值沒有顯著差異。因此，本研究編制的馬尾松二元立木材積表，可以在林業生產實踐中推廣應用。