預制裝配式箱涵數值模擬研究

肖 驍

(遼寧省交通規劃設計院有限責任公司 沈陽市 110166)

在公路建設施工過程中，小橋涵是影響整個工程造價、質量和工期的關鍵因素之一。目前，我國公路建設以蓋板涵、圓管涵等為主，因施工方法、工藝、材料單一，使得施工效率低下，建設周期較長，質量難以保證[1]。

預制裝配式箱涵具有如下優點：

(1)預制裝配式箱涵的快速化裝配能夠縮短工期，從而帶來直接以及間接的經濟效益。

(2)工廠化生產能夠更有效地控制施工質量，避免外界環境或者施工人員主客觀的影響。

(3)預制裝配式箱涵同時可以簡化設計過程，縮短設計時間。

(4)若采取的措施得當，預制裝配式箱涵的病害少，可維護性好，節約維護成本[2]。

以預制裝配式箱涵4.0×2.7m為例，結合有限元軟件Midas，對其進行結構分析研究。

1 有限元模型建立

裝配式鋼筋混凝土箱型通道、涵洞具有多重結構型式。考慮吊裝重量因素，本裝配式箱涵1-4×2.7為四構件組合結構，尺寸如圖1所示，其中預制裝配箱涵頂板、側墻均采用預制結構，底板采用現澆結構[3]。

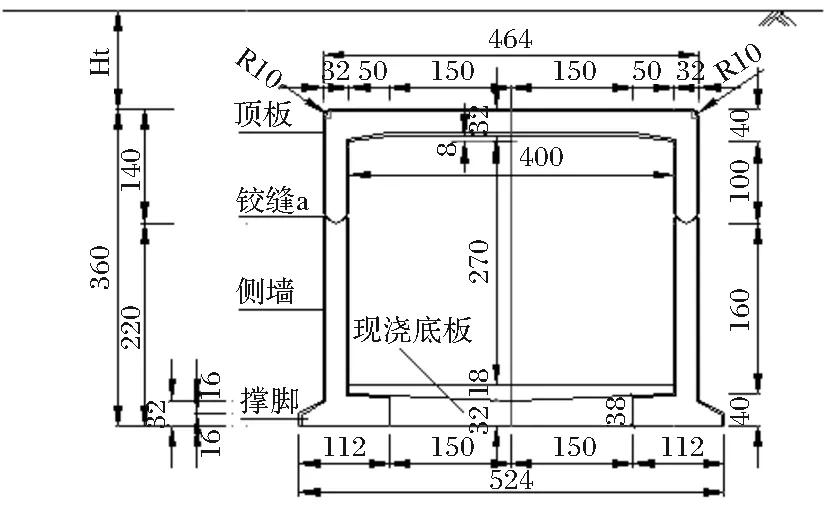
圖1 4×2.7m涵洞結構尺寸圖

1.1 計算假設

(1)平面假設

由于涵洞、通道等構造物的縱向長度遠大于其橫斷面尺寸，且所受的主要外力與其縱向垂直，對于1～3m一段的標準管節來說，完全可以將其視為平面應變問題，采用相應的計算理論(Levy(列維)方程：▽2(σx+σy)=0)以及有限元計算程序進行分析和計算。

(2)彈性地基假設

構造物與周圍土體之間是存在相互作用的[4]。合理的分析方法，原則上應該以地基、基礎、上部結構之間必須同時滿足靜力平衡和變形協調兩個條件為前提。只有這樣，才能揭示它們在外荷載作用下相互制約、彼此影響的內在聯系，從而達到安全、經濟的設計目的。

由于構造物與周圍土體在剛度上存在一定的差異，因此，無論是將周圍土體視為絕對剛性還是視為絕對柔性都是不正確的。應將周圍土體與構造物的接觸面視為彈性接觸，即：可將周圍土體假設為彈性地基。

三種常用的線彈性地基模型為：文克勒(Winkler)地基模型、彈性半空間地基模型與分層地基模型。借鑒線彈性地基模型，以及《公路橋涵地基與基礎設計規范》(JTG D63—2007)附錄P中“非巖石地基水平向抗力系數”的力學概念，可以確定出彈性地基的地基系數。

1.2 計算參數

(1)混凝土：重力密度γ=26.0kN/m3，彈性模量為Ec=3.25×104MPa，泊松比Vc=0.2，溫度線膨脹系數為0.00001，軸心抗壓強度標準值fck=26.8MPa，抗拉強度標準值ftk=2.40MPa，軸心抗壓強度設計值fcd=18.4MPa，抗拉強度ftd=1.65MPa；

(2)瀝青混凝土：重力密度γ=24.0kN/m3；

(3)鋼筋：鋼筋模量Es=2.0x105MPa，泊松比Vs=0.3，溫度線膨脹系數為1.2e-5，受拉區鋼筋抗壓強度設計值fsd=330MPa，受拉區鋼筋抗壓強度設計值fsd'=330MPa；

(4)非巖石地基樁端處的地基豎向抗力系數的比例系數m0=15000kN/m4，同時不考慮側向填土對于結構變形的約束作用；非巖石地基豎向地基系數：C0=m0×h(h為計算點處的埋深(m))。

1.3 結構作用及組合

1.3.1永久作用

按《公路橋涵設計通用規范》(JTG D60-2015)4.1.1條的相關內容確定永久作用。

(1)結構重力：按照材料重度計算結構自身重力。

(2)土的重力：考慮涵洞最不利受力情況，采用“等沉面”理論進行計算。

《公路涵洞設計細則》(JTG/T D65-04-2007)9.2.2條規定：填土的重力對涵洞的豎向和水平壓力強度，可按下式計算：

豎向壓力強度：qv=K·γ·h

水平壓力強度：qH=λ·γ·h

式中：g為土的重力密度(kN/m3)；h為計算截面至路面頂的高度(m)；λ為側壓系數，且λ=tan(45°-φ/2)2，φ為土的內摩擦角(°)；K為系數。

1.3.2可變作用

(1)汽車荷載與汽車沖擊力

《公路涵洞設計細則》(JTG/T D65-04-2007)9.2.1條規定：公路涵洞設計應采用車輛荷載。重型車輛少的四級公路的橋涵，車輛荷載的效應可乘以0.7的折減系數；應考慮車輛荷載的多車道作用及車輪荷載的傳遞和分布；除填料厚度(包括路面厚度)大于或等于0.5m的暗涵不計沖擊力。因此計算中不考慮汽車荷載沖擊作用。

(2)汽車引起的土側壓力

《公路涵洞設計細則》(JTG/T D65-04-2007)9.2.3條規定：汽車荷載引起的土壓力采用車輛荷載加載。在計算涵洞頂上車輛荷載引起的豎向土壓力時，車輪按其著地面積的邊緣向下作30°角分布。當幾個車輪的壓力擴散線相重疊時，擴散面積以最外邊的擴散線為準。

1.4 計算模型

采用大型有限元通用計算程序Midas進行計算，按照3m標準節段建模，整個箱涵共有884個節點采用816個板單元。鉸接處采用釋放板端約束，底板邊界約束采用x、y、z三個方向節點彈性支撐；靜力荷載包括箱涵自重、覆土壓力、側土壓力、臺后活載土(車輛作用臺后產生的土壓力)；移動荷載采用車輛荷載(采用舊公路履帶車輛荷載類型)。同時，當填土高度較矮時，汽車荷載作用較大，因此考慮采用車道荷載進行結構驗算。

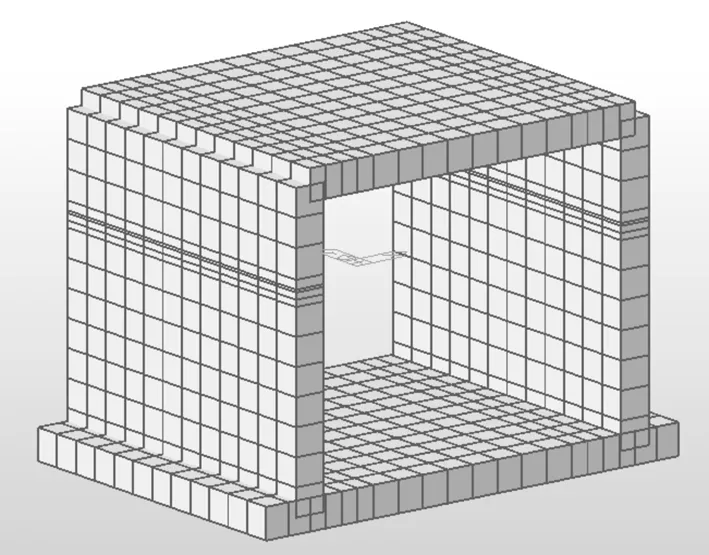
圖2 Midas建模示意圖

1.5 計算思路

本次結構計算過程在0.5～4.0m的填土高度范圍內，選取了4m填土高度作為計算臨界點。并通過Midas模型得到箱涵關鍵位置(跨中及角點等如圖3所示位置)處內力數值，按照偏心受壓構件分別進行各個構件結構承載能力以及使用性能的驗算，包括最小配筋率、受壓區高度、偏心受壓構件正截面、斜截面承載力驗算以及抗裂驗算等。同時，Midas模型中提取的內力均為單位寬度的內力，本次建模取1m寬度單元內力。

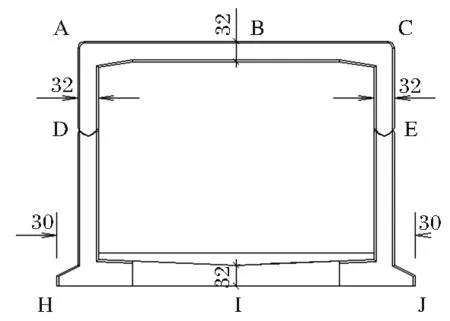
圖3 結構驗算位置示意圖

2 數值模擬結果分析

2.1 計算數據

(1)覆土壓力p恒=Kγ1H=1.545×18×4=111.24kN/m2；

(2)側土壓力p側1=γ1Htan2(45°-φ/2)=4×18×0.333=24.00kN/m2；

p側1=γ1(H+h)tan2(45°-φ/2)=18×(4+3.28)×0.333=43.64kN/m2；

(3)車輛荷載垂直壓力q車=∑G/(a×b)=8.90kN/m2；

(4)活載土壓力p活側=q車×tan2(45°-φ/2)=8.90×0.333=2.97kN/m2。

2.2 模型內力

箱涵在多種組合下的彎矩圖、軸力圖見4～圖9。

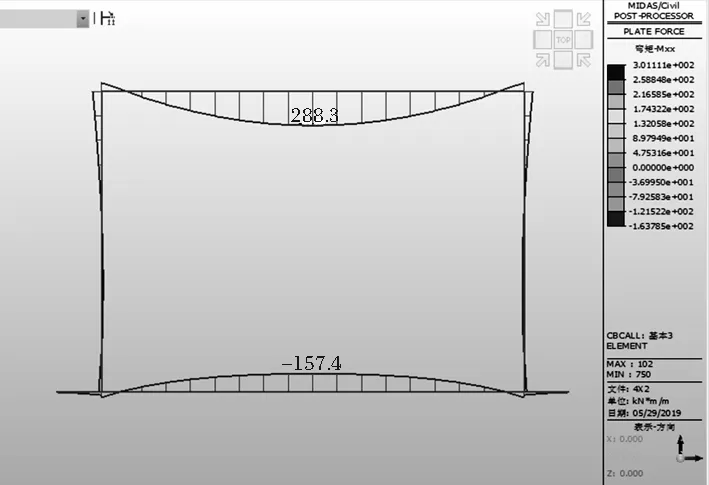
圖4 箱涵在基本組合下的彎矩圖

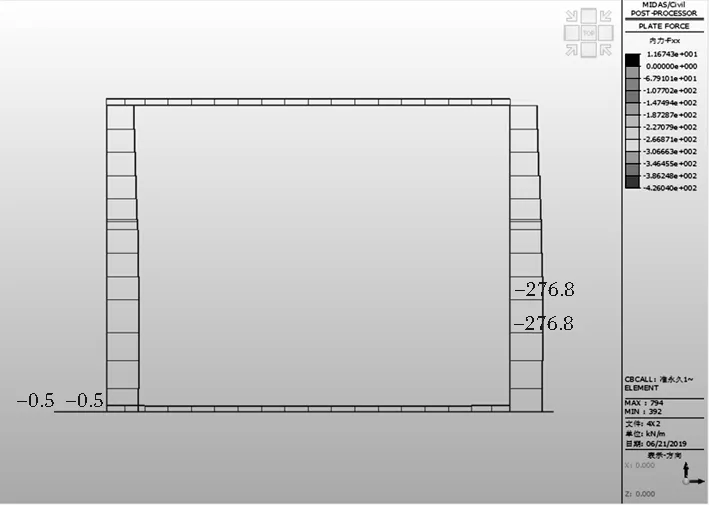
圖9 箱涵在準永久組合下的軸力圖

2.3 結果分析

計算結果見表1。通過對數據分析整理可以看出，計算結果均滿足承載能力極限狀態正截面抗壓、承載能力極限狀態斜截面抗剪、正常使用狀態截面抗裂驗算。

表1 結果分析

3 結論

采用有限元軟件對預制裝配式箱涵進行模擬分析，得出在承載能力極限狀態以及正常使用極限狀態下均滿足受力要求。

預制裝配式涵洞在實際應用中確實體現了較為明顯的優勢，隨著預制裝配式涵洞施工方法的普及，在越來越多的高速公路修建中應用也是未來交通建造行業發展的必然。但是還需要對預制裝配式涵洞在不同環境下的安全性進行研究評估，必須要嚴格對預制涵洞的施工進行計算，從而有效提升預制涵洞在實際工程中的應用范圍。