軸承套圈磨削加工誤差傳遞半參數模型及分析

王曉菲，李 航，彭 程，李楊龍

(河南科技大學 機電工程學院，河南 洛陽 471003)

0 引言

現代工業的迅速發展對精密軸承質量的要求越來越高[1]，軸承行業迫切需要科學合理的方法提高軸承零件的精度以及軸承生產線的產能。大部分產品質量問題來自制造過程[2]，因此質量控制的對象應從最終成品轉向加工過程，通過對加工過程各個環節產品的實時檢測和加工工藝的動態調整，來實現影響質量因素的監測分析以及加工工藝的優化，進而達到控制產品質量的目的。

在機械加工中，隨著加工工序的順延，加工誤差有序地流過從毛坯到零件的各個加工工序，這個誤差流動的過程即誤差流。近年來，眾多學者針對誤差流進行了深入的研究。文獻[3]提出了誤差流理論，同時在車身裝配過程中得到了應用和驗證。文獻[4-5]通過跟蹤和測量加工過程中各個階段的單個零件的特征尺寸，研究離散零件在多階段生產過程中的關鍵特征尺寸變化，并確定對最終產品的誤差影響最大的階段。文獻[6]根據最終產品的誤差是由所有工序誤差的累積和疊加產生，提出了一種狀態空間模型及其建模策略，建立了裝配和加工過程的運動學模型。文獻[7]引入了機器人領域微分運動矢量的概念作為工件集合偏差的狀態向量，并建立了通過狀態轉移來定量描述誤差的累積和轉換的狀態空間模型。

文獻[8-9]提出了加工誤差流的理念，并借助誤差理論、迭代映射、突變論以及神經網絡等理論，構造了多個加工誤差流動態模型。文獻[10-11]依據灰色系統理論和軸承磨削加工的誤差特點，建立了動態分析模型，擬合精度和預測效果相比傳統離散模型得到較大提升。文獻[12-13]參考誤差流理論，將多工序間的誤差傳遞過程表示為狀態空間方程，建立誤差傳遞模型，有效地反映了制動鉗加工過程中的誤差傳遞規律。文獻[14]將零件加工過程看作刀具軌跡點集與零件點集的轉換過程，將點集表示為齊次坐標矩陣，該矩陣包含了制造過程中的幾何變動信息，從而可以分析誤差傳遞規律。

上述對誤差流的研究尚處在建立線性模型階段，且主要集中在裝配過程中以零件的誤差為組成環的誤差累積的情況，較少考慮同一表面經過多次加工的工序間誤差傳遞。但是在實際的加工過程中，誤差的出現隨機性較大，并非全都是線性的。本文考慮上一道工序誤差對本道工序誤差的影響，以及本道工序的系統誤差和隨機誤差，建立了半參數回歸模型，利用自然樣條最小二乘法對模型中的參數及半參數進行求解，并以軸承套圈的內圈溝道加工作為實例，驗證了模型的可行性和優越性。

1 加工誤差傳遞模型

磨削加工是軸承內圈加工的核心步驟，本文以軸承內圈的磨削加工過程為例，進行工序間誤差傳遞的研究并建立半參數模型。為方便研究軸承內圈加工過程中各工序誤差對產品質量的影響，將其加工過程表示為如圖1所示。

圖1 軸承套圈多工序加工過程示意圖

圖1中：xi-1是工序i的輸入誤差，xi是工序i的輸出誤差，si是工序i的系統誤差，di是工序i的隨機誤差。在具有N個工序的軸承套圈加工過程中，將加工過程看作一維離散時變系統，工序i-1的輸出尺寸xi-1是工序i的輸入尺寸，工序i的輸出尺寸為xi。設xi-1和xi之間的關系為：

xi=f(xi-1)+si+di，

(1)

xi=f(xi-1)+si(t)+di。

(2)

若以xi-1,0表示尺寸xi-1的基本尺寸，在xi-1-xi-1,0處對f(xi-1)泰勒展開，得：

(3)

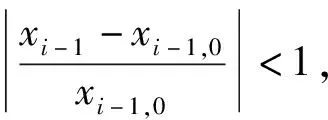
f(xi-1)=f(xi-1,0)+f′(xi-1,0)(xi-1,0-xi-1)。

(4)

將式(4)代入式(3)，得到：

xi-f(xi-1,0)=f′(xi-1,0)(xi-1-xi-1,0)+si(t)+di。

(5)

但是實際加工過程中，為了保證所有產品的最大合格率即零件的最終尺寸在允許的公差范圍內的概率最大，最后一次的切削加工并未按照圖紙中的尺寸進行，而是按照圖紙中的中差尺寸加工，若以xi,0表示工序i的設定工藝尺寸，則f(xi-1,0)≠xi,0。故假設：

(6)

將式(6)代入式(5)，得到：

(7)

令yi=xi-xi,0,βi=f′(xi-1,0)，則式(7)可化簡為：

(8)

式(8)為單個特征尺寸的多工序誤差模型。其中,βi(i=1,2，…，N)表示輸入誤差對輸出誤差的傳遞關系。

yi=βiyi-1+si(t)+di。

(9)

若在第i道工序上需要統計n個加工零件的m個重要特征尺寸，由于一個零件對應一個系統誤差，因此n個加工零件對應有n個系統誤差，傳遞系數βi在每個特征尺寸上發生不同變化，共有m個傳遞系數，由式(9)可得：

yi,j,k=βi,kyi-1,j,k+si(tj)+di,j,

(10)

其中：j=1,2，…，n；k=1,2，…，m。

將式(10)表示為矩陣形式，則為：

(11)

令

S=(si(t1)si(t2) …si(tn))T；

Δ=(di,1di,2…di,n)T，

則可以將式(11)寫為半參數模型：

L=BX+S+Δ。

(12)

2 基于自然樣條補償最小二乘參數估計

2.1 半參數模型參數估計

由半參數回歸模型(12)，可得誤差方程式為：

(13)

VTPV=min，

(14)

其中：P為對稱正定方陣，是觀測值L的權。方程系數矩陣半正定不可逆，所以方程的解并不是唯一的，修改平差準則使得方程有且僅有一個解，使用補償最小二乘原則[15]：

(15)

自然樣條函數半參數估計應滿足如下極值條件[18]：

(16)

多個樣條互相彎曲連接后沿其邊緣畫出的曲線就是三次樣條曲線，由于其插值結果的光滑程度最好，所以可由第二項來刻畫s(t)的光滑程度。

由補償最小二乘原理的補償項可以表示為：

(17)

其中：S=(s(t1),…,s(tn))T；R=QT-1QT，Q與T是n×(n-2)與(n-2)×(n-2)維帶狀矩陣。令hi=ti+1-ti,i=1,2, …,n-1，則Q矩陣元素qij滿足：

qij=0,|i-j|≥2。

T矩陣元素tij滿足：

tii=(hi+hi+1)/3,i=1,…,n-2；

qi,j+1=hi+1/6,i=1,…,n-3；

qi,j-1=hi/6,i=2,…,n-2；

tij=0,|i-j|≥2。

根據補償最小二乘原理，由式(15)按照求條件極值的拉格朗日(Lagrange)函數法，構造拉格朗日函數：

(18)

K=PV；

(19)

(20)

BTK=0。

(21)

將上述公式中的式(19)代入式(21)，并兼顧式(13)可以得到：

(22)

將式(19)代入式(20)，考慮式(13)，得到：

(23)

由式(22)和式(23)得到法方程：

(24)

法方程滿足rank(QTB)=t時，法方程的系數矩陣是可逆的，此時所求解的方程有唯一解。構造二次型：

(25)

顯然，二次型f≥0，已知矩陣P和T-1是正定矩陣，所以當且僅當

(26)

(27)

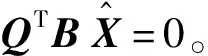
根據式(24)可計算得到迭代求解方程如下：

(28)

(29)

將式(28)代入式(29)并令

M=(P+αR)-1P，

(30)

則有：

(31)

其中：I是n×n階單位矩陣。式(31)被稱之為廣義最小二乘方程，其解如下：

(32)

(33)

其中：H(α)是帽子矩陣，即：

H(α)=M+(I-M)B(BTP(I-M)B)-1BTP(I-M)。

(34)

2.2 光滑參數α的確定

在半參數模型中，所求解參數的擬合程度與光滑程度之間的平衡受到α取值的影響，在選取合適的R后，α的取值對計算結果有較大影響。為了計算方便，通常采用廣義交叉核實函數計算[19-20]：

(35)

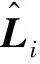
3 試驗驗證

為檢驗半參數模型是否適用于軸承套圈加工過程中的誤差分析，試驗選取某工廠某型號軸承內圈加工數據為研究對象，建立了半參數模型，通過計算殘差、均方誤差和平均絕對誤差檢驗半參數模型。同時，建立參數模型并將半參數模型與參數模型進行對比，驗證半參數模型的預測效果。

3.1 試驗數據及模型求解

按照加工順序在生產線上選取140個軸承內圈，并按1～140的序號編號，分別測量溝道的粗磨、精磨誤差作為本次試驗數據，所測量的粗磨誤差和精磨誤差原始數據分別如圖2和圖3所示。

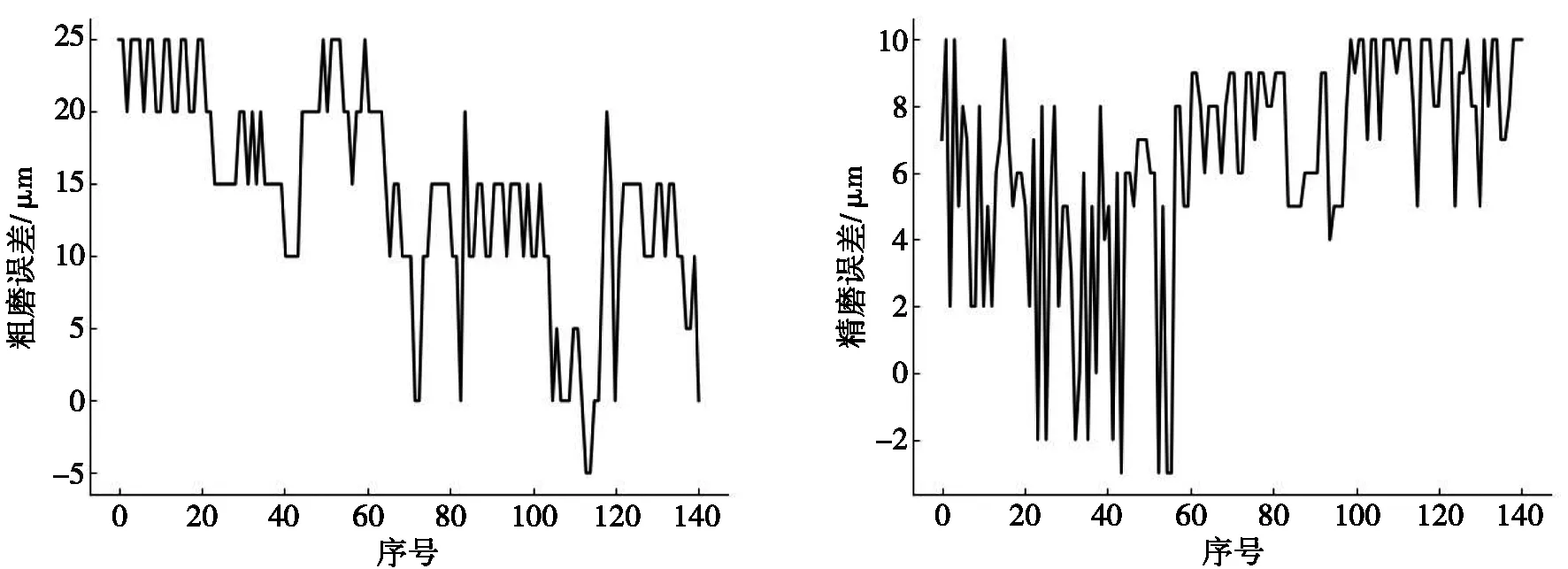
圖2 粗磨誤差原始數據 圖3 精磨誤差原始數據

選取序號為1～100的數據作為樣本點，建立半參數模型L=BX+S+Δ和參數模型L=BX+Δ。由樣本點100組數據，根據上述參數估計方法求解兩模型中的參數。在參數模型中根據最小二乘法求解的模型參數X=0.352 3。在半參數模型中，由廣義交叉核實函數法計算并選取最優點α=0.3，由式(32)計算可得模型參數X=0.047 4，由自然樣條最小二乘法估計粗磨工序至精磨工序的系統誤差S。

3.2 模型檢驗及分析

選取序號101～140的40組數據作為檢驗點，由上述所求解的半參數模型和參數模型分別計算檢驗點的預估值，并將預估值與實測值進行比較計算殘差。參數模型和半參數模型的樣本點殘差對比和檢驗點殘差對比分別如圖4和圖5所示。

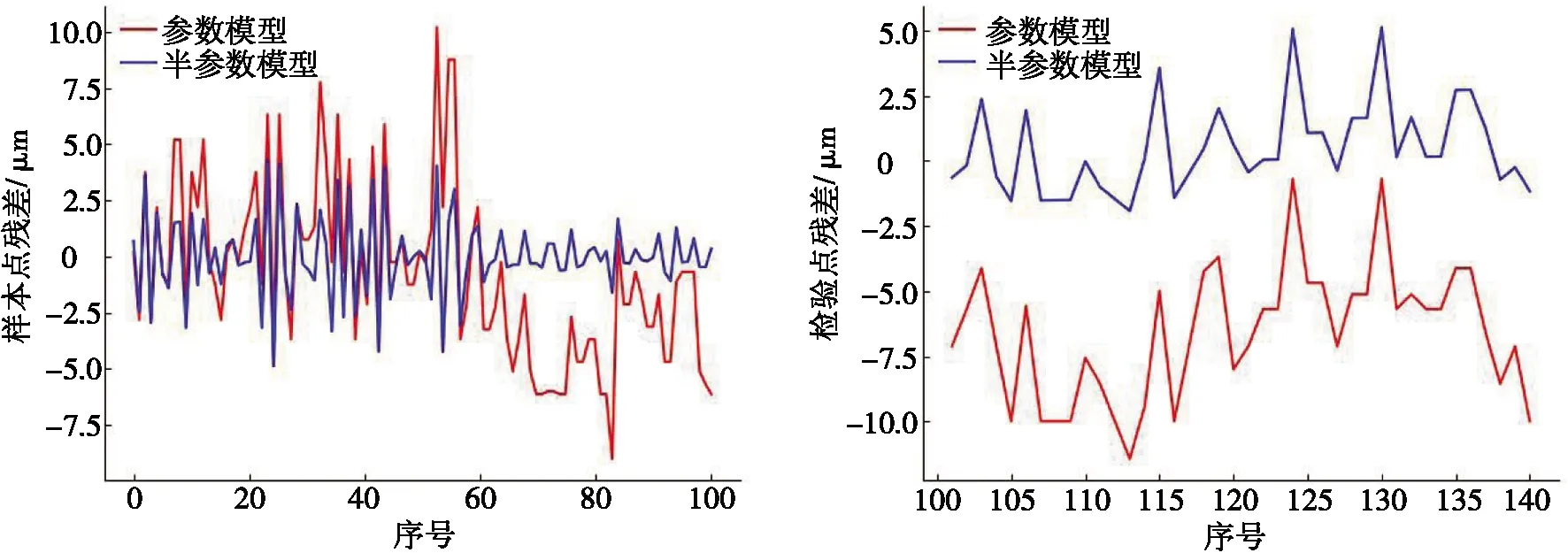
圖4 樣本點殘差對比 圖5 檢驗點殘差對比

由圖4和圖5可知：相對于參數模型，半參數模型的殘差點比較均勻地落在水平的帶狀區域中，且帶狀區寬度較窄，說明半參數的擬合精度更高。

根據預測值的殘差，分別計算參數模型和半參數模型的均方誤差和平均絕對誤差，其結果如表1所示。

表1 擬合誤差對比

由表1可知：與參數模型相比，半參數模型的均方誤差從49.78降低到3.18，平均絕對誤差從6.60降低到1.31，均遠遠小于參數模型，因此半參數模型的擬合效果更好。

4 結論

針對軸承內圈制造過程中的誤差分析建立半參數模型，可以求解出體現工序間誤差影響關系的傳遞系數X，傳遞系數X表明了上一道工序的加工誤差對本道工序加工誤差的影響程度。將半參數模型與參數模型相比，半參數模型的殘差、均方誤差和平均絕對誤差均遠遠小于參數模型，因此半參數模型精度更高，擬合效果更好。