煤炭自動定量裝車控制策略設計

齊世煒，孫 暢，付主木, b，李 玲，陶發展, b，司鵬舉, b

(河南科技大學 a.信息工程學院；b.河南省機器人與智能系統重點實驗室；c.國際教育學院，河南 洛陽 471023)

0 引言

煤炭是中國的基礎能源和重要原料，在國民經濟中占有重要的戰略地位[1]。在煤炭裝車環節方面，傳統人工裝車模式由于中間人工環節繁雜，經常出現車輛滯留、通行緩慢等現象[2]。因此，為了提高裝車精度與效率，亟需開發煤炭快速定量裝車自動控制系統。

近幾年，中國對自動裝車系統的研究逐漸興起[3]。文獻[4]借鑒高速公路電子不停車收費(electronic toll collection, ETC)系統，設計了面向礦山的全自動車輛識別系統、自動稱質量系統和自動連續裝車系統，但缺乏較為先進的控制算法。文獻[5]提出了基于內模原理的比例-積分-微分(proportional integral differential, PID)控制算法，依靠可編程邏輯控制器(programmable logic controller, PLC)控制技術實現給煤設備控制、牽引列車速度控制與裝車計量檢測，但當模型不匹配時容易出現問題。文獻[6]設計了全自動火車煤礦裝車系統，重點研究了自動裝車的伺服控制系統，提高了裝車精度，但伺服系統中的調節器采用傳統的PID調節器，無法實現PID參數的自適應整定[7-9]。文獻[10]針對定量裝車提出了混合控制技術，采用定量粗裝、衡量和精確添加的分層控制策略，極大地提高了裝車精度，但在實際應用中較為復雜。綜上所述，目前的煤炭自動定量裝車控制系統要么缺乏較為先進的控制策略，要么控制策略相對簡單難以應對復雜多變的客觀情況或控制策略在實際應用中較為復雜。因此，本文提出了一種基于模糊推理的PID參數自適應整定控制系統。針對控制系統建立數學模型，實現系統的模糊PID控制方法并設計模糊控制器。對控制系統中存在影響系統性能的環節提出補償策略，并進行仿真驗證及試驗測試。

1 控制系統組成與特性

1.1 控制系統組成

本煤炭自動定量裝車控制系統由給煤倉給料系統、計量帶式稱質量給煤系統、液壓閘門控制系統、電氣控制系統、傳感器檢測系統等子系統組成。控制系統核心部分為給煤倉給料系統，給煤環節決定裝車系統的裝載精度。實現快速精準裝車，關鍵部分也在給煤環節。本文所設計的給煤倉給料系統示意圖如圖1所示，給料口由液壓閘門的開閉控制給料的啟停，液壓閘門的開啟狀態決定瞬時給煤量的多少。當煤炭從給料口放出，落至計量帶式稱質量給煤機上進行稱質量，煤炭經過稱質量給煤機運送至緩沖倉，落入裝載車廂，完成動態稱質量裝車。

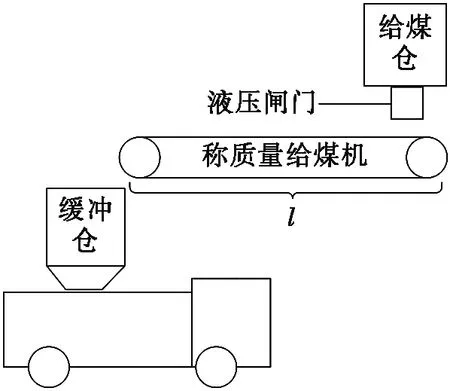
圖1 給煤倉給料系統示意圖

1.2 控制系統特性

控制系統核心被控對象為放料閘門，在放料閘門給煤過程中可近似視為自平衡單容過程。此過程可用一階慣性環節[11]描述為：

(1)

其中：K為過程的放大系數；T為過程的時間常數；s為時域函數拉普拉斯變換下的復參數。

在皮帶傳輸煤炭裝車過程中，煤炭要經過長度為l的帶式稱質量給煤機，經時間τ后才進入車廂，此過程為純滯后過程，可用一階時滯環節[11]描述為：

G2(s)=e-τs,

(2)

其中：τ為過程的純滯后時間。

因此，整個給煤裝車環節可描述為：

(3)

對于本文控制系統，K=3，T=1.1，τ=0.3。

2 模糊PID控制

2.1 模糊PID控制實現原理

煤炭自動定量裝車要求在盡可能短的時間內完成精準給料，實現這一過程的關鍵環節在于對給煤倉閘門的有效控制[12]。以閘門的開度為控制依據，設裝車過程中給煤倉的瞬時給煤量(閘門開度)為P(t)，傳感器檢測到的煤堆實時高度為h(t)，期望高度為H，H與h(t)之差記為δ(t)。

經多次測試可以得出接近真實值的裝煤密度ρ，裝車前激光雷達檢測出車廂的長和寬分別為l和w，假設目標裝車質量為M，則裝車的期望高度為：

(4)

由于一維模糊控制器只通過偏差值變化進行控制，很難反映實際使用過程中輸出變量的動態特性，在控制精度上難以達到滿意的效果。二維模糊控制器，輸入為偏差和偏差的變化率，因為其具有偏差的變化量，能夠更好地展現被控對象的動態特性，效果上優于一維模糊控制器[13]，故選用二維模糊控制器。基于以上分析可設計出如圖2所示的模糊PID控制系統，利用模糊推理，對控制系統的PID參數KP、KI、KD進行實時整定(整定值為ΔKP、ΔKI、ΔKD)。

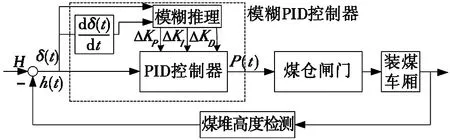
圖2 模糊PID控制系統原理圖

裝煤過程中，各時刻下料速度及下料量不同，則所需最優PID參數也不同。以期望高度與檢測煤位高度的偏差δ(t)、偏差的變化率δ(t)/d(t)作為二維模糊控制器輸入，閘門開度為輸出，在運行中不斷判斷δ(t)和δ(t)/d(t)的變化情況，運用模糊推理對3個參數進行自適應整定。

2.2 史密斯補償

由于控制系統中存在滯后環節，僅靠PID控制很難獲得良好的控制質量。時滯環節具有響應滯后的特點，這將導致系統需經過較長的調節時間并產生明顯的超調[14]。

由控制系統閉環傳遞函數可知：特征方程中含有時滯環節e-0.3s，這是導致常規PID控制下系統出現較大超調、振蕩的原因。史密斯補償算法可以實現對于純滯后對象的補償[15]，其基本思路為:在控制系統中增加環節或增加控制支路，使系統的控制通道以及系統傳遞函數的分母不含有純滯后環節[16]，從而改善控制系統的控制性能及穩定性。史密斯補償基本原理如圖3所示。圖3中：Gp(s)為增加補償環節后的等效補償函數；Gc(s)為PID調節器;g(s)為傳遞函數不含時滯的部分[17]。

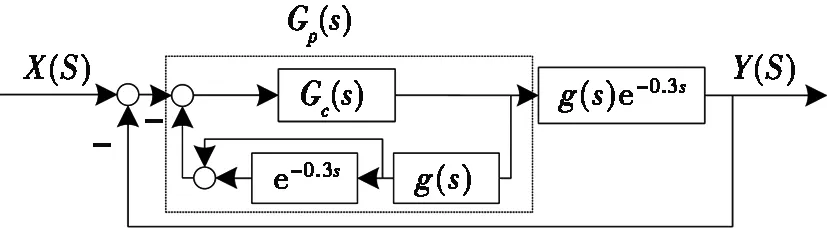
圖3 史密斯補償原理示意圖

由圖3可得等效補償函數為：

(5)

此時，系統閉環傳遞函數為：

(6)

將式(5)代入式(6)可得：

(7)

此傳遞函數特征方程不再含有時滯環節，從而將消除時滯環節對系統的影響。

2.3 模糊PID控制器設計

2.3.1 隸屬度函數選取

將模擬量系統誤差δ(t)、誤差變化率δ(t)/d(t)、系統控制變量u(t)離散化得到數字量，分別記為E(n)、D(n)和U(n)。將E(n)和D(n)作為二維模糊控制器的輸入[18]：

E(n)=S(n)-y(n),D(n)=E(n)-E(n-1)，

(8)

其中：S(n)為系統的理想輸出；y(n)為實際輸出。

模糊規則[19]為：

如果E(n)為正且D(n)為正，則ΔU(n)為正；如果E(n)為正且D(n)為負，則ΔU(n)為0；

如果E(n)為負且D(n)為正，則ΔU(n)為0；如果E(n)為負且D(n)為負，則ΔU(n)為負，

其中，ΔU(n)為控制器輸出的變化量。

對輸入輸出變量E(n)、D(n)和U(n)均采用對稱、均勻全交疊的三角形隸屬度函數[20]，為便于分析，把所有變量的論域設計為基本論域[-1,1]，并將此類模糊控制器稱為通用模糊控制器。在進入通用模糊控制器之前，將輸入信號E(n)、D(n)通過正規化因子GEi、GDi進行正規化變換轉換到基本論域上，模糊控制器輸出信號U(n)在輸入被控過程之前也必須通過正規化因子GU進行反正規化轉換到實際論域，即：

E*=GEiE(n),D*=GDiD(n),U(n)=GUU*，

(9)

其中：i=1，2且E*，D*，U*∈[-1,1]。

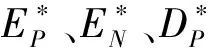
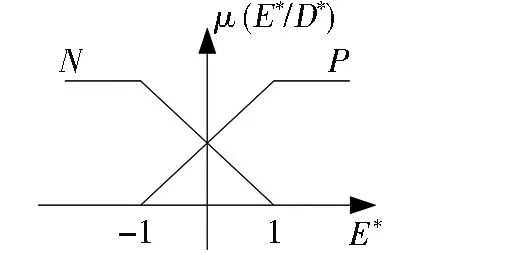
圖4 輸入變量的三角形隸屬度函數

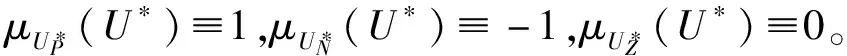
加權平均法解模糊公式為：

(10)

根據前文所述模糊規則，在任意時刻每條激活的規則為：

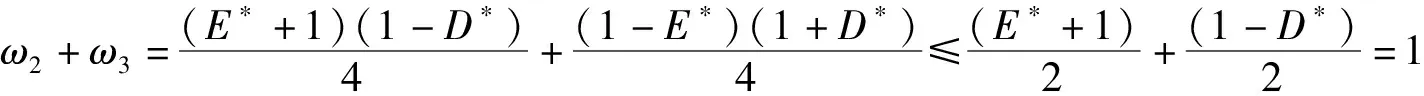
經模糊推理及解模糊可以得到：

經反正規化變換，可得：

則全局模糊PID控制器輸出為：

數字PID控制算法公式為：

(11)

對比各項系數可得模糊整定參數為：

則修正后的PID參數為：

KP=KP0+ΔKP,KI=KI0+ΔKI,KD=KD0+ΔKD。

2.3.2 模糊規則表制定

針對不同情況下的料高，將料高偏差E、料高偏差變化率D的論域劃分為[0, 6]，對不同的料高偏差E及偏差變化率D采用ZO(零)、SS(小小)、SB(小大)、MS(中小)、M(中)、BS(大小)、BB(大大)描述，其含義為檢測料高與期望料高偏差E從小到大，對應料高偏差D的變化率由慢到快。即論域等級E=D=[0, 1, 2, 3, 4, 5, 6]，對應的模糊子集E=D=[ZO, SS, SB, MS, M, BS, BB]。

根據工程實踐經驗及PLC參數整定設置試驗，KP的最佳取值范圍為[0.2, 1.6]，KI的最佳取值范圍為[0.1, 1.0]，KD的最佳取值范圍為[0.02, 0.1]。取PID參數的初值KP0=0.08，KI0=0.03，KD0=0.01。將ΔKP、ΔKI、ΔKD的論域同樣劃分為[0, 6]，即ΔKP=ΔKI=ΔKD=[0, 1, 2, 3, 4, 5, 6]，對應的模糊子集ΔKP=ΔKI=ΔKD=[ZO, SS, SB, MS, M, BS, BB]，量化因子取K(ΔKP)=0.2，K(ΔKI)=0.1，K(ΔKD)=0.005。

模糊化處理后，制定模糊規則進行模糊推理。通常考慮以下情況：

(Ⅰ)當偏差E較大時，系統處于響應階段，此時誤差變化率D變化較快，為了使動態響應快，KP應較大；但為了避免積分飽和，出現較大的超調量，應限制積分強度，可令KI=0；同時，為防止微分飽和，KD不宜太大。

(Ⅱ)當偏差E大小處于中間位置，系統處于上升階段，誤差變化率D變化適中，此時KP、KI、KD應取值適中，盡量防止超調，同時還需兼顧系統的動態響應。

(Ⅲ)當偏差E較小時，系統處于微調階段，誤差變化率D變化較快，為得到較好的穩態性能，應適量增大KP、KI；同時為了防止振蕩，在偏差E未進入較小可接受范圍前，應適當加大KD，以使系統快速穩定，之后，可適量減小KD，以保證系統的穩定性。

根據以上分析，針對不同情況的料高偏差E(n)、偏差變化率D(n)，可分別建立KP、KI、KD的模糊控制規則，見表1。

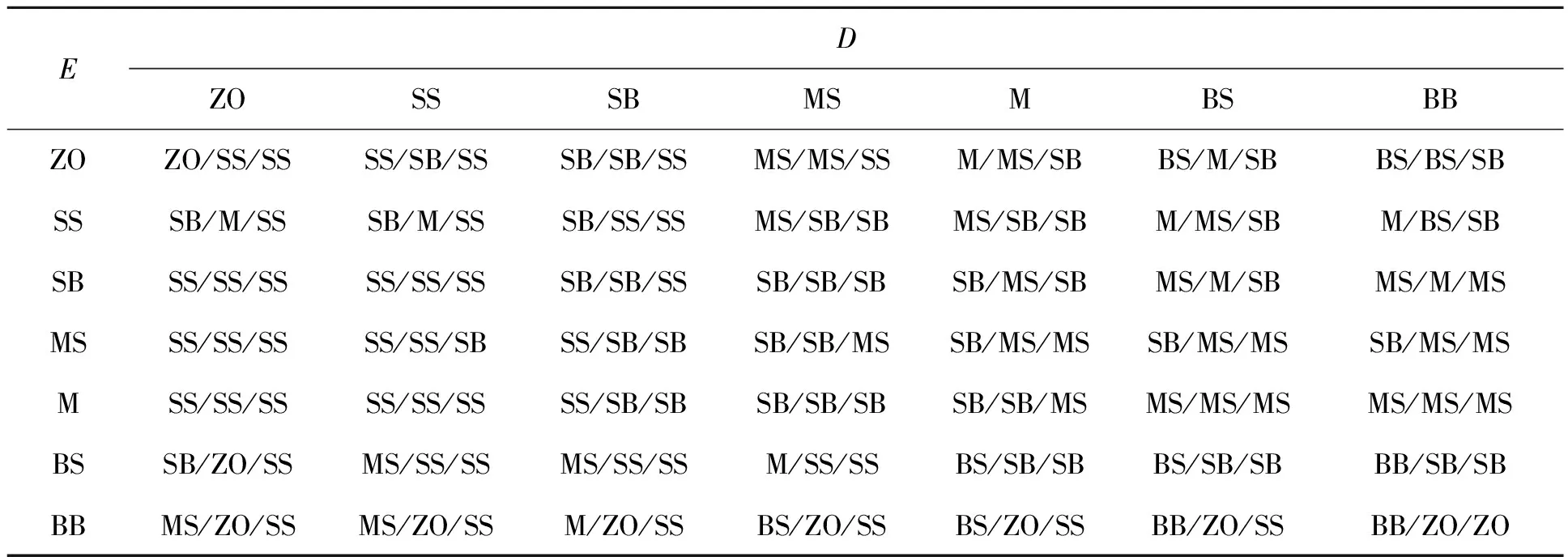
表1 KP、KI、KD模糊規則

3 仿真分析與試驗測試

在MATLAB/SIMULINK軟件中建立系統仿真模型，對系統動態特性及穩態特性進行仿真分析。選用模糊PID控制算法模擬裝車過程，并選擇常規PID控制算法作為對比，通過仿真對比分析控制系統在簡單閉環比例控制、常規PID控制、模糊PID控制下對階躍信號的跟蹤情況，進一步在試驗平臺進行測試。

3.1 系統性能仿真分析

3.1.1 無史密斯補償下系統性能仿真分析

在閉環比例控制、常規PID控制、模糊PID控制下，通過仿真測試控制系統對階躍響應的跟蹤狀況進行系統性能分析。向控制系統輸入階躍信號，系統在閉環比例控制、常規PID、模糊PID控制算法下的階躍響應如圖5所示。仿真過程中模糊控制器在不同時刻整定出的ΔKP值如圖6所示。

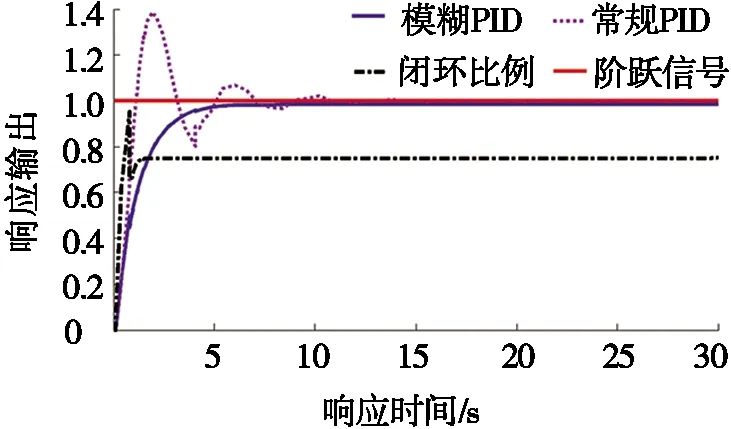
圖5 無史密斯補償下不同控制算法階躍響應

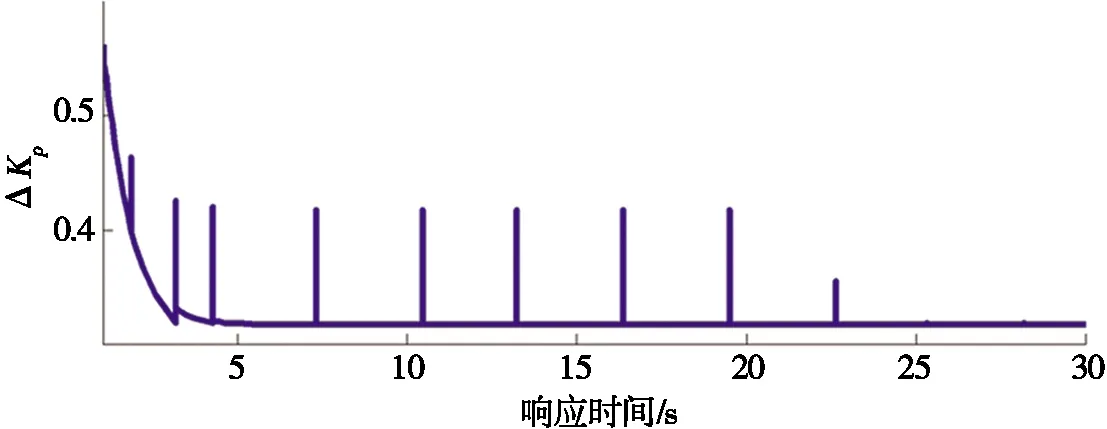
圖6 無史密斯補償下模糊整定ΔKP值

由圖5可以看出：閉環比例控制在響應前期存在較大跳變且存在較大穩態誤差；常規PID控制下，系統響應前期存在較大(約40%)的超調并且調節時間較長(約10 s)；而模糊PID調節時間較短(約5 s)且無超調量。但由圖6可以看出：模糊控制器整定出的ΔKP值存在頻繁跳變。

3.1.2 史密斯補償下系統性能仿真分析

加入史密斯補償環節后，閉環比例控制、常規PID控制、模糊PID控制下的階躍響應如圖7所示。仿真過程中模糊控制器在不同時刻整定出的ΔKP值如圖8所示。

圖7 史密斯補償下不同控制算法階躍響應

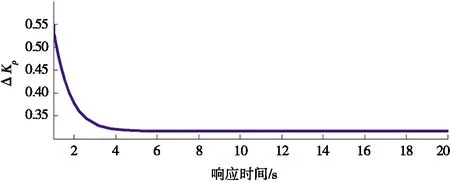
圖8 史密斯補償下模糊整定ΔKP值

由圖7可以看出：加入史密斯補償環節后，閉環比例控制在響應前期不再出現劇烈跳變，但依舊存在著較大的穩態誤差。常規PID控制下，系統超調量明顯減小(約為20%)，系統調節時間也減少了6 s左右；而模糊PID控制下，不存在超調，調節時間也更短(4 s左右)，系統性能得到改善。由圖8可以看出：加入史密斯補償環節后，模糊整定出的ΔKP不再出現跳變。

3.2 控制系統模擬裝載仿真分析

由3.1.2節分析可知：閉環比例控制下，系統存在較大跟蹤誤差，模糊PID控制較常規PID控制具有更好的響應特性，采用模糊PID控制算法模擬裝載過程并用常規PID控制作為對比。假設某次裝車目標裝載量為500 kg，常規PID和模糊PID控制下的裝車模擬質量變化曲線如圖9所示。

由圖9可以看出：模糊PID控制算法下，1.8 s即達到目標裝載質量的80%，而常規PID控制下，2.1 s左右才達到該裝載質量；并且常規PID控制下起始階段存在明顯的遲滯，而模糊PID控制算法下，整個裝載過程都更為流暢，反應更迅速靈敏。模糊PID控制算法較常規PID更穩定，響應速度更快。

圖9 裝車模擬仿真質量變化曲線

3.3 試驗平臺測試

在試驗平臺進行裝車測試，目標裝載質量為500 kg，多次測試取平均值。裝車試驗測試質量變化曲線如圖10所示。由圖10可知：常規PID控制算法下，4 s以前系統響應較遲滯，10 s達到目標裝載質量；模糊PID控制下，系統響應較迅速，8.5 s達到目標裝載質量。模糊PID控制較常規PID控制的裝載時間縮短了15%。常規PID控制的平均裝載質量為498.6 kg，模糊PID控制的平均裝載質量為499.2 kg。常規PID控制的裝車誤差為0.28%，模糊PID控制的裝車誤差為0.16%，裝車誤差降低了42.86%。模糊PID控制較常規PID控制反應速度更快，裝載誤差更小，模糊PID更能滿足行業對裝載快速性及準確性的要求。

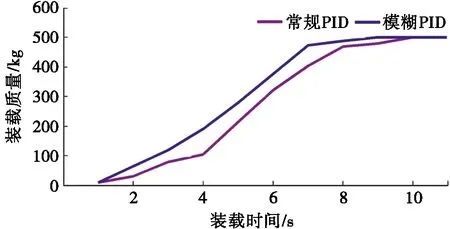
圖10 裝車試驗測試質量變化曲線

4 結論

(1)采用模糊PID控制算法使得控制系統的控制參數得到了優化，控制系統的快速性和穩定性得到了明顯提高。裝車的速度提高了15%，裝車精度提高了42.86%。

(2)采用史密斯補償，彌補了時滯環節對系統響應造成的影響，提高了系統響應的穩定性和快速性。常規PID控制下，超調量減小了約50%，調節時間縮短了約60%，模糊PID控制下調節時間縮短了20%左右。