氣動液壓錘錘擊系統建模與分析

訚耀保, 喻展祥, 李文頂, 林 登, 郭傳新

(1.同濟大學 機械與能源工程學院, 上海 200092; 2.上海航天控制技術研究所, 上海 201109; 3.浙江永安工程機械有限公司, 浙江 溫州 325204;4.北京建筑機械化研究院, 北京 100007)

引言

樁是一種設置在土體中豎直或傾斜的傳力構件，能夠將來自地面建筑的全部或部分載荷傳遞到較深和較強的土層中去，具有承載力大、抗震性能好、適應性強等特點。據估計，樁基礎工程占建筑基礎總工程的1/2～2/3[1]，而建設樁基礎的關鍵在于沉樁。錘擊沉樁方式以其工藝簡單、打擊能量高、使用成本低等優點在現代樁基施工工程中占很大比重[2]。錘擊沉樁設備主要包括柴油錘和液壓錘，隨著近年來人們開始追求以高效、環保和可持續為目標的綠色發展理念，柴油錘因在施工時存在噪聲大、油煙污染嚴重和打樁效率低等問題，已經在許多國家和地區被限制使用。相對而言，液壓錘不僅不存在環保方面的問題，還具有打樁能量高、施工適應性強、可實現打斜樁和水下打樁等優點，因此在打樁設備市場上液壓錘有逐漸取代柴油錘的趨勢[3-4]。

在沉樁之前往往需要對可打入性進行分析，因此涉及沉樁設備元件進行合理的選型與匹配以保證沉樁過程的經濟性和高效性，同時要避免在沉樁過程中出現截樁、樁身壓潰和樁頭損壞等現象[5]。為此，在給定的錘-樁-土系統的情況下對沉樁能力進行分析至關重要。國內外關于沉樁動力學方面的研究主要經歷了2個階段[6]：早期主要是基于牛頓碰撞理論，將兩相撞擊的錘與樁均視為剛體，即不考慮其具體的結構與形狀，忽略了沖擊能量在系統各部件之間的傳遞過程，由此雖可以快速求解出沉樁過程的動力學響應，但無法考慮系統各部件參數對沉樁過程的具體影響，各部件間匹配關系的優化也缺少理論上的支撐。此外基于碰撞理論而建立的動力學模型無法清楚地解釋實際工程中出現的相同打擊能量時“重錘輕擊”優于“輕錘重擊”的現象。基于古典碰撞理論建立的打樁公式在實際工程中表現出了很大局限性，現代樁錘設計計算必須以波動理論為基礎[7-8]。將應力波理論應用于沉樁過程的研究已經有很長的歷史，早在19世紀VENANT S就研究了剛性錘與無限長彈性桿的撞擊問題[9]。ISAACS DV首先提出打樁過程是應力波在包括樁錘與樁的系統內的傳播過程，建立了經典的一維波動方程[10]。SMITH以無質量彈簧與剛性質量塊分別考慮了樁錘、墊層以及樁身各部分的彈性與質量，提出了基于一維波動理論的打樁公式[11]。本研究基于波動力學的基本理論，對沉樁系統各部件間的相互作用進行了動力學分析，建立了錘、墊層和樁三者間的作用模型，推導出了沉樁過程中錘擊力的解析解，并應用其從理論上解釋了工程中出現的“重錘輕擊”優于“輕錘重擊”現象，分析了墊層剛度對錘擊力的影響，最后分別針對兩種土體介質模型建立了錘-樁-土系統的動力學方程。

1 氣動液壓錘的工作過程

氣動液壓錘是一種雙作用液壓錘，采用的是單出桿式氣體儲能控制油缸，其工作原理如圖1所示，控制油缸的無桿腔作為氣體室，工作時需充入一定初始壓力的氮氣，活塞下部為有桿腔，是液壓油的工作腔，錘芯通過連接機構與活塞桿相連。在液壓錘回程階段，進油控制閥打開，回油控制閥關閉，由泵站和高壓蓄能器向控制油缸下腔充入高壓油以推動活塞并拖動錘芯向上抬升，同時對氣體室中的氮氣進行壓縮做功。當錘芯上升到指定高度或氣體室中的氮氣達到設定壓力時，進油控制閥關閉，系統停止向控制油缸下腔供油，錘芯由于慣性會繼續向上運動一段距離，但在重力與氮氣壓力的共同作用下錘芯的速度迅速降為0，此時回程階段結束，在整個過程中系統的液壓能轉化為錘芯的重力勢能和氣體的壓力能。隨后回油控制閥打開，液壓錘進入沖程階段，控制油缸下腔開始向油箱和低壓蓄能器中泄油，錘芯加速向下運動直到與樁發生撞擊，至此液壓錘沖程階段結束，在這一過程中錘芯的重力勢能和氣體的壓力能轉化為錘芯的動能。撞擊過程結束后，液壓錘將進入新的工作循環。

圖1 氣動液壓錘工作原理圖

2 錘擊系統建模

如圖2所示，錘擊沉樁系統由樁錘、墊層(樁帽)、樁和巖土4部分組成[12]。液壓錘沖程階段結束時，錘芯以速度vh0沖擊墊層和樁，沖擊作用將使接觸界面上的質點產生擾動，根據波動力學的觀點，該擾動將在介質中以波的形式由近及遠的傳播，通常稱之為應力波。因此，樁貫入土體的過程實質上是應力波的產生和傳播過程[13]。一般地，錘芯的橫截面積較大，其波阻也較樁大很多，因此為簡化分析可以近似地將錘芯視為剛體，只考慮應力波沿樁身的傳播過程。對于一般的預制樁，其軸向尺寸遠遠大于徑向尺寸，因此在研究應力波在樁身中的傳播規律時，可以將樁簡化為一維細長桿，從而可以考慮應用一維縱波理論研究沉樁的過程。主要對錘擊力模型和樁-土間的相互作用模型進行分析。

圖2 沉樁分析示意模型

2.1 錘擊力模型

沉樁的錘擊力由錘芯對樁的沖擊作用產生，但并非是兩者的直接撞擊，實際工作時需要在錘與樁之間設置緩沖物即墊層。由于墊層的重量較錘和樁都小得多，因而可以忽略其慣性作用只考慮其受力與變形，本研究用無質量彈簧考慮其對錘擊力的影響，那么由樁錘、墊層和樁組成的沖擊系統模型如圖3所示。

圖3 沖擊系統模型

圖3中mh表示錘芯的質量，uh表示錘芯位移，up表示樁頂的位移，kc為墊層等效彈簧的剛度，F(t)為錘擊力。規定撞擊作用發生的時刻為t=0時刻。

撞擊過程中，對錘芯列動力平衡方程：

(1)

錘擊過程中錘芯位移等于墊層的壓縮量與樁頂位移之和，即滿足表達式：

(2)

將式(2)對時間t求二階導數后得到：

(3)

F(t)作用于樁頂，根據波動理論和材料的本構模型可以得到：

式中，Ep為樁的彈性模量；σp，εp分別為錘擊力作用下樁頂產生的應力和應變；c為應力波在樁身中傳播的速度。

將式(4)對時間t求二階導數后帶入式(3)，整理后再帶入式(1)將得到：

(5)

引入速度vp=?up/?t，對上式進行降階后得到：

(6)

當t=0時，錘芯速度為vh0，樁頂速度為0，即：

(7)

(8)

將式(2)對時間t求一階導數，并將式(7)與式(8)帶入可以得到當t=0時，滿足：

(9)

那么可以得到：

(10)

(11)

對式(11)進行Laplace反變換即可得到：

(12)

將式(12)帶入式(4)即可得到錘擊力的表達式：

(13)

由式(13)可知當t>π/ωd時,F(t)將出現負值，但由于墊層的等效彈簧不能提供拉力，因此可以認為F(t)的作用時間為0～π/ωd。另將F(t)對時間t求一階導數并令其等于0，可以求解出錘擊力的最大值Fmax與達到最大錘擊力所需的時間t*：

(14)

(15)

從錘擊力的表達式中還可以看出，影響錘擊力的因素主要是錘芯的質量、發生撞擊時錘芯的速度、墊層剛度以及樁身材料的屬性。圖4為不同墊層剛度時樁錘與樁撞擊產生的錘擊力F時間曲線，可以看出當墊層剛度較大時，通過墊層傳遞給樁的錘擊力也較大，相反若減小墊層的剛度，錘擊力會相應減小，同時撞擊力的持續時間會有所延長。因此，在實際沉樁時可以通過選擇合適的樁墊對錘擊力進行調整以保證沉樁過程的效率，同時也可以避免樁與樁錘的破壞。

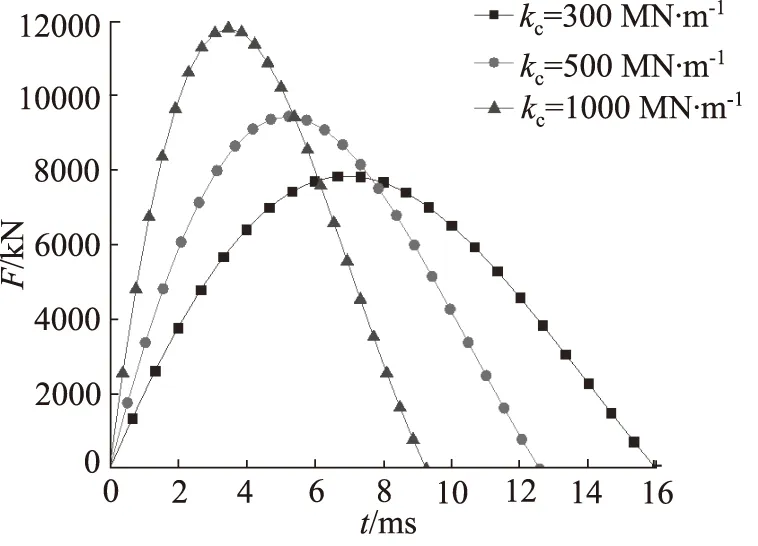
圖4 墊層剛度對錘擊力的影響曲線

樁錘與樁的撞擊過程是打樁能量由錘傳遞到樁的過程。對于氣動液壓錘來說，打樁能量來自液壓錘沖程階段錘芯重力和氣體室氮氣壓力對錘芯做的功，因此不同錘芯重量的液壓錘達到相同打樁能量時對樁的沖擊速度vh0不同，而錘芯重量和速度對錘擊力產生有直接影響。圖5是不同型號的液壓錘在打樁能量均為90 kJ時與樁撞擊而產生的錘擊力時間曲線。從圖像上可以看出，小質量錘沖擊產生的錘擊力峰值較大質量錘更高，錘擊力作用時間也較短，同時達到與大質量錘相當的打擊能量需要更大的工作行程。在實際工程中“輕錘重擊”容易產生過大的錘擊力從而損壞樁身和樁錘，同時從F-t曲線上可以看出輕錘沉樁產生的錘擊力對時間的積分即錘擊作用產生的沖擊能量更少。因此出于安全性和經濟性方面的考慮，應在能夠保證產生的錘擊應力足夠克服沉樁阻力的前提下適當增加錘重以“重錘輕擊”進行沉樁作業。

圖5 不同錘型的錘擊力時間響應

2.2 樁-土作用模型

樁與土的相互作用關系比較復雜，為簡化分析，本研究將樁簡化為一維均質彈性桿并對其作如下假設：沉樁過程中，樁的橫截面始終保持為平面，即樁身截面間的相互作用只考慮均勻分布的軸向應力； 忽略樁身的殘余變形，即認為樁的貫入度與樁頂的位移相等。錘擊力作為一個瞬態沖擊力施加于樁頂，將使撞擊界面上的質點產生擾動，該擾動將以應力波的形式沿樁身向下傳播，樁身質點將隨著應力波的傳播作軸向運動且服從一維波動方程式(16):

(16)

式中,R—— 土阻力項

x—— 樁身截面的位置坐標

u——x處截面上質點的位移

E，ρ—— 分別表示樁的彈性模量和樁身材料的質量密度

沉樁的過程是樁身質點在錘擊力的作用下克服土體阻力不斷貫入土體的過程，土阻力分布在沉入土層中的樁身周圍和樁身底部，在研究中為了使問題簡化，將土阻力全部移至樁底，并忽略樁周土阻力對應力波波形的影響。土阻力R包括與樁土相對位移有關的靜阻力Rs和與樁土相對運動速度有關的動阻力Rd。樁土之間的相互作用可以用如圖6所示的模型表示。本研究考慮靜阻力為理想彈塑性模型，其與樁身質點位移u的關系如圖7a所示，動阻力如圖7b與樁身質點的速度成正比。圖中u0為樁端土的最大彈性變形量，R0為土的極限靜阻力，cs為阻尼系數。

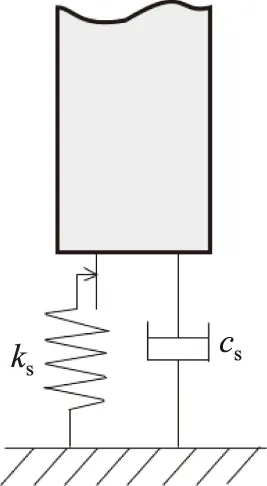
圖6 樁土作用模型

圖7 土阻力模型

因此土阻力可以表示為：

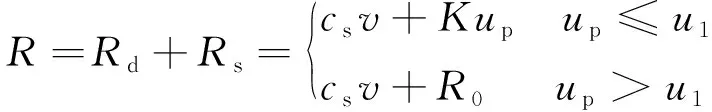
(17)

2.3 錘-樁-土系統的動態響應

樁錘沖擊樁產生的錘擊力以應力波的形式在樁身中傳播，當時間t=lp/c時，應力波傳到樁底，考慮波在樁底截面上的反射，并根據一維波動理論，此時系統的波動方程可以描述為：

(18)

式中,P與Q分別表示在樁身中傳播的下行波與上行波，對于樁底截面位置，P與Q均為時間的函數；v′與v″分別表示上行波與下行波對應的質點運動速度；v為樁身質點的實際運動速度；Zp=EpAp/c為樁的波阻抗。

為簡化分析，僅考慮應力波傳播到樁底的第一次反射情況，即不考慮經樁底反射的上行波對錘擊力下行波的影響，那么沉樁系統的波動方程中下行波P即是錘擊力波F(t)。下面將應用一維波動理論分別對由剛性錘、彈性樁與黏彈性土組成的系統和由剛性錘、彈性樁與黏塑性土組成的系統進行沉樁過程的動力學分析。規定系統中壓縮波為正值，質點速度的正方向向下，所以下行波的力波與質點速度同號均為正值，上行波的力波與質點速度為異號，由此沉樁系統的波動方程可以變形為：

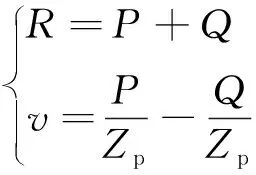
(19)

(20)

(21)

那么將下行力波帶入求解對應的微分方程，并考慮初始條件t=0,up=0即可得到樁的動態響應。

3 結論

(1) 通過對沉樁系統各部件間的相互作用進行了動力學分析，建立了錘、墊層和樁三者間的作用模型并運用拉氏變換推導出了沉樁過程中的錘擊力解析解，并運用其對實際工程中“重錘輕擊”的合理性進行了驗證。

(2) 分析了墊層剛度對沉樁過程中錘擊力的影響，結果表明墊層的剛度越大，產生的錘擊力峰值越高，錘擊力持續時間越短，指出可以通過選用合適的墊層對錘擊力進行調整以提高沉樁效率并且能夠避免沉樁過程中樁錘與樁的損壞。

(3) 基于波動理論，針對兩種土體介質模型，建立了沉樁系統理論分析模型。