雙駁半主動升沉補償及其在“世越”號打撈案例中仿真應用研究

張峰瑞，侯交義，李人志， 寧大勇，弓永軍

(大連海事大學 船舶與海洋工程學院，遼寧 大連 116000)

引言

隨著海上運輸業、工業等領域的充分發展，發生海上事故的風險也在不斷提高，受到海上風浪與海水深度的制約，通常情況下打撈一艘大型沉船極為困難，為此，考慮將升沉補償技術應用于大型船只的打撈中。

升沉補償技術最早在20世紀70年代被提出[1]，用于改善由海浪造成的母船運動對所提升負載的影響。升沉補償系統可分為被動式(Passive Heave Com-pensation，PHC)、主動式(Active Heave Compensation，AHC)和半主動式(Semi-Active Heave Compensation，SAHC)三種。PHC系統承載力強但是補償效率不高；AHC系統補償效果好，但承載能力弱，且需要較大的供能設備；而SAHC系統結合兩者優勢，兼具大承載力和高補償效率[2]。目前升沉補償技術已取得一定研究和應用，HUSTER等[3]使用PHC系統投放和回收ROV，補償效率68%；DO等[4]設計了一種基于干擾觀測的AHC非線性控制器；QUAN等[5]在實驗水池模擬深海ROV在不同深度下纜繩柔性對PHC和SAHC的拉力與位移影響；宋豫等[6]針對大噸位波浪補償系統的相應滯后問題，提出了船用起重機SAHC系統的多狀態反饋復合控制方法。然而，大噸位打撈工作通常需要多纜多船協同提升，升沉補償的應用還相對較少。2001年核潛艇“庫爾斯克”號打撈采用了26組液壓同步提升AHC系統，通過船體傾角控制液壓缸補償提升鋼纜的恒拉力[7]；2017年采用PHC方案完成打撈的韓國“世越”號沉船[8],侯交義、張增猛等[9-10]仿真研究了沉船提升PHC系統的補償特性，并設計了一種沉船同步提升升沉補償試驗平臺。目前SAHC技術還沒有應用實例，考慮其出色的補償效果與承載力大等優點，SAHC技術將會用于某些安全性和穩定性要求更高的大噸位打撈工作中。

本研究建立了SAHC液壓系統、柔性纜繩與沉船負載間的耦合系統數學模型，推導了各吊點補償量，并基于韓國“世越”號打撈案例，仿真模擬同等條件下SAHC系統的補償效果，研究了多組半主動升沉補償裝置協同懸吊沉船時，系統的負載特性和補償效果。

1 “世越”號打撈系統

韓國“世越”號客船沉沒于2014年，2017年由上海打撈局完成打撈工作。船長為145 m，寬為22 m，型深為14 m，事發地點水域深度約為44 m。綜合考慮沉船強度和水域狀況，實際采用PHC系統的雙駁抬吊實施打撈。事實證明，PHC系統有效緩沖了抬浮駁船運動導致的變動負載力，為“世越”號平穩提升發揮重要作用。

“世越”號采用雙駁抬吊打撈方法，如圖1所示，兩艘抬浮駁船與沉船通過66根起吊鋼絲繩連接(每側33根)。鋼絲繩下端連接事先鋪墊在沉船底部的33塊托底鋼梁，上端連接多股鋼絞線，鋼絞線與PHC提升裝置相連。“世越”號打撈的提升系統為66組帶有PHC的同步提升液壓缸。

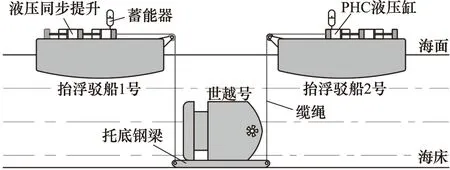
圖1 雙駁PHC打撈“世越”號示意圖

打撈開始時，先對各提升液壓缸同步加載至預設載荷，再對各吊點單獨加力直至沉船完全離開海床，此后保持載荷同步提升。打撈過程將沉船從44 m水深提升至出水13.5 m，實際離底重量8500 t，實際出水重量11500 t。為減輕“世越”號整體起吊重量，事先對其安裝內氣囊和外置浮筒，增加約3100 t的額外浮力[11]，實際打撈時3艘船舶的參數見表1。

表1 “世越”號沉船及雙駁船實際參數

本研究使用SAHC系統替換實際打撈中的PHC系統，參考3船實際尺寸、質量與水深，對沉船離底后水下懸掛階段進行建模與分析。

2 雙駁SAHC系統數學模型

2.1 SAHC液壓系統

本研究SAHC系統構成如圖2所示，分為主動補償器(AHC部分)、被動補償器(PHC部分)以及剛性連接件3部分。兩補償器采用非對稱液壓缸并聯承受負載力。AHC部分通過電液伺服閥驅動液壓缸運動實現位移補償，PHC部分的無桿腔連接蓄能器，蓄能器初始壓力為負載的平衡壓力。僅研究補償系統的負載特性，故本研究忽略負載提升部分。

圖2 半主動升沉補償系統

1) AHC部分

主動補償部分主要由伺服閥和雙作用液壓缸組成。以閥芯正向開啟為例，AHC缸伸出時，無桿腔進油，有桿腔回油，則液壓缸的負載壓力：

(1)

式中，FAHC—— AHC缸負載力

A1—— 無桿腔面積

p1,p2—— 分別為無桿腔和有桿腔的油液壓力

n—— 比例系數：

(2)

式中，A2—— 有桿腔面積

Q1,Q2—— 分別為AHC缸進油與回油流量，也是伺服閥兩閥口流量

(3)

式中，Cd—— 閥芯流量系數

w—— 伺服閥閥口面積梯度

uv—— 伺服閥口開度

ps—— 系統供油壓力

ρ—— 油液密度

聯立式(1)～式(3)，則AHC缸兩腔壓力可通過負載壓力與油源壓力表示為：

(4)

以上為閥芯正開情況，閥芯負開時的推導過程類似，此處不再推導。則根據油液流動的連續性方程，AHC缸的運動速度為：

(5)

其中：

式中,xAHC—— 液壓缸活塞桿位移

V—— AHC缸總油液體積

βe—— 油液的有效體積彈性模量

Ct，Ci—— 分別為由壓力引起的AHC缸內外泄漏系數

2) PHC部分

當PHC系統單獨使用時，其蓄能器類似非線性彈簧，緩沖負載力。而在SAHC系統中，蓄能器的主要作用是平衡靜止狀態下的負載力，減小AHC缸受載。在打撈工作進行前需要對蓄能器預加一定的初始壓力，該初始壓力應與纜繩上的負載相平衡，即：

(6)

式中，Gw—— 沉船的水下重量

Ax—— 與蓄能器相連PHC缸的補償腔面積

系統工作時，AHC缸進行位移補償，PHC缸桿被AHC缸帶動，離開平衡位置，蓄能器氣體的體積變化量為：

ΔV=AxxAHC

(7)

(8)

式中,V0為蓄能器中氣體初始體積。

聯立式(6)～式(8)，可得工作狀態下PHC缸承載力隨AHC缸補償量變化公式：

(9)

3) SAHC系統負載力

由SAHC系統示意圖4所示，剛性連接塊承受來自纜繩、AHC和PHC 3部分的合力作用，由于PHC缸抵消大部分纜繩負載力，可得AHC系統的主要負載力為：

FAHC=FL=Ft-FPHC

(10)

式中,Ft為纜繩拉力。

聯立式(5)、式(9)、式(10)，可得SAHC位移補償量與閥芯開度、纜繩負載力間的微分方程：

(11)

2.2 負載運動

由于水下沉船受不均勻拉力作用，會產生6個運動自由度，為簡化模型，只考慮幅度較大的升沉、橫搖和縱搖3個運動自由度，如圖3所示。

圖3 沉船水下受力與運動姿態

1) 沉船升沉動力學建模

當僅考慮沉船的升沉運動，沉船受到66根纜繩豎直向上的拉力、自身重力、海水浮力和升沉水阻力的合力作用，如圖4所示。根據牛頓第二定律，沉船重心的升沉方向加速度為：

缺點：①由于計算量很大，ACC控制盤核心CPU要求較高，必須選擇大型PLC（如三菱Q系列、西門子S7-400系列等）。②PLC作為一個控制裝置，在邏輯控制方面較有優勢，但是在數據運算中功能沒有DCS強大；運算部分的個別功能，需要設計專門的邏輯功能塊來實現［4］。③人機界面增多，在中央控制室高度集中的情況下不便布置，不夠簡潔，影響集控室的美觀度。

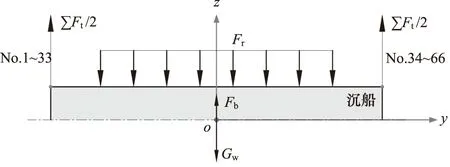
圖4 沉船升沉運動受力

(12)

式中，hw—— 沉船重心升沉位移

Fti—— 各吊點所受拉力(i=1,2,…,66)

fb—— 沉船受海水浮力

fr—— 沉船受海水繞流阻力

mw—— 沉船質量

g—— 重力加速度，取9.8 m/s2

沉船升沉運動時受海水的繞流阻力：

(13)

式中，CD—— 繞流阻力系數，取2

ρ—— 海水密度，取1025 kg/m3

S—— 船的迎流面積，近似取沉船水平截面積

2) 沉船橫搖、縱搖旋轉動力學建模

使用歐拉角法描述沉船的空間轉動，旋轉次序為先橫搖后縱搖。定義沉船第i個吊點位置，以沉船重心為原點的坐標表示為：

P0i=[x0iy0iz0i]T

(14)

則沉船發生空間轉動后，任意吊點的新坐標為：

Pi=Ty(θy)Tx(θx)P0i

(15)

式中，P，P0—— 分別為任意空間點經旋轉變換的新舊坐標

Tx，Ty—— 分別為橫搖和縱搖的變換矩陣

其表示為：

(16)

(17)

式中，θx，θy分別為橫搖角與縱搖角，(°)。

由于所有纜繩足夠長，假設各纜繩始終沿豎直方向拉動沉船，忽略纜繩的偏轉。則沉船上的任意吊點的拉力將會在沉船重心產生空間力矩：

(18)

式中，OPi—— 拉力作用點對沉船重心的矢徑

Fi—— 該點的拉力矢量

xi,yi,zi—— 分別為吊點到沉船重心的距離分量

根據叉乘準則，第i點拉力對沉船重心的橫搖與縱搖分力矩Mxi和Myi分別為：

(19)

則沉船受全部纜繩合力產生的橫搖與縱搖轉動角加速度分別為：

(20)

式中，Mrx,Mry—— 沉船橫、縱搖轉動水阻力矩

Jx,Jy—— 分別為沉船橫搖和縱搖轉動慣量

沉船轉動時所受水阻力矩，可通過對各回轉半徑處所受水阻力(式(13))積分獲得。簡化沉船為一長方體，如圖5所示，水阻力在沉船上下和左右迎流半表面成對產生，以沉船上下迎流面為例，可推導水阻力矩公式為：

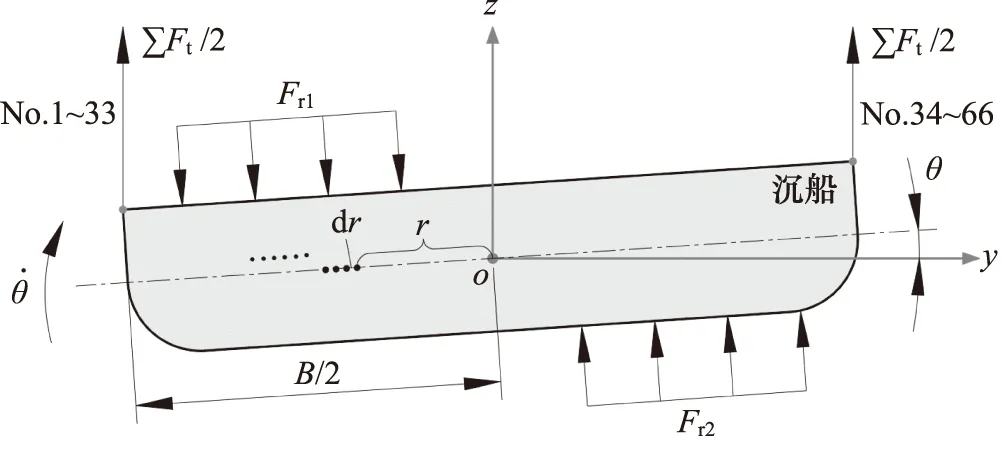
圖5 沉船回轉運動所受水阻力矩

(21)

式中，L,B分別為迎流表面的長度和寬度。

2.3 纜繩模型

鋼絲繩具有一定的柔性，可等效為具有一定彈性剛度的線性彈簧，其伸長量與所受拉力的關系為：

(22)

式中,Cr—— 鋼絲繩的等效剛度

Δl—— 鋼絲繩伸長量

Cg—— 鋼絲繩填充系數

A—— 纜繩橫截面積

E—— 鋼絲彈性模量

lr—— 纜繩原長

沉船懸吊時，單根纜繩的伸長量為：

Δl=xd-xSAHC-Δxw+l0

(23)

式中，xd—— 該纜繩上SAHC的理論補償量

Δxw—— 該纜繩對應的沉船吊點豎直方向的位移變化量

l0—— 纜繩受沉船重力的初始伸長量

沉船吊點的豎直位移變化量與沉船自身的升沉、橫搖和縱搖運動相關，即：

Δxwi=hw+zi-z0i

(24)

式中，zi為沉船發生橫、縱搖轉動后，吊點的豎直坐標，該坐標通過式(15)變換得到。

2.4 SAHC補償量計算

實際海面上，船舶在海浪作用下也會產生6個自由度的運動，其中的升沉與橫縱搖運動對水下負載的影響最顯著。SAHC系統的理論位移補償就是該補償點與初始位置的偏差量，并以此作為AHC系統的輸入量，再由主動執行器進行位置跟蹤。

與沉船吊點位移計算類似，某時刻駁船吊點的位置偏差，即SAHC的理論補償量，也與駁船3個主要運動相關：

xdi=hb+zdi-zd0i

式中，hb為駁船重心的升沉位移；zdi為由駁船轉動造成的第i個吊點的豎直坐標，已知駁船橫縱搖傾角即可由式(15)求得。

3 雙駁SAHC系統仿真

仿真基于MATLAB/Simulink，參照“世越”號的實際打撈案例，按照駁船1號、“世越”號沉船和駁船2號的次序排列。兩艘駁船間距為14 m(“世越”號型深)，單艘駁船上的相鄰吊點間距4 m。假設沉船已經完成離底，并懸吊于40 m水深(總水深44 m)，雙駁船受海浪激勵運動，補償系統工作。

因缺少實際打撈時沉船的運動數據與纜繩拉力數據，仿真將分別以PHC和SAHC兩種補償方式進行，對比分析兩種補償器的補償效果。

3.1 雙駁水動力仿真

雙駁系統仿真以駁船的升沉、橫縱搖運動作為輸入量，因此為了得到與實際海況下相近的駁船運動時域數據，采用水動力仿真獲得兩艘駁船在真實海況參數下的運動時域數據，實際海況參數如表2所示[12]。

表2 “世越”號離底后的海況參數

水動力仿真得到的兩艘駁船的升沉運動、橫縱搖傾角的300 s時域結果如圖6所示。由于海浪主要從駁船的右側涌來，可見兩艘駁船的橫搖運動較為強烈，而縱搖運動較小。

圖6 雙駁船水動力仿真時域數據

3.2 雙駁SAHC與PHC系統仿真

駁船上的66組SAHC系統相互獨立工作，各吊點位移補償量由2.4節公式計算，并通過PID控制器進行位置追蹤。無論是仿真中或是實際，位移補償都會存在補償誤差，因此無法徹底消除負載位移和纜繩張力的變動。仿真過程將忽略油液的壓縮性和泄漏作用，不考慮沉船受水流擾動的影響。液壓系統參數如表3所示，纜繩參數如表4所示。

表3 SAHC液壓系統仿真參數

表4 鋼絲纜繩參數

采用SAHC和PHC補償器的沉船重心升沉運動仿真結果如圖7所示。在180～210 s時，兩艘駁船的升沉和橫搖幅度有較大峰值，并且在沉船升沉運動中也有體現：只使用PHC系統的沉船重心升沉幅度最大約為0.2 m；而SAHC系統的幅度最大約為0.02 m，較PHC幅值下降約90%。

圖7 SAHC與PHC沉船重心的升沉位移仿真結果

沉船橫、縱搖的仿真結果如圖8所示，相較駁船最大0.6°的橫搖角度，SAHC系統使沉船橫、縱搖運動基本平穩，最大橫搖角度約3×10-4(°)，最大縱搖角度約2×10-7(°)；而采用PHC的沉船橫、縱搖在整體上發生了偏轉，推測是受雙駁船不均勻拉力的作用，且沉船重心高于受力面，在無外力的矯正下會發生持續偏轉。可見SAHC系統擁有更強的負載穩定性。

圖8 SAHC與PHC沉船橫縱搖仿真結果(左軸對應SAHC，右軸對應PHC)

“世越”號的水下重量約為5400 t(含外加浮力)，分配到每根纜繩上的拉力約為801 kN。由于每艘駁船上的33根纜繩間的拉力差別較小，因此只提取每艘駁船上的首個吊點，即1號和34號纜繩進行對比，使用SAHC與PHC下的纜繩拉力F結果如圖9所示。在約180 s時，2根纜繩拉力均到達峰值，使用PHC的2根纜繩拉力峰值約為840 kN；而使用SAHC的拉力峰值約為803 kN，較PHC拉力減少約95%。

圖9 SAHC與PHC纜繩張力仿真結果

4 結論

本研究基于“世越”號打撈案例，建立了雙駁船66組SAHC沉船打撈系統的數學模型，包括負載動力學模型、SAHC液壓系統及柔性纜繩模型，通過水動力仿真獲得雙駁船的運動時域數據，并通過MATLAB/Simulink平臺進行仿真。對比研究了SAHC與PHC兩種補償器的補償效果，分析沉船的升沉位移、橫縱搖傾角和纜繩拉力等負載特性，結果表明：

(1) 相比PHC系統，采用SAHC的雙駁打撈系統更能有效降低沉船的升沉位移，最大位移幅值下降約90%；

(2) SAHC雙駁打撈系統對沉船回轉運動有更強的抑制作用，而PHC系統的沉船回轉運動出現失穩現象；

(3) SAHC系統可有效削弱單根纜繩上的拉力變化，最大拉力相比PHC系統減少96%。

所研究的雙駁多纜打撈仿真中，僅考慮了較理想的條件，因此在之后的研究中，需要引入更多現實因素的影響。同時需要進行實驗，進一步驗證仿真結果的正確性。