一種改進的快速求射線與三角形交點的算法

張煒喆

（同濟大學電子與信息工程學院，上海，201804）

0 引言

隨著圖形學技術的突破和發展，光線追蹤算法正在逐步取代光柵化算法，成為實時渲染領域新的主流技術。不論是光線追蹤還是光柵化，它們都離不開三角形這一最基礎的幾何模型。因此，能否快速準確的計算出光線和三角形的交點決定了整個渲染過程的效率。

解決該問題的一個十分樸素的思路是首先聯立射線的參數方程和平面的參數方程，求解出光線與三角形所在平面的交點，然后通過三次叉積的計算來判斷該交點是否在三角形內部。但是由于要經過兩個復雜的步驟以及多次向量計算，該算法在如今并沒有被實際項目采用。M?ller和Trumbore后來提出了一種改進的被簡稱為MT的算法[1]，也是現在最為通行的算法，它將三角形和射線的交點用三角形的重心坐標的形式表示，經過一系列移項，使其轉化為形如Ax=c的形式，其中A是一個可逆矩陣，x和c都是列向量。在此基礎上，MT算法利用克萊姆法則對該等式求解，從而可以得到三角形與射線交點的用重心坐標表示的數學形式。該算法極大地降低了計算射線-三角形交點的時間復雜度。

目前存在的更快的求解射線與三角形交點的方法大多從利用各式各樣的數據結構來優化的角度出發，比如基于空間劃分，將圖像空間遞歸的拆分為不同層次的樹結構[2]，或是通過層次包圍，動態的計算包圍了三角邊頂點的最小矩形包圍盒[3]等。這些算法在提高計算效率的同時也大幅增加了內存空間的開銷。

本文從純算法理論的角度出發，旨在減少單位時間內基本運算的次數。首先通過一次坐標變換，將射線和三角形從全局坐標系轉換到重心坐標系中，再求解變化后的坐標的交點。該算法所用到的計算步驟比MT算法更少，因此可以做到每次求解三角形與射線交點的速度都比MT算法更快。此外，該算法構造變換的方式能夠確保其矩陣形式所使用的許多系數為此前被預計算出來的值，不需要做多余和額外的存儲，因此能夠使得預處理的內存開銷最小化。

相較于其他算法，該算法具有良好的拓展性和應用價值。對于已經使用了MT算法實現的光線追蹤器或是光柵化渲染項目，不需要大幅調整自身的代碼結構，而只需要將其中用MT算法求解光線與三角形交點的模塊替換為本文提供的算法就可以在得到相同圖像的同時大幅提高圖片渲染以及圖像生成的效率。對于使用數據結構來加速計算光線與三角形交點的案例，該算法的思路依然可以部分應用于其中，從而加速整個計算的過程。

1 數學定義

2 算法步驟

在三角形初始化的過程中，首先計算出定義1.3中提到的從全局坐標系到重心坐標系的轉換矩陣T，并將該矩陣作為三角形信息的一部分儲存下來。由于矩陣計算的過程會把該坐標轉換為齊次坐標系中進行計算，根據齊次坐標系的性質，易知該矩陣第四行的值不參與相關涉及到變量的運算，且它的值一定為( )0,0,0,1，故可以只儲存該矩陣前三行的內容，從而節省了大量的內存空間。

當我們計算出了轉換矩陣T的值，則可以按照以下四個步驟得到坐標的重心表示形式：

3 時間復雜度分析

根據MT算法的描述[1]，它至少需要進行三次向量混合積的計算，而每次向量混合積的計算需要12次乘法運算和5次加法運算（此處暫時不考慮向量中有0的情況）。為了方便統計和比較效率，我們定義1次乘法運算或1次加法運算為1次元運算。忽略MT算法中涉及到的標量除法等耗時較少的計算，則MT算法至少需要進行34次元運算。

對于本文提出的方法，按照算法步驟中的4個步驟依次統計運算次數：

(a)該步驟是一個4×4的矩陣左乘一個4× 1的列向量，由于該矩陣的第四行為(0 ,0,0,1)，列向量的第四行為1（齊次坐標的性質），展開化簡后可以得出需要的元計算為18次。

(b)該步驟為一個標量除以一個標量，由于除法可以看作是乘法的逆運算，故需要元計算1次。

(c)該步驟需要2次標量乘法和2次加法，合計元計算2次。

(d)該步驟為比較的過程，不計入運算的步驟中。

將以上四個步驟需要的元計算次數進行加總，得出本文提出的算法需要的元計算次數至少為23次，遠小于MT算法需要的34次。

4 空間復雜度分析

由于MT算法不需要儲存額外的變量信息，因此不存在超出所有變量自身以外的內存空間開銷。

本文提出的算法所需的額外內存占用主要在于預處理時使用的轉換矩陣T。由于不需要考慮T矩陣第四行的值，所以單個三角形需要額外儲存的內存為12個自由變量。同時，由于該矩陣只與三角形自身的性質相關，而與射線的參數無關，因此該部分內存可以在計算完所有需要和同一三角形相交的射線后釋放，總體上來說不會大幅增加內存的消耗。

5 實際運行結果

本文采取了兩種方式來比較該算法和通用的MT算法的性能：一是分別獨立實現兩種算法，用不同三角形數量的測試集各自進行一輪測試；二是將該算法分別嵌入一個完整的光柵化項目和一個完整的光線追蹤器中，比較在實際項目中該算法和MT算法的效率。

實驗表明，在這兩種情況下，本文提出的算法都比MT算法更快。

■5.1 獨立計時實驗

此部分比較了本文提出算法的運行時間和原始版本的MT算法的運行時間，同時也比較了MT算法在sse4框架[4]下的一個改編版本：該框架經過高度的調整，可以在現代CPU上快速的執行MT算法。根據文獻[5]設計的測試程序，該程序能夠生成指定數量以及指定射線-三角形命中率（射線-三角形命中率指的是有射線能夠與之相交的三角形占總三角形個數的比例）的射線和三角形的集合，其中每條射線都與至少一個三角形相交。該程序能夠進行本文提出算法的12-自由元版本、9-自由元版本、原始的MT算法以及在sse4框架下的改編MT算法的比較。

在未經特殊申明的情況下，本文涉及的所有實驗皆在以下運行環境運行：CPU 2.8GHz Core i7-7700HQ，內存16 GB of RAM，硬盤512 GB of SSD，操作系統Windows 10 2004 64位，IDE編譯優化設置為-O3級別的Visual Studio 2019。

本文對上述涉及到的兩種算法進行了輕微的修改，但是仍然盡可能地使其接近原始算法的意圖，以方便能用C++的形式進行復現。由于當前sse4框架下的MT算法還使用了SIMD功能以提升其并行性，本文在實現該算法時刪除了這一特性以保障一個平等的實驗測試環境。值得一提的是，SIMD提供的并行特性并不與本文提出的算法排斥，因此將該部分功能添加到本文提出的算法中將是未來的研究方向之一。

表1展現了本次實驗的結果。表格中展現的百分數代表該算法在當前實驗環境下運行所需的時間和MT算法在當前實驗環境下運行所需時間的比例。可以看到，不論三角形數和射線-三角形命中率如何變化，本文提出算法的12-自由元版本都穩定的快于9-自由元的版本，而12-自由元的版本在所有實驗條件下運行時間均在MT算法的30%～50%之間。當射線-三角形命中率僅為0.1時，12-自由元版本依然在運行效率上略高于sse4框架下的MT算法，隨著射線-三角形命中率的增高，12-自由元的版本和sse4框架下的MT算法的效率差距逐漸拉大，在射線-三角形命中率高達0.9時，12-自由元的版本運行時間約為sse4框架下的MT算法的50%左右。當射線-三角形命中率為最低的0.1時，9-自由元的版本比sse4框架下的MT算法效率略低，但是隨著射線-三角形命中率增大到0.5和0.9，其運行速度反超sse4框架下的MT算法，處在12-自由元的版本和sse4框架下的MT算法中間。

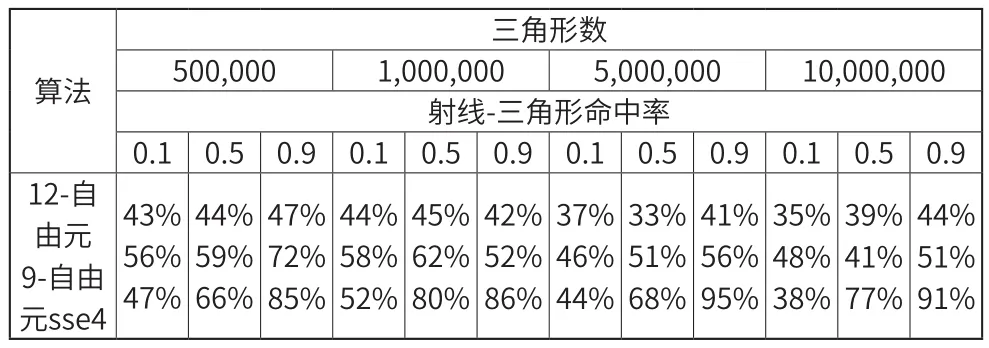
表1 不同數據集下三種算法和MT算法運行效率對比

值得注意的是，對于每個三角形，sse4框架下的MT算法需要預先計算一個頂點、兩條邊和三角形的法線，總共需要48個字節的額外內存開銷（假設所有數據為單精度浮點數），而9-自由元的版本僅需額外36個字節的內存空間（假設所有數據為單精度浮點數）。

■5.2 在真實場景下的應用

為了測試本文提出的算法在真實復雜場景下的正確性和有效性，該部分選取了兩個顯示效果明顯的渲染項目，其中一個項目由Blinn-Phong光照模型[6]在光柵化下實現，另一個項目則使用了一個初階版本的路徑追蹤器完成。

本次測試所做的工作僅僅為將這兩個項目中用MT算法求解射線-三角形交點的函數修改為本文提出的算法，其余部分未做任何改動。最終得到的結果如表2所示。可以看到，在真實場景下本文提出的算法在效率上的提升不如上一個實驗顯著。原因在于在真實的渲染項目中，除了計算射線-三角形的交點以外，還有其他的函數消耗大量時間，比如模型的加載，計算光的反射，圖層的處理等。這兩個場景最終渲染生成的圖像如圖1和圖2所示。

表2 兩個場景下本文提出的算法和MT算法運行效率對比

圖1 基于Blinn—Phong光照模型和光柵化渲染

圖2 基于路徑追蹤器渲染

6 結論

本文提出并測試了一種新型的計算射線-三角形交點的方法，它以對每個三角形進行預處理和儲存少量的額外信息為代價，能夠快速的求解出射線與三角形的交點。儲存的額外信息并不會妨礙渲染工作的進行，即使是在一些大型的渲染項目中，它依然可以穩定并準確的運行。

該算法在效率上遠遠優于通用的MT算法，并在一定條件下優于MT算法的改進版本。在完整的渲染工程中，本文提出的方法在獲得相同視覺效果的同時取得了比MT算法更快的結果。進一步的工作可以考慮將本文提出的算法和前述所涉及到的數據結構相結合，以期能夠得到時間復雜度更小的綜合實現方案。

文獻[5]指出，世界上并不存在一種最快的求解射線與三角形交點的方法，不同的算法在不同的運行條件和數據集下各有優劣。隨著圖形學和實時渲染技術的進一步發展，對于在短時間獲取穩定準確圖像的需求不會減少。本文提出的算法正是在這樣的背景下進行的一點思考，如果能夠該思路融入到一些已經實現的光柵化項目和路徑追蹤器項目中，將很有希望能夠獲取更大的成果。