深度學習網絡的微電網變壓器電壓波動抑制研究

郭永鑫，肖洪光，楊 璐

(國網吉林省電力有限公司，吉林 長春 130062)

0 引言

微電網作為充分發揮分布式能源效用的主要形式，能夠滿足當前能源需求的快速提升。其中，以變壓器為核心的微電網結構成為當前研究領域的關注熱點[1]。微電網變壓器受干擾后易產生電壓波動問題，嚴重影響微電網供電質量，直接或間接導致的經濟損失越來越嚴重[2]。抑制變壓器電壓波動需以準確的電壓波動估計為基礎[3]。

作為機器學習的主要組成結構，深度學習網絡通過學習樣本內在規律完成信息識別[4]。深度學習網絡中的置信網絡具有特征提取與分類功能[5]，可應用于變壓器電壓波動估計。為此，提出了基于深度學習網絡的微電網變壓器電壓波動估計與抑制方法，采用深度學習網絡完成特征提取功能，以自動生成特征替代人工設置特征，準確估計電壓波動情況；在電壓出現波動條件下，通過組合抑制方法抑制其波動，保障微電網的穩定運行。

1 微電網變壓器電壓波動抑制方法

1.1 微電網系統結構

微電網系統結構包括主電網、變壓器、光伏陣列、風機、蓄能系統等[6]。變壓器包含三個層級[7]，分別是H橋型交流電源(alternating current，AC)與直流電源(direct current，DC)變流器級聯構建的輸入級、雙向全橋DC-DC變換器變流器并聯構建的隔離級、完成電壓源型逆變的輸出級。三個層級分別具有連接主電網不同電壓等級、變換電壓、提供低壓交流接口引出微電網交流母線的功能。微電網交流母線利用DC-AC、AC-DC-AC變換器連接風機與光伏等分布式能源。具有輔助本地供電功能的蓄能系統利用DC-AC變換器與微電網連接。微電網系統結構框架如圖1所示。

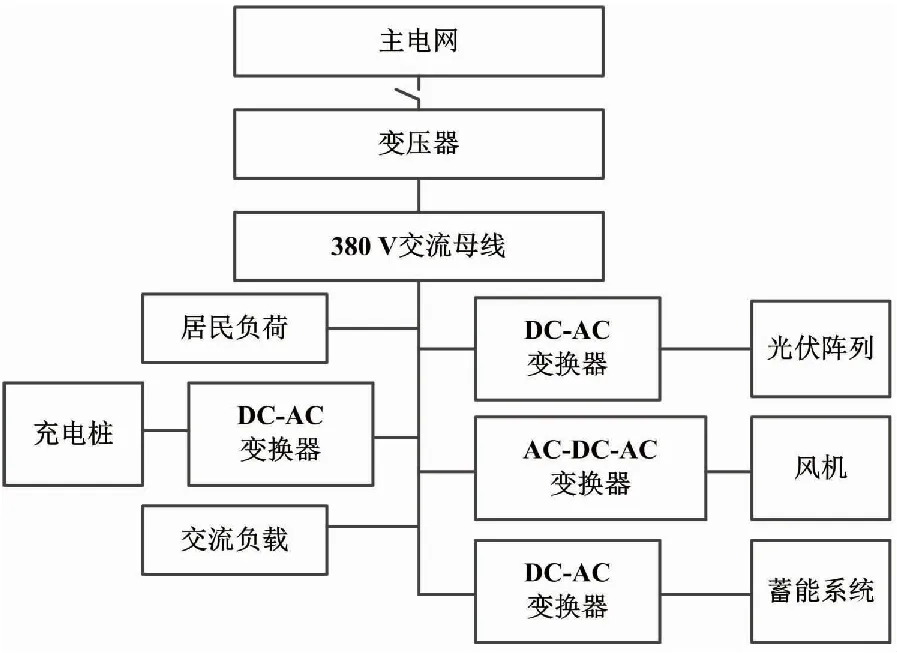
圖1 微電網系統結構框架

變壓器受干擾后易產生電壓波動問題。引起微電網變壓器電壓波動的主要因素如表1所示。基于微電網變壓器電壓波動主要因素造成的電壓波動波形，采用深度學習網絡中的置信網絡構建模型，提取波形特征，根據特征估計電壓電壓波動情況。

表1 微電網變壓器電壓波動的主要因素

1.2 變壓器電壓波動估計

1.2.1 深度學習網絡結構

作為具有多隱含層的神經網絡，深度學習網絡中反向傳播(back propagation，BP)神經網絡和受限玻爾茲曼機(restricted boltzmann machine，RBM)的數量分別為一層和多層。通過逐層貪婪學習算法調整不同層級之間的連接權重。無監督學習性能極強，能夠最大限度地防止類別劃分性能較差以及過度擬合缺陷的出現[8]。圖2所示為深度學習網絡結構。

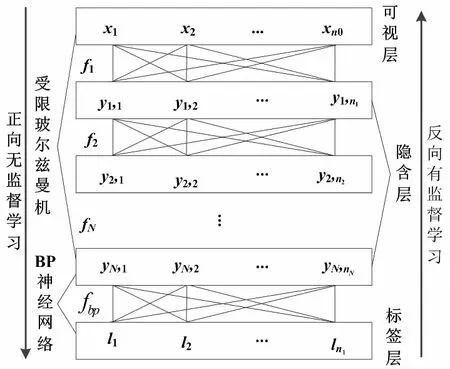
圖2 深度學習網絡結構圖

圖2中：x1、x2、xn0、f1、f2、fN和l1、l2、lnl分別為可見層輸入情況、相鄰單元層間連接權重向量和標簽層不同單元情況；yx,z和ftp分別為第x個隱含層第z個單元情況和BP神經網絡權重向量。

作為基于能量函數的概率建模方法，受限玻爾茲曼機由可視層和隱含層共同組成[9]。其主要功能為利用棧式逐層堆疊學習初始數據內復雜化準則。深度學習網絡訓練由三個環節組成，分別是模型初始化環節、正向無監督學習環節和反向有監督學習環節。

1.2.2 深度學習網絡計算原理

設(v,y)為給定狀態，通過式(1)能夠描述深度學習網絡可見層和隱含層單元的統一設定能量函數：

(1)

式中：λ=(f,ε,φ)為深度學習網絡參數；fij為第i個可見層單元與第j個隱含層單元之間的權重，只有鄰近兩個層間具有連權重接；εi為第i個可見層單元；φj為第j個隱含層單元的偏置；vi、yi均為狀態參數；n為可見層單元數量；m為隱含層單元數量。

深度學習網絡狀態概率具有正則分布特性[10]，因此可利用式(2)描述隨機狀態的統一概率分布：

(2)

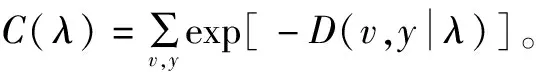
(3)

(4)

式中：s為訓練樣數量。

利用深度學習網絡對數似然函數L(λ)最大化處理，獲取深度學習網絡參數λ，同時擬合訓練樣本。此時，可視層輸入數據的特征為隱藏層：

(5)

將比散度算法應用于對數似然函數中[11]，求解λ。以λ內包含的fij為例：

(6)

式中：Dvi,yj,1為訓練樣本參數；Dvi,yj,2為深度學習網絡定義的期望參數。兩者均可通過吉布斯采樣獲取。

在此基礎上，可優化fij，得到：

fij=βfij+α(Dvi,yj,1-Dvi,yj,2)

(7)

式中：β為動量參數；α為學習率參數。

εi與φj同樣可采用上述過程實施優化。

1.2.3 基于深度學習網絡的電壓波動估計

深度學習網絡中，不同隱含層特征向量維度與其單元數量相同。隱含層數量越多，模型提取的特征精度越高，電壓波動情況估計越準確。

電壓波動估計的實現流程是通過采集微電網變壓器電壓波動波形時域數據，經過數據預處理后建立批量輸入深度置信網絡模型。結合RBM正向無監督學習數據各層的特征，采用逐層貪婪算法修正各層單元的偏置值和隱層權重，并對順序輸入的不同電壓波動波形進行準確分類和標志。利用BP神經網絡對訓練樣本進行反向微調，完成模型訓練。根據輸入電網的數據，可以準確地提取出微電網變壓器的電壓波動特征。

1.3 電壓波動抑制

采用深度學習網絡提取電壓波動波形特征完成電壓波動估計。若電壓出現波動，則需對其進行抑制，保障微電網穩定運行。在采用比例諧振控制器作為抑制變壓器電壓波動的基礎上[12]，考慮到變壓器的可用補償容量，可得比例諧振控制器控制下變壓器輸出電壓為：

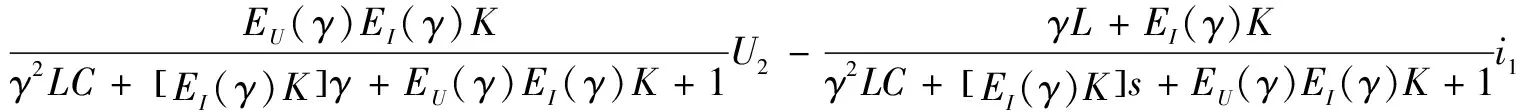
(8)

式中：EU(γ)為電壓控制器傳遞函數；EI(γ)為電流內環比例增益函數；K為調制增益參數；U2為輸出級參考電壓參數；i1為輸出電流參數。

根據式(8)可知，利用電壓控制器抑制電壓波動過程中，輸出電流i1正向增益EIR(γ)的變化將導致變壓器等效阻抗發生變化。

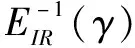
(9)

U1(γ)=EU(γ)U2-x(γ)i2-(1-O)x(γ)i2

(10)

式中：O為補償系數參數；i2為諧波分量參數；輸出層基波等效輸出阻抗參數。

O值能夠實時抑制變壓器電壓波動，其取值范圍在0～1之間。其值為0和1時，分別為變壓器當前為未補償和全補償狀態。O值與諧波阻抗呈反比關系。O值的提升可使電壓器電壓波動得到抑制，其值可根據變壓器可補償容量和實際諧波輸出容量得到。

2 實例驗證

以某微電網為研究對象，在監測系統中采集1 000組電壓數據。以800組實測變壓器電壓波動數據作為訓練樣本，微電網功率缺額和變壓器投切數據分別為180組和170組，短路故障數據為450組(單相接地、兩相短路和三項短路分別為150組)。剩余200組作為測試樣本，不同類別數據數量一致。

2.1 微電網變壓器電壓波動估計測試

采用本文方法進行研究對象變壓器電壓波動估計，構建深度學習網絡。模型輸入層單元數量同變壓器電壓波動監測節點數量一致。隱含層共6層，各層內均包含8個單元，第六層隱含層單元數量與提取特征數量一致。輸出層單元數量同電壓波動數據類型一致。由此確定，試驗過程中本文方法所用深度學習網絡共包含8層，總節點數量為1個輸入層×180+6個隱含層×8+1個輸出層×5=233個。設定模型參數：受限玻爾茲曼機迭代次數上限、學習率、動量參數分別為60、0.2和1。在深度學習網絡內輸入預處理后的訓練樣本數據。由于模型第六層隱含層單元數量為8，因此模型提取特征數量為8個。特征提取結果如表2所示。由表2可知，相同類型特征數據一致度高，而不同類型間特征數據差異顯著。這說明本文方法能夠有效提取電壓波形特征，且特征顯性突出，有利于提升電壓波動估計精度。

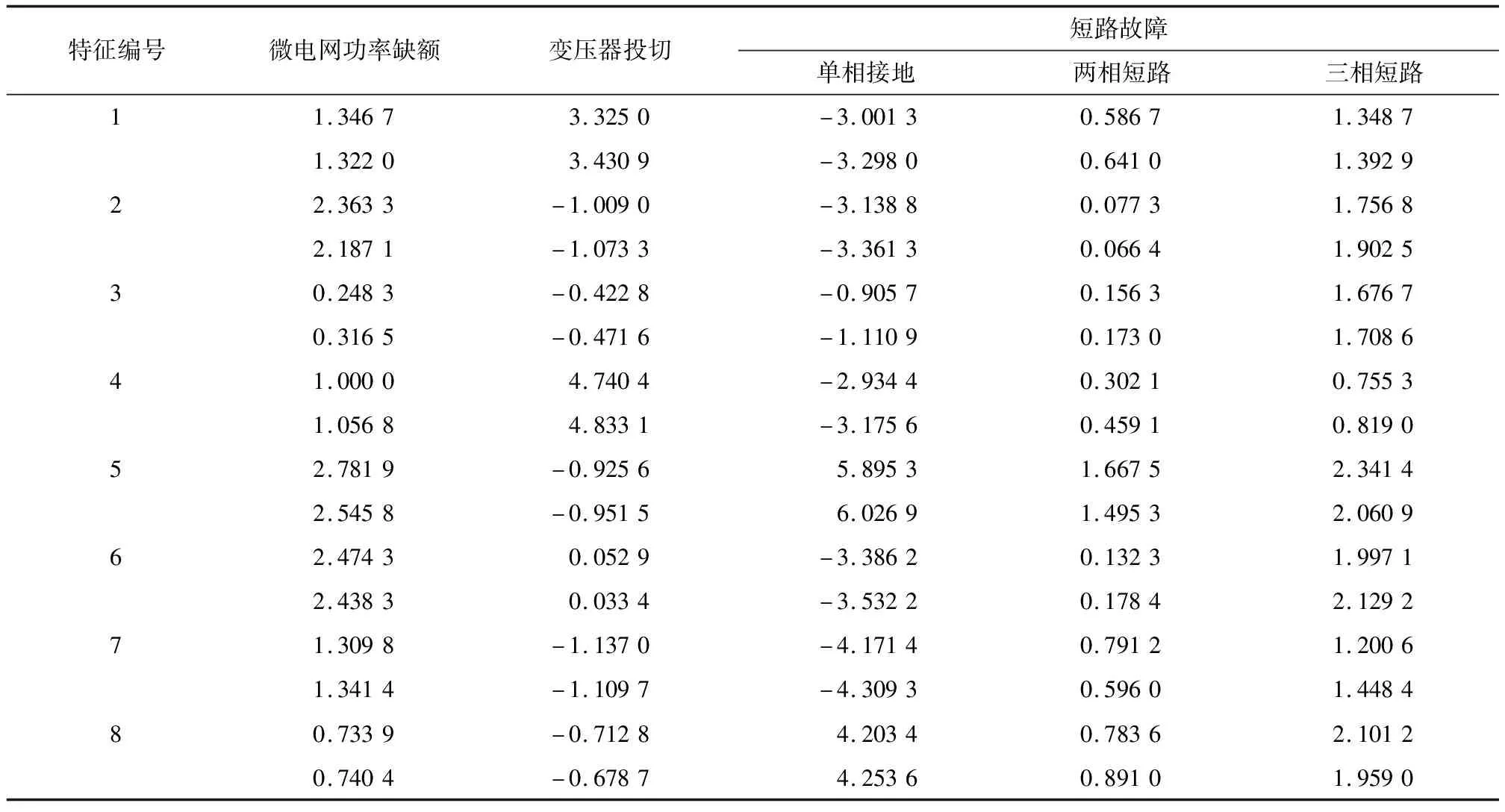
表2 特征提取結果

根據提取的特征對測試樣本進行估計，結果如表3所示。由表3可知，本文方法估計精度達到98.5%，充分說明本文方法能夠準確進行電壓波動估計。

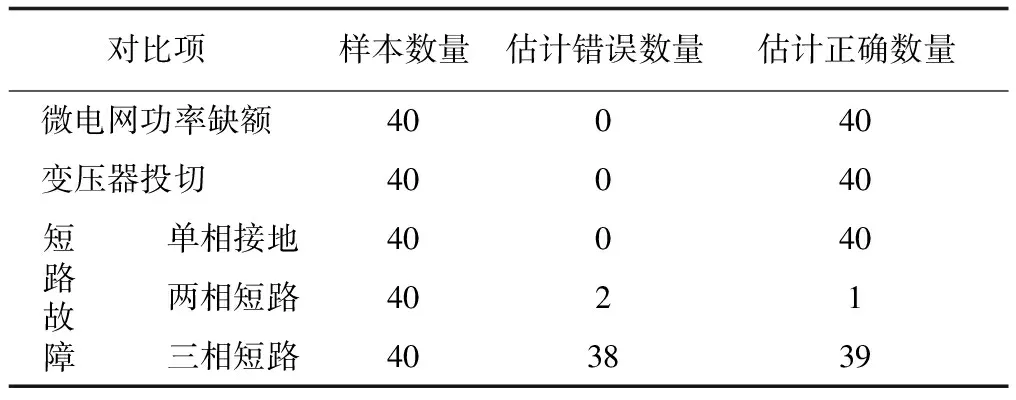
表3 測試樣本估計結果

2.2 微電網變壓器電壓波動抑制測試

在估計正確的測試樣本中隨機選取一組樣本，采用本文方法進行波動抑制。設定補償系數值為0.8，壓波動抑制結果如圖3所示。

分析圖3(a)可知，初始電壓波形中由于電壓波動導致波形畸變顯著，電壓波形整體畸變率達到18.8%。

分析圖3(b)可知，采用本文方法抑制電壓波動后，電壓波形與初始電壓波形相比更為平滑整體，波形畸變率降至2.9%，下降幅度為15.9%。由此說明本文方法能夠顯著抑制電壓波動，保障微電網穩定運行。

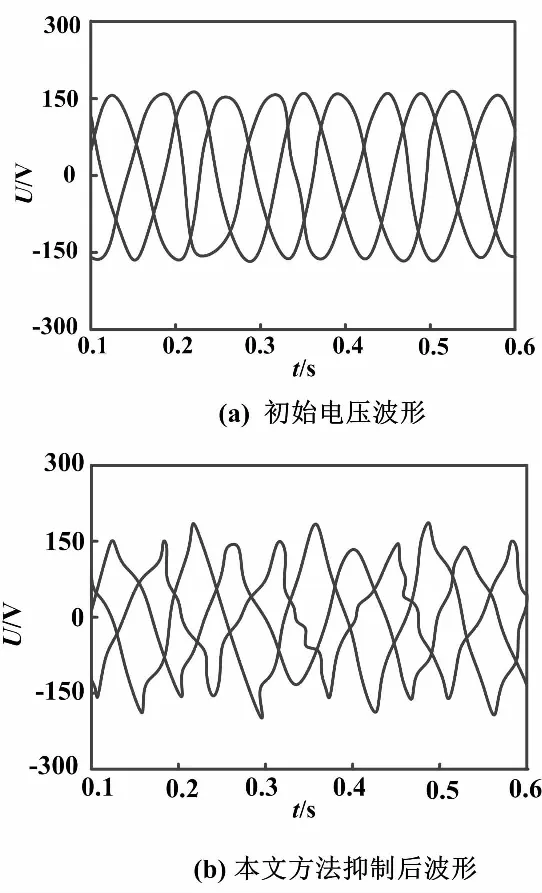
圖3 電壓波動抑制結果

2.3 補償系數設定分析

本文方法在不同補償系數設定值條件下，初始電壓波形畸變率下降幅度和電壓波動抑制過程中的能耗，補償系數設定如表4所示。由表4可知，隨著補償系數由0.2上升至0.9，畸變率下降幅度和能耗均隨之表現出明顯的上升趨勢。當補償系數為0.8時，畸變率下降幅度達到15.9%，能耗為4.76 J；當補償系數升至0.9時，畸變率下降幅度雖然上升0.7%，但能耗卻提升2.68 J，畸變率下降幅度與能耗提升不匹配。因此，補償系數確定為0.8。

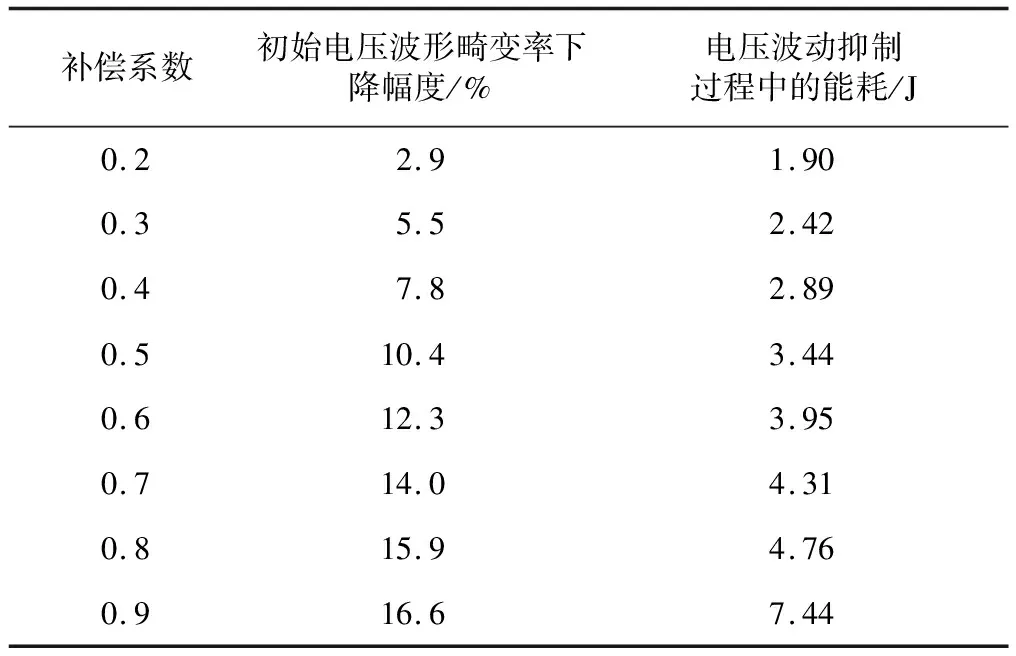
表4 補償系數設定

3 結論

本文研究深度學習網絡的微電網變壓器電壓波動估計與抑制方法，利用深度學習網絡中的置信網絡提取電壓波動特征估計電壓波動情況，并提出一種組合抑制方法抑制電壓波動。試驗結果顯示，本文方法能夠準確估計電壓波動情況，并顯著改善電壓波形畸變率，具有較高應用價值。