人工蜂群算法在螺絲內紋偏轉角度計算中的應用

姜金華，王 倩，姜景科

(1.上海第二工業大學智能制造與控制工程學院，上海 201209；2.上海大學機電工程與自動化學院，上海 200444)

0 引言

近年來，智能制造以飛躍式的跨度在制造業的各個維度得到了體現。螺絲作為零部件中重要的連接器件，在各類設備中都有廣泛的應用。而在拆解設備的過程，如果不能有效地對螺絲進行拆解，則會造成設備的暴力拆解。這將大大降低拆解的效率與廢舊材料的回收利用率。

機器視覺在當前的工業應用非常廣泛，包括視覺測量、產品分揀、視覺定位等[1-4]。本文中，機器視覺主要應用到拆解流水線的螺絲拆解中，主要用于獲取目標測量物的特征點，并對其進行相應的處理轉換，從而獲得所需的物理量[5-6]。

人工蜂群(artificial colony algorithm，ABC)算法是一種元啟發式群體智能優化算法[7]，由土耳其學者 Karaboga 在2005年提出。該算法是一種模擬蜜蜂群體尋找優良蜜源的仿生類智能計算方法[8-9]。人工蜂群算法的主要特點是不需要了解問題的特殊信息，只需要對問題的尋優結果進行優劣的比較[10-11]。通過蜂群個體在局部的尋優行為，最終在群體中使全局最優值凸顯出來，使得整個算法具有較好的全局搜索能力。這是一種廣義的鄰域搜索算法，有著較快的收斂速度，具有較強的通用性，能夠很好地與實際問題相結合，應用方向較為廣泛[12]。

1 系統結構設計

基于圖像處理的螺絲內紋偏轉角度測量的程序設計結構流程如圖1所示。

圖1 程序設計結構流程圖

首先，需要對原始圖像進行灰度化、濾波和二值化處理，從而將原始的彩色圖像轉換為理想的二值化圖像。對獲得的二值化圖像進行濾波、填充，然后將螺絲內紋的圖像剪裁，并獲內紋的輪廓圖像。將輪廓的像素信息轉換為坐標信息，對輪廓的坐標進行轉換、分割，并對分割的各部分數據進行曲線擬合。最后，應用人工蜂群算法對每條擬合曲線求最大值并計算各部分的偏轉角度，利用均值濾波減小各部分偏轉角度在求解中造成的誤差。

2 圖像處理

2.1 圖像預處理

在獲取螺絲的原始圖像后，首先將彩色圖像轉換為灰度圖像，從而降低圖像的數據量，減小后續圖像的計算量。灰度化處理一般有：平均值法、最大值法和加權平均值法。這里采用R(0.30)、G(0.59)、B(0.11)的加權平均值法。對轉換后的圖像進行均值濾波，從而對圖像中的高頻噪點進行處理。為了更進一步降低圖像數據量，以減小后續圖像處理的計算量，需要對濾波后的圖像進行二值化處理。圖像的二值化處理不僅減小了圖像數據的大小，也使得圖像的邊緣信息更加清晰。在此采用閾值變化法實現圖像的二值化處理。圖2為螺絲的原始圖像。圖3為二值化圖像。

圖2 原始圖像

圖3 二值化圖像

從圖3可以看出，螺絲內紋的二值化圖像中存在孔洞，會對后續的輪廓提取造成影響。為了避免二值化圖像中存在的噪點，在填充孔洞之前使用中值濾波再進行一次濾波。首先，對處理后的圖像進行取反操作，并對螺絲內紋中的孔洞區域進行填充操作。然后，對填充后的圖像進行邊緣特征的提取，獲取螺絲內紋的邊緣輪廓。最后，將螺絲內紋的輪廓圖從處理后的圖像中剪裁下來并求內紋區域的中心坐標。螺絲內紋輪廓如圖4所示。

圖4 螺絲內紋輪廓圖

2.2 坐標轉換

將圖像的原點平移至內紋的中心坐標以建立新的坐標系，計算當前坐標系下輪廓各像素點的新坐標值。將直角坐標系下的坐標轉換為相對應的極坐標值，得到齒輪輪廓的極坐標集合C(i為坐標點個數)。

C={(r1,θ1),(r2,θ2),...,(ri,θi)}

(1)

極坐標系下的輪廓如圖5所示。將集合C中的坐標序列根據角度ri進行從小到大的排序，獲得新的坐標集合C′。將新的坐標集合C′映射到直角坐標系中，得到如圖6所示的直角坐標系下的輪廓。

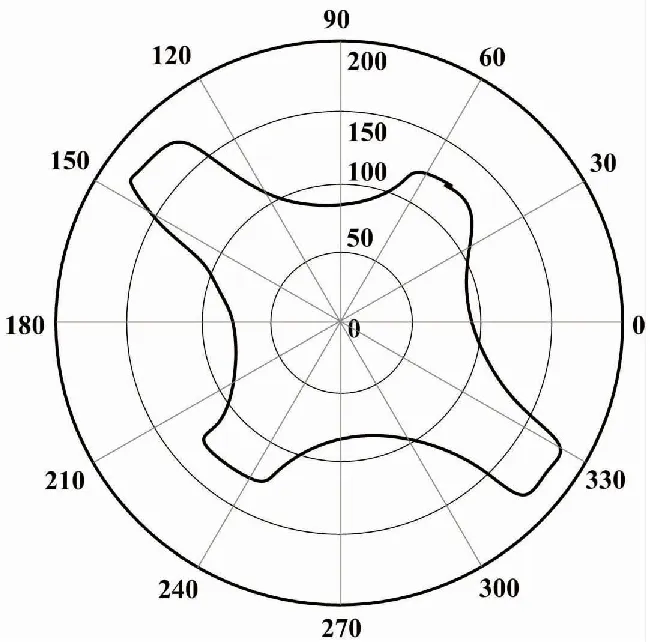
圖5 極坐標系下的輪廓圖

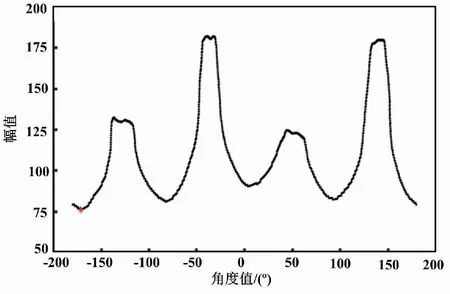
圖6 直角坐標系下的輪廓圖

2.3 坐標數據分割與曲線擬合

本次使用十字形螺絲，內紋的輪廓在直角坐標系中呈現四個波峰。但圖像不符合標準的周期函數圖像，所以采用將坐標數據分割的方法將坐標數據分割為四個單峰波形。單峰波形在曲線擬合中可以采用高斯曲線擬合。

坐標數據的分割中，四個波峰的大致相位差為90°。所以在數據的分割中，首先需要找到一個合適的分割原點。在此，對所有坐標的幅值尋找最小值，將幅值最小值rmin的坐標作為坐標數據的分割原點，將坐標軸上該點左邊的數據平移至數據的末尾，得到新的坐標集合A。

A={(rmin,θmin),(rmin+1,θmin+1),...,(ri,θi),...,

(ri+min-1,θi+min-1)}

(2)

以每90°為一個范圍，將集合A的數據根據角度值進行四等分,得到{A1,A2,A3,A4}。由于每一組數據都是根據角度值進行均分，會導致每一組數據的首個數據或者最后一個數不為最小值的情況。為了保證擬合曲線的二階導數始終小于零，需要對分割后的四個集合進行數據調整，確保擬合出的曲線均為單一的凸函數。

數據調整的主要步驟為：將每一組數據根據角度值分為兩部分，分別求這兩部分幅值的最小值。將前半部分數據中幅值最小值左邊的數據調整至前一個數據集合的尾部，將后半部分數據中最小值右邊的數據調整至下一個數據集合的頭部。

每一組數據呈高斯曲線形式，故在曲線擬合部分采用高斯曲線擬合。為簡化程序設計中初始參數的選取，將四組數據分別平移至第一象限，使每組數據均能使用同一組初始參數進行曲線擬合。本文在將各組數據平移至第一象限內時，將每組數據的第一個數據平移至0°處、同組其余數據平移相同的相位角度，并記錄下每組數據的平移角度(θ1，θ2，θ3，θ4)。調整后的坐標數據如圖7所示。

圖7 調整后的坐標數據圖

根據圖7的數據可以看出，每個波峰部分的數據在幅值上有較大波動。在使用傳統的方法時，需要截取波峰部分的數據，選擇出其最大值或這部分波峰數據的中間數值作為波峰峰值點。截取波峰數據對波峰極值點的選擇有較大的影響，會造成最終得到的偏轉角度有較大的誤差。本文采用了曲線擬合的方法獲取每個波峰的極值點，根據數據的分布選擇高斯曲線擬合，對比一階、二階及高階高斯曲線的效果，在保證曲線的擬合度的情況下選擇三階高斯曲線擬合。擬合函數為：

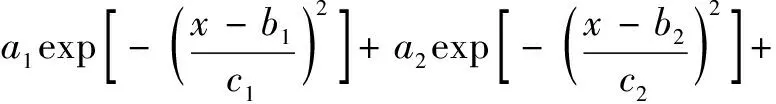
(3)

分別對四組數據進行三階高斯曲線擬合，得到的數據擬合曲線如圖8所示。

圖8 數據擬合曲線圖

3 人工蜂群算法設計

在人工蜂群算法中，蜂群由觀察蜂、采蜜蜂和偵查蜂組成，每個蜜源只對應一個采蜜蜂。當蜜源被采蜜蜂和觀察蜂耗盡時，即在最大搜索次數內無法在找到更優解，采蜜蜂變為偵查蜂，隨機尋找新的蜜源。在人工蜂群算法中主要有三個控制參數：蜜源的數目(采蜜蜂的數量)、最大搜索次數Limit和最大迭代次數maxCycle。

初始時刻所有蜜蜂沒有先驗知識，所有蜜蜂的角色全部為偵查蜂。全局隨機搜索蜜源，得出各自的“收益度”。根據蜜源“收益度”對比，將蜜蜂轉為采蜜蜂和觀察蜂兩類。其中，“收益度”較高的一半轉為采蜜蜂。

①初始時刻，隨機生成N個可行解(X1,X2,...,XNs)。具體隨機產生的可行解Xi為：

(4)

式中:j∈{1,2，…，D}，j為D維解向量的某個分量。

通過分別計算各個向量的適應度函數值并進行排序，適應度值較高的一半作為初始采蜜蜂種群X(0)。

②第n步的采蜜蜂X(n)在當前位置附近的領域范圍內搜索新的蜜源位置。搜索公式為：

(5)

式中：j∈{1,2，…，D}，k∈{1,2，…，N}，N為采蜜蜂個體數量，i≠k，j和k均為隨機生成。

③在采蜜搜索到的新位置向量new_Xi和原位置向量Xi中，采用貪婪選擇算子選取更優適應度的繼承給下一代種群，保證種群進化方向不會后退。其概率分布為：

P{Ts(Xi,new_Xi)=new_Xi=

(6)

④觀察蜂依照采蜜蜂種群適應度值，采用選擇算子計算選擇一個采蜜蜂，并在其領域內進行新位置的搜索。選擇概率為：

(7)

⑤同步驟②和步驟③，記錄下更新后達到的最優適應度值及其相應參數。

⑥當個體采蜜蜂在蜜源周圍搜索次數s達到最大搜索次數,但仍未獲得到更優解，則重新初始化該采蜜蜂的位置。初始化公式為：

Xi(n)=Xmin+rand()(Xmax-Xmin)

(8)

⑦滿足停止條件(iter>maxCycle)，則停止計算并輸出最優解及其相應的參數，否則轉向步驟②。

本文設置初始種群總數30，采蜜蜂數量15，偵查蜂5，最大迭代次數100，最大搜索次數3。根據采蜜蜂數來初始隨機解的數量，通過隨機生成15個角度值，計算得到15個幅值并記錄下其中最大的幅值與角度值。然后計算觀察蜂跟隨采蜜蜂的概率，判斷觀察蜂是否在采蜜蜂所在解的鄰域內尋找新的解求幅值，偵查蜂則在角度值的范圍內隨機生成新的角度值求解幅值。如果求出的幅值為當前最優解，則偵查蜂轉換為采蜜蜂。采蜜蜂在各自當前解的鄰域內搜索新的解，判斷得到的幅值是否更優。當循環三次不能得到更優解時，則采蜜蜂放棄當前解并成為偵查蜂尋找新解。尋找新解的最大迭代次數，即采蜜蜂、觀察蜂、偵查蜂尋找新解的總次數。函數優化曲線如圖9所示。

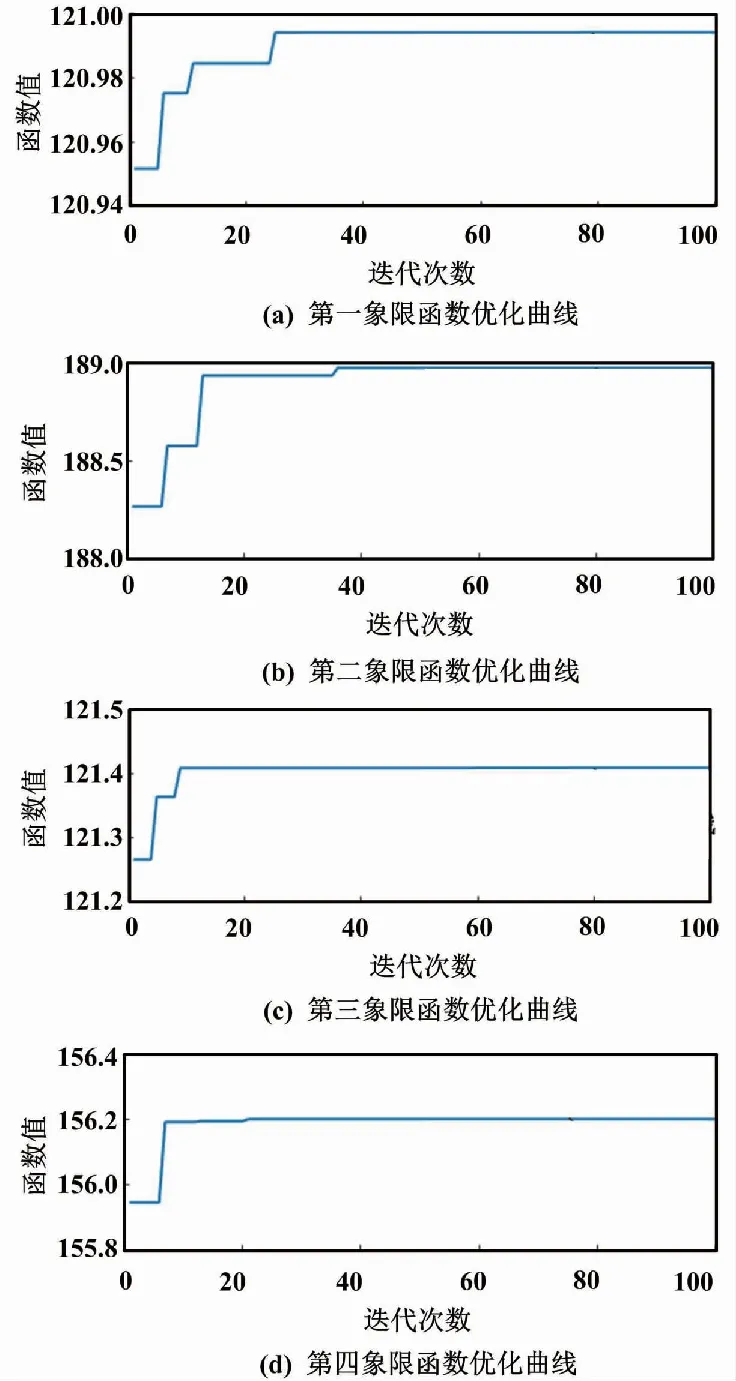
圖9 函數優化曲線圖

4 試驗分析

通過人工蜂群算法，能夠快速求得函數的最大值。在對四個函數的最大值求解過程中，在算法迭代到40次左右就能夠獲取各個擬合函數的最大值。

通過獲取每一部分擬合函數的最大值，確定其相對應的內紋輪廓的峰值位置，即每一部分內紋輪廓的中心點。該中心點與整個螺絲內紋的中心點相連的軸線與X軸正方向所構成的夾角，即為當前內紋的偏轉角度。通過前文中對圖像輪廓進行坐標系的轉換，其相對應的偏轉角度即為幅值最大值相對應的角度值。

φi=θi+ri±90k

(9)

(10)

式中：k的取值根據φi決定。

將φi的取值范圍控制在±45°范圍內，使得偏轉角度控制在最小范圍內，后期在旋轉螺絲刀的姿態中實現最優化。最后通過對獲得的四個偏轉角度進行均值處理。本文測試圖像最終獲得的偏轉角度為38.08°。旋轉效果圖如圖10所示。對原始圖像進行所求偏轉角度的旋轉，可以看出效果較為理想。

圖10 旋轉效果圖

5 結論

本文通過使用圖像處理與人工蜂群算法相結合的方法來實現螺絲當前姿態下的偏轉角度計算：使用圖像處理技術，獲取螺絲內紋的輪廓，并將輪廓數據進行轉換與函數擬合；利用人工蜂群算法，對擬合出的函數進行尋優，最終獲取當前姿態下的偏轉角度。本方法結合了圖像處理的精度高與人工蜂群算法計算量小、快速獲取全局最優的特點，計算出精度較高的偏轉角度。同時，該方法有較好的拓展性，適用于各種類型的螺絲內紋的偏轉角度計算。