基于場景削減的網源協同規劃研究

王華勇，傅 強,徐 昱,王梓萌

(1.南瑞集團有限公司國網電力科學研究院有限公司，江蘇 南京 211106；2.國電南瑞科技股份有限公司，江蘇 南京 211106)

0 引言

日益嚴重的能源危機以及化石能源帶來的環境問題，迫使各國加快能源結構轉型。風電和光伏發電易受地理位置和氣候條件影響，源端具有很強的不確定性。傳統的電力系統規劃模式無法考慮不確定性因素帶來的影響。場景分析法是該問題的主要處理方法。隨著電力系統規模的不斷擴大及間歇性能源的大規模并網，場景數量呈爆發式增長。如何同時滿足求解精度與求解效率的需求，是場景分析法應用于電網規劃的關鍵問題。場景集中存在大量相似場景。場景削減通過各種方法減少相似場景。文獻[1]從一年8 760個場景中選取P個風電出力較大場景以及Q個負荷較大場景構成(P+Q)個典型場景。文獻[2]將負荷峰谷差最大一日作為典型場景。但無論是典型日法，還是平均值法，都忽視了場景集內數據的變化規律，在一定程度上破壞了場景集的原有特征。

后向削減法(backward reduction，BR)、場景樹構建法(scenario tree construction，STC)、快速前向選擇法(fast forward selection，FFS)和各種聚類分析法[3-4]，可以在保持場景集原有特征的前提下實現場景削減。相較于BR、FFS和STC，聚類分析法原理簡單、時間復雜度低。文獻[5]應用聚類分析法進行負荷曲線分類。文獻[6]通過聚類分析法形成具有代表性的儲能單元充放電曲線。文獻[7]通過聚類分析法生成風電/光伏典型場景。上述聚類分析法的研究對象都是性質單一的負荷、風電、光伏或儲能場景，但在生產活動中它們往往表現出一定的相關性。因此，在制定電力系統規劃方案時，考慮三者的相關性，可以有效提升方案的經濟效益與合理性。

為滿足整體方案的經濟效益與安全性，本文建立了網源協同雙層規劃模型。現有的網源協同規劃模型[8-10]較少考慮風電機組和光伏發電機組可信容量對系統備用容量的貢獻。因此，上層模型以各種成本最小為目標，并加入風光發電聯合系統容量可信度參數，考慮系統的充裕性；下層模型采用N-1準則和節點支線數量約束，提升規劃后系統的安全性。針對傳統K-medoids算法的缺陷，本文對其進行了調整，以此獲得聚類場景，并結合選取的極端場景共同構造典型場景集。根據典型場景集求解網源協同雙層規劃模型，獲得綜合考慮風、光、負荷不確定性與相關性，以及系統經濟性與安全性的網源協同規劃方案。

1 典型場景集構造

1.1 基于K-medoids的聚類場景

相較于K-means算法，K-medoids算法避免了特殊值帶來的影響，噪聲敏感度低。因此，本文選擇K-medoids算法對大規模場景進行削減處理。同時，針對K-medoids算法的缺陷，對算法流程進行調整。

1.1.1 聚類個數的確定

如式(1)所示，計算不同K時的CH值。CH最大時對應最佳聚類場景個數K。

(1)

式中：SW為每類的協方差矩陣；SB為各類間的協方差矩陣；K為聚類場景個數；n為場景總數；Tr為矩陣的跡。

1.1.2 聚類中心的選取

場景m到聚類場景cj的相似程度計為d(xm,cj)，值越小，代表場景越相似。根據式(2)選取新的聚類場景。

(2)

式中：CP為聚類場景cP所屬類的所有場景:xm為CP中的一個場景。

調整后的K-medoids算法基本步驟如下。

(1)設置聚類場景個數K的搜索范圍為(1～20)。

(2)在搜索范圍內，步驟如下。

①從場景集中選取一個場景作為首個聚類場景，記為c1。

②按照式(2)，從場景集中確定第j個聚類場景cj(j≥2)，離原先聚類場景最遠的場景被選為新聚類場景的可能性最大。

③計算場景集中各場景到聚類場景的相似程度d：根據d最小原則，將各場景重新劃分至新聚類場景代表類中。

④在每個類中，選取不同場景代替已有聚類場景，并計算本類其他場景到代替場景的相似程度d；按照d總和最小原則確定本類的新聚類場景。

⑤不斷更新聚類場景，直至聚類場景不再改變。

(3)比較不同K時的CH值，CH值達到最大時的K為最佳聚類個數。

(4)輸出最佳聚類結果。

1.2 極端場景選取

基于場景削減的網源協同規劃方法是為了實現計算精度與計算效率的有效平衡。雖然通過K-medoids算法可以獲得少量具有代表性的聚類場景，減少了計算量，但一定程度上忽視了計算精度。因此，通過選取以下幾類極端場景，共同構造能夠代表所有場景的典型場景集。

首先，選取各簇族中距離聚類場景最遠的樣本作為第一類極端場景。

其次，負荷最大時刻、負荷最小時刻、光伏出力和風電出力總和與負荷相差最大時刻、負荷與光伏出力和風電出力總和相差最大時刻是電力系統運行過程中存在的典型特殊場景。令負荷為fs、光伏出力為PV,s、風電出力為PW,s，則四類極端場景如式(3)～式(6)所示。

①負荷最大時刻為:

Ts1=max(fs)

(3)

②負荷最小時刻為:

Ts2=min(fs)

(4)

③光伏出力和風電出力總和與負荷相差最大時刻為:

Ts3=max(PV,s+PW,s-fs)

(5)

④負荷與光伏出力和風電出力總和相差最大時刻為:

Ts4=max(fs-PV,s-PW,s)

(6)

2 網源協同規劃雙層模型

2.1 上層規劃模型

2.1.1 目標函數

目標函數如式(7)所示，即式(8)輸電線路年建設成本、式(9)電源年建設成本、式(10)電源年運行成本、式(11)棄風懲罰成本和式(12)棄光懲罰成本總和最小。

minf=fl+fg+fgo+fwind+fpv

(7)

①輸電線路年建設成本。

(8)

式中：cijk和nijk分別為節點i和節j點之間第k條線路的投資成本以及0-1決策變量；Ωc為待選線路集合；x為貼現率；y為輸電線路經濟使用年限。

②電源年建設成本。

(9)

式中：ci,k和ni,k分別為節點i第k個發電機組的投資成本以及0-1決策變量；Gc為待選發電機組集合；x為貼現率；y為發電機組經濟使用年限。

③電源年運行成本。

(10)

式中：oi,k和gi,k,s分別為節點i第k個發電機組在場景S下的單位運行成本和出力；ws為場景S的等效年運行時間。

④棄風懲罰成本。

(11)

式中：cwind為單位棄風懲罰成本；ws為場景S的等效年運行時間；Pwind,i,j,s為風電場j在場景S下的實際出力。

⑤棄光懲罰成本。

(12)

式中：cpv為單位棄風懲罰成本；ws為場景S的等效年運行時間；Ppv,i,j,s為光伏電場j在場景S下的實際出力。

2.1.2 約束條件

①決策變量約束。

(13)

(14)

式中：nijmax和nimax分別為節點i和節點j之間最大可建輸電線路條數和節點i待選發電機組臺數；0為規劃年不新建輸電線路或發電機組；1為規劃年新建輸電線路或發電機組。

②節點有功功率平衡約束。

(15)

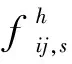
③已有支路直流潮流約束。

(16)

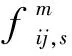
④待選支路直流潮約束。

(17)

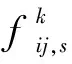
⑤已有輸電線路容量約束。

(18)

式中：fijmax為節點i和節點j之間輸電線路的最大傳輸功率。

⑥待選輸電線路容量約束。

(19)

⑦已有發電機組出力約束。

(20)

式中：gi,m,s為節點i第m個已有發電機組在場景S下的出力。

⑧待選發電機組出力約束。

(21)

式中：gi,k,s為節點i第k個待選發電機組在場景S下的出力。

⑨發電機組年發電量約束。

(22)

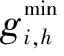
⑩母線相角約束。

(23)

θref=0

(24)

(25)

式中：Gc為已建及待建常規發電機組集合；Gx為已建及待建風電或光伏機組集合；ah為風光聯合發電系統可信容量度；r為系統備用率。

上層規劃模型采用YALMIP工具包進行編寫，通過Gurobi進行求解。

2.2 下層規劃模型

2.2.1 目標函數

下層規劃以上層規劃結果為基礎，以系統無切負荷為目標函數，通過斷線約束對上層規劃建設結果進行(N-1)校驗，判斷已建及待建線路是否滿足(N-1)準則。根據(N-1)校驗結果，選擇引起系統切負荷最嚴重的輸電線路作為新的約束條件加入上層規劃模型。下層規劃的目標函數如式(26)所示。

(26)

式中：Rd,i為負荷水平為d時節點i的切負荷量。

2.2.2 約束條件

首先，添加斷線約束進行輸電線路N-1校驗。然后，針對因輸電線路功率越限導致的系統切負荷，通過添加新的輸電線路容量約束考慮輸電線路N-1準則，同時新增節點支線數量約束增大系統可靠性。下層規劃約束條件如式(27)～式(29)所示。

(27)

(28)

Ωj/i≥2

(29)

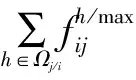
將新增約束條件代入上層規劃模型，通過上層規劃模型求出新的網源協同規劃方案，再進行輸電線路N-1校驗，直至系統沒有切負荷，且所有節點有兩條以上輸電線路連接。

3 算例分析

3.1 Garver-6系統網源協同規劃

修改后的Garver-6節點系統共有15條輸電走廊。Garver-6節點系統如圖1所示。已建圖1所示輸電走廊6條。待建走廊9條，每條走廊最多可建3條支線。5組負荷分別位于節點1、2、3、4、5；風電場位于節點2，裝機容量為85 MW；光伏機組位于節點3，裝機容量為85 MW。

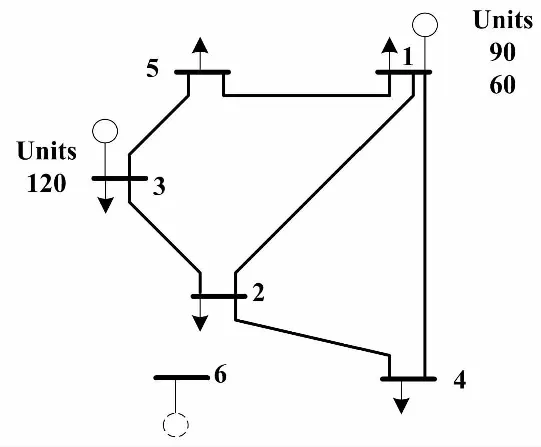
圖1 Garver-6節點系統示意圖

本節采用的5組負荷數據、1組風電出力數據、1組光伏出力數據來源于文獻[11]。首先，按照四季對8 760日負荷、風電和光伏出力歷史數據進行初始劃分，得到春夏秋冬4組數據。然后，通過K-medoids算法分別對4組數據進行聚類削減。最后，結合極端場景構造典型場景集，分別進行考慮負荷與風電出力相關性、負荷與光伏出力相關性及負荷/風電/光伏出力三者相關性的網源協同上層規劃。單位棄風懲罰成本取0.15萬元/MWh。貼現率取7%，輸電線路和電源經濟使用年限均取25年，系統備用率取20%，母線相角差取0.6。

算例1 考慮負荷、風電和光伏出力之間的相關性，風光出力按風光聯合發電系統容量可信度31.80%計算。

以算例1的規劃結果為基礎，進行考慮輸電線路N-1的網源協同下層規劃。算例1規劃新建5條支線，加上6節點系統原有支線，共計11條支線。分別通過添加輸電線路容量約束和斷線約束考慮輸電線路N-1。系統最大切負荷量如表1所示。

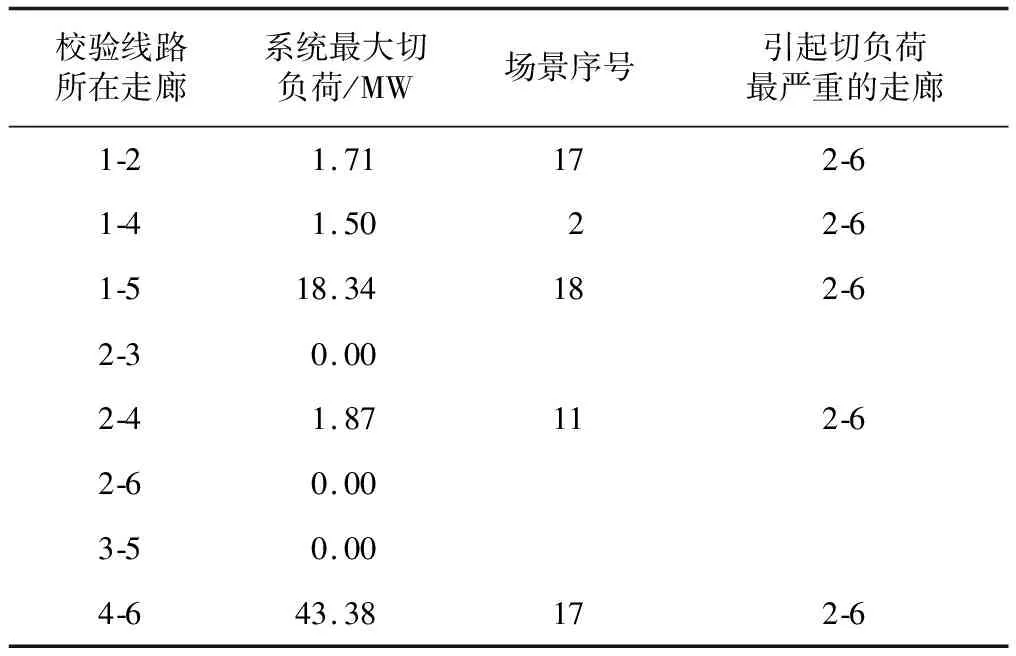
表1 系統最大切負荷量

根據表1，當走廊4-6一條支線斷線后，走廊2-6的功率越限43.38 MW，系統最大切負荷量為43.38 MW。因此添加新的輸電線路容量約束，如式(30)所示。走廊2-6引起系統嚴重的切負荷，因此添加斷線約束，如式(31)所示。

(30)

(31)

分別將式(30)和式(31)作為約束條件，代入上層規劃模型進行求解。Garver-6系統規劃結果如表2所示。

表2 Garver-6系統規劃結果

算例1是上層規劃，算例2、3是下層規劃。對比算例1、2、3的規劃結果：算例2較算例1在走廊3-6多新建了1條支線，電源建設方案保持一致，電網建設成本增加0.03億元；算例3較算例1在走廊3-6多新建了2條支線，電源建設方案保持一致，電網建設成本增加0.06億元。

對比算例2和算例3的規劃結果：算例3較算例2在走廊3-6處多新建一條支線。雖然算例2和算例3都滿足了輸電線路N-1，但算例2的建設規模和建設成本都小于算例3，說明當因輸電線路功率越限導致切負荷時，通過添加新的輸電線路容量約束得到的規劃方案，比通過添加斷線約束得到的規劃方案具有更高的經濟效益。

3.2 巴西南部46節點系統網源協同規劃

巴西南部46節點系統[12]如圖2所示。已建輸電線路62條，可擴建/新建輸電走廊79條，每個輸電走廊最多可建4條輸電線路。系統已建機組26臺，其中常規機組10臺。

圖2 巴西南部46節點系統示意圖

負荷、風電出力和光伏出力數據來源于文獻[11]，共計19組全年時序負荷，4組全年風電時序出力。4組全年光伏時序出力，19組負荷分別位于節點2、4、5、8、12、13、20、22、23、24、26、33、35、36、38、40、42、44和45。4個風電場分別位于節點32、37、39和46，裝機容量分別為70 MW、140 MW、160 MW、140 MW。4個光伏電場分別位于節點24、28、30和34，裝機容量分別為100 MW、80 MW、120 MW、150 MW。風光聯合發電系統容量可信度為18.02%。

考慮負荷、風電出力和光伏出力三者相關性的典型場景集網源協同規劃結果如表3所示。

表3 典型場景集網源協同規劃結果

對比算例4和算例5的規劃結果，先進行電源規劃、后進行輸電網規的網源不同步規劃的方法，雖然在電源建設成本上相對較少，但是其電網建設成本和電源運行成本都較網源協同規劃高，總成本高0.19億元。這說明相較于傳統的網源不同步規劃，網源協同規劃具有更好的經濟效益。

3.3 典型場景集有效性分析

為了驗證本文所用方法，即通過典型場景集進行網源協同規劃的正確性與優越性，以天為單位采用全年365天的場景進行全場景分析。分析采用不考慮N-1，但考慮負荷、風電和光伏出力相關性的算例6。分別從規劃方案和運算時間兩個方面，對全場景分析法和本文所用方法進行對比分析。典型場景集有效性分析如表4所示。

表4 典型場景集有效性分析

對比算例1和算例6的規劃結果，兩個算例的電源建設方案和電網建設方案保持一致，表明了本文采用典型場景集用于網源協同規劃的正確性；而算例6的平均運行時間是算例1的8倍，說明本文所使用的方法不僅正確，而且計算效率較全場景分析法更高。

4 結論

本文通過調整K-medoids算法流程，得到聚類場景，并結合選取的極端場景共同構造了典型場景集，并以此求解網源協同雙層規劃模型。上層模型以各種成本最小為目標，同步考慮系統的充裕性；下層模型考慮規劃后系統的安全性。以修改的Garver-6和巴西南部46節點網架為平臺開展算例驗證，得出以下結論。

①當因輸電線路功率越限導致切負荷時，通過添加斷線約束得到的規劃方案更具經濟效益。

②在新能源大規模并網的背景下，采用網源協同規劃較網源不同步規劃具有更好的經濟效益。

③在電力系統規模不斷擴大和間歇性能源大規模并網的背景下，本文所用基于場景削減的典型場景集構造法，能夠有效地對大規模場景進行處理分析，實現了計算精度與計算效率的平衡。