基于改進變學習率神經網絡的風電機組故障預測研究
陳思羽,王國新,張冬妮
(黑龍江科技大學 電氣與控制工程學院,哈爾濱150022)
0 引 言
傳統的風電故障檢測是先通過Relief算法對風電系統數據進行特征參數權重計算,然后通過權重系數排名選擇適當的參數,利用BP神經網絡對當前傳感器采集的各種數據進行分類,通過傳統的神經網絡進行非線性映射[1]。由于傳統的BP神經網絡參數眾多,計算和訓練過程緩慢,在大型風電機組中因為參數繁多使得訓練時間更加緩慢,所以改進優化方法或者使用其它網絡結構就變的尤為重要,此前文獻[2]和文獻[3]中運用的個體變學習率和整體變學習率算法由于算法比較簡單,存在一定優化空間。通過對個體和整體變學習率的算法進行優化調整,以達到更快的收斂速度和更短的訓練時間。將優化后的改進BP神經網絡應用于風電機組故障預測,通過試驗證明該算法在風電機組故障診斷中具有較好的適用性,與傳統方法相比進一步減少了訓練時間。
1 BP神經網絡原理
在機器學習中,神經網絡算法是基礎,其結構如圖1所示。
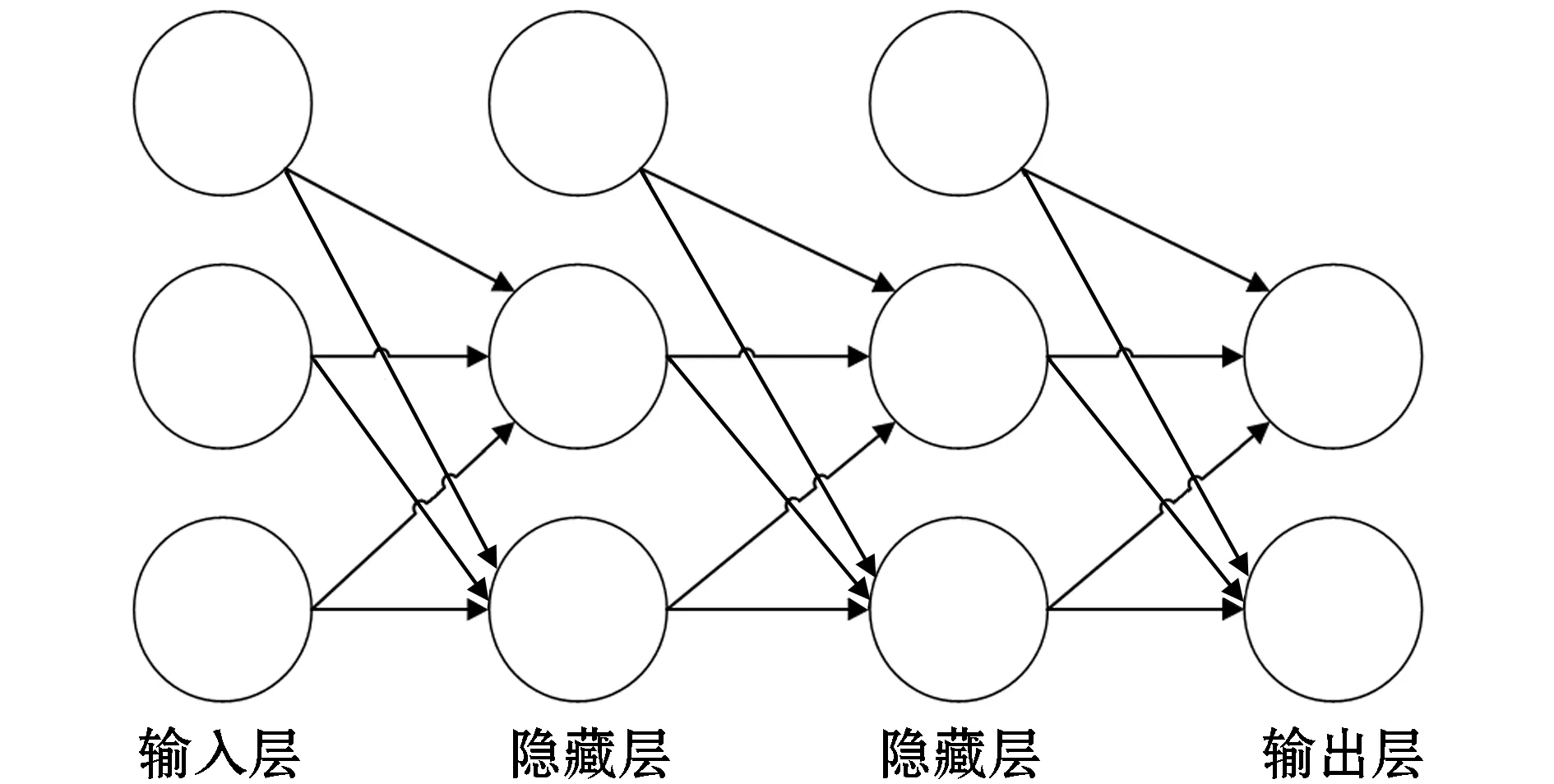
圖1 BP神經網絡結構
BP神經網絡由輸入層、隱藏層和輸出層組成[4],其運算過程主要分為前向傳播和反向傳播。前向傳播是輸入層通過輸入樣本x及參數w(1)、b(1)到隱藏層[5],求得z(1),進而求得a(1);再將參數w(2)、b(2)和a(1)一起輸入輸出層求得z(2),通過激活函數求得a(2);最后得到損失函數L(a(2),y)這個過程稱為前向傳播,圖2為前向傳播示意圖。訓練過程中計算誤差和實際誤差的差值稱為損失函數。在訓練過程中需對損失函數進行梯度下降計算,在此計算過程中需要從后往前依次求各個參數的偏導即反向傳播。

圖2 前向傳播
前向傳播過程:
z(1)=w(1)C+b(1)
a(1)=g(z(1))
z(2)=w(2)a(1)+b(2)
a(2)=σ(z(2))=sigmoid(z(2))
L(a(2),y)=(y-1)log(1-a(2))-yloga(2)
sigmoid函數的導數為
反向傳播過程:
=dz(2)·w(2)×g′(z(1))
=dz(1)·XT
2 改進變學習率算法
雖然文獻[1]和文獻[2]針對BP網絡訓練慢的問題提出個體變學習率算法和整體變學習率算法,但是變學習率算法仍然存在優化和改進空間,因此提出變學習率算法的改進方法。
2.1 變學習率算法
2.1.1 個體變學習率
輸入層與隱藏層的權值矩陣用符號aij來表示,學習速率矩陣設為η,則權值aij所對應的學習率為ηij[6]。aij(n)為權值aij經過n次迭代后得到的值,則ηij(n)對應的學習率是aij(n),E(n)是第n次迭代后得到的全局誤差。現有的個體變學習速率迭代式為
2.1.2 整體變學習率
隱藏層與輸出層的權值矩陣為bjk。η是初始學習速率矩陣,范圍為[0,1],η(n)代表第n次的學習速率,E(n)代表第n次迭代的全局誤差。整體學習速率的動態調節規則為
2.2 改進變學習率算法
由于現有變學習率算法不夠完善,因此提出一種改進變學習率算法,用兩次迭代的代價函數差值的正負決定步長變化項的正負,結合差值的大小,確定步長的變化幅度。變化的步長使用代價函數差值的對數值作為變化的倍數,當系統快速收斂時,快速調整系統的學習速率,當系統緩慢收斂時,緩慢調整系統的學習速率,以增加收斂速度,減少振蕩的可能性。
2.2.1 改進個體變學習率
改進的個體變學習率算法將輸入層與隱藏層的權值矩陣設為aij,學習速率矩陣設為η,則權值aij所對應的學習率為ηij。aij(n)為權值aij經過n次迭代后得到的值,則ηij(n)對應的學習率是aij(n),E(n)是第n次迭代后得到的全局誤差。Sde為步長調節系數,改進變學習率調節方法為
η(n+1)=η(n)+lg(E(n)-E(n-1)+1)×Sde
當第n次迭代的誤差E(n)小于第(n-1)次的迭代誤差時,代表系統收斂,則學習率增量為正,(n+1)次的學習速率等于η(n)加上正數,則學習率增大,反之學習率減少。這樣反復調節aij的學習速率,直至全局誤差小于目標值。
2.2.2 改進整體變學習率
隱藏層與輸出層的權值矩陣用符號bjk表示,η為其初始學習速率矩陣,其取值范圍是[0,1],η(n)代表第n次的學習速率,E(n)代表第n次迭代的全局誤差。改進整體學習速率的動態調節規則為
η(n+1)=η(n)+lg(E(n)-E(n-1)+1)×Sde
當第n次迭代的誤差E(n)小于第(n-1)次的迭代誤差時,代表系統收斂,則學習率增量為正,(n+1)次的學習速率等于η(n)加上正數,則學習率增大,反之學習率減少。這樣反復調節bjk的學習速率,直至全局誤差小于目標值。
對于閾值矩陣也采用上述方法進行調節。
3 改進變學習率算法風電故障檢測
3.1 數據特征描述
風電機組運行過程中的主要參數包括功率因數設定值、機航位置、塔架加速度、傳動系統加速度、機艙旋轉等[7],需將各參數數據整理為數據庫格式并清楚標記出故障數據。由于參數眾多,這里使用Relief算法對原始數據的參數進行權重計算,通過排名選擇特征參數權值排名較高的參數。表1為權重計算后權重大小排名前10名的參數。

表1 特征參數權重排名Table 1 Weight ranking of characteristic parameters
經過Relief篩選后的風電機組運行數據具有一定的物理意義,由于各參數單位之間的差異性,使得各項參數在數值大小上具有很大的差異,為防止一些數值較小的參數被數值較大的參數湮滅,就需要對參數進行歸一化計算,將其折算到[0,1]區間內。
3.2 風電故障預測的數學建模
3.2.1 數據預處理
風電系統運行狀態量有140個,通過Relief算法將其縮減為50個,并對其進行歸一化計算。其數學表達式如下:
Xop=normalize(Relief(Xorg))
式中:Xorg為從風電機組管理系統中直接獲得的維度為140的風電機組狀態量;normalize(x)為歸一化算法;Xop為經過預處理后的狀態量。
3.2.2 神經網絡選擇及其數學模型
測試網絡使用50輸入、1輸出、10個隱節點的神經網絡,其輸出函數表達式為
式中:bn為隱藏層到輸出層的偏置值;B為輸入層到輸出層的偏置值;Wn為輸入層到輸出層權值;win為隱藏層到輸出層權值;tansig函數為測試網絡的隱層傳遞函數。
3.2.3 目標函數
定義神經網絡損失函數的數學表達式:

3.2.4 數學模型的求解
風電故障檢測為分類問題,網絡模型的代價函數值越小越好,其數學表達式如下:
(1)
數學模型求解的目標是對神經網絡的權值矩陣進行優化。在不滿足收斂判定條件和最大訓練次數限制的情況下,持續進行梯度下降迭代。式(1)中第三項為最大訓練次數限制,第二項為收斂判定條件。
3.3 訓練結果對比及說明
圖3為標準BP神經網絡誤差隨訓練循環次數變化曲線,可以看出,當迭代次數達到1 000次(最高循環次數限制)時達到最小誤差。

圖3 標準BP神經網絡誤差
變學習率BP神經網絡的代價函數值與訓練次數之間的關系如圖4所示,當迭代次數達到125次時代價函數值最小,與標準網絡相比訓練次數大幅度減少。

圖4 變學習率BP神經網絡誤差
算法改進后的變學習率BP神經網絡誤差和迭代次數之間的關系如圖5所示,該網絡誤差在第93個循環時達到最小,相比變學習率BP神經網絡訓練減少32個周期。

圖5 改進變學習率BP網絡誤差
標準網絡、變學習率網絡和算法改進后的變學習率網絡訓練結果對比如表2所示。與變學習率網絡相比,改進變學習率網絡訓練循環次數減少27%,雖然訓練精度略有下降,但改進變學習率網絡明顯縮短了模型訓練時長,提升了效率。綜合分析訓練結果得出改進后的算法適合對訓練速度要求較高而對于訓練精度的下降有一定容忍的場合。

表2 三種算法的訓練結果
4 結 語
提出一種運用于風電機組故障檢測的改進變學習率BP神經網絡,通過計算最近兩次訓練的誤差的差值來動態調節BP神經網絡的訓練步長,以達到縮短訓練時間、提升訓練誤差的收斂速度的目的。
通過對改進變學習率BP神經網絡與變學習率BP神經網絡和標準BP神經網絡的誤差隨訓練循環次數變化情況的曲線進行對比,并運用實際的風電機組運行數據對改進變學習率BP神經網絡的收斂性能進行驗證,一方面證明了改進變學習率算法相比變學習率算法可以縮短訓練時間,另一方面證明了改進變學習率BP神經網絡對于風電機組故障檢測的適用性。

