油田注水離心泵大修閾值確定方法研究

毛仲強，秦天飛，柳 楠，段禮祥

（1.中國石油塔里木油田分公司，新疆庫爾勒 841000；2.中國石油大學（北京）安全與海洋工程學院，北京 102249）

0 引言

油田現場離心泵內部零部件種類繁多，關系復雜，每種零部件都有其特定的失效方式。目前針對離心泵退化的研究多是集中在零部件方面[1-2]，而對離心泵整體退化特征的研究較少。正因為離心泵的退化特征具有復雜性，單一零部件的特征指標或單一特性參數并不能完整地反映離心泵運行過程中的退化情況。因此，構建能夠表征離心泵整體健康狀態的退化指標是十分必要的。

目前通用的離心泵大修標準設定方法，都是根據維保規程或經驗設置為固定的靜態時間閾值，沒有考慮到實際運行情況，使得大修標準閾值與狀態變化無關[3-4]。然而離心泵運行狀態是受多種因素影響的，若采用相同的判定標準判斷是否應該進行大修顯然是盲目的。

針對上述問題，本文提出了基于KPCA（Kernel Principal Component Analysis，核主成分分析）和GA-PSO-PNN 的離心泵大修閾值模型。將離心泵振動指標和特性參數指標組成多源特征集，利用KPCA 進行特征融合得到離心泵退化指標，通過KPCA 降維優化PNN（Probabilistic Neural Network，概率神經網絡）結構，通過GA-PSO（Genetic Algorithm-Particle Swarm Optimization，遺傳粒子群算法）優化PNN 平滑因子，基于優化PNN建立離心泵大修閾值模型，進而建立動態大修閾值曲線，能夠及時判斷離心泵是否應該進行大修。

1 退化指標構建

1.1 故障統計分析

對某油田注水站離心注水泵機組統計歷史故障監測詳情如表1 所示，從中可以總結得出：

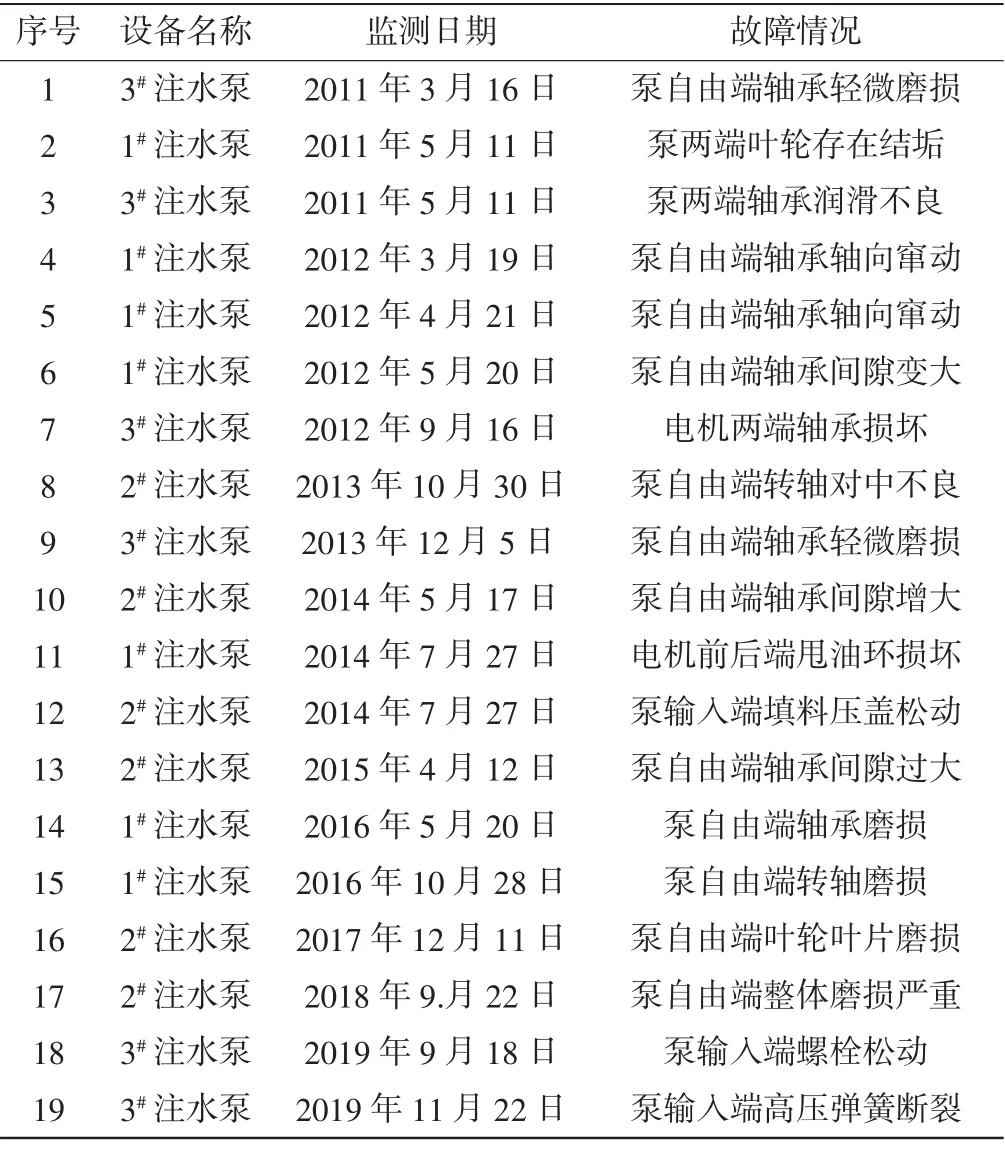
表1 歷史故障匯總

（1）離心泵泵體故障約占故障總數的89.5%，且故障部位為泵自由端的約占故障總數的73.7%（由此看出，離心泵自由端為故障多發的敏感部位）。

（2）離心泵故障部件為泵軸、葉輪、軸承等關鍵零部件，這些零部件之間的安裝方式、連接形式、相互作用機制等會影響退化過程和失效模式，共同決定了離心泵的健康狀態和剩余壽命。

這些關鍵零部件之間的安裝方式、連接形式、相互作用機制等會影響退化過程和失效模式，共同決定了離心泵的健康狀態和剩余壽命。

1.2 特征指標提取

根據國際標準及我國振動標準，選取振動速度有效值和振動位移峰峰值分別作為評估離心泵軸承和泵軸退化狀態的振動指標。

對于離心泵葉輪葉片在故障狀態下的損壞，葉片在相應側的通過頻率就會顯示出來。因此，葉片通過頻率幅值可以有效評估離心泵葉輪的退化狀態。

離心泵流量和壓力性能的退化是離心泵固有的退化特性，流量不變時離心泵的失效形式具體表現為出口壓力降低，因此可以將離心泵出口壓力作為一項重要的退化性能指標。

1.3 多源特征融合

KPCA 是對線性PCA（Principal Component Analysis，主成分分析）進行擴展，利用非線性方法提取主成分，常用來進行特征提取和降維，在模式識別領域中應用廣泛（圖1）。

圖1 KPCA 原理

振動速度有效值、振動位移峰峰值、葉片通過頻率幅值表征離心泵的振動，出口壓力值表征離心泵的性能，經KPCA 多源特征融合后得到第一核主成分作為離心泵退化指標，用來定量表征離心泵整體的退化狀態。

2 大修閾值研究

2.1 概率神經網絡

概率神經網絡PNN 是由概率統計理論和基于貝葉斯的分類網絡兩部分組合而成[5]，具有結構簡單、訓練快速的優點。PNN結構有4 層，分別為輸入層、模式層、求和層、輸出層。

2.2 結構優化

使用樣本數據進行網絡訓練，首先需要估算條件概率P（X∣fi），其估計函數表達式為：

其中，m 表示向量維數，X 和xi分別表示識別樣本以及模式樣本向量，σ 為平滑因子，為分類模式的數量。

經KPCA 特征融合后得到的退化指標是一維向量，將維數m=1 代入式（1）中得到：

其中，xi是第i 個樣本值，N 是樣本總數，x 是待識別的樣本指標。

KPCA 特征融合降低了PNN 網絡結構的復雜度，優化后得到的PNN 結構簡單。起始層執行設備數據預處理，模式層則不會改變其中的樣本點，僅需要估計激活函數的平滑因子，然后樣本層中依據式（2）計算每一樣本點下的條件概率，求和層將其累加起來，根據求和層得到的結果建立設備的狀態概率模型。

2.3 平滑因子優化

PNN 的平滑因子即為標準差。如果其樣本層節點不變，則平滑因子與整個概率密度分布函數的變化有關。若平滑系數過小，則只能當成訓練樣本的隔離函數，此時PNN 等效于最近鄰域分類器；若平滑系數過大，PNN 此時不能完全區分細節，其作用更像是線性分類器。因此，為提高PNN 模型的有效性和容錯能力，需要優化平滑因子。

本文采用結合遺傳算法及粒子群算法而成的遺傳粒子群算法（GA-PSO）優化PNN 的平滑因子。GA-PSO 算法的核心思想是將GA 算法中的變異操作引入到PSO 中，通過對PSO 算法中的慣性權重與加速因子進行改進，使其具有更好的優化性能和更強的抗干擾能力[6]。

2.4 大修閾值確定

本文采用格拉布斯準則作為大修閾值的確定準則，置信概率設定為90%，根據正常及故障數據建立狀態概率模型，將概率累計分布函數值達到90%處的閾值作為故障報警閾值，在此基礎上進一步將大修閾值設定為：

其中，X 為大修閾值，x（P=90%）為概率累計分布函數值達到90%處的退化指標閾值，閾值因子k=1.5，p 為比例系數，取20%。

基于KPCA 和GA-PSO-PNN 的離心泵大修閾值模型具體實現流程如下：

（1）利用KPCA 對離心泵多源特征集進行特征融合，得到退化指標作為PNN 的輸入數據。

（2）利用KPCA 降低原始數據維數，優化PNN 網絡結構。

（3）設置相關參數，采用GA-PSO 算法優化PNN 的平滑因子。

（4）將退化指標數據輸入到優化PNN 模型中建立離心泵狀態概率模型。

（5）根據格拉布斯準則確定離心泵大修閾值，形成自適應的動態大修閾值曲線。

3 實例分析

本文采用某油田注水站離心泵監測數據進行分析，監測數據包括振動數據和壓力數據，經查詢和計算可得振動速度有效值、振動位移峰峰值、葉片通過頻率幅值以及出口壓力值4 種離心泵原始特征指標數據（表2）。

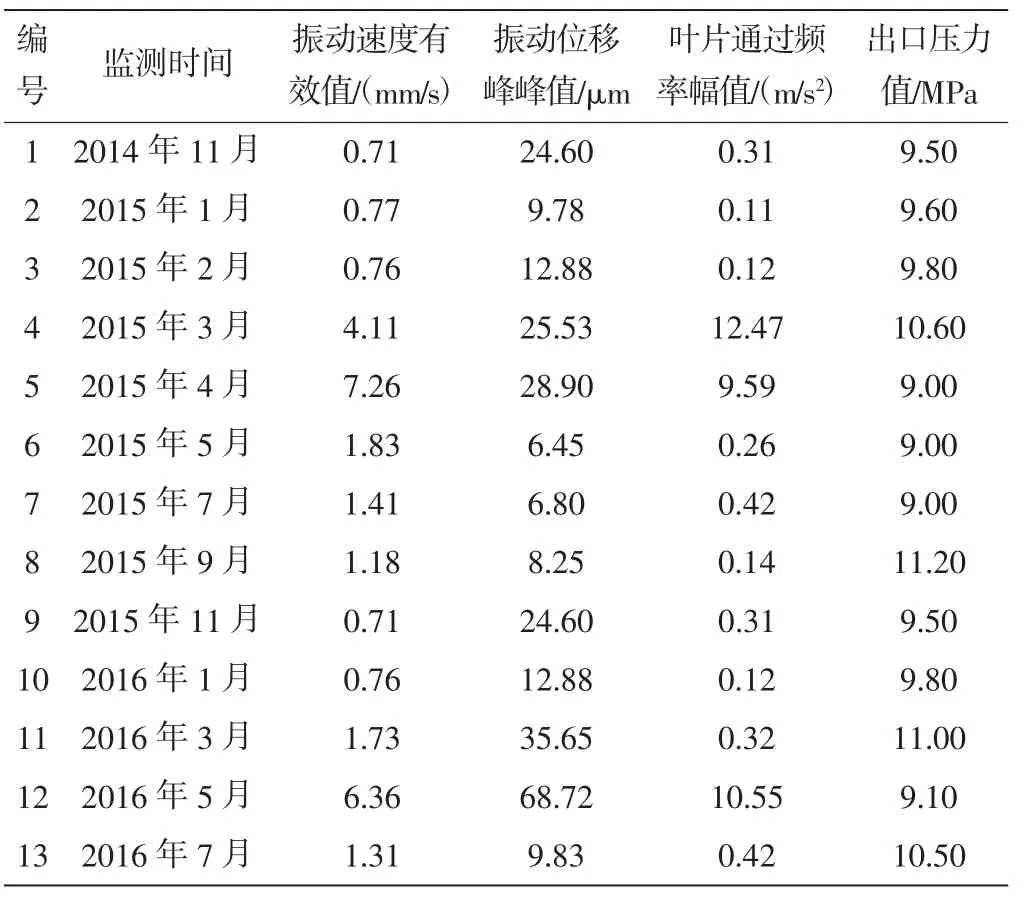
表2 原始特征指標值

首先以原始特征作為樣本數據采用GA-PSO 算法進行PNN 平滑因子尋優。原始數據按離心泵狀態可分為三類：正常、異常和故障。選取編號2、4、5 的數據作為測試樣本，其余作為訓練樣本，建立的PNN 網絡結構為4-10-3-3。其中，第一個數字表示原始特征維數是4；第二個數字表示訓練樣本組數為10；最后兩個數字表示離心泵正常、異常、故障的3 種狀態。初始化GA-PSO 算法的參數，設定種群大小為20，加速因子為2，最大迭代次數為100，慣性權重為0.2，交叉概率為0.7，變異概率為0.3，加速因子和慣性權重隨迭代次數線性變化。

選取訓練樣本均方誤差作為適應度函數，采用GA-PSO 算法對平滑因子進行優化，經過多次迭代后找出最佳適應度下的平滑因子。為說明其優越性，將GA、PSO、GA-PSO 三種算法優化下的均方誤差進行對比分析，結果如圖2 所示。

圖2 均方誤差變化曲線對比

由圖2 可知，GA-PSO 算法不容易陷入局部最優，能收斂于更小的最佳適應度值0.219 4，其尋優精度高于其他兩種算法，所以采用GA-PSO 算法優化PNN 網絡能獲得比普通算法更好的結果。

GA-PSO 算法在最佳適應度為0.219 4 的條件下得到最優平滑因子為0.753 8。

確定最優平滑因子后，采用KPCA 降維對PNN 網絡結構進行優化。將表2 所示的原始指標數據進行KPCA 特征融合，提取融合后的第一核主成分指標作為無量綱的離心泵退化指標，同時作為大修閾值模型的輸入數據。融合后得到的離心泵退化指標趨勢如圖3 所示。

圖3 離心泵退化指標趨勢

對特征融合后的退化指標進行歸一化處理后，作為大修閾值模型的輸入數據送入概率神經網絡，構建離心泵運行狀態概率模型，計算概率累計分布函數，并根據式（3）確定其大修閾值。離心泵狀態概率模型及概率累計分布函數如圖4、圖5 所示。

圖4 離心泵狀態概率模型

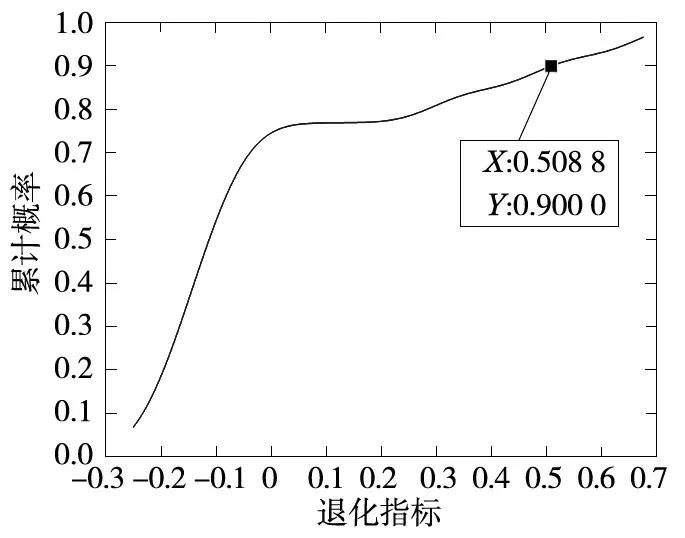
圖5 概率累計分布函數

由圖5 得到累計概率為90%時對應的退化指標值為0.508 8，計算得到大修閾值為0.658 7。已知從第4 組數據開始離心泵狀態出現異常，因此以前4 組數據為基礎，每增加1 組數據重新構建概率模型并計算大修閾值，便可以得到一條動態變化的閾值曲線（圖6）。

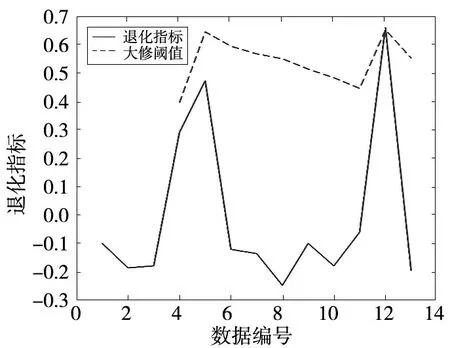
圖6 大修閾值曲線

由表2 可知，編號1～13 數據為某油田作業區離心注水泵2014 年11 月—2016 年7 月監測數據。已知2014 年11 月此臺設備完成大修工作，按作業區《離心注水泵修保規程》中的大修標準及現場設備啟停規律可得下次大修時間應為2016 年7月—2016 年9 月。但由圖7 可得，2016 年5 月離心泵退化指標已超過大修閾值，應進行再次大修。2016 年5 月17 日，現場監測小組監測發現此臺離心泵自由端出現軸承磨損，間隙增大的故障現象，上報站隊進行拆檢維修。拆檢的過程中發現平衡盤折斷、軸套、鎖緊螺母腐蝕磨損等故障，其拆檢情況如圖7、圖8 所示。此時離心泵整體的損壞嚴重程度已達到大修標準。

圖7 平衡盤損壞

圖8 軸套、鎖緊螺母與泵軸抱死

因此，動態大修閾值曲線可以用來反映離心泵真實的運行情況，及時判斷是否進入大修狀態，減少大修前異常停機事故的發生。

4 結論

本文提取離心泵振動指標和特性參數指標組成多源特征集，利用KPCA 特征融合得到表征離心泵整體退化過程的退化指標。通過KPCA 對原始數據進行降維處理，優化PNN 結構；通過GA-PSO 算法優化PNN 平滑因子，提高模型的有效性和容錯能力，基于優化PNN 使用退化指標數據建立離心泵大修閾值模型，進而建立了動態大修閾值曲線。現場大修案例分析表明，利用所建曲線能夠及時判斷離心泵是否應該進行大修，避免大修工作的盲目性，提高生產效率和經濟效益。