Fe-Cr合金晶界偏析及輻照加速晶界偏析的相場模擬*

楊朝曦 柳文波? 張璁雨 賀新福孫正陽 賈麗霞 師田田 惲迪

1) (西安交通大學核科學與技術學院， 西安 710049)

2) (清華大學材料學院， 北京 100084)

3) (中國原子能科學研究院， 北京 102413)

基于WBM相場模型對熱力學條件和輻照條件下Fe-Cr合金晶界處Cr元素偏析行為進行了模擬.模擬結果表明溫度對Fe-Cr合金晶界處Cr元素的偏析有很大影響: 當溫度低于500 ℃時， 晶界處的偏析量很小;而當溫度高于500 ℃時晶界處的偏析量增加明顯.基體中Cr元素含量對晶界Cr元素的相對偏析量也有顯著影響: 隨著基體中Cr元素含量的增加， 相同模擬條件下晶界處Cr元素的相對濃度增量降低.輻照條件下，晶界處Cr元素的相對偏析量比熱力學條件下的相對偏析量有明顯增加; 隨著輻照劑量率的提高， 晶界中心處Cr元素濃度增量變大; 相同輻照條件下， 隨著Cr元素含量的增加， 晶界處Cr元素的相對濃度增量也降低.

1 引 言

鐵素體/馬氏體(F/M)鋼由于具有優于奧氏體鋼的抗輻照腫脹和抗蠕變斷裂等綜合性能， 是一種非常有應用前景的先進核能系統候選材料[1-3]，例如鈉冷快堆的燃料包殼材料、四代堆的壓力容器材料和聚變堆的結構材料等[4].F/M鋼主要是Fe-Cr系的合金， 其中Cr的原子百分比大約為7%—15%.研究表明， 晶界是析出相形核長大的有利位置[5]， 而F/M鋼在晶界處常常會發現Cr元素的輻照誘導偏析(RIS): 晶界處Cr的富集會增加沉淀，從而導致材料的脆化; 而晶界處Cr的耗盡可能會極大地弱化晶界的耐腐蝕性[6].實際上， 在熱力學條件下， Fe-Cr合金中也會發生晶界處Cr元素的偏析， 然而輻照會極大地加速這一過程.Warry和Was[7]的實驗結果表明: Cr的輻照誘導偏析具有溫度依賴性， 在300—600 ℃之間觀察到了Cr的富集， 而在400—500 ℃的輻射溫度下觀察到Cr元素的最大偏析量.因此， 開展熱力學條件和輻照條件下， Fe-Cr合金晶界處Cr元素偏析行為的研究對揭示F/M鋼的服役組織演化和性能退化的機理具有十分重要的科學意義.

數值模擬為研究材料的晶界偏析行為提供了一個重要的工具[8-12].輻照誘導偏析的早期數值模型建立在基于耦合速率方程的基礎上， 該方程依賴于過多的簡化假設， 尤其是在合金化效應處理方面， 忽略了溶劑與局部成分的依賴性[8].Terentyev等[9]利用蒙特卡羅模擬探究了Fe-Cr合金在傾斜晶界處Cr元素的偏析.雖然該模型可以解決上述簡化假設， 但是蒙特卡羅模擬以概率統計理論為基礎， 需要進行大量重復的實驗， 計算量巨大[10]， 而且還要考慮缺陷類型并精確追蹤晶界位置， 從而降低了計算效率.最近， Was等[11]提出原子尺度模型對輻照條件下Cr的偏析行為隨溫度的變化進行研究， 得到了與上述實驗結果相同的溫度依賴性.Xia等[12]利用速率理論對Fe-Cr合金中Cr的輻照誘導偏析進行了模擬， 考慮了缺陷和空洞之間的相互作用并引入了晶界結構的影響， 模擬得到了F/M鋼中RIS的溫度依賴性， 但該方法缺少熱力學基礎.相場模擬方法可以同時考慮動力學與熱力學兩方面因素， 將對元素擴散和再分配的準確描述與較低的計算資源結合起來.

國內外學者利用介觀尺度的相場方法對晶界析出[5，13]和界面偏析行為[14-18]開展了一些研究工作.相場法是基于20世紀50年代的Ginzburg-Landau理論發展而來的， 其思想是在非均勻性體系中引入擴散界面和相場變量， 通過相場變量的變化來表征體系中組織的演化.晶界處合金元素偏析的相場模型主要包括Wheeler等[14]提出的WBM模型和Kim等[15]提出的KKS模型.在WBM模型中， 假設兩相在界面處具有相等的濃度， 在給定點處基體相和晶界相的溶質濃度是相同的; 而在KKS模型中， 假設兩相具有不同的濃度， 這些濃度受到相等的擴散勢的約束， 晶界處的溶質濃度由相濃度之間的混合規則給出.但自由能密度在兩種方法中均由局部相自由能密度之間的混合規則給出[16].最近， Badillo等[17]提出了一維的描述輻照誘導偏析的相場模型.然而該模型不涉及具體的材料熱力學參數， 并且缺少實驗結果的驗證.Piochaud等[18]利用蒙特卡羅模擬計算出相場模型所需參數，使相場模型參數精確化， 并將結果與動力學蒙特卡羅模擬結果進行對比， 在Cr富集對應的溫度范圍內得到了較好的一致性， 但缺少實驗結果的驗證.因此， 關于Fe-Cr合金中Cr元素輻照誘導偏析行為的研究與預測的相場模型目前并不成熟.

本文基于相場模型(WBM模型)， 分析了熱力學條件下不同組成的Fe-Cr合金晶界Cr元素偏析的影響因素.然后， 通過引入輻照加速擴散模型對熱力學條件下的晶界偏析相場模型進行了修正， 進一步研究了Cr元素含量、輻照劑量率和溫度對晶界處Cr元素偏析程度的影響.

2 相場模型

2.1 相場變量

圖1所示為相場變量及其取值的示意圖， 引入了兩個相場變量φ和x來建立相場模型.取向場變量φ用來區分Fe-Cr合金中不同取向的晶粒， 而濃度場變量x表示Cr元素在整個模擬系統中的分布.其中，φ為非保守型相場變量，x為保守型相場變量.φ在晶粒α內的取值為0， 在晶粒β內的取值為1， 而在晶界處，φ的取值從0連續變為1.x的取值由Cr的含量決定， 初始設置為在整個模擬系統中均勻分布.

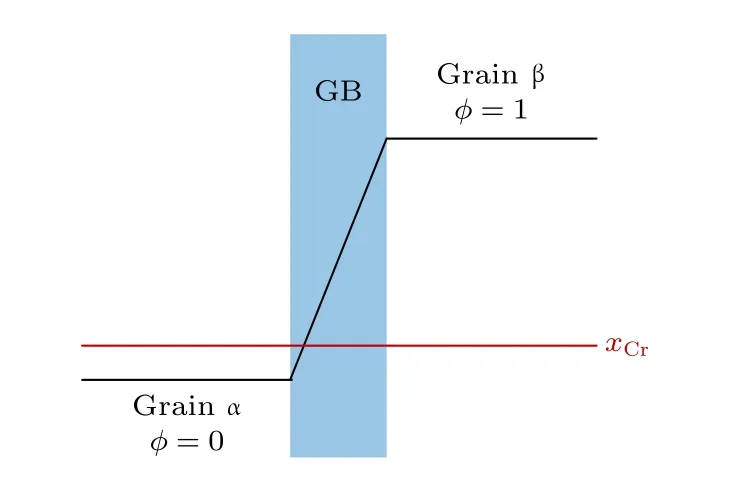
圖1 相場變量φ和x的初始分布Fig.1.Initial distribution of phase field variable φ and x.

2.2 自由能密度函數的構造

Fe-Cr合金體系的總自由能表達式為[19]

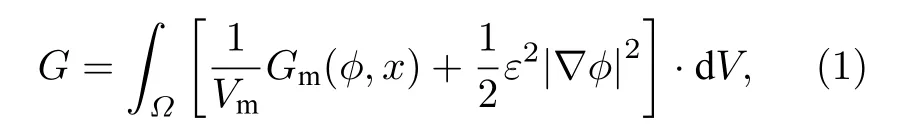
式中，Gm是摩爾吉布斯自由能，x是溶質Cr原子的摩爾分數，Vm是系統的摩爾體積，ε2是能量梯度系數，φ是相場變量.

采用的摩爾吉布斯自由能的表達式為[19]

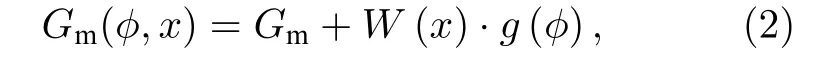
式中，g(φ)=φ2(1-φ)2為在晶界區域引入的雙阱勢函數，W(x)為該雙阱勢函數的高度.根據Gr?nhagen和?gren[19]對晶界偏析的假設， 在W(x)中引入了線性濃度依賴性， 表達式為W(x)=w(1-mx)[20]， 其中w和m均為正數， 系數m描述了溶質與界面之間的相互作用， 可以通過溶質與界面之間的相互作用得出[20].

每個晶粒的摩爾吉布斯自由能表達式利用正則溶體模型表示為[20]

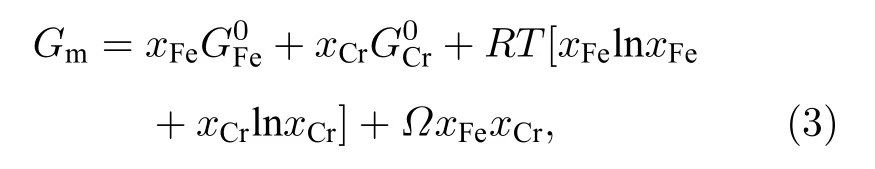
式中，和為標準狀態下純鐵與純鉻的摩爾吉布斯自由能，xFe與xCr為系統中鐵與鉻的摩爾分數，R為通用氣體常數，T為系統的溫度，ΩxFexCr代表的是混合吉布斯自由能.

2.3 熱力學條件下相場方程的演化

非保守型相場變量φ演化動力學方程為Allen-Cahn方程[21]:

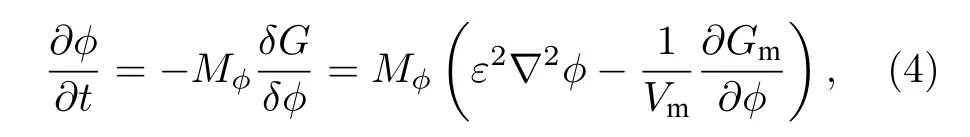
式中，Mφ是與界面遷移率Mint相關的參數， 表達式為

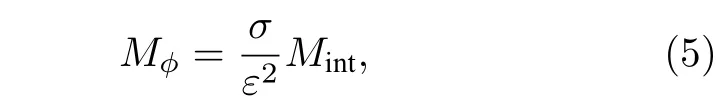
σ為界面能，[20].

保守型變量x的演化動力學方程為Cahn-Hilliard方程[22]:

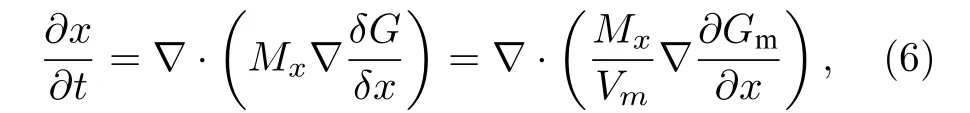
式中，Mx是與擴散系數相關的參數，Mx=x(1-x)VmM， 擴散系數與M之間的關系為D=MRT.

基于快速傅里葉譜方法(FFT)， 通過編寫Matlab程序， 對方程(4)和方程(6)進行聯立求解， 得到了相場變量隨時間的演化過程， 研究熱力學條件下Fe-Cr合金晶界Cr元素偏析行為.模型中采用了周期性邊界條件.

2.4 輻照條件下的模型參數

輻照會在材料中產生大量的空位， 而空位會極大地加速擴散過程， 提高擴散系數.本工作中， 輻照條件下Fe-Cr合金中空位的濃度以及擴散系數的計算參考了Odette等[23]開發的輻照加速擴散模型.輻照條件下的原子擴散系數表達式修正為[24]

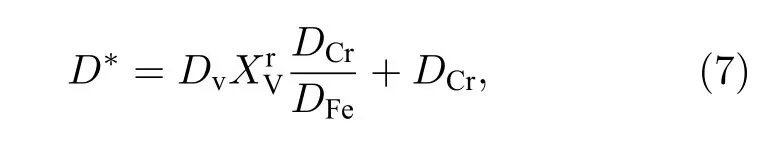
式中，DCr為溶質原子Cr的自擴散系數，DFe為溶劑原子Fe的自擴散系數，DCr和DFe都可以從DICTRA數據庫中獲得[25].為在輻照條件下系統的非平衡空位濃度.

輻照條件下非平衡空位濃度的表達式為[26]

式中，φdpa代表的是輻照劑量率，Dv代表的是空位擴散系數， 可近似表示為Dv=10-4exp[-Em/(kT)] ，Em代表空位的遷移能量[24]，St代表總的沉淀強度，包括位錯(Sd)和空位簇(Sc)的貢獻.Sd通過位錯密度進行表征，Sc的表達式為Sc=4πrcφdpaτc/Va[23]，式中，rc為空位簇的重組半徑，τc為空位簇產生的退火時間，Va為原子體積.空位簇的空間飽和度可能在高輻照劑量率下發生[27]， 因此高輻照條件下，Sc可用空位簇的飽和吸收強度(Ssat)為3 × 1015.gs為空缺產生率， 可由RED模型中的兩個速率方程在穩態條件下求解得到， 表達式為[23]

式中，Di代表間隙原子的擴散系數，Xt代表系統中Cr的原子濃度，Rr代表基體的復合半徑，Rt代表的是陷阱的復合半徑，ξ為級聯效率.τt為捕獲空 位 的 退 火 時 間， 表 達 式 為τt=d2/Dve[-Hb/(kT)]，Hb為捕獲空位的結合能，d為體心立方結構(BCC)的Fe-Cr晶格中的最近鄰距離，k為玻爾茲曼常數.

將(9)式中得到的空缺產生率gs以及不同的輻照劑量率代入(8)式求得輻照條件下的非平衡空位濃度再代入(7)式中得到輻照條件下的原子擴散系數替代熱力學條件下相場模型中Cr原子的自擴散系數.將方程(4)和方程(6)進行聯立求解， 得到輻照條件下相場變量隨時間的演化， 獲得輻照條件下Fe-Cr合金中晶界處Cr元素的偏析行為.

2.5 模擬參數的確定

本文利用相場模型對熱力學條件下和輻照條件下的Fe-Cr合金的晶界偏析情況進行數值模擬，模擬當中用到的Fe-Cr合金的物理參數如表1所列.Fe-Cr合金相場模型中的吉布斯能量表達式中的溶質元素Cr和溶劑元素Fe在標態下的摩爾吉布斯自由能、混合摩爾吉布斯自由能系數以及溶質元素Cr的自擴散系數可從Thermo-Calc數據庫中獲得.

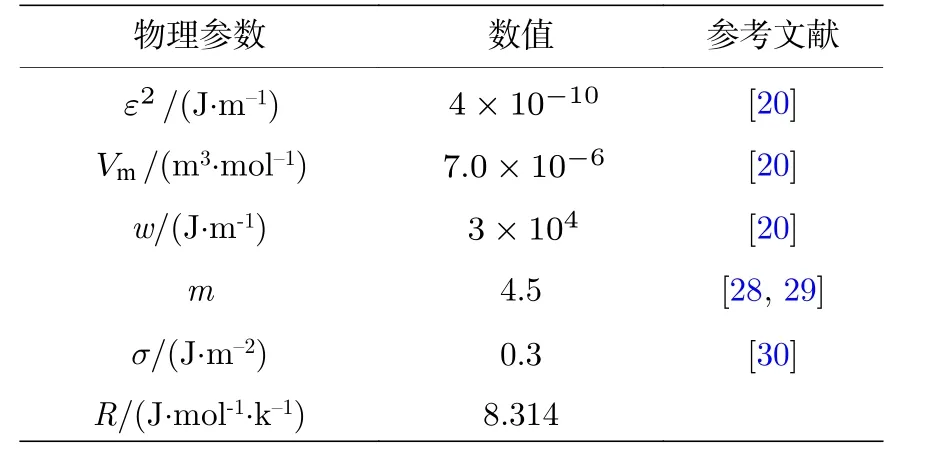
表1 Fe-Cr合金的物理參數Table 1.Physical parameters of Fe-Cr alloys.

為了進一步研究輻照條件下Fe-Cr合金的晶界偏析規律， 應用Odette等[23]開發的輻射增強擴散模型對輻照條件下的原子擴散系數進行修正.需要的參數如表2所列.

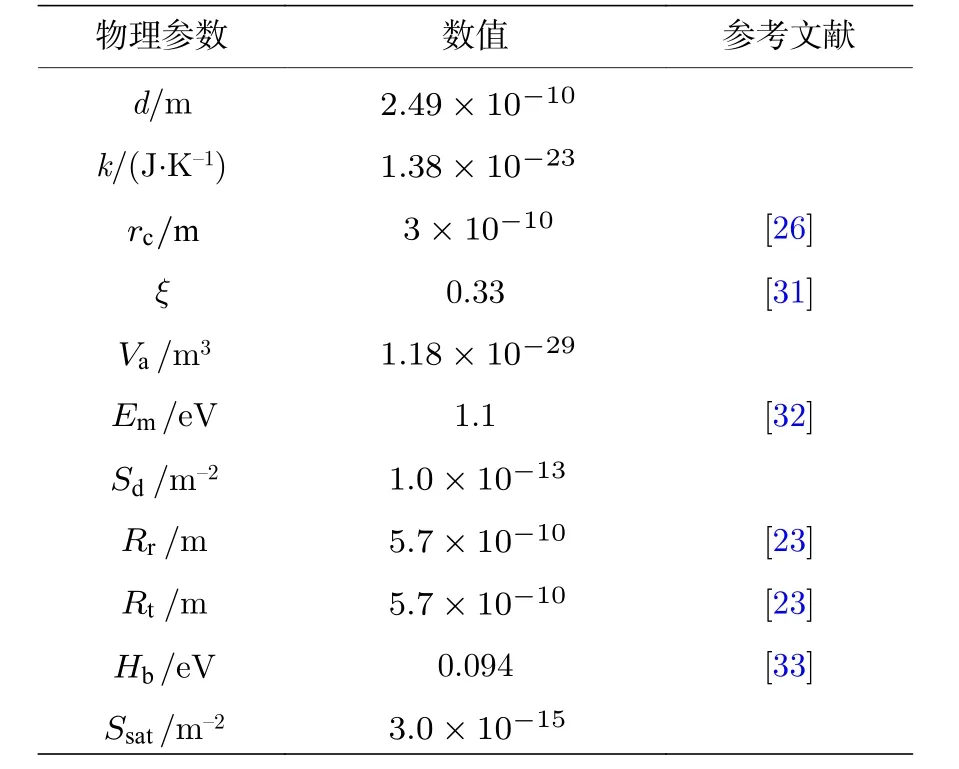
表2 Fe-Cr合金輻照加速擴散模型的參數Table 2.Parameters of radiation enhanced diffusion model of Fe-Cr alloys.

為了便于計算機進行數值模擬， 需要對相場方程中的變量和常數進行無量綱化處理.長度單位的無量綱處理為; 本文選取的標準長度為h=2×10-10m.模擬中選取實際時間間隔為Δt=0.0001s ， 模擬時間的無量綱處理為其中D=MRT被選作參考擴散率.同時， 控制方程中的參數也以無量綱的形式得出MRT/D.

Fe-Cr合金晶界偏析的實驗結果[7]表明， 晶界Cr元素的偏析通常發生于原奧氏體晶界處， 而且原奧氏體晶界寬度為20 nm左右.由于相場方程中的梯度項系數的取值與晶界寬度密切相關[34]，本文通過選取合適的梯度項系數， 將界面寬度也設置為20 nm (對應100個空間離散格點); 整個模擬區域為420 nm (對應2100個空間離散格點).

3 結果與討論

3.1 熱力學條件下的晶界偏析

利用相場模型， 對Fe-Cr合金的熱力學條件下的偏析進行了一維模擬， 分別研究了不同組成的Fe-Cr合金的濃度分布曲線以及溫度對Fe-Cr合金熱力學條件下的偏析的影響.

3.1.1 不同Fe-Cr合金中晶界Cr元素的偏析

圖2分別為Fe-9Cr (含Cr 9%)， Fe-10Cr (含Cr 10%)， Fe-12Cr (含Cr 12%)， Fe-15Cr (含Cr 15%)四種合金在500 ℃溫度下晶界附近的濃度分布圖(濃度用質量分數表示).本文中所有濃度場分布圖的橫坐標代表距離晶界中心的距離， 橫坐標為0時代表晶界的中心; 縱坐標代表Fe-Cr合金中溶質元素Cr的濃度.圖2中五種顏色的曲線分別代表時間為20—100 s的濃度分布曲線.可以看出，濃度分布圖以晶界中心呈現兩邊對稱.在演變過程中， 晶界的位置不隨時間的進行而發生變化， 這是由于本文選用的是平直界面， 沒有晶界移動的驅動力[35].在晶粒α和晶粒β中， Fe-Cr合金中Cr元素的濃度保持在初始狀態不變; 而在晶界處， Cr隨著時間的增加向晶界處發生富集， 在晶界中心處達到最大偏析量.隨著時間的進行， 溶質元素Cr的最大偏析量也隨之增加.

圖3(a)為500 ℃時不同組成的Fe-Cr合金在相同時間之后晶界附近的濃度分布圖.可以看出，隨著Cr含量的增加， 濃度演變曲線的峰值也隨之增加， 即晶界中心處的最大偏析量隨之增大， 這與賈麗霞等[36]得到的模擬結果一致.圖3(b)為500 ℃時不同組成的Fe-Cr合金在相同時間之后變量φ的演變曲線，φ的值從0變化到1的區間即為晶界區域.可以看出， 隨著Cr含量的增多晶界的位置沒有發生變化， 但晶界的寬度隨著Cr濃度的增加而增加， 合金Fe-15Cr的晶界寬度最大， 說明溶質元素的濃度是影響晶界寬度的因素.

圖4為500 ℃時不同組成的Fe-Cr合金在100 s之后晶界中心處的相對Cr濃度增量和初始Cr濃度的關系曲線.相對Cr濃度增量的計算由公式 ΔCrelative=(c-c0)/c0得 到， 其 中c0代 表 初 始Cr濃度，c代表100 s時晶界中心處的最大偏析量.可以看出， 隨著Cr含量的增加， 晶界中心處相對Cr濃度增量在降低， 并且呈現線性降低的關系.

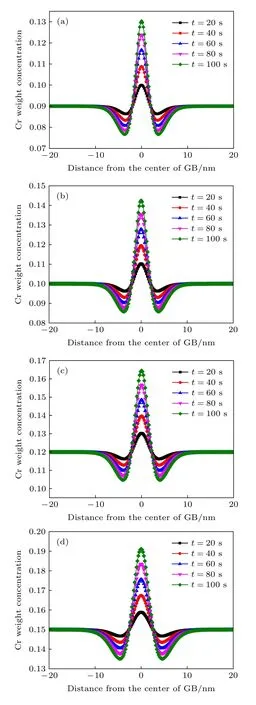
圖2 Fe-Cr合金中晶界處Cr元素濃度的變化曲線 (a) Fe-9Cr; (b) Fe-10Cr; (c) Fe-12Cr; (d) Fe-15CrFig.2.Evolution of Cr concentration at grain boundary in Fe-Cr alloys: (a) Fe-9Cr; (b) Fe-10Cr; (c) Fe-12Cr; (d) Fe-15Cr.

圖3 500 ℃模擬100 s后不同成分的Fe-Cr合金的相場變量 (a) x; (b) φFig.3.The curves of the phase field variables of Fe-Cr alloys with different compositions after 100 s at 500 ℃: (a) x;(b) φ.

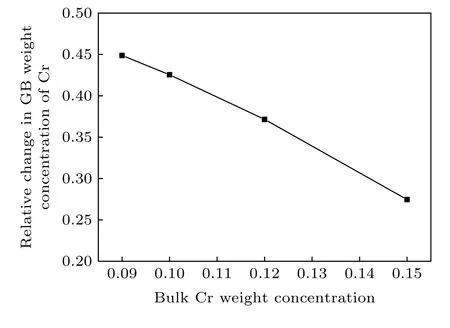
圖4 500 ℃下100 s后晶界處的相對Cr濃度增量和基體中Cr濃度的關系曲線Fig.4.The relationship between the relative change of Cr concentration at grain boundary and the bulk Cr concentration after 100 s at 500 ℃.

3.1.2 溫度對晶界Cr元素偏析的影響

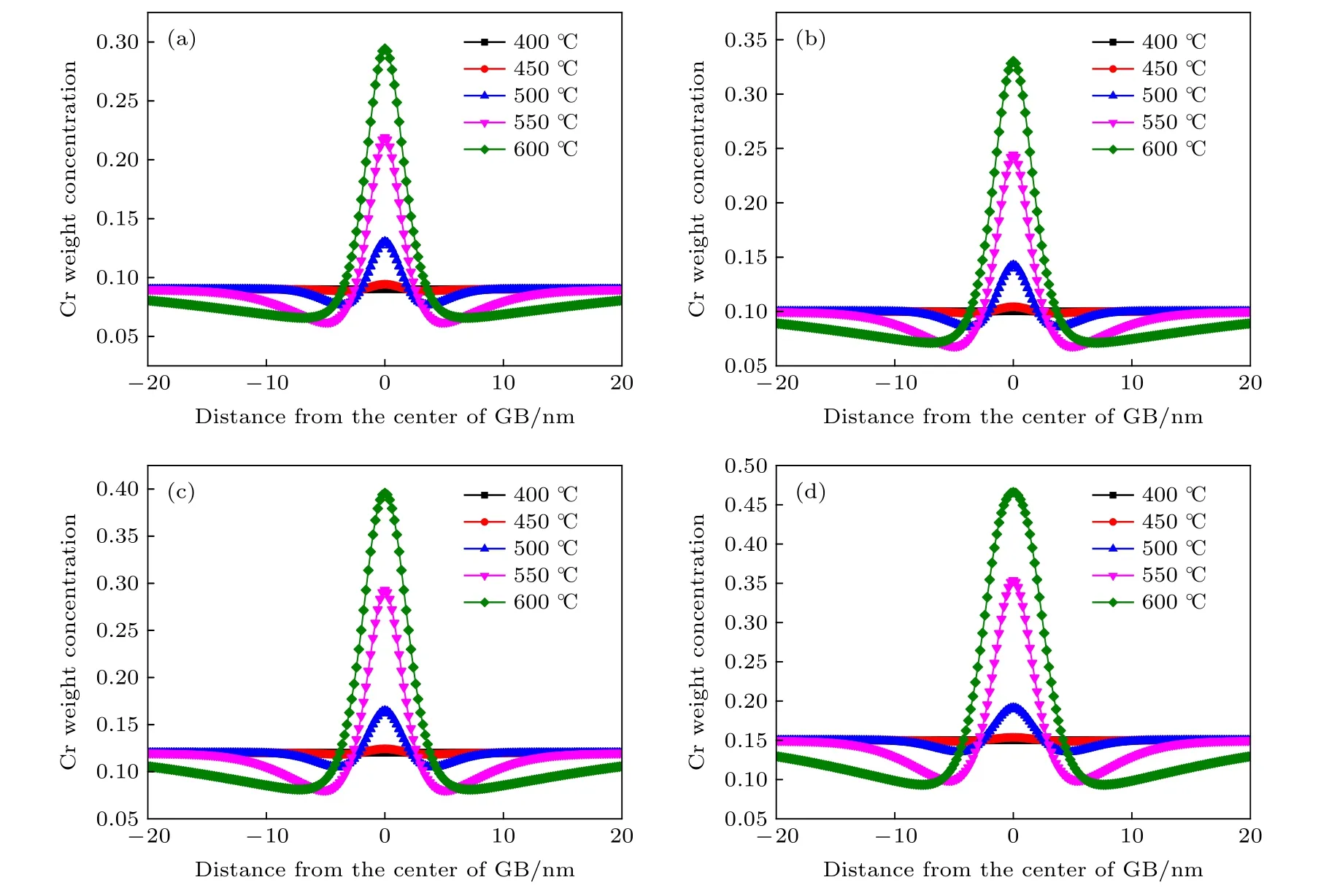
圖5 不同溫度下晶界處Cr元素的濃度分布 (a) Fe-9Cr; (b) Fe-10Cr; (c) Fe-12Cr; (d) Fe-15CrFig.5.Distribution of Cr concentration at grain boundary with different temperatures: (a) Fe-9Cr; (b) Fe-10Cr; (c) Fe-12Cr;(d) Fe-15Cr.

圖5 中的4個圖分別為Fe-9Cr， Fe-10Cr， Fe-12Cr， Fe-15Cr等4種合金在400， 450， 500， 550，600 ℃下100 s時晶界附近的濃度分布圖.圖中5種顏色的曲線代表相同時刻不同溫度下的濃度分布曲線.可以看出， Fe-Cr合金在不同溫度下濃度演變曲線的趨勢相同， 在晶粒α和晶粒β中， Fe-Cr合金中Cr元素的濃度保持在初始狀態不變; 在晶界處， Cr向晶界處發生富集， 在晶界中心處達到最大偏析量.在相同的時間條件下， 最大偏析量隨著溫度的升高而升高.當溫度低于500 ℃時， 晶界處的偏析量很小， 晶界偏析不明顯; 當溫度高于500 ℃時晶界處的偏析量突然增多.McLean理論[37]指出， 當系統保溫很長一段時間之后系統所達到熱力學平衡狀態下的偏析量會隨著溫度的升高而降低，與本文得到的模擬結果相反.這可能是由于本工作中時間較短且未達到平衡所需要的時間， 所以晶界處的最大偏析量隨擴散系數的變化而變化， 溫度升高， 擴散系數增大， 晶界處的最大偏析量也相應升高.這與Sean[38]利用McLean理論[37]分析得出的短時間內的晶界偏析動力學基本一致.

3.2 輻照條件下的晶界偏析行為

3.2.1 不同Fe-Cr合金中晶界Cr元素的偏析

將輻照加速擴散模型引入相場模型， 即對擴散系數進行修正.對加入輻照之后的Fe-Cr合金的晶界偏析進行了一維模擬.圖6為在450 ℃下輻照劑 量 率 為10—4dpa/s時Fe-9Cr， Fe-10Cr， Fe-12Cr， Fe-15Cr等4種合金晶界附近的濃度分布圖.圖中5種不同顏色的曲線代表時間為20—100 s的濃度演變曲線.可以發現， 隨著時間的進行， Cr向晶界處發生富集， 在晶界中心處達到最大偏析量.

圖7為450 ℃溫度下輻照劑量率為10—5dpa/s時Fe-9Cr， Fe-10Cr， Fe-12Cr， Fe-15Cr四種合金的晶界附近的濃度分布圖.圖中5種不同顏色的曲線代表20—100 s之后的濃度分布圖， 隨著時間的進行， Cr元素在晶界處發生富集， 在晶界中心處達到偏析最大量.

3.2.2 輻照劑量率對晶界Cr元素偏析的影響

圖8為Fe-9Cr， Fe-10Cr， Fe-12Cr， Fe-15Cr等4種合金在450 ℃下無輻照以及輻照劑量率為10-4，4×10-5和 1 0-5dpa/s 時演變100 s之后晶界附近Cr濃度分布對比圖.可以看出， 同一種合金在相同的溫度和時間下隨著輻照強度的增加，Cr原子在晶界處的偏析越來越明顯， 對應的濃度峰值也越來越大， 實現了輻照對晶界處原子擴散的增強.該結果與Warry和Was[7]研究的模型合金在晶界附近Cr濃度分布隨輻照強度的變化趨勢基本一致.

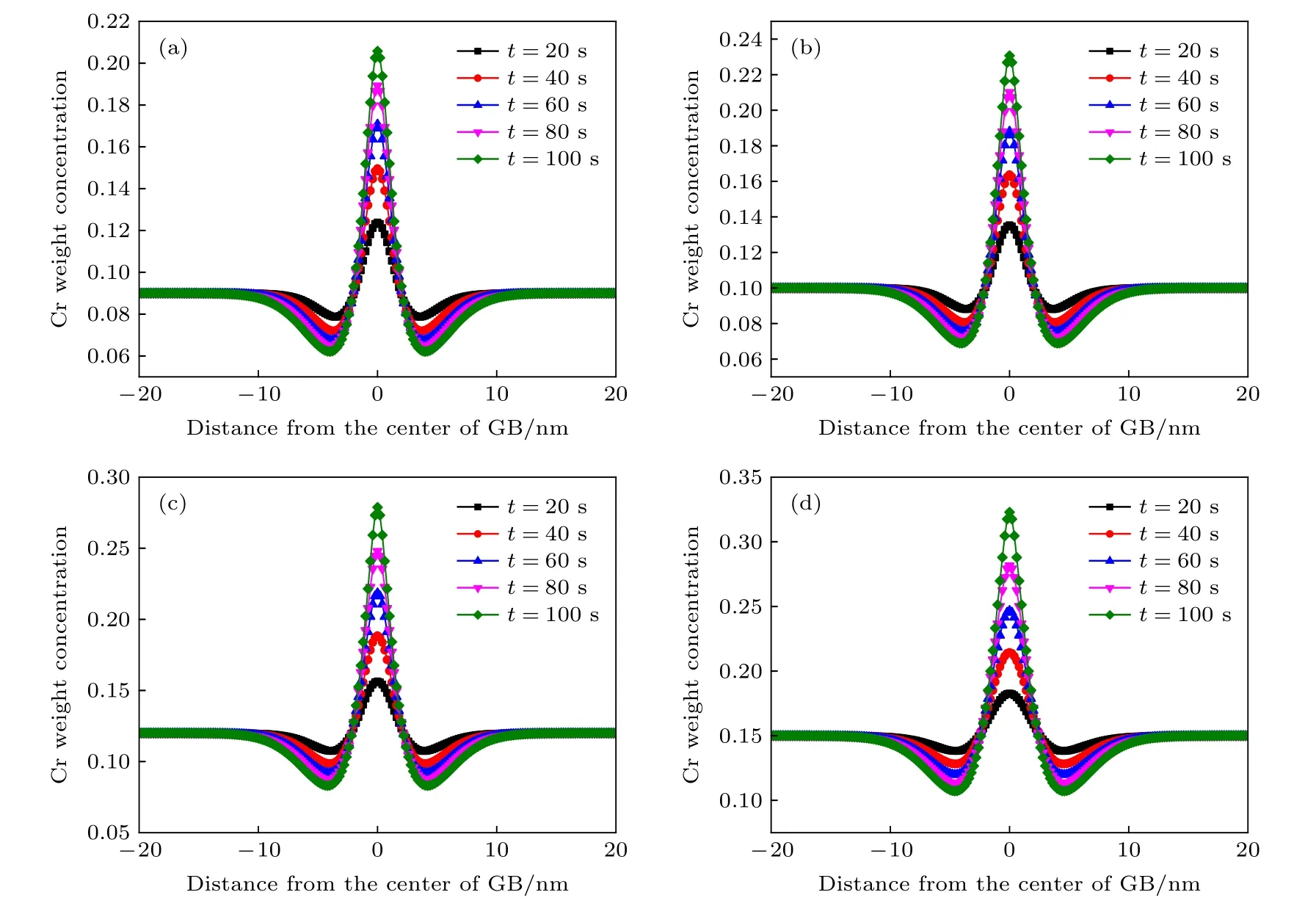
圖6 450 ℃輻照劑量率為10—4 dpa/s下晶界處Cr元素的濃度分布 (a) Fe-9Cr; (b) Fe-10Cr; (c) Fe-12Cr; (d) Fe-15CrFig.6.Concentration distribution of Cr element at GB at a dose rate of 10—4 dpa/s at 450 ℃: (a) Fe-9Cr; (b) Fe-10Cr; (c) Fe-12Cr;(d) Fe-15Cr.

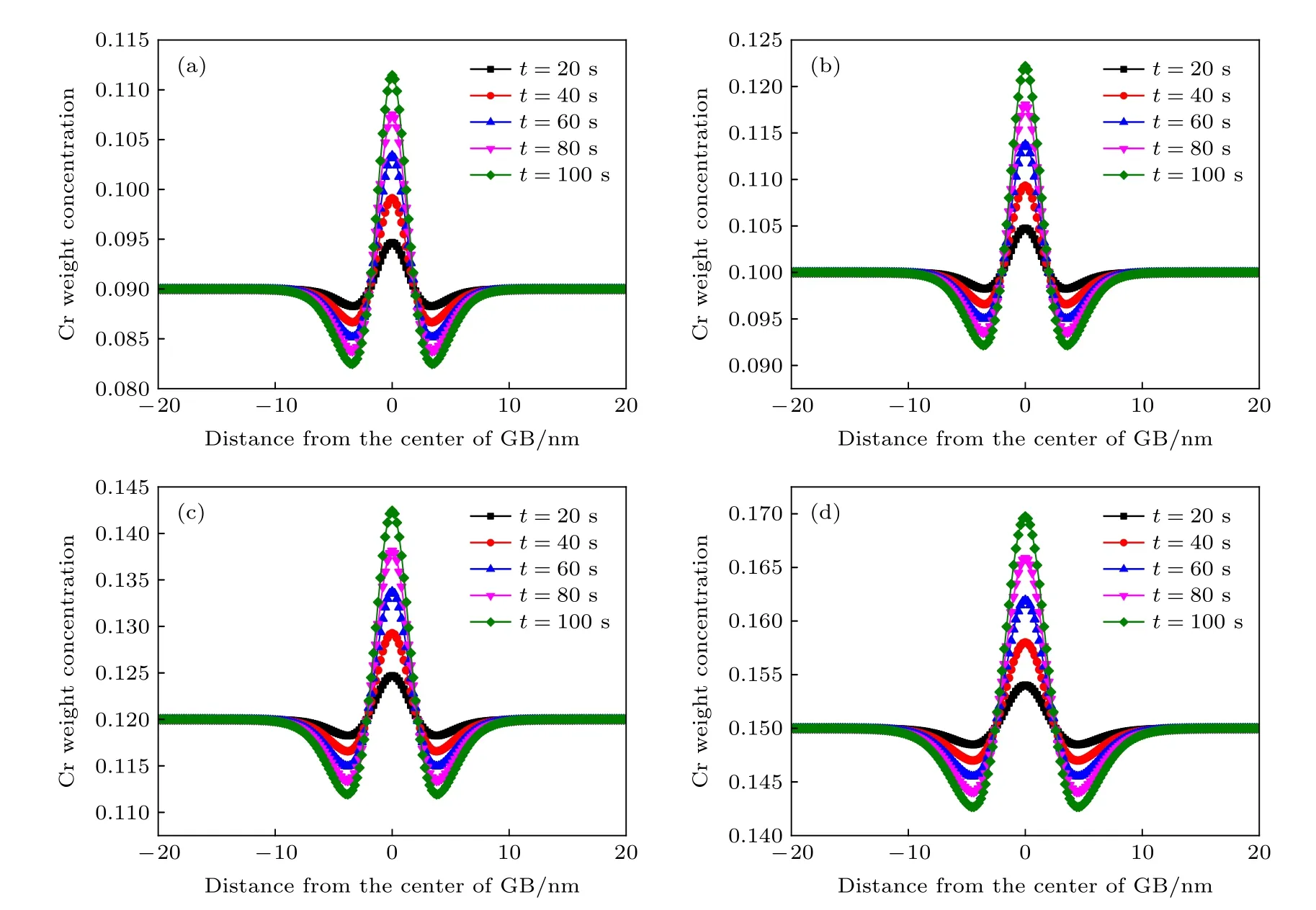
圖7 450 ℃輻照劑量率為10—5 dpa/s下晶界處Cr元素濃度的變化曲線 (a) Fe-9Cr; (b) Fe-10Cr; (c) Fe-12Cr; (d) Fe-15CrFig.7.Evolution of Cr concentration at grain boundary with a dose rate of 10—5 dpa/s at 450 ℃: (a) Fe-9Cr; (b) Fe-10Cr; (c) Fe-12Cr; (d) Fe-15Cr.

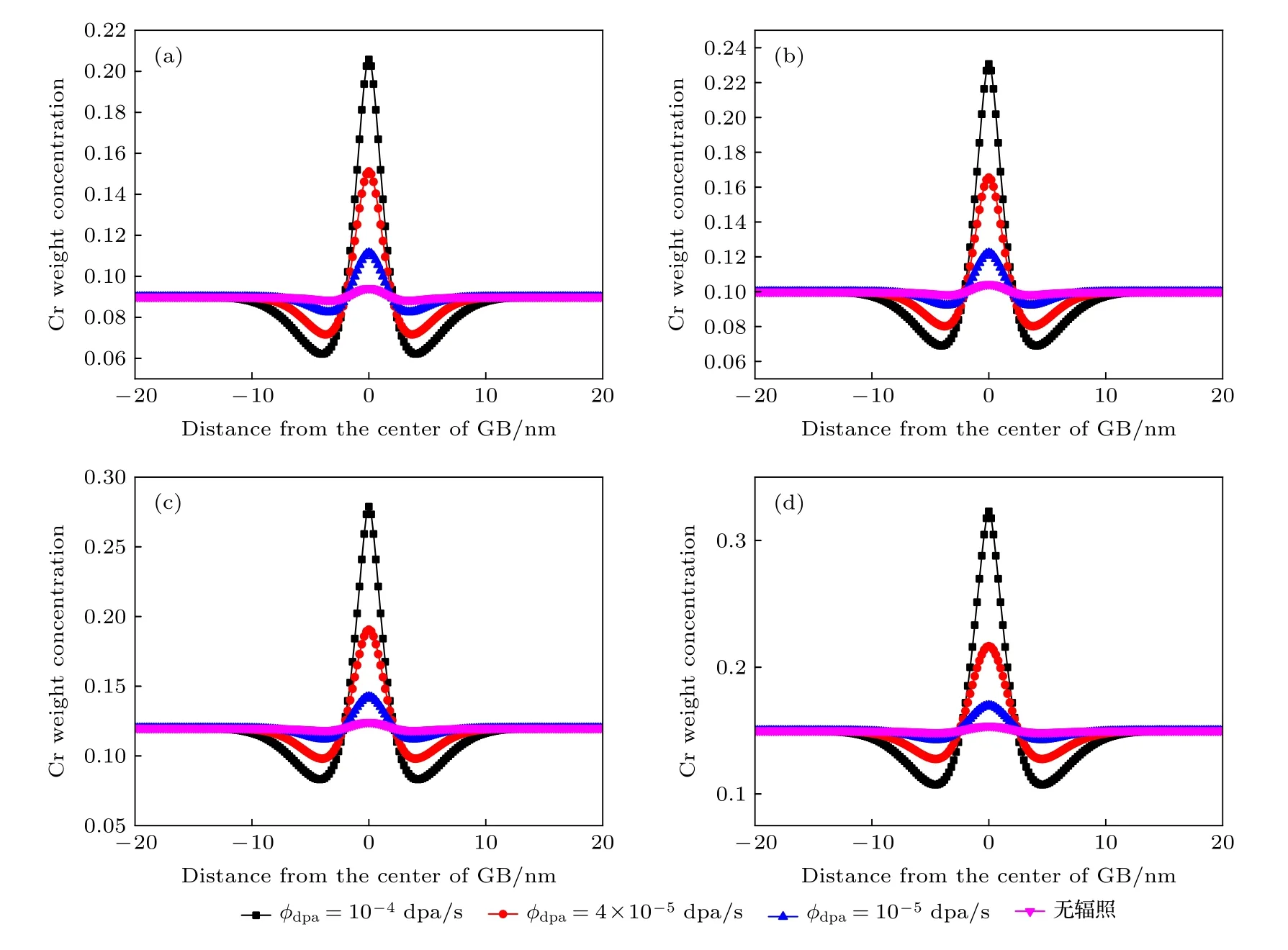
圖8 不同輻照劑量率下晶界處Cr元素濃度的分布 (a) Fe-9Cr; (b) Fe-10Cr; (c) Fe-12Cr; (d) Fe-15CrFig.8.Distribution of Cr concentration with different dose rates: (a) Fe-9Cr; (b) Fe-10Cr; (c) Fe-12Cr; (d) Fe-15Cr.

圖9 為Fe-9Cr合金在450 ℃不同劑量率條件下晶界處的相對Cr濃度增量和初始Cr濃度的關系曲線.可以看出， 隨著劑量率的升高， 晶界中心處相對Cr濃度增量升高.輻照劑量率為4×10-5，10-5dpa/s 時， 同無輻照時隨濃度變化趨勢相同， 隨著濃度的升高相對濃度增量降低， 合金Fe-9Cr的Cr濃度相對增量最多.但在輻照劑量率為 1 0-4dpa/s 時， 晶界處相對Cr濃度增量隨濃度的升高先升高再降低， Fe-12Cr合金的Cr濃度增量是最多的.Warry和Was[7]的實驗中也得到了隨著Cr濃度的升高， 晶界中心處的相對Cr濃度增量降低.這是由于間隙遷移能對Cr的濃度具有依賴性， 隨著Cr濃度的增加單個自間隙原子的遷移能會降低， 從而影響Cr元素的擴散系數[7].因此， 隨著基體相中Cr濃度的增加， 較低的間隙遷移能會導致更多的Fe間隙原子向晶界擴散， 從而限制Cr在晶界的富集量.

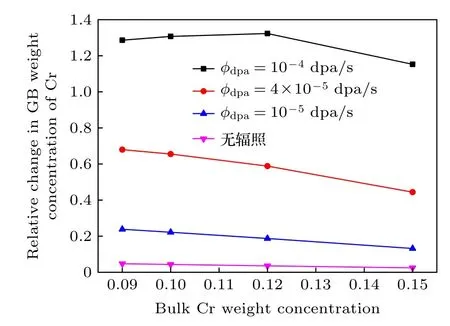
圖9 450 ℃時不同劑量率下晶界處的相對Cr濃度增量和初始Cr濃度的關系曲線Fig.9.The relationship between the relative change of Cr concentration at grain boundary and the bulk Cr concentration at different dose rates at 450 ℃.

圖10 為Fe-8.5 Cr模型合金和實驗下測得的T91鋼在輻照劑量率為1.2 × 10—5dpa/s， 溫度為400 ℃和450 ℃條件下的濃度分布曲線的對比圖.離散的點代表Warry和Was[7]關于T91在輻照條件下晶界偏析的實驗研究結果， 平滑的曲線代表的是本文利用相場方法模擬的Fe-8.5Cr合金的濃度分布曲線; 黑色曲線代表的是400 ℃時的模擬與實驗結果， 紅色曲線代表的是450 ℃時的模擬與實驗結果.本工作相場模擬得到的晶界處的最大偏析量與實驗結果基本一致; 兩個溫度對比可知， 在400—450 ℃時對應的最大偏析量隨溫度的增加而增加， 與實驗所測得的趨勢一致.

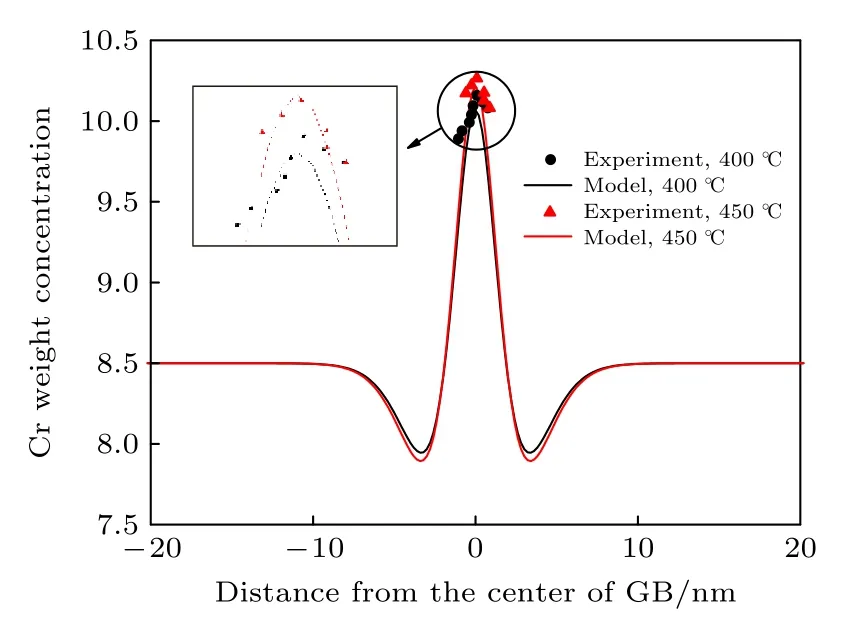
圖10 輻照劑量率為1.2 × 10—5 dpa/s時模擬結果與實驗結果對比Fig.10.Comparison of simulation results and experimental results when the dose rate is 1.2 × 10—5 dpa/s.

4 結 論

溫度對Fe-Cr合金晶界處Cr元素的偏析程度有明顯的影響.這是由于隨著溫度的升高， Cr原子的擴散也快速增加， 導致晶界處Cr元素的偏析程度顯著提高.模擬發現: 當溫度低于500 ℃時， 晶界處的偏析量很小， 晶界偏析不明顯; 當溫度高于500 ℃時晶界處的偏析量增加明顯.

基體中Cr元素含量對晶界Cr元素的相對偏析量也有很大的影響.相同熱力學條件下， 隨著基體中Cr元素含量的增加， 晶界處Cr元素的相對濃度增量降低.

引入輻照條件后， 晶界處Cr元素的相對偏析量比熱力學條件下的偏析量有明顯增加.這是由于輻照產生的大量的點缺陷極大地提高了Cr元素的擴散系數.隨著輻照劑量率的提高， 晶界中心處相對Cr元素濃度增量變大.相同輻照條件下， 隨著Cr元素含量的增加， 晶界處Cr元素的相對濃度增量也降低.