金屬Nb的Finnis-Sinclair勢開發及勢函數形式對材料性能的影響*
高靜怡 孫嘉興 王遜 周剛 王皞 劉艷俠? 徐東生
1) (遼寧大學物理學院, 沈陽 110036)
2) (沈陽建筑大學理學院, 沈陽 110168)
3) (中國科學院金屬研究所, 沈陽 110016)
對于計算材料科學的研究者來說, 經常由于找不到合適的原子間勢而工作受阻.本文將在Finnis-Sinclair勢的框架下, 通過開發金屬Nb的Finnis-Sinclair勢而給出較詳細的原子間勢擬合、檢驗、修正的過程.首先建立原子間勢與材料宏觀性能之間的關系, 然后通過再現金屬Nb的結合能、體模量、表面能、空位形成能及平衡點陣常數的實驗數據的方法擬合金屬Nb的Finnis-Sinclair勢.利用所構建的原子間勢計算金屬Nb的彈性常數、剪切模量及柯西壓力來檢驗勢函數.討論勢函數曲線形狀對間隙形成能的影響, 進而根據間隙能的計算數據修正已構建的原子間勢.討論截斷距離的處理方法.本文的結果一方面為構建原子間勢函數庫提供資料, 為構建與Nb相關的合金原子間勢奠定基礎; 另一方面, 為開發和改善原子間勢質量提供方法和依據.
1 引 言
原子尺度模擬是微觀層次研究材料性能行之有效的手段和途徑, 但是計算機模擬結果的可靠性直接來源于原子間勢的質量[1], 而且模擬的計算量強烈依賴于原子間勢的復雜度.因此開發形式簡單、質量可靠的原子間勢及建立易于操作的原子間勢構建方法極為重要.目前, 原子間勢的開發大多通過有限的勢函數參數來再現材料的部分性質而獲得[2-4], 因此, 根據部分性能獲得的原子間勢不可能描述材料的全部性能.由于研究目的不同, 有時即使是同一金屬[5-10]或合金[11,12]也需要開發不同的原子間勢.
Nb基合金及含Nb合金在航空航天、醫學、核工業等領域有著重要的應用[13-15].為了從原子尺度研究Nb及其合金的性能, 首先需要構建其原子間勢.在金屬及合金中應用廣泛的原子間勢模型主要是1983—1984年間由Daw和Baskes[16,17]提出的Embedded-atom method (EAM)勢模型, 以及1984年由Finnis和 Sinclair[2]提出的Finnis-Sinclair (FS)勢.二者數學表達式都由兩項組成,第一項都為排斥勢, 解釋相同, 都是原子芯之間的靜電勢; 第二項都為吸引勢.二者的主要區別在于第二項, 體現在兩個方面: 一是來源不同, EAM勢來源于密度泛函理論, FS勢來源于緊束縛理論的二階矩近似; 二是對第二項即電荷密度函數和嵌入能函數的解釋不同, EAM勢中, 把金屬中的每個原子看成是鑲嵌在其他原子在該位置形成的電子氣中的一個雜質, 并假設嵌入能是局域電子密度及其高階導數的函數, 且電子密度由原子的電荷密度疊加而成; 而FS勢中, 每個原子內聚能的大小與原子間最近鄰的鍵合數的平方成正比, 在緊束縛理論中, 金屬中電子能帶的帶能是其中占據態單電子能之和, 而且帶能由態密度的二階矩來表征, 因此密度函數是態密度的二階矩.雖然這兩種原子間勢的來源和解釋不同, 但由于二者的數學形式相近,為此, 人們習慣上將FS勢歸入為EAM模型.本文為了敘述上的方便, 仍然稱作FS勢.到目前為止,在金屬及合金中廣泛使用的原子間勢形式依然是EAM勢及FS勢, 以及對這兩種勢的各種修正勢[18-20].
1984年Finnis和 Sinclair[2]開發了7種bcc結構金屬Nb, V, Ta, Cr, Mo, W及Fe的FS勢, 首次考慮了原子之間的多體效應, 克服了對勢的缺點.但該勢的缺點是在近距離下原子之間的排斥力不足, 特別是V和Nb, 在短距離內甚至表現出有吸引力, 導致分子動力學模擬時出現原子落在一起的異常行為[21].為此, Ackland[21]和Rebonato[22]分別對該問題進行了修正, 對于小于第一近鄰的對勢曲線進行了硬化.另一方面, 該勢的原子間相互作用距離考慮到第二近鄰, 相互作用距離比較短.本文在該勢的基礎上, 首先, 擴展相互作用距離到第三近鄰, 并修正近距離相互作用偏軟的現象; 其次, 建立原子間勢與材料宏觀性質之間的關系, 討論函數形式及截斷距離對宏觀性能的影響, 并根據材料的宏觀性質修正原子間勢函數形式.
構建原子間勢是一項復雜的工程, 本文將從模型的選擇, 截斷距離處理, 勢函數擬合, 勢函數檢驗及應用, 以及根據檢驗和應用結果修正勢函數幾方面詳細介紹勢函數的開發過程, 并就截斷距離和勢函數形式對原子間勢的質量及材料性能影響方面進行了討論, 期望為開發和改善原子間勢質量提供參考.
2 模 型
本文在FS勢框架下[2]開發金屬Nb的原子間勢, 將原子間相互作用擴展到第三近鄰.對于理想單質金屬, 所有原子都是等價的, 因此體系的總能可以表示為單原子能量之和, 單個原子的相互作用能表示為:

其中,uP表示原子對之間的相互作用能,uN表示多體相互作用對總能的貢獻.它們可用(2)式和(3)式表示:

其中,A為勢參數, 是大于零的常數.根據緊束縛理論, 取ρ為參考原子i處的局域電子密度, 表示如下:

其中,φ(ri)為重疊積分的平方和[2]或為原子電荷密度[17].
原始模型中的φ(ri) 為拋物線型函數, 當將截斷距離擴展到第三近鄰時, 使用原函數形式給出了不合理的原子間相互作用, 為此本文修正該函數為四次冪形式:

原始模型中的對勢函數V(r)為四次多項式, 本文修正為六次多項式:
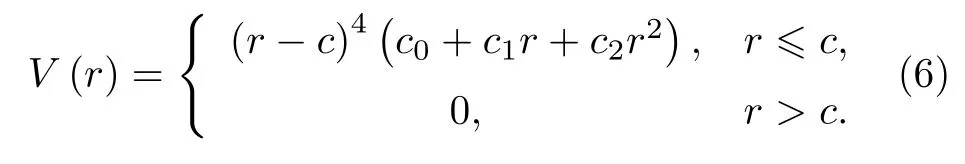
函數形式的選擇和c與d的取值在后面詳細討論.c與d是截斷參數, 選取在第三近鄰與第四近鄰之間,c和d的值分為:

其中,a為Nb的晶格常數.
3 截斷處理方法
為了減少分子動力學模擬計算原子受力所用時間, 通常不采用相互作用減少到零的自然截斷的方式, 而是在一個方便的力程上將原子間相互作用截斷.有研究表明, 如果預先不做截斷處理, 計算一個分子動力學步的99%的時間都將用于計算使粒子運動所需的力.
如果勢能不是光滑截斷, 那么在截斷點上的力就會出現δ函數形式的奇異性, 因此, 必須考慮勢能的截斷對系統特性的影響.首先需要保證勢能及其一階、二階導數在截斷點連續.勢能對距離的一階導數對力有影響, 勢能對距離的二階導數對材料的彈性常數、體模量、剪切模量等有影響.這些函數是否連續、力程的大小對材料的結構穩定性、力學穩定性、相變等都有影響.
可以采取多種方法對勢函數進行截斷, 如:1)簡單地將函數平移; 2)將函數在適當位置截斷,再增加截尾函數; 3)在適當位置迭加一個截尾函數; 4) 將截斷函數直接包含到勢函數表達式中.
其中方法1)比較粗糙, 且不能保證勢函數的一、二階導數連續, 只適合做靜態的與能量相關的計算.方法2)和方法3)需要增加參數的數量, 以保證在函數連接點的各階導數連續, 且要慎重考慮連接點的選取.方法4)是目前使用比較多的方法,優點是與勢函數同時進行參數擬合.目前常用的主要有兩種形式, 一是Finnis和Sinclair使用的階躍函數的形式

即在選取的勢函數上直接乘以H(x); 另一種是Mishin[23]使用的截斷方式,

也是在勢函數上直接乘以ψ(x).
4 原子間勢與晶體性質
不論是擬合原子間勢還是檢驗原子間勢, 均需建立原子間勢與擬合晶體性質參數及檢驗晶體性質參數之間的關系.本文建立了內聚能、平衡點陣常數、體模量、表面能、空位形成能、間隙能及切變模量之間的關系.
對于體心立方晶體, 設晶格常數為a, 平衡態下的原子體積,Ωe=a3/2.本文構建的原子間勢的相互作用在原子的第三和第四近鄰之間截斷.bcc晶體第一近鄰有8個原子,距離為第二近鄰有6個原子, 距離為a; 第三近鄰有12個原子,距離為
采用(10)式的符號來標記不同近鄰下的對相互作用及電子密度,

4.1 壓力和體模量

其中,PN和PP分別表示為N體相互作用和兩體相互作用部分的力.由

得
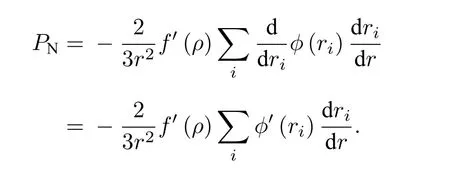
當r=a時, 可得到平衡狀態下的壓力:


由

得

當r=a時, 可得到平衡狀態下的體模量:

4.2 表面能
表面能Esurf的計算公式為:

其中,Es為具有表面時體系的總能,Et為不包含表面時體系的總能,S為計算體系表面的面積.考慮(100)面截斷距離內原子能量的變化, (100)面的表面能為:
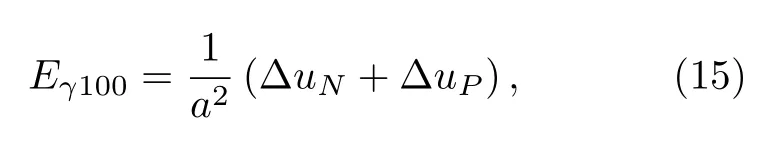
其中,

4.3 未弛豫空位形成能
單空位形成能為:
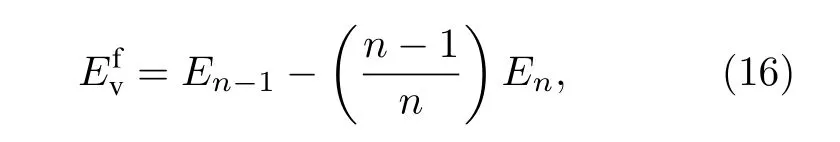
其中,En—1為具有n個原子的晶體在其內部產生一個空位時體系的總能,En為具有n個原子的理想晶體體系的總能.考慮空位周圍截斷距離內原子能量的變化, 即為單空位形成能.

4.4 內聚能
在FS勢下, 每個原子的內聚能為:

4.5 平衡條件
平衡狀態下, 晶體內各原子受力為零, 總能量最低, 即utot關于r的一階導數為0.因此, 當r=a時的平衡條件為:

其中,

4.6 自間隙形成能
自間隙形成能的計算公式為:
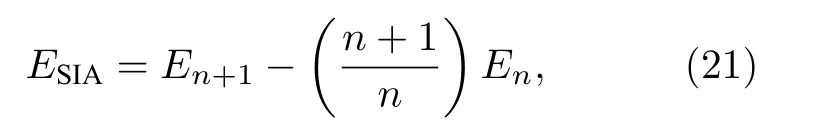
其中,En表示具有n個粒子的理想晶體的總能量,En+1表示存在一個間隙原子時體系的總能量.本文考慮圖1所示的6種間隙構型.
本文采用計算缺陷范圍內的原子間相互作用能量變化的方法計算每種間隙的形成能.八面體、四面體及擠列子3種間隙構型中, 在截斷距離內的每個原子除了距離的原子有8個, 距離為a的原子有6個, 距離為的原子有12個外, 還增加了一個間隙原子的相互作用, 截斷距離內的這些原子與間隙原子的距離及等價原子數見表1.啞鈴構型中, 截斷距離內的原子分布要復雜一些, 可通過Materials Studio軟件建立相應的構型, 再分析近鄰原子分布情況.
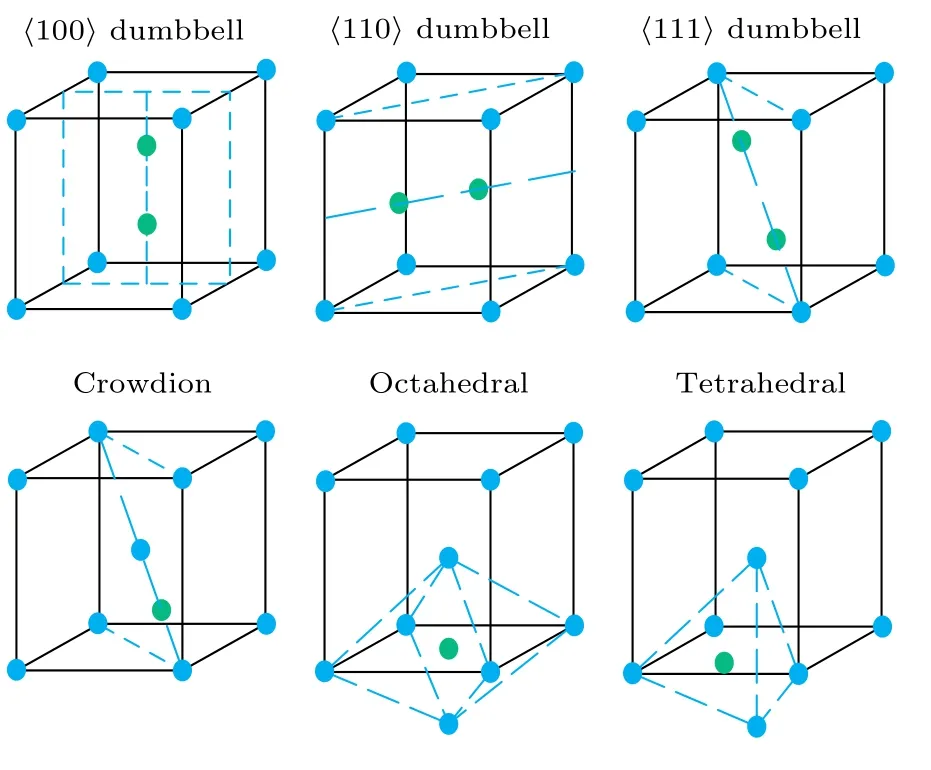
圖1 bcc結構6種間隙構型Fig.1.Six interstitial configurations of bcc structure.
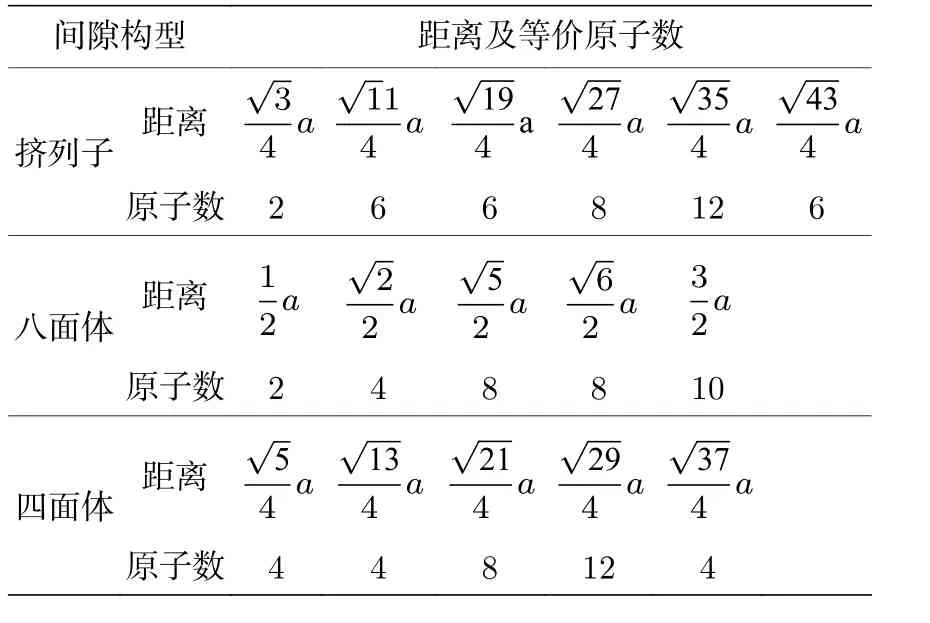
表1 截斷距離內的各間隙原子的距離及等價原子數Table 1.Distance and equivalent atomic number of each atom withinthe cutoff distance from the interstitial atom.
根據間隙原子的近鄰分布可計算間隙原子的形成能.
八面體間隙形成能為:

其余構型的間隙形成能可采用同樣方法計算.

4.7 立方晶體的切變模量C44和C'
我們知道, 應變能密度為
其中,σij=Cijklεij.
按照Voigt記法, 可得應變能密度為

立方晶體有兩個切變模量C44和C′(≡(C11—C12)/2).
對于C′, 考慮立方晶體的平面應變,X方向伸長時應變為ε11,Y方向縮短時應變為ε22,Z方向不變時應變為0.保持體積不變, 則ε11= —ε22.對于C44, 相當于在[011]方向的拉伸, 只有應變為ε12, 將應變分量代入(24)式, 得到兩種應變下的應變能密度分別為
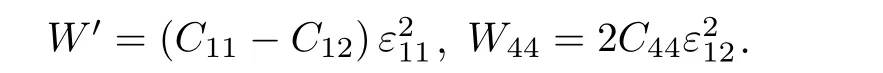
可得

應變能密度W為單位體積的內能, 則
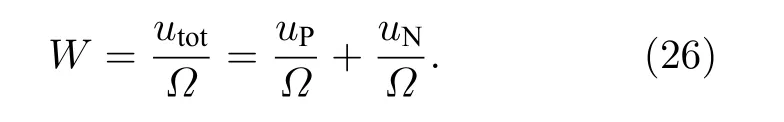
經推導(見附錄A)得
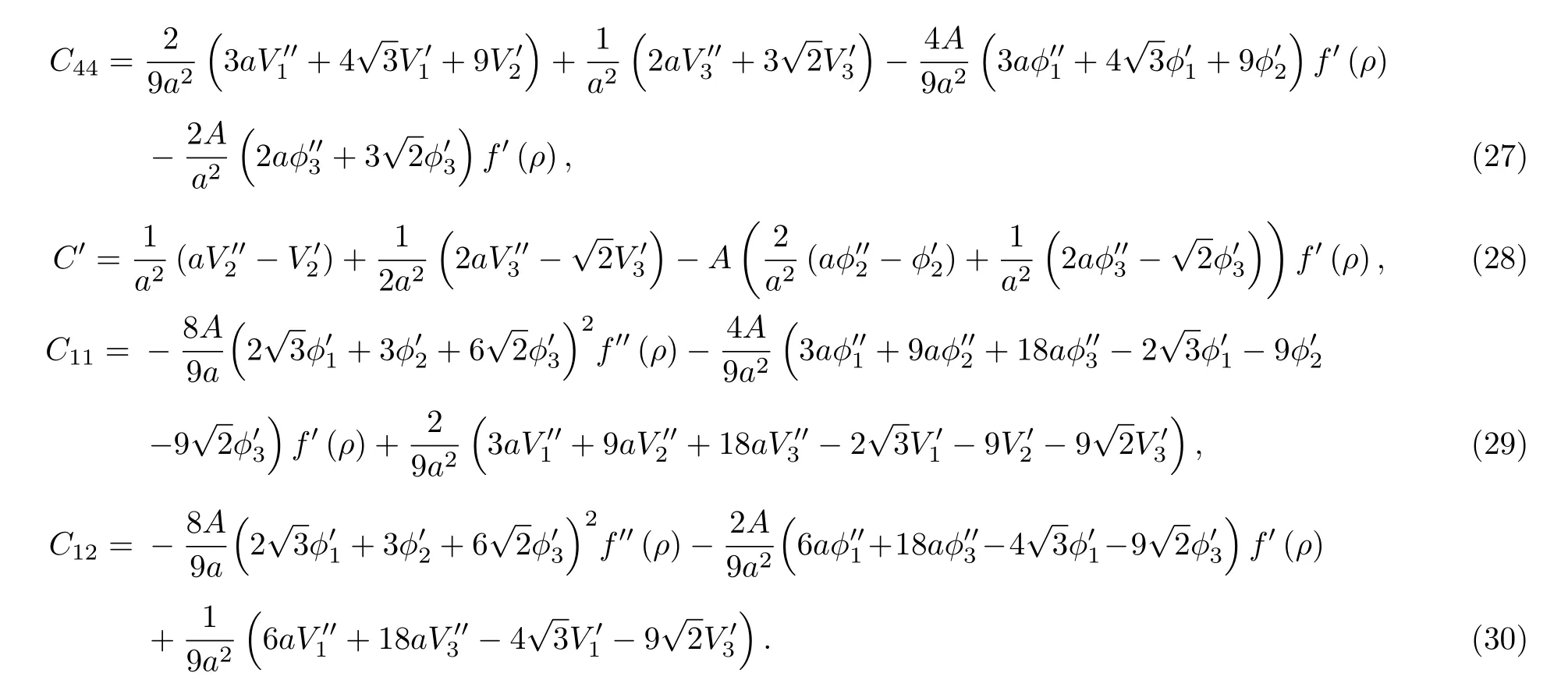
根據(31)式給出的體模量、切變模量, 柯西壓與彈性常數之間的關系, 可在這些量之間相互計算,

5 原子間勢擬合
勢函數表達式(3)式和(6)式中的c0,c1,c2,A是勢函數參數, 本文通過擬合金屬Nb的內聚能、平衡點陣常數、體模量、表面能及空位形成能的實驗數據獲得, 實驗數據[2]見表2中第1行數據.
根據第4節中建立的晶體性能與勢函數的關系, 然后采用均方差最小方法, 調整勢函數參數的大小, 使得勢函數能再現這些晶體性能, 擬合得到的原子間勢參數見表3中第1行數據, 使用所得的原子間勢計算的晶體性能列于表2中第2行.
從表3可以看出, 擬合的均方差非常小, 因此,利用所建原子間勢計算的晶格常數、內聚能、未弛豫空位形成能、 體模量的結果與實驗值完全相同,只有表面能有微小差別.
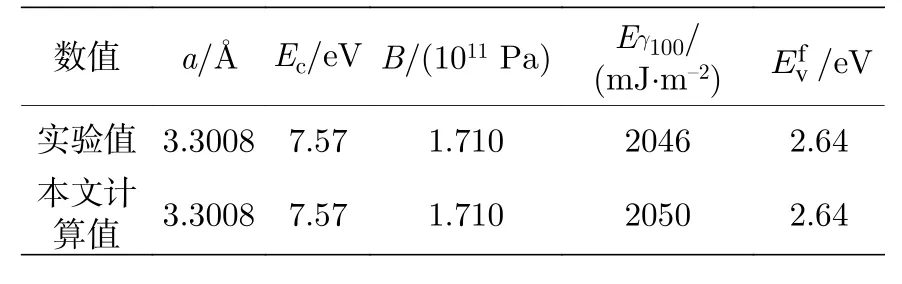
表2 擬合用金屬Nb的實驗數據及計算結果Table 2.Experimental and calculation data of metal Nb for fitting interatomic potential.

表3 金屬Nb的FS勢參數及擬合均方差Table 3.FS potential parameters of metal Nb and fitting mean square error.
6 勢函數的檢驗與應用
6.1 彈性常數
根據第3節建立的勢函數與晶體性能的關系,利用所得勢函數計算了金屬Nb的3個獨立的彈性常數及柯西壓力.結果見表4中第2行數據.從表4中數據可以看出, 除了C44偏差較大外, 其余結果均較接近實驗值.
6.2 間隙形成能
根據第3節建立的勢函數與晶體性能的關系,利用所得勢函數計算了Nb的不同間隙構型的間隙形成能, 結果見表5.其中, FS(87)一列數據是文獻[22]作者使用修正的FS勢計算的弛豫的間隙形成能.為了便于與本文的數據進行比較, 本文使用文獻[22]的勢函數計算了各種間隙構型的未馳豫間隙形成能, 列于表4中“FS(87)未弛豫”一列.
從表5可以看出, 各種方法計算的間隙形成能中, 或者〈110〉啞鈴構型的間隙能最低, 或者是〈111〉啞鈴構型的最低, 本文的計算結果也是〈110〉啞鈴構型最低.但是本文的計算結果普遍偏大, 分析其原因, 一方面我們的計算結果均未進行弛豫,另一方面, 說明我們所建的勢函數在近距離處排斥力過大, 曲線偏硬.

表4 金屬Nb的彈性常數(單位為1011 Pa)Table 4.Elastic constants of metal Nb (in 1011 Pa).
7 勢函數的修正
為了使所建立的勢函數能更好地描述間隙形成能, 我們對勢函數在近距離的行為進行修正, 嘗試加入修正項進行軟化處理, 即將對勢函數表達式(6)式在第一近鄰之內減去一項,
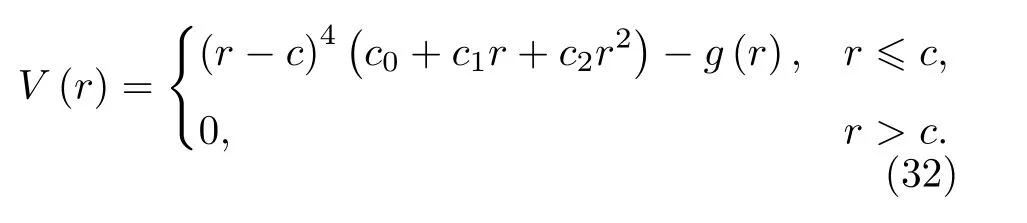
其中修正項形式如下, 且僅在第一近鄰內有效,

按照前述方法重新擬合勢參數并進行檢驗.發現加入修正項后擬合得到的勢參數幾乎沒有變化,利用修正后的勢函數計算的各構型的間隙形成能均減小, 但與文獻數據仍有一定的偏差, 為此繼續對勢函數進行修正.
將間隙形成能的計算值[24]作為目標值, 調整修正項的冪次, 當取修正項形式為(34)式時, 計算結果接近目標值.
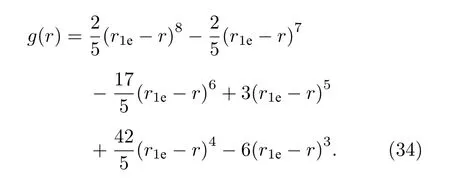
修正前后的對勢曲線、有效對勢曲線及電子密度曲線如圖2所示, 為了便于比較, 同時繪出了文獻[2], 及按文獻[2]函數形式將截斷距離擴展到第三近鄰的函數曲線.

表5 金屬Nb的間隙形成能Table 5.Interstitial formation energy of metal Nb.
由圖2(b)和圖2(c)可以看出, 原始勢函數曲線(文獻[2])在近距離處表現出吸引行為, 文獻[21]通過在小于第一近鄰范圍疊加一項B(b0—rij)3exp(—αrij)函數來增加排斥力, 修正了這種偏軟現象, 其中B,b0,α為勢參數; 文獻[22]通過對比分析由原子間勢計算的力和實驗數據之間的差別, 在小于第一近鄰范圍疊加了一項K(r1e—rij)n函數, 修正了原函數在近距離偏軟的現象, 其中K和n為勢參數.

圖2 勢函數曲線 (a) 電子密度曲線; (b) 對勢曲線; (c) 有效對勢曲線Fig.2.Potential function curve: (a) Electron density curve;(b) potential curve; (c) effective pair potential curve.
我們知道, 從能量對距離的導數可以獲得力,從曲線形狀來看, 能量曲線的斜率越大, 排斥力越大.從數學上考慮, 對于函數(x0—x)n來說,x<x0時, 隨著n的增加, 曲線的斜率將越來越大, 因此,通過幾項冪函數的迭加形成的多項式可以獲得比較滿意的曲線形式.由于近距離處的原子之間相互作用對間隙能的影響較大, 因此本文將間隙形成能作為目標值, 通過調整多項式的冪次及系數, 最終得到(34)式的修正項, 使用獲得的加修正項的Nb勢函數計算的間隙形成能接近理論計算結果.
8 討 論
8.1 函數形式對勢函數性能的影響
從勢函數與晶體性能的關系表達式可以看出,勢函數值及勢函數的一階、二階導數值對材料性能的各個物理量的影響.如: 從(11) 式、(20)式可以看出對勢函數、電子密度函數在第一、二、三近鄰處的斜率對壓力P、平衡條件有影響; 從(13)式、(27)式—(30)式可以看出對勢函數、電子密度函數、以及多體相互作用項f(ρ)在第一、二、三近鄰處的斜率、曲率對體模量B及彈性常數有影響; 從(15) 式—(18)式及(21)式可以看出對勢函數、電子密度函數, 以及多體相互作用項f(ρ)在第一、二、三近鄰處的值對與能量相關的物理量, 如表面能、空位能等有影響.比較擬合所得勢函數計算的各物理量與實驗值或理論值來修正勢函數曲線.如本文中根據間隙能的結果調整對勢曲線在近距離的行為, 進而達到修正勢函數的目的.
本文也嘗試以修改勢函數曲線形式來考察擬合結果的變化.原始文獻[2]電子密度函數及對勢函數形式為


為方便討論, 幾種函數形式的截斷距離均選取如下形式:使用不同形式的電子密度函數及對勢函數形式利用表2中的實驗數據擬合獲得的勢函數參數見表6.
由表6可以看出, 前3組數據的擬合參數不同, 是因為函數形式不同.后3組的勢參數完全相同, 是由于本文在擬合勢參數時使用的擬合數據a,及都是平衡態下的數據, 這些數據只與平衡態下曲線在第一、二、三近鄰處的值、斜率及曲率有關, 而后三組勢函數只對小于第一近鄰部分的曲線進行修正, 這種修正并沒有改變曲線在第一、二、三近鄰處的值、斜率及曲率, 因此擬合獲得的勢函數參數沒有改變.也就是說, 當使用平衡態下的數據作為擬合數據時, 調整勢函數曲線只要不改變曲線在各個近鄰處的值、斜率及曲率, 擬合的勢參數就不變.
使用獲得的各個勢函數計算表1中的晶格常數、表面能、空位能及體模量在均方差范圍內與實驗數據一致.除擬合數據之外的各物理量的計算結果見表7.
從表7可以看出, 第1列數據與表4的彈性常數及表5的間隙形成的計算值相差懸殊, 特別是C'出現了負值的情況, 表明原始的勢函數形式不適合于擴展到第三近鄰.第2列數據修改了原始的對勢函數, 將四次多項式修改為六次多項式, 保持電子密度為原始函數形式, 結果有所改善, 但與實驗值相比仍然相差很大.第3列為本文提出的函數形式, 將電子密度修改為四次冪的形式, 將對勢修改為六次多項式的形式, 彈性常數的結果有了明顯的改善, 但是間隙形成能的結果仍然遠高于實驗值.第4列和第5列數據為分別使用(33)式和(34)式對本文的對勢函數進行了修正, 也就是對小于第一近鄰部分的對勢曲線進行了軟化, 結果表明對彈性常數幾乎沒有影響, 原因與前述對勢參數的影響相同, 本文這種對對勢函數在近距離處的軟化處理并沒有改變對勢曲線在第一、二、三近鄰處的值、斜率及曲率, 而平衡態下的彈性常數只受平衡態下原子間勢函數在各個近鄰的值、斜率及曲率的影響,因此這種修正對彈性常數的計算結果沒有影響.第4列數據的間隙形成能與前3列數據相比明顯降低, 而第五列數據為根據間隙能的實驗結果對本文的對勢函數進行的進一步修正的結果, 可以看出間隙形成能稍高于實驗數據, 這是可以理解的, 因為本文計算的間隙能是未弛豫的.表明本文的這種軟化修正影響間隙能的結果.這是由于間隙原子與近鄰原子的距離往往小于bcc結構的第一近鄰, 而近距離排斥力大, 表明晶體比較硬, 這時向晶體中放入一個間隙原子將需要大的能量; 當排斥力減小時, 表明晶體變軟, 這時向晶體中放入一個間隙原子所需要的能量將減小, 因此間隙能降低.

表6 不同函數形式的勢參數Table 6.Potential parameters of different functional forms.

表7 不同函數形式的各物理量計算結果Table 7.Calculation results of each physical quantity in different function forms.
8.2 截斷距離對勢函數性能的影響
為了考察截斷距離對勢函數性能的影響, 本文使用修正后的勢函數形式即(5)式, (32)式和(34)式, 計算不同截斷距離下各物理量的變化.先保持電子密度函數的截斷距離不變, 選擇不同的對勢截斷距離, 分別擬合勢函數, 再利用所得的勢函數計算材料的各種物理量, 對勢函數的截斷距離形式為:

當x分別取0.55, 0.7, 0.80時, 各種物理量的計算結果如表8所示.

表8 不同對勢截斷距離下的各物理量計算結果Table 8.Calculation results of each physical quantity under different pair potential cutoff distance.
表8中前4行數據為擬合數據, 在均方差范圍內與實驗結果一致.第5—9行為與力學性質相關的數據, 幾種截斷距離下, 結果差別不明顯.后6行數據為間隙能的計算結果, 可以看出, 間隙形成能變化不明顯, 但x= 0.8時的均方差最小.
隨后, 本文先保持對勢函數的截斷距離c=不變, 選擇不同的電子密度函數的截斷距離, 分別擬合勢函數, 再利用所得的勢函數計算材料的各種性能, 電子密度函數的截斷距離形式為

當y分別取0.45, 0.50, 0.60時, 各種物理量的計算結果如表9所示.

表9 不同電子密度截斷距離下的各物理量計算結果Table 9.Calculation results of each physical quantity under different electron density cutoff distance.
從表9可以看出, 前4行數據為擬合數據, 在均方差范圍內與實驗結果一致, 其余彈性常數及間隙形成能的結果均變化不大, 在本文的情況下, 電子密度的截斷距離對勢函數的性能影響不大.本文的截斷方式沒有改變曲線在各個近鄰處的值、斜率及曲率, 并且本文沒有計算晶體被壓縮和拉伸等情況, 由于在各個近鄰原子范圍內沒有出現原子數的變化, 因此截斷方式對計算結果幾乎沒有影響.但是如果采取其他方式對函數進行截斷, 如(9)式的形式, 則不同的截斷距離對曲線的斜率和曲率有影響, 進而對各物理量的結果將會產生影響.另外,如果計算拉伸等體積或形狀有變化的情況, 如果截斷距離使相同近鄰原子內的原子數發生變化時, 對計算結果也將產生影響, 為此進行這類計算時, 截斷距離的選取需要慎重.
9 結 論
本文從文獻[2]的FS勢出發, 將原子間的相互作用擴展到第三近鄰,構造了過渡金屬Nb的原子間勢,并較詳細地敘述了開發原子間勢的方法.研究了勢函數曲線形式對晶體性質的影響, 同時研究了函數形式、截斷距離的選擇對材料性質的描述及勢函數質量的影響.得到如下結論.
1) 原始的FS勢函數形式不適合原子間相互作用擴展到第三近鄰.經過分析及嘗試發現, 修正電子密度函數為四次冪的形式, 對勢函數形式為六次多項式的形式時, 原子間勢能較好地描述原子間的相互作用.
2)以間隙形成能的結果作為目標值修正了對勢函數在近距離的行為, 修正后的勢函數給出了接近DFT計算結果的間隙形成能.
3)當使用平衡態下的物理量作為擬合數據時,調整勢函數曲線形式, 只要不改變函數曲線在各個近鄰處的函數值、函數斜率及曲率, 對擬合的勢參數沒有影響, 對于彈性常數的結果也沒有影響, 改變近距離處曲線的形狀影響間隙能的大小.
4)在本文的截斷方式下, 改變截斷距離對勢參數和晶體性能的計算結果均沒有太大影響.
附錄A 立方晶體剪切模量與原子間勢的關系
晶體中任意一點(xi,yi,zi)距原點的距離為ri=
對于C44, 晶體中任意一點(xi,yi,zi)的彈性位移為δxi=ε12yi, δyi=ε12xi, δzi=0, 由于應變分量是小量, 故:

對于C′, 晶體中任意一點((xi,yi,zi)的彈性位移為δxi=ε11xi, δyi= — ε11yi, δzi= 0, 由于應變分量是小量, 故


對于bcc結構金屬Nb, 設晶格常數為a,Ωe=a3/2 , 考慮前三層原子, 第一層有8個原子, 坐標為距原點距離為第二層有6個原子, 坐標為 (±a,0,0) , ( 0,±a,0) , ( 0,0,±a) , 距原點距離為a; 第三層有12個原子, 坐標為(±a,±a,0) , (±a,0,±a) , ( 0,±a,±a) , 距原點距離為
先計算C44, 根據(25)式、(26)式及(1)式—(4)式可得

再計算C′, 同樣根據(25)式、(26)式及(1)式—(4)式可得
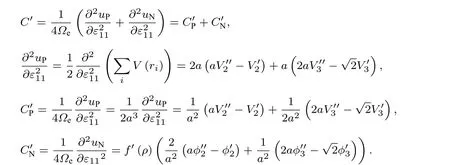
也可以采用另外一種方法計算彈性常數C11,C12和C'.
晶體的彈性變形通過彈性常數矩陣描述,
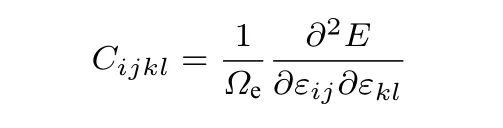
其中,E是晶體內能,εij是應變分量.
在絕對零度下, 晶體內能即是原子間相互作用勢能.
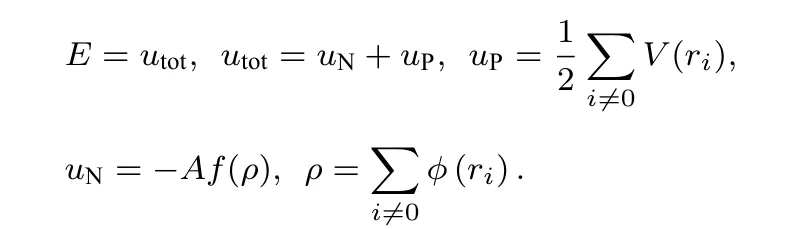
有研究表明, 在體系處于平衡態時, 依據彈性理論可以得到原子間勢與彈性常數之間的關系[25]為

其中,

(A1)式利用了平衡條件

其中,
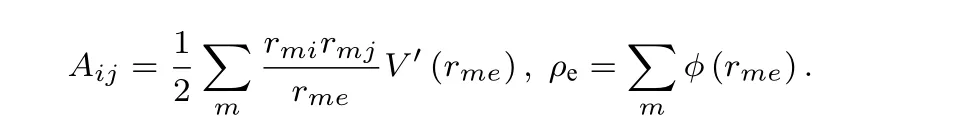
利用Voigt標記法, 可得立方晶體的彈性常數C11,C12為:

考慮原子分布情況, 對于金屬Nb, 相互作用在第三和第四近鄰之間截斷, 彈性常數C11,C12涉及的各項結果如下:
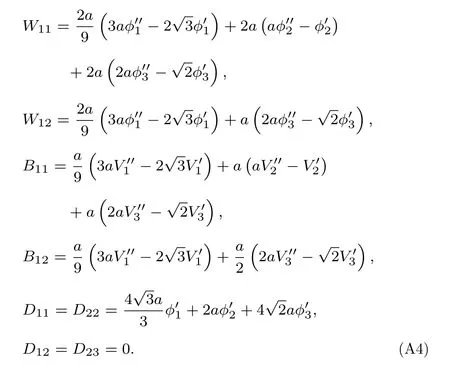

可得

由(A2)式可得



