回采巷道側(cè)向支承壓力對工作面前方支承壓力峰值和塑性區(qū)寬度的影響
吳呈哲 劉長武 趙 超3
(1.四川大學水利水電學院;2.水力學與山區(qū)河流開發(fā)保護國家重點實驗室)
在地層中開掘巷道和回采礦石時,巷道圍巖和工作面前方必然會出現(xiàn)應力重分布,一般將巷道或采場側(cè)向圍巖改變后的切向應力增高部分稱為支承壓力[1]。通常情況下,由于受到巷道和采空區(qū)的聯(lián)合作用,重新分布后的采場支承壓力的峰值位置往往位于工作面前方的拐角附近,其大小對預留礦柱的尺寸以及巷道支護參數(shù)的確定起關鍵作用。因此,研究工作面前方支承壓力的分布情況,對礦區(qū)安全開采有著重要的實際意義。
多年來,許多學者通過設計不同的力學模型,從理論層面對工作面前方支承壓力的分布情況以及塑性區(qū)的寬度進行了一系列的分析和探討。錢鳴高等[1]從平面應變角度,根據(jù)工作面前方巖體的極限平衡條件和平面微元體的受力平衡條件,推導了塑性區(qū)內(nèi)支承壓力計算公式;靳鐘銘等[2]則在此基礎上考慮了水平應力的影響,通過微元體平衡,并結(jié)合側(cè)壓系數(shù),補充了彈性區(qū)內(nèi)支承壓力計算公式;侯朝炯等[3]則認為,以上估算支承壓力的方案將工作面前方煤體簡化為平面應變問題,但卻未考慮平面應變問題所需滿足的應力微分平衡方程,因此,他從滿足應力微分平衡方程的角度出發(fā),并結(jié)合相應的邊界條件,推導出了不計體積力條件下塑性區(qū)內(nèi)支承壓力計算公式;謝廣祥等[4]則在此思路的基礎上考慮了體積力的影響,進一步推導出了塑性區(qū)內(nèi)支承壓力計算公式;袁前進[5]根據(jù)煤壁前方煤體的變形特點,將煤體劃分為破碎區(qū)、塑性區(qū)及彈性區(qū),并將煤體的變形過程劃分為塑性流動、塑性變形、彈性變形3個階段,并給出了各階段煤體強度的本構(gòu)關系,在此基礎上運用極限平衡理論推導出各區(qū)段支承壓力的理論計算公式;熊仁欽[6]認為將此問題視為平面應變問題不符合實際情況,因此用三向應力狀態(tài),結(jié)合巖體的極限平衡理論,對問題進行求解,但考慮到求解的難度,忽略了除工作面開采方向外其余2個方向上的應力增量;此外,李洪等[7]考慮了煤幫與頂板的相互作用,提出了支承壓力的彈性基礎梁計算方法;宋振騏等[8]從支承壓力的形成機理入手,通過對支承壓力形成的5個階段進行分析,創(chuàng)新地提出綜合移動角起于支承壓力邊緣的方案,建立了相關的結(jié)構(gòu)力學模型和求解方程;陳忠輝等[9]針對綜放開采煤壁前方支承壓力的分布特征,應用統(tǒng)計損傷力學建立了一個簡單的力學模型,在給定變形條件下研究支承壓力的分布規(guī)律,避免了對支承壓力的分區(qū)研究;王衛(wèi)軍等[10]在分析了沿空掘巷應力環(huán)境的基礎上,應用損傷理論,分析了給定變形下沿空掘巷實體煤幫的支承壓力分布。
在這些模型中,有學者考慮了應力重分布后所產(chǎn)生的回采巷道側(cè)向支承壓力對于工作面前方支承壓力峰值的影響,并認為回采巷道側(cè)向支承壓力的存在是導致工作面兩端巷道難以維護的關鍵因素之一[6],若不考慮回采巷道側(cè)向支承壓力的影響,會導致工作面前方支承壓力峰值和塑性區(qū)寬度的計算值偏小。因此,對于該問題的討論對實際工程有著積極的指導意義。然而,目前學者們對于相關問題的討論僅限于將工作面的前支承壓力和回采巷道的側(cè)支承壓力先分開計算后再進行簡單疊加。這種簡單疊加的方法只適用于計算工作面前方的支承壓力峰值,無法用來計算在回采巷道側(cè)向支承壓力已經(jīng)形成的情況下工作面前方塑性區(qū)的寬度。
針對上述問題,本研究基于頂板與礦幫相互作用的力學模型(即地基梁模型)[11],并綜合考慮回采巷道周圍所存在的側(cè)向支承壓力的影響,推導了相應的頂板位移計算公式,通過該公式可計算礦體的支承壓力和塑性區(qū)寬度。此外,通過相應的工程實例進行試算,進一步討論了回采巷道側(cè)向支承壓力大小對于工作面前方支承壓力峰值以及礦幫塑性區(qū)寬度的影響,為確保礦層安全開采打下基礎。
1 支承壓力理論計算
1.1 力學模型
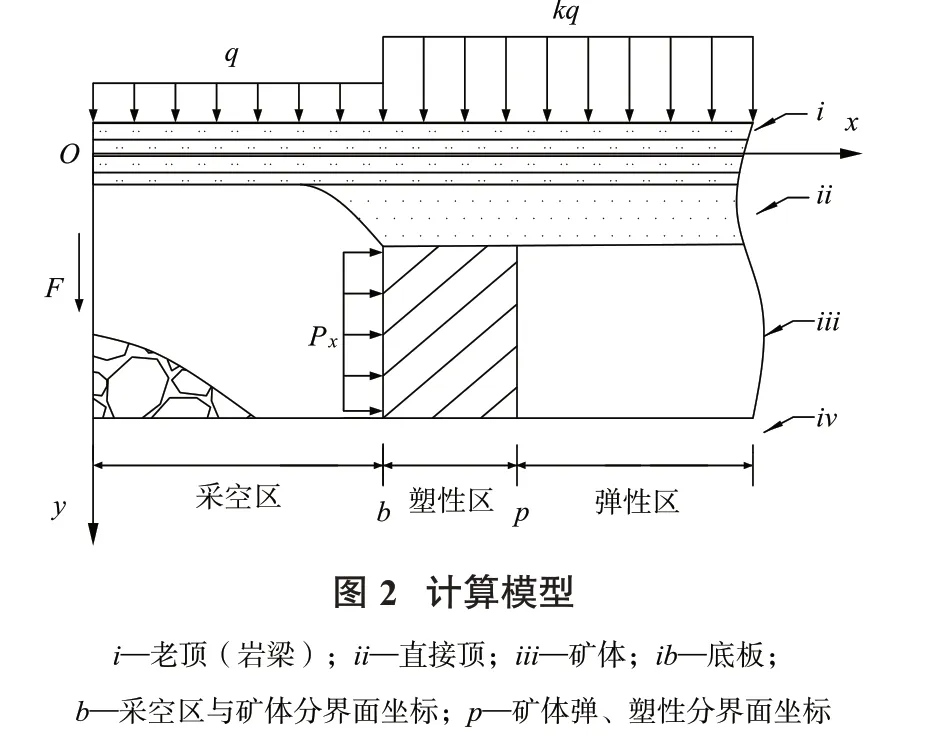
由于回采巷道開挖早于回采作業(yè),且在回采開挖前巷道周圍的支承壓力分布已趨于穩(wěn)定,因此,對于回采工作面前方支承壓力分布以及塑性區(qū)寬度問題的研究應在已處于穩(wěn)定狀態(tài)的回采巷道側(cè)向支承壓力的環(huán)境下進行分析。通過彈性力學方面的相關推導可知,開挖后巷道的支承壓力分布情況如圖1中“B-B”剖面處的支承壓力分布曲線所示。即將巷道周圍礦體劃分為彈性區(qū)與塑性區(qū),并認為支承壓力峰值位于彈性區(qū)與塑性區(qū)相交的區(qū)域。基于以上認識,本研究取巷道周圍支承壓力峰值附近的彈性區(qū)內(nèi)單位寬度的頂板以及礦體(圖1中“A-A”剖面右側(cè))來進行討論,并將側(cè)向支承壓力的影響簡化為巖梁上覆荷載的提高,即以巷道側(cè)向支承壓力的應力集中系數(shù)k來反映回采巷道側(cè)向支承壓力的影響,計算模型如圖2所示。將頂板視為巖梁,采空區(qū)位置的巖梁上方作用有均布荷載q,工作面前方位置的巖梁上方作用有均布荷載k q,礦壁上作用有工作面支護阻力P x。此外,根據(jù)鉸接巖塊假說,采空區(qū)上方巖梁端部還受到周期性垮落巖塊給巖梁帶來的作用力F。

1.2 基本假設
(1)不考慮礦層傾角、老頂自重和礦層自重力的影響。
(2)將回采巷道側(cè)向支承壓力對于巖梁、工作面前方礦體的影響綜合考慮為巖梁上部荷載的提高,即認為工作面前方礦體上的巖梁上方作用有均布荷載kq,k為巷道側(cè)向支承壓力的應力集中系數(shù),其取值受巷道尺寸、巷道形狀等因素的影響。
(3)采用地基梁假說來討論巖梁、工作面前方礦體的相互作用關系。認為塑性區(qū)內(nèi)的礦體處于極限平衡狀態(tài),彈性區(qū)內(nèi)的礦體處于彈性狀態(tài),并結(jié)合礦體中微元體的受力平衡條件對礦體塑性區(qū)內(nèi)支承壓力情況進行討論。
1.3 模型的求解
1.3.1 頂板位移曲線的建立
圖2為礦體與頂板受力模型。
在地基梁模型中,撓度與荷載、地基反力σy之間的關系為[10]
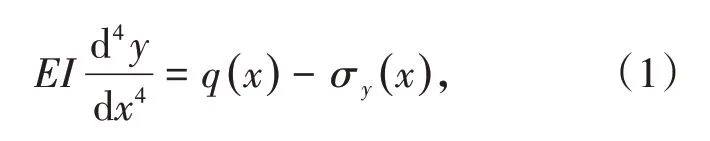
式中,E為巖梁的彈性模量,MPa;I為巖梁的截面慣性矩,m4;x為巖梁的位置坐標,m;y為巖梁的撓度,m。
根據(jù)李樹清等[12]對于礦體在彈性區(qū)、塑性區(qū)內(nèi)應力的分析可知,礦體在塑性區(qū)和彈性區(qū)內(nèi)的水平應力和垂直應力分布情況如下。
(1)塑性區(qū)。
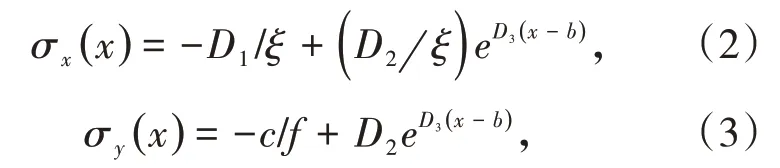
(2)彈性區(qū)。
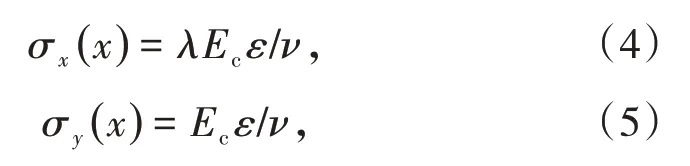
式中,ν=( 1-2μ)( 1+μ)/( 1-μ),λ=μ/( 1-μ),μ為礦體的泊松比;Ec為礦體的彈性模量,MPa。
在求得礦體彈、塑性區(qū)內(nèi)的垂直應力分布情況下,可將礦體的垂直應力視為地基梁模型中的地基反力σy(x),故計算模型可得到簡化(圖3)。
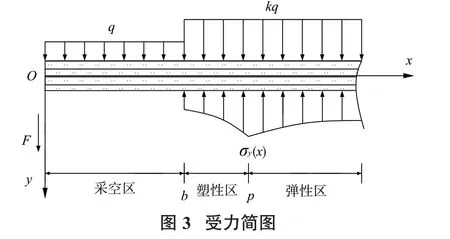
根據(jù)此受力簡圖,可將式(3)、式(5)以及各區(qū)域內(nèi)所對應的荷載條件q、k q分別代入微分方程(1)中進行求解,進而可求得礦體采空區(qū)、塑性區(qū)和彈性區(qū)上方巖梁的位移曲線。
(1)采空區(qū)上方巖梁。
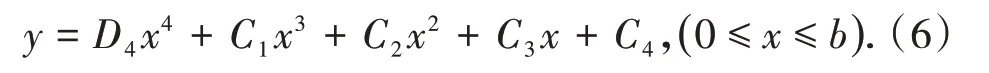
(2)塑性區(qū)上方巖梁。

(3)彈性區(qū)上方巖梁。
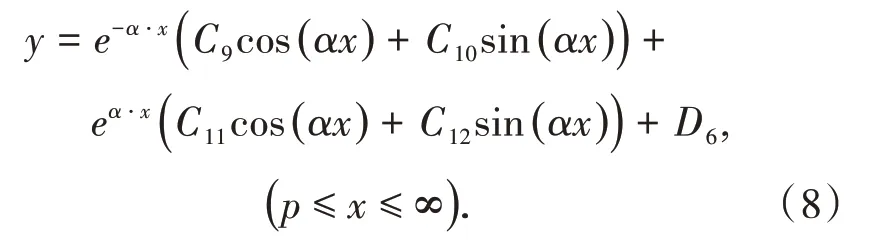
1.3.2 待定系數(shù)求解
由于總共有12個待定系數(shù),因此求解需要12個邊界條件,具體如下。
(1)采空區(qū)上方巖梁端點(x=0)處彎矩為0,剪力為F,則
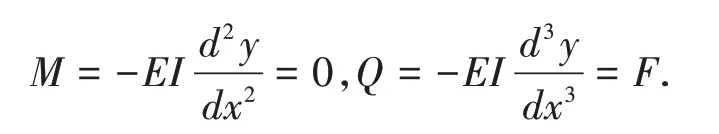
(2)采空區(qū)與塑性區(qū)上方巖梁交界(x=b)處撓度、轉(zhuǎn)角、彎矩、剪力相等。
(3)彈性區(qū)與塑性區(qū)上方巖梁交界(x=p)處撓度、轉(zhuǎn)角、彎矩、剪力相等。
(4)彈性區(qū)趨于無窮遠(x→∞)處巖梁不受采空區(qū)影響,位移趨于穩(wěn)定

將上述邊界條件代入式(2)~式(5),可求得各待定系數(shù)如下。

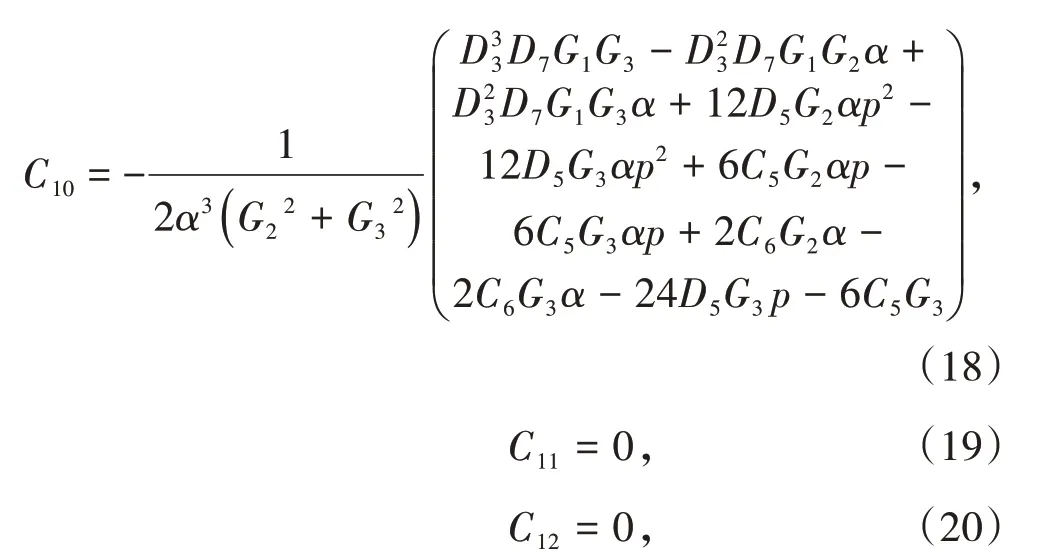
式中,G1=eD3(p-b),G2=e-αpcos(αp),G3=e-αpsin(αp)。
在實際計算中,先將相關力學參數(shù)代入式(9)~式(20)以求得待定系數(shù)C1~C12,進而將所求得的系數(shù)C1~C12代入式(6)~式(8),得到考慮了回采巷道側(cè)向支承壓力影響的頂板位移曲線。通過該位移曲線可求得頂板各點的位移值,進而可將所求得的頂板位移值代入式(2)~式(5)來求得工作面前方塑性區(qū)的寬度以及各位置的支承壓力值。
2 工程實例分析
以邢臺礦區(qū)某首采工作面為工程背景,對巷道側(cè)向支承壓力大小對于工作面前方支承壓力峰值以及工作面前方塑性區(qū)寬度的影響進行分析,相關物理力學參數(shù)見表1。其中,老頂為粉細砂巖,寬度取1 m,厚度取6 m,計算得I=18 m4。根據(jù)老頂及以上各巖層的容重、彈性模量和厚度進行估算[13],取q=0.26 MPa。周期性垮落巖塊給巖梁帶來的作用力F=535.08 kN。

?
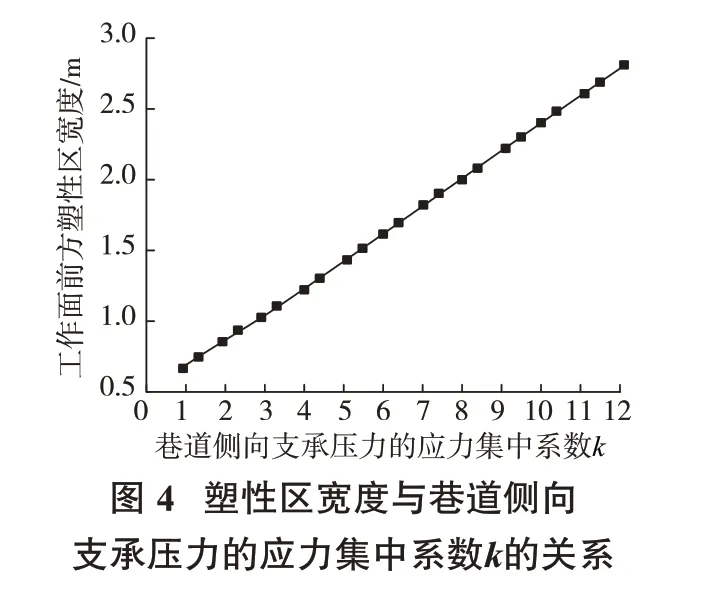
具體計算時,先通過設置一個具體的巷道側(cè)向支承壓力的應力集中系數(shù)k,再根據(jù)礦體塑性區(qū)與彈性區(qū)交界處水平應力連續(xù)這一條件求出不同k值下工作面前方的塑性區(qū)寬度,并在此基礎上計算該k值下工作面前方的峰值支承壓力大小。此外,通過設定不同的k值并分別計算該k值下工作面前方的塑性區(qū)寬度及支承壓力峰值,并對數(shù)據(jù)進行擬合,進而分析工作面前方塑性區(qū)寬度以及支承壓力峰值受k值的影響趨勢。本次計算所取的k值以0.5為公差,從1取到12,計算及擬合的結(jié)果如圖4、圖5所示。
根據(jù)圖4可以看到,工作面前方塑性區(qū)的寬度隨巷道側(cè)向支承壓力的增長而增大,且當k=1(即未考慮回采巷道側(cè)向支承壓力影響)時,塑性區(qū)寬度為0.492 m。而根據(jù)現(xiàn)場實測可知,在周期來壓條件下工作面前方的塑性區(qū)寬度為2~4 m,因此在進行塑性區(qū)寬度計算時,若不考慮巷道側(cè)向支承壓力的影響會導致塑性區(qū)寬度的計算結(jié)果嚴重偏小,不符合實際工程情況。而當k值逐漸增大后,塑性區(qū)的寬度逐漸過渡到合理的取值范圍中。但根據(jù)圖4也可發(fā)現(xiàn),只有當巷道側(cè)向支承壓力的應力集中系數(shù)k達到8以上時,工作面前方塑性區(qū)寬度才大于2 m,而根據(jù)靜水狀態(tài)下圓形巷道周圍的應力分布計算可知,巷道圍巖的應力集中系數(shù)通常達不到這么高,這主要是由于為了簡化推導,將回采巷道的影響簡化為一個應力集中系數(shù)k,若只取巷道圍巖的峰值應力集中系數(shù)來作為k值,會導致巷道的存在對于工作面前方塑性區(qū)寬度以及支承壓力的影響程度偏小,計算結(jié)果也相對偏小。因此,在取k值時建議結(jié)合壓力拱理論進行計算,比較符合本力學模型的求解。
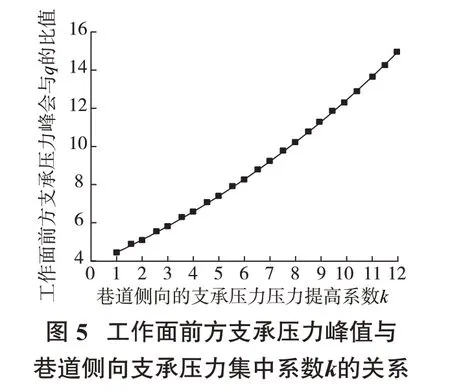
根據(jù)圖5可知,支承壓力峰值大小與原巖荷載的比值(即應力集中系數(shù))和巷道側(cè)向支承壓力集中系數(shù)k并不呈線性關系,這表明工作面前方的支承壓力峰值并不是巷道的側(cè)向支承壓力與工作面的前支承壓力分開計算后的簡單疊加。此外,工作面前方的支承壓力峰值的增長速率隨巷道側(cè)向支承壓力的增大而增大,即受巷道側(cè)向支承壓力的影響較大。
3 結(jié) 論
(1)在頂板與工作面前方礦體相互作用的地基梁模型的基礎上,考慮了回采巷道側(cè)向支承壓力的影響,推導出了相應的頂板位移公式。通過該頂板位移計算公式可計算工作面前方的支承壓力和塑性區(qū)寬度。
(2)通過工程實例計算發(fā)現(xiàn),在計算塑性區(qū)寬度和支承壓力峰值時,不考慮巷道側(cè)向支承壓力的影響,會導致計算結(jié)果偏低,不符合實際情況,因此在估算工作面前方支承壓力峰值時不應忽略回采巷道側(cè)向支承壓力的影響。。
(3)由于承壓力峰值大小與原巖荷載q的比值(即應力集中系數(shù))和回采巷道側(cè)向支承壓力集中系數(shù)k并不呈線性關系,表明在實際工程中進行工作面前方支承壓力峰值估算時,不能將支承壓力峰值視為工作面前峰值支承壓力與巷道側(cè)向峰值支承壓力的簡單疊加,而要綜合考慮兩者之間的聯(lián)系。

