改進A*算法在路徑規劃中的應用

王保劍，胡大裟，蔣玉明

1.四川大學 計算機學院，成都610065

2.四川省大數據分析與融合應用技術工程實驗室，成都610065

隨著中國制造2025的不斷推進，對我國工業制造的智能自動化提出了更高的要求。智能自動化倉庫系統作為現代工業制造的基礎，因此成為智能系統研究的熱點領域之一。其中基于自動導引車（Automated Guided Vehicle，AGV）的智能自動化倉庫系統是智能倉庫系統的重要分支。在由多臺自動導引車組成的自動導引車系統（Automated Guided Vehicle System，AGVS）的運行過程中，需要解決任務調度、路徑規劃和避碰等一系列問題[1-3]，其中AGVS的路徑規劃是研究的熱點、難點。

目前主要路徑規劃算法有Dijkstra算法[4]、A*算法[5-6]等，智能路徑規劃算法有蟻群算法[7]、遺傳算法[8]、Q-learning算法[9]等。其中A*算法是啟發式搜索算法[10]，其算法本身具有簡潔高效，能夠快速找到最優解的優點，因此被廣泛應用于AGVS路徑規劃。A*算法有很多局限性，文獻[11]提出一種結合跳點搜索算法的改進A*算法，能夠有效減少列表中無用節點數量，減少計算量，提高算法效率，解決A*算法在規模較大的AGVS中對多個AGV進行路徑規劃的應用場景中系統開銷大，路徑規劃速度慢的問題。文獻[12]在當前節點的啟發函數中加入父節點的啟發函數，使啟發函數在代價函數中的占比保持在一個合理范圍，提高算法的實時性。文獻[10]采用新的數據結構將A*算法中的搜索操作并行化，同時實現算法的快速插入操作，提升算法的效率。文獻[13]在傳統A*算法的啟發函數中引入網路負載，能夠有效均衡各網絡負載，改善出口區域負載過高的情況。但是采用模型較為簡單，只考慮特殊情形下局部網絡負載過高的情況，與實際應用場景差別較大，改進算法并不能廣泛適用于AGVS的路徑規劃。

AGV尋路過程中避開高負載節點是解決局部擁塞的關鍵。因此本文在傳統A*算法的啟發函數中，引入節點負載，從算法層面上解決了多AGV系統采用傳統A*算法進行路徑規劃時容易造成局部節點負載過高的問題，從而避免AGV系統陷入局部擁塞，提高系統效率。最后通過模擬仿真實驗，證實了改進算法的可行性。

1 問題描述

本文改進A*算法是應用在基于柵格地圖[14]的智能倉庫，智能倉庫模型如圖1所示。倉庫模型主要有以下部分：

（1）分揀臺：用于存放待分揀的貨物，AGV執行任務的起點，位于倉庫模型的最左側。

（2）道路：位于分揀臺和貨架之間，用于AGV搬運貨物。

（3）貨架：集中在倉庫模型的中間靠右側，用于存放已經分揀好的貨物。

（4）AGV：用于貨物搬運的工具，能夠根據相應的算法，把貨物從起點運送到目標節點位置。

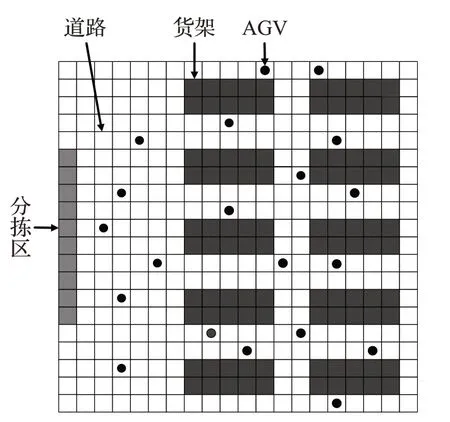
圖1 智能倉庫模型圖

以模型構建的現實性和易處理性為原則，不失一般性[15]，提出如下假設：

（1）結合智能倉庫的實際應用情況AGV的運動方向只考慮上下左右，可橫向或縱向跨越柵格[16]。

（2）不考慮AGV的裝載和卸載時間，即AGV的裝載和卸載時間均為0。

（3）AGV運行過程中速度不變，不考慮起始點出發時加速，到達目的地減速的過程。

（4）不考慮包裹到達投遞區之后的出庫過程。

（5）單個AGV只能搬運單個貨物，一個貨物也只能被一個AGV搬運。

（6）為了最大程度上避免沖突和死鎖，本文采用文獻[17]的避碰策略，任務優先級高的AGV先行，優先級低的AGV則等待。

2 A*算法

2.1 算法描述

A*算法是一種啟發式搜索算法，引入了最優啟發式函數，可以在搜索過程中避免盲目性[18]，其表達式如式（1）：

其中，AGV路徑是由各個節點組成，可通過節點集合{d1,d2,…,dn,…,dm}表示，d1表示起始節點，dn表示為當前節點，dm表示目標節點。f*(n)為代價函數，g*(n)是起始節點到當前節點的最短距離，如果g*(n)=0，代價函數所表示的算法是最佳優先搜索算法（BFS）。h*(n)是當前節點到目標節點的最短距離，如果h*(n)=0，代價函數所表示的算法是Dijkstra算法。目前是無法通過該節點預知該節點與目標節點的最短距離，因此使用h(n)代替h*(n)，因此替換過后的代價函數表達式如式（2）：

h(n)選取原則為h(n)的值不大于h*(n)，通常使用歐式距離計算公式、曼哈頓距離計算公式和切比雪夫距離計算公式，其對應表達式分別是式（3）～（5）：

2.2 算法流程

A*算法流程的核心就是維護Open和Closed兩個集合。其中Closed集合中存放的是已拓展節點，Open集合中存放待拓展節點。節點代價函數值表示該節點的優先級，選取Open集合中代價最小（優先級最高）的節點進行拓展，將已經拓展的節點存放在Closed集合中。如果目標節點出現在Open集合中，則依次返回父節點，最終規劃出一條路徑。其算法的路徑規劃過程如圖2。

其中橙色節點D1為路徑的起點，Dm為目標節點，黑色節點為障礙物，AGV無法通過障礙物節點，綠色節點為待拓展節點，白色為可通過節點。最終生成一條藍色節點的路徑。

2.3 傳統A*算法不足之處

圖2 A*算法尋路過程示意圖

在采用傳統A*算法的多AGV系統中，代價函數只考慮起始節點到當前節點的最短路徑和當前節點到目標節點的最短路徑估計。在很多應用場景中，AGV起點相對集中在一個區域，目標節點相對集中在另一個區域。若是采用傳統A*算法，只考慮距離作為單一評價方式的啟發函數，執行不同任務的AGV所行走的路徑大致相同，這會導致一部分節點繁忙，一部分節點空閑。繁忙節點負載較大，周圍常常有多個AGV需要競爭、搶占該節點，因此該節點周圍會出現等待或滯留的AGV，容易導致該區域出現局部擁塞甚至是死鎖。同樣系統中的很多空閑節點就會造成資源的浪費，系統效率低下。多AGV搶占節點如圖3所示。

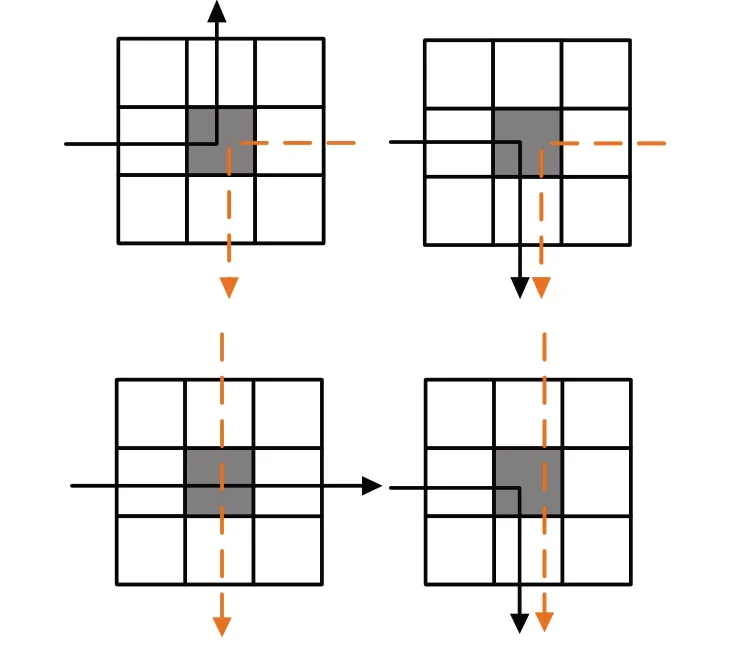
圖3 多個AGV搶占節點示意圖

圖中，箭頭表示AGV移動的軌跡，灰色節點表示有多個AGV搶占的節點。然而在傳統A*算法的啟發函數中，沒有引入節點負載，因此無法在尋路過程中避開這些高負載節點，避免局部擁塞的發生。

3 結合節點負載的改進A*算法

本文提出一種結合節點負載的改進A*算法，在傳統A*算法的啟發函數中引入節點負載，并且提出動態節點負載計算公式，能夠動態更新節點負載，有效提高算法的實時性。改進算法的表達式如式（6）：

其中，n表示尋路過程中拓展的第n個節點，f(n)是代價函數表示待拓展節點的優先級，f(n)值越大，節點優先級就越低，f(n)值越小，節點優先級就越高。g(n)是起始節點到當前節點的最短距離，l(n)是結合節點負載的節點啟發函數，μ是一個常數，對節點負載進行縮放，使算法有更好的表現，如果μ=0，該算法就變成傳統的A*算法，h(n)是傳統A*算法的啟發函數，常用曼哈頓距離或者歐式距離計算公式。k n是此時第n個節點的負載值，存儲在一個(M×N)的二維矩陣中，通過維護二維矩陣，動態更新節點負載值，負載值最低是0，其計算公式如式（7）、（8）：

其中，x表示節點負載迭代次數，k x表示第x次迭代過后的節點負載值，T x表示第x次迭代的時刻，迭代從T0時刻開始，并且T0…T x時間間隔相等，?是一個系數，G x表示T x-1～T x這段時間內所有通過該節點的AGV所花費的總時間，其計算公式如式（8）。g表示T x-1～T x這段時間內通過該節點的AGV數量，t i表示第i個AGV通過該節點花費的時間。D是節點冷卻常數，如果T x-1～T x這段時間沒有AGV或者有較少的AGV通過該節點，該節點負載就會相應減少，系統每隔T x-T x-1更新一次二維矩陣，并且節點負載值恒大于等于0。

本文提出的改進A*算法，在啟發函數中引入節點負載作為評價函數，從而節點負載影響AGV尋路過程中節點的選擇。如果節點負載較高，其相應的代價函數f(n)就會較大，對應的優先級就會較小，因此AGV在尋路過程中就會優先考慮負載較低的節點，從而均衡各個節點的負載，達到避免局部擁塞的發生，提升系統效率的目的。

中國—東盟博覽會永久落戶南寧，不僅為南寧吸引了大量的外部投資，也為南寧的旅游業帶來了充足的客源。因此，中國—東盟博覽會在推動南寧經濟的同時，也使南寧旅游業整體質量的提高。東博會和旅游業的良性互動，使得兩者融合發展，促進南寧城市競爭力。在中國—東盟博覽會的影響下，南寧的旅游業不斷向好向快發展；而南寧旅游業的完善也在一定程度上保證了東博會舉辦的質量。兩者的互動迎來社會和諧發展共贏的局面。

4 仿真實驗

4.1 環境模型

實驗采用柵格地圖對智能倉庫模型進行建模，將本文提出的改進A*算法與基于交通規則下的A*算法[19]做對比，證明改進算法能夠有效均衡各節點負載，提高系統效率。仿真模擬規則如下：

（1）生成20×20的柵格地圖，每個格子長1 m，小車的速度1 m/s。其中灰色方格表示分揀臺，為每個AGV分配貨物，黑色格子表示貨架，AGV執行相應的任務將分揀臺上的貨物運輸到指定貨架，黑色小圓點表示正在執行任務的AGV，白色格子表示AGV可以通行的區域。柵格地圖如圖1。

（2）對應地圖生成和維護兩個二維矩陣和一個系統時鐘記錄時刻T x，從T0時刻開始，并且T0…T x間隔相等。第一個矩陣用于存放公式（8）計算出T x-1～T x時間段內所有通過該節點的AGV所花費的總時間。再通過公式（7）計算生成對應的節點負載值并存放在第二個二維矩陣。每隔?T(T x-T x-1)更新一次二維矩陣，時間間隔?T設為8 s。其中，節點負載最大值為40。

（3）AGV系統生成150個任務，使用不同數量的AGV分別使用基于交通規則下的A*算法，改進算法完成任務，對應的AGV數量依次是5、10、15、20、25、30。記錄系統完成所有任務所需要的時間，AGV行走的總路程和不同時間段節點負載值。

4.2 算法對比

仿真系統分別采用基于交通規則的A*算法（簡稱算法1）和本文的改進A*算法（簡稱算法2）進行對比實驗，分別記錄AGV系統完成所有任務的總時間，單個任務完成的平均時間，AGV行走的總里程和節點負載，從不同維度對算法1和算法2進行對比。

圖4所示的是在分別采用算法1和算法2的AGV系統中，完成150個任務所需要的時間。藍色實線表示算法1，橙色虛線表示算法2。從圖中不難發現，隨著系統中AGV數量的增加，系統所花費的時間會相應減少。當系統中AGV數量超過15個時候，兩種算法都趨于緩和，但算法2優于算法1，總的系統消耗時間比算法1減少了16.18%。

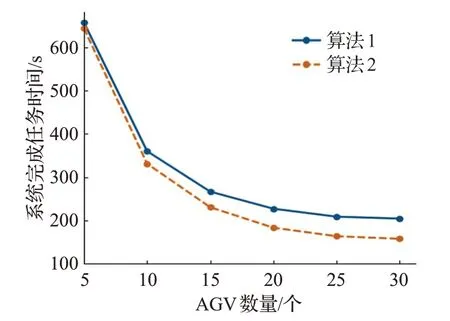
圖4 AGV系統完成任務總時間

圖5 所示的是擁有不同AGV數量的AGV系統完成單個任務所需要花費的平均時間。隨著系統中AGV數量的增加，完成單個任務的平均時間增加。當系統中有較多AGV時，多個AGV搶占節點的概率增加，根據公式（7）、（8），被搶占節點負載增加，從而被搶占節點所在區域中會出現多個AGV等待下一節點釋放或一直未能搶占到下一節點而滯留父節點的現象，使得該區域節點負載增加，導致局部擁塞，甚至死鎖，大大降低系統效率。算法2在尋路過程時能夠有效避開高負載節點，對比算法1能夠減少14.24%的時間開銷。

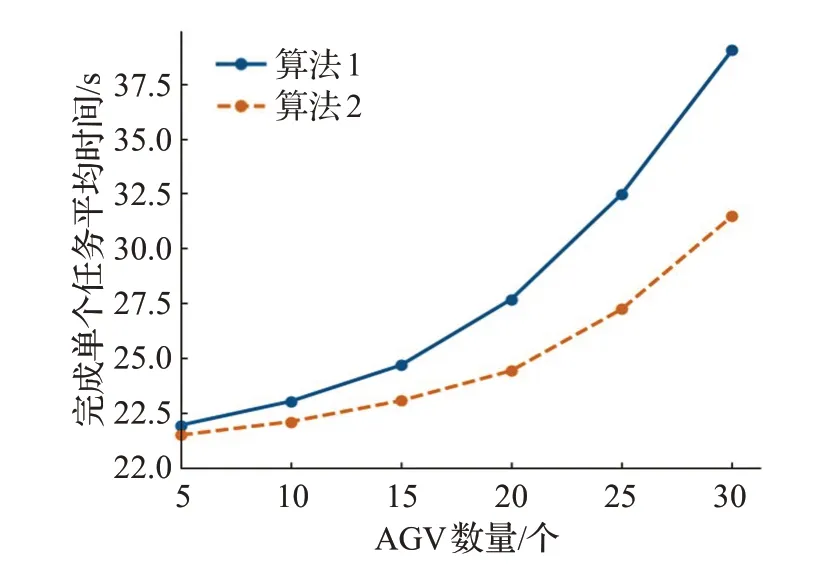
圖5 完成單個任務的平均時間

圖6 所表示的是在AGV系統中，完成所有任務AGV行走的總里程。在采用算法1進行路徑規劃的AGV系統中，隨著系統中AGV數量的增加，AGV行走的總里程變化較小，維持在一個特定值附近。然而在采用算法2的AGV系統中，AGV行走總里程隨著系統中AGV數量的增加而相應增加，在算法1的基礎上增加了4.67%。這是因為改進算法在算法1的代價函數中引入節點負載，AGV在尋路過程中會避開高負載節點，沒有選擇最短路徑，犧牲了路徑長度，減少時間開銷，提高了系統效率。

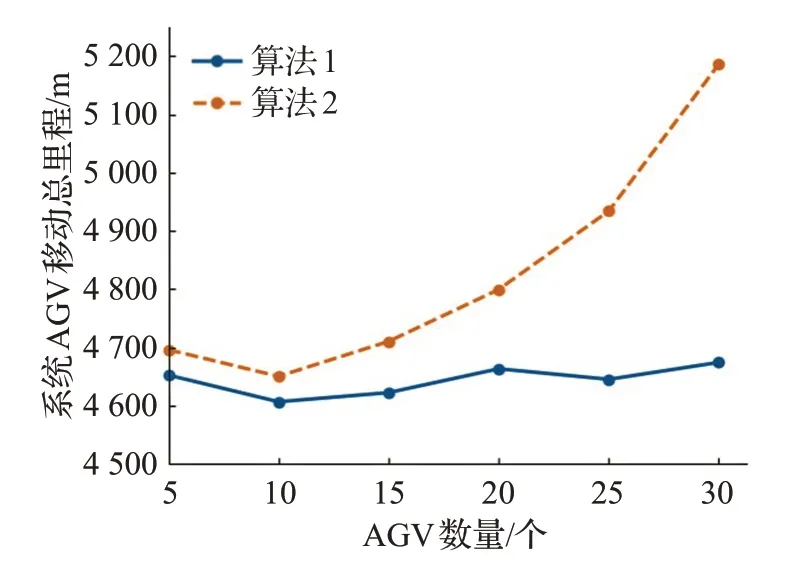
圖6 AGV移動總里程

表1對比了算法1和算法2的節點負載情況，系統中AGV數量為30，時間是系統開始運行后80 s。算法2雖然平均負載值相對算法1增加了5.45%，但標準差減少了－29.93%，說明改進算法能夠有效避開熱點節和利用低負載節點，均衡各節點負載。

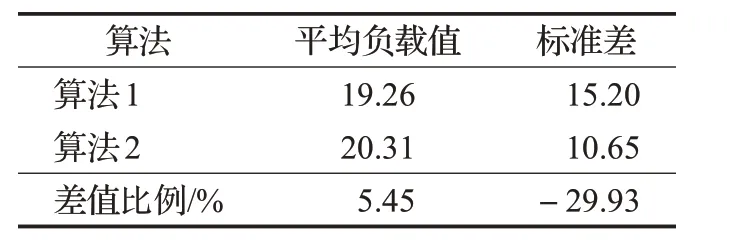
表1 節點平均負載和標準差表

5 結束語

本文提出一種結合節點負載的改進A*算法，在啟發函數中引入節點負載，對比基于交通規則下A*算法，雖然增加了系統中AGV行走的總路程和節點平均負載，卻換了更少的時間開銷，以及提高了單個任務的執行效率。通過仿真實驗能表明改進A*算法能夠有效避開高負載節點，均衡各節點負載，避免局部擁塞，提高系統運行效率。