顧及各向異性的多參數協同優化IDW插值方法

顏金彪，吳 波，何清華

1. 江西師范大學地理與環境學院，江西 南昌 330022； 2. 衡陽師范學院傳統村鎮文化數字化保護與創意利用技術國家地方聯合工程實驗室，湖南 衡陽 421002

在地學研究中，通常需要具有一定規則的面狀數據。然而，很多可獲得的地學數據都是站點采集的，呈現離散和不規則的分布[1]。這就經常需要利用空間插值技術將不規則的離散數據轉換成規則的面狀空間數據。

空間插值是通過有限的離散采樣點來建立某種插值函數關系，并將待插值點一定范圍內的已知采樣點代入該函數表達式來獲得該插值點的屬性值[2]。常用的插值方法包括克里金插值方法、自然鄰域法、趨勢面法及反距離加權插值(inverse distance weighting,IDW)等。由于IDW插值原理簡單、計算簡便且符合地理學第一定律[3]，在各學科領域都得到了廣泛應用[4-7]，被認為是GIS領域中一種標準的空間插值方法。盡管在多數情況下IDW插值方法都能取得較好的效果，但由于地學數據的復雜性，其插值效果還有待進一步提高。

近年來，人們從最鄰近點數、距離衰減系數以及空間鄰近度[8]等幾方面提出了各種改進算法，改善了IDW空間插值精度及其適用性。在如何選擇最鄰近點數方面，文獻[9]認為利用14個最鄰近的點進行IDW插值是合適的，而文獻[10]認為用5個最鄰近點就可以得到滿意的結果。其次，文獻[11]在評估城市噪聲地圖時發現距離衰減系數α=4比α=1能獲得更加準確的噪聲分布地圖；文獻[9]認為不同的α值將有不同的插值結果，并建議通過多次試驗來選擇參數α。文獻[10]認為在研究區內的不同地點可能存在不同的距離衰減關系，并開發了一種自適應IDW方法(AIDW)，允許參數α根據鄰近采樣點的空間模式變化。在算法參數的優化方面，現有方法或者僅考慮單參數對IDW插值的影響，或者依次對各參數進行獨立優化，都難實現模型插值精度的整體優化。文獻[7]固定距離衰減系數為2，利用交叉檢驗(cross validation，CV)[12]去優化得到最鄰近點數；文獻[9]固定最鄰近點數為14，利用CV去優化距離衰減系數，但候選的距離衰減系數僅有3個可選值。考慮到IDW的插值精度受到多個參數的影響，部分參數獨立調優難實現插值模型的整體優化，因此，實踐上需要提供一種智能化程度較高的多參數協同優化方法。

經典的IDW假設地理事物的分布呈現各向同性[13]的特點，因而通常采用歐氏距離來表達空間鄰近度。由于地理事物分布的復雜性，其分布往往呈現各向異性[14]的特點，如氣溫呈現出明顯的經緯度方向性，使得各向同性的距離度量難以反映氣溫在經緯度方向的不同變化。文獻[15]將歐氏距離轉變為待插值點與參考樣本點的最短路徑距離來重新定義空間鄰近度；文獻[16]提出采用一種“橢圓”距離來處理各向異性的插值問題，文獻[17]提出了一種基于最短風場路徑的復雜距離來表征城市風場對顆粒物濃度分布的影響；針對河道各向異性的復雜地形，文獻[18]采用最短時間距離來替代歐氏距離；顧及電離層分布的經緯度方向異性，文獻[19]重新定義空間鄰近性后獲得了更高精度的電離層插值效果。目前已有的研究大多情況針對特定應用場景來改進算法，并通過重新定義空間鄰近度來提高IDW的插值精度，需要額外的輔助數據(如風速、流速等)來定義各向異性的空間鄰近度，制約了這類方法的普適性應用。

本文提出一種顧及空間各向異性的多參數協同優化IDW插值方法(PIDW)。首先，引入具有物理意義的距離及方向調節參數來反映地理現象的各向異性，將典型的歐氏距離擴展為各向異性的“橢圓”距離；然后，基于CV準則構造了適合于PIDW插值算法的適應度函數，并采用粒子群算法對PIDW插值模型的多個參數進行協同優化，實現PIDW插值效果最佳的目的。

1 PIDW算法

PIDW是一種顧及各向異性的IDW插值的改進模型，通過引入距離及方向調節參數來描述空間點間各向異性的鄰近性關系，并利用粒子群優化算法實現模型的多參數協同優化。圖1是PIDW方法的主要流程，其算法主要包括四參數協同優化以及插值兩大過程。

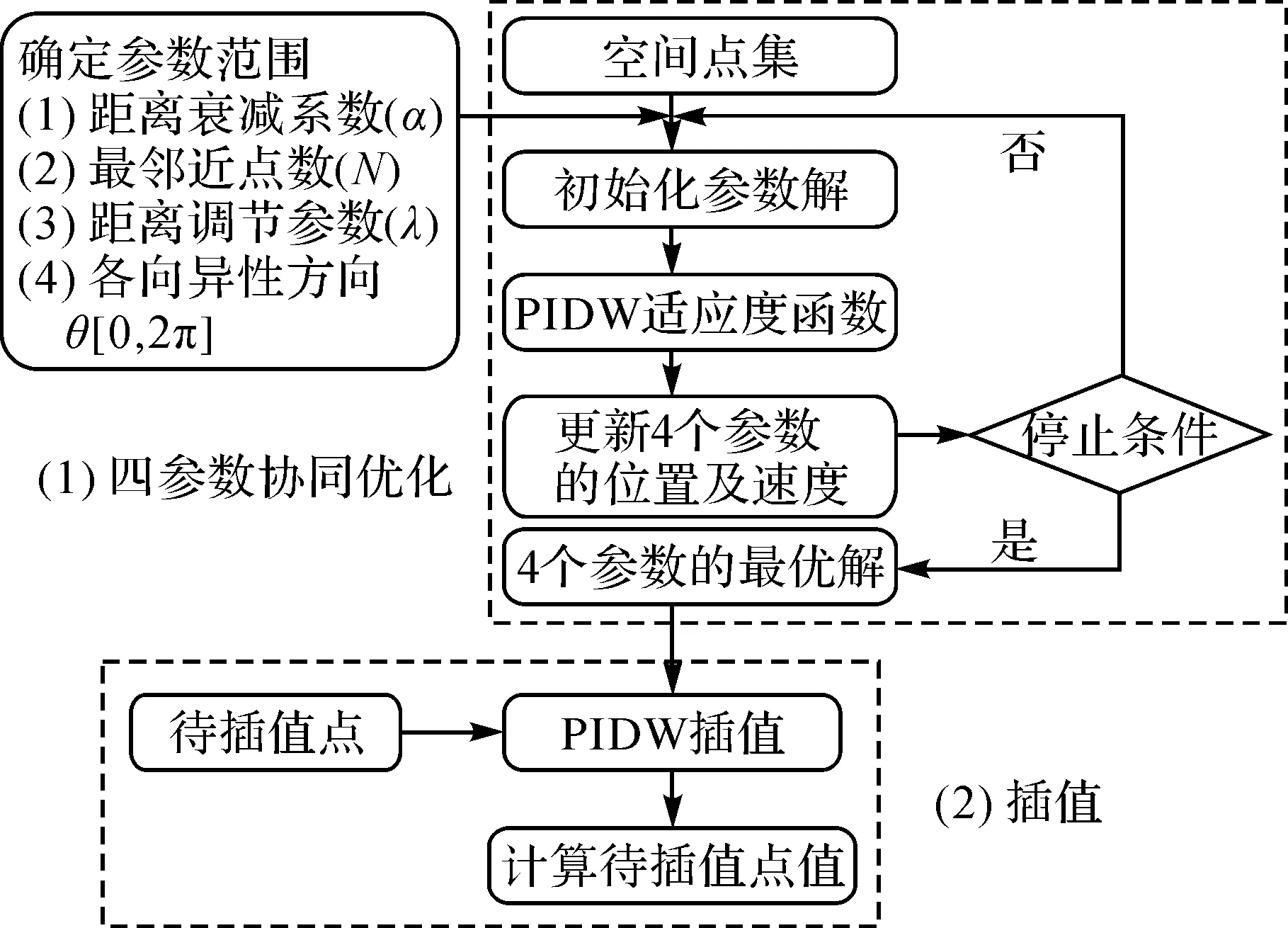
圖1 PIDW方法的流程Fig.1 The flowchart of the proposed PIDW method

1.1 各向異性表達模型

IDW插值模型如式(1)所示

(1)

式中，i代表任意待插值點；zj為點j處的實測值；Sij是未知點i與已知點j之間的距離；N為最鄰近點數；α為距離衰減系數。

(2)

式中，(Xi,Yi)與(Xj,Yj)表示點i與j的笛卡兒坐標。

由式(2)可知，當λ等于1，那么Sij將等價于歐氏空間距離；當λ>1，如果兩點之間ΔY越大，那么兩點Y方向之間的距離將更遠，即Y方向的空間鄰近性減弱；反之，當λ<1，那么兩點之間X方向的距離相對將增大，即兩點的X方向的空間鄰近性將減弱。如圖2所示，距離調節參數λ能夠改變最鄰近點的選擇，其中圖2(a)為均質空間下所選擇的空間鄰近點，圖2(b)為顧及各向異性時選擇的空間鄰近點。

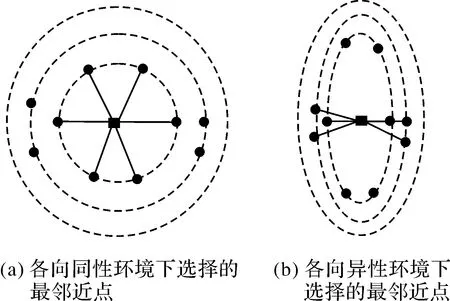
圖2 各向同性與各向異性環境下最鄰近點的選擇Fig.2 Illustration of the different selection of proximity points in the cases of isotropic and anisotropic assumptions

式(2)蘊含了數據的各向異性方向正好沿著數據的坐標軸，這與大多數的實際情況不符。因此，需要進一步引入方向參數θ來描述一般情形下的各向異性，從而可以建立原始坐標與反映各向異性坐標的轉換關系，如式(3)所示

(3)

結合式(2)、式(3)，可以得到式(4)

(4)

式中，Eij表示待插值點i與樣本點j之間顧及各向異性的距離；λ用于調節坐標系統下不同坐標軸的距離；θ∈(0,2π)表示原始坐標與各向異性坐標系的旋轉角度；ΔX與ΔY為原始數據中待插值點與已知樣本點之間的歐氏距離。

1.2 基于粒子群的多參數協同優化

考慮到影響IDW插值效果由距離衰減系數、最鄰近點數、距離調節及方向參數共同決定，參數的確定本質上是一個多元變量的尋優過程。本文提出采用粒子群智能優化搜索算法[20]，通過CV方法構造粒子群優化的適應度函數，將多變量的優化問題轉化為求解函數的極值問題，從而實現插值精度偏差與方差的總體滿意效果。

1.2.1 粒子群算法

粒子群算法采用群體智能優化策略。首先，給空間中所有粒子分配初始隨機位置和速度；然后，根據每個粒子的速度、問題空間中已知的全局最優位置和粒子已知的最優位置依次更新每個粒子的位置，通過種群內粒子間的合作與競爭機制來進行全局優化獲得最優解。在D維空間中，設定粒子群數為Q，粒子i的位置表示為xi=(xi1,xi2,…,xiD)，粒子i的速度為vi=(vi1,vi2,…,viD)，pbesti=(pi1,pi2,…,piD)表示粒子i經歷過的最佳位置，gbest=(g1,g2,…,gD)表示所有粒子的全局最佳位置，f(xi)為適應度函數[20]。其中粒子i的第d維位置和速度更新方法分別如式(5)、式(6)所示

(5)

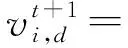
(6)

1.2.2 適應度函數

粒子群算法的多參數優化問題關鍵在于確定適應度函數。為了降低可能的過擬合現象[21]，導致插值精度偏差與方差的背離，本文利用CV檢驗方法來構造PIDW算法的適應度函數，如式(7)、式(8)所示

(7)

xi=argminf(xi)

(8)

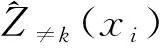
1.2.3 算法流程

1.2.3.1 確定4個參數(α,λ,θ,N)的組合解

(1)給定粒子群算法的初始化條件，搜索維度D=4(α,λ,θ,N)，α、λ、θ、N的搜索區間分別為[1，5]、[0.01，100]、[0，2π]及[4，30]，其中參數N和α的搜索范圍是在參考文獻[9—11]的基礎上設定的，距離調節參數λ的范圍根據經驗確定，而角度參數θ的范圍為所有可能的取值。采用隨機初始化種群的方法產生一組包含(α,λ,θ,N)的解集合。

(2)計算粒子的適應度值。將每個粒子的xi代入式(7)的適應度函數，得到每個粒子的f(xi)。

(3)獲取粒子i的個體最優值pbesti。對每個粒子，用其f(xi)值和個體最優位置Pbest(i)比較，如果f(xi)優于Pbest(i)，則用當前待優化參數的位置xi更新個體歷史最佳位置Pbest(i)。

(4)獲取群體的全局最優值。對每個粒子，將其當前f(xi)與全局最佳位置Gbest做比較，如果當前的適應值更佳，則用當前粒子的位置更新全局最佳位置Gbest。

(5)根據式(5)和式(6)對粒子的速度和位置(包括距離衰減系數、最鄰近點數、距離調節參數以及各向異性方向)進行更新。

(6)如未滿足粒子群算法的終止條件，則返回步驟(2)。本文設定迭代次數達到200或者最佳適應度值的增量比值少于1e-6時算法停止。

(7)輸出最佳位置xi，即使得適應度函數值最佳時的距離衰減系數、最鄰近點數、距離調節及各向異性方向參數。

1.2.3.2 插值

根據粒子群算法優化得到的參數組合解(α,λ,θ,N)，代入IDW插值模型(式(1))中獲取待插值點屬性值。式(1)中Si的計算方式采用本文顧及各向異性方向的“橢圓”距離計算方式Eij(式(4))，其中α、N、λ、θ分別為優化得到的距離衰減系數、最鄰近點數、距離調節及各向異性方向參數。

2 試 驗

本文使用不同分辨率的全國氣溫站點與黃河堤壩數據來驗證PIDW算法的可行性，并將PIDW插值算法與經典的反距離平方加權(classical IDW,CIDW)、四象限IDW(four quadrant IDW,FIDW)[22]、自適應的反距離平方權重(adaptive IDW,AIDW)[23]、K近鄰反距離平方加權(K-nearest neighbor adaptive IDW,KAIDW)[2]、普通克里金(ordinary Kriging，OK)以及顧及各向異性的克里金(anisotropic Kriging,AnisOK)進行對比試驗。

(9)

(10)

(11)

2.1 年均氣溫插值試驗

數據來源于中國氣象中心2005年的682個氣象站點的觀測數據。通過前期的數據預處理，剔除少量觀測臺站儀器出現故障的數據，對每個臺站的日平均氣溫求和，最終獲取各個臺站的年平均氣溫。由于氣溫與海拔存在約0.6℃/100 m的比例關系，本文根據氣象站臺的海拔數據，將每個氣象站臺的年平均氣溫歸算到海平面。這樣處理的理由是剔除不同高程對年均氣溫的影響，著重討論經緯度變化對氣溫差異的影響[26](圖3)。

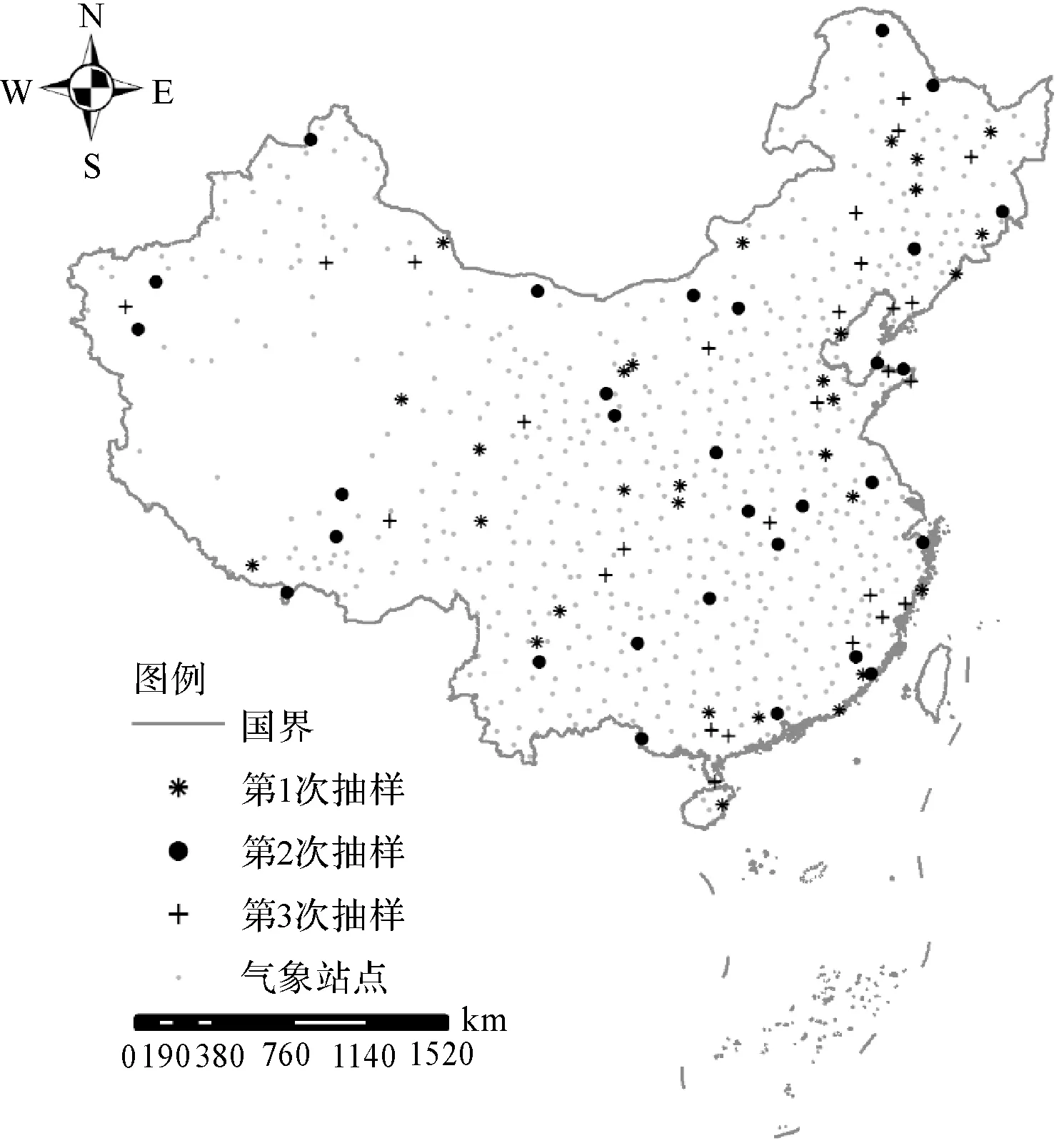
圖3 氣象站點的分布Fig.3 Spatial distribution of national weather stations

為減少樣本選擇的影響，本文重復進行了3次隨機抽樣，其中每次從總體中抽取30個作為測試集，其余作為訓練集。圖3中“*”“·”及“+”形代表3次隨機抽樣的樣點分布。經過PSO優化，PIDW的距離衰減系數α為1，最鄰近點數N為7，距離調節參數λ為0.26，各向異性方向θ為0.02°。將計算結果的平均值作為插值精度的最終評價值。7種算法的對比結果如圖4所示。

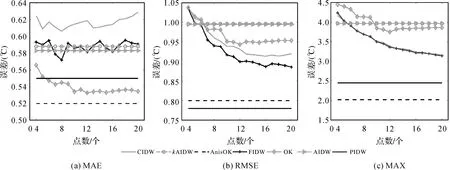
圖4 利用MAE、RMSE及MAX指標評價7種算法的插值精度Fig.4 Comparisons the accuracies of seven different algorithms using MAE,RMSE and MAX measures

從圖4(a)可以發現：CIDW與FIDW插值算法的MAE隨著插值點數的增多呈現震蕩式變化，并且FIDW的MAE顯著低于CIDW；KAIDW、AIDW與FIDW的MAE大致保持一致，但OK和PIDW的MAE顯著低于KAIDW、AIDW、FIDW和CIDW；OK的MAE低于PIDW，但最大偏差僅為0.007℃；AnisOK的MAE誤差為0.52，低于PIDW的0.54。由圖4(b)中可以看出：CIDW、FIDW和OK的RMSE隨著點數的增多而下降，在參考點數量為13以上時趨于穩定；OK的RMSE稍好于AIDW與KAIDW方法，但劣于CIDW和FIDW算法；AnisOK的RMSE誤差顯著低于CIDW、FIDW、OK、AIDW、KAIDW；PIDW的RMSE為0.78℃，比次優的AnisOK方法低0.02℃。圖4(c)中的MAX反映了與RMSE類似的規律：CIDW與FIDW插值算法隨著點數的增多穩步下降，其中FIDW的MAX略低于CIDW，而AIDW與KAIDW的MAX表現最差；OK的MAX總體上優于AIDW和KAIDW，但明顯差于CIDW和FIDW算法；PIDW的MAX顯著低于CIDW、FIDW、AIDW、KAIDW以及OK；AnisOK的MAX具備一定的優勢，相較于次優的PIDW方法，其最大值誤差還要低0.4℃。

圖4的結果表明：①顧及各向異的PIDW和AnisOK都顯著優于CIDW、FIDW、OK、AIDW和KAIDW算法；②不存在哪種插值算法，其MAE、RMSE與MAX的3個指標上都占據一致性的優勢；③顧及樣點分布均勻性的FIDW插值算法精度普遍優于CIDW；④采用一階鄰近點作為參考樣點的AIDW與KAIDW插值算法并未體現出較大的優勢，可能是由測試數據集中一些位于邊界區域的測試點所導致，顧及空間異質性的KAIDW未呈現比AIDW插值算法的優勢，可能是由于KAIDW對于局部空間異質性的分類存在較多的誤判；⑤OK相比于CIDW、FIDW、AIDW、KAIDW總體上并未呈現出明顯優勢，這可能是由于研究區域不能較好地滿足OK插值算法所需的平穩性假設條件，導致變異函數未能較好地反映氣溫變化的變異規律；⑥PIDW插值算法除在MAE指標稍劣于OK插值算法，在其余指標上相較于未顧及各向異性影響插值算法具備明顯的優勢；⑦除RMSE指標外，AnisOK在MAE和MAX指標上低于PIDW插值算法。

2.2 DEM插值

DEM插值數據來源于黃河山東濟南段大堤的1∶500大比例尺地形圖，共采集了639個高程點。黃河大堤為“梯形”構造，其中此段大堤南北方向起伏大，而東西向高程則變化平緩，其中平均高程為43.03 m，最大高程為49.30 m，位于大堤的頂部，最低高程36.31 m。

試驗中各算法的初始值與氣溫數據保持一致，PIDW算法得到最終的優化參數結果為[1.28，6，99，0]，各種算法的結果對比如圖5所示。

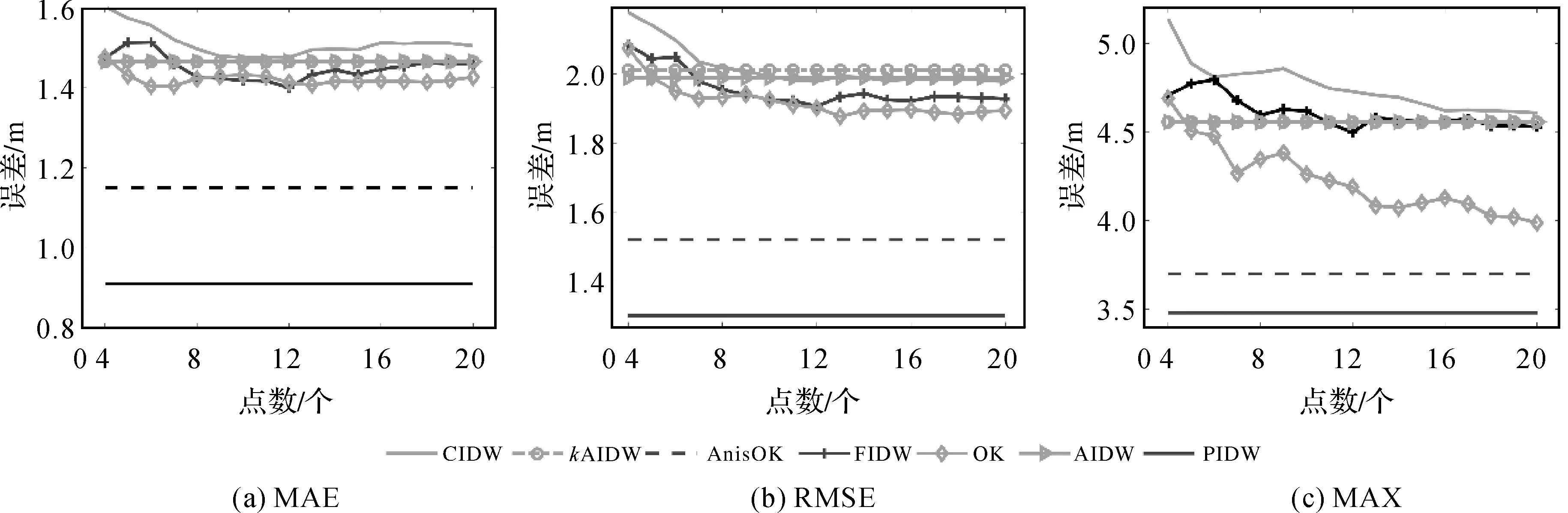
圖5 對比7種算法在DEM數據插值的MAE、RMSE和MAX結果Fig.5 Comparisons of seven different algorithms in DEM interpolation with MAE, RMSE and MAX measures

從圖5(a)中可以發現：隨著插值點數的增多，CIDW、FIDW與OK的MAE逐漸下降，在采樣點為12時達到最低，分別為1.43、1.37和1.42 m；AIDW與KAIDW的MAE低于CIDW算法，但大于其余3種算法；AnisOK的MAE誤差明顯低于CIDW、FIDW、OK、AIDW及KAIDW；PIDW表現出明顯的優勢，其MAE在7種插值算法中的誤差最小，比次優AnisOK的最小MAE值再少27.3 cm。圖5(b)中的RMSE表現出類似的結果：CIDW、FIDW和OK的RMSE隨著點數的增多呈現下降，在樣點為14以上時基本達到穩定狀態，并且OK的RMSE值最小；AIDW與KAIDW的RMSE的結果最差；AnisOK的RMSE低于除PIDW外的5種插值方法；PIDW的RMSE指標在所有算法中同樣呈現出明顯的優勢，比次優的AnisOK低27 cm左右。圖5(c)表明CIDW、FIDW與OK的MAX隨著點數增多而呈現下降趨勢，在參考點達到17以上基本保持穩定；AIDW和KAIDW比CIDW與FIDW能夠取得更優的效果，但PIDW的MAX顯著優于其他插值方法。總結以上兩個試驗結果，可得出以下結論：①顧及各向異性的AnisOK與PIDW幾乎在所有指標中都取得最小的誤差，表明在計算過程中顧及各向異性的空間屬性，將有助于提高模型的插值精度；②總體上PIDW的插值效果稍好于AnisOK方法，而且PIDW方法對數據無需假設前提，但地統計的AnisOK方法要求數據具有空間的二階平穩性。

2.3 參數分析

為了解釋PIDW插值算法有效性的原因，下面對模型的參數優化作進一步試驗分析。

2.3.1 各向異性對空間鄰近性的影響

由于各向異性能夠引起空間鄰近度的改變，因此設計對照試驗來分析各向異性對空間鄰近度的影響。圖6(a)和圖6(b)分別表示未顧及各向異性和顧及各向異性時對空間鄰近度的影響。由圖6(a)可知，當不顧及x或y方向的各向異性時，樣本點與參考點之間的距離為同心圓模式，而當顧及各向異性的影響時，“同心圓”距離模式被壓縮為“橢圓”，位于東西方向的樣本點具有更強的空間鄰近性。這表明PIDW的距離調節參數符合堤壩高程南北方向起伏大，而東西向變化平緩的事實。

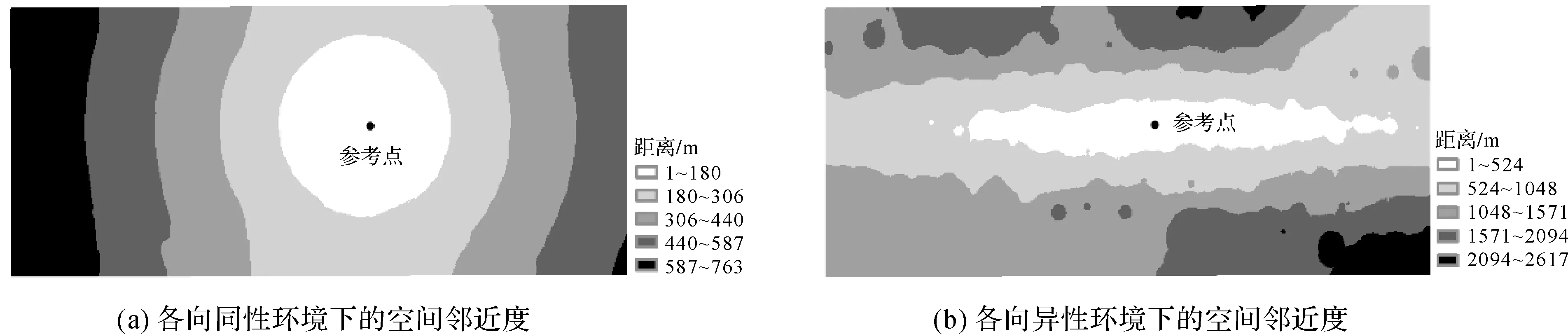
圖6 比較各向同性與各向異性環境下的空間鄰近度Fig.6 Comparisons the spatial proximity between isotropic and anisotropic measures

2.3.2 各向異性的方向對空間鄰近性的影響

考慮到各向異性的方向并不一定正好沿著坐標軸方向，而是存在一定的角度θ，本文設計一組對照試驗來分析各向異性的方向對空間鄰近性的影響。試驗2的原始數據高程在南北方向變化速率比東西方向大得多。為了體現各向異性方向不沿x或y軸時對空間鄰近性造成的影響，將試驗2的數據逆時針旋轉45°，即變換后的各向異性方向x_new與y_old之間的夾角約為135°(圖7)。

由圖7(a)可知，試驗1得到的參考點與其余各樣本點之間的距離基本為同心圓模式，不能真實地反映高程變化的空間鄰近性，同時試驗1得到的CV殘差和為2 894.4也再一次證明了其擬合精度較差。試驗2得到的CV殘差為1 400.4，其計算得到的各向異性方向與原始y軸間的夾角為132.66°(圖7(b))。可以發現，試驗2的CV殘差和較之于試驗1低很多，同時試驗2得到的各向異性方向與真實的方向相差僅為2.34°。同時由圖7(b)可知，正確反映各向異性的方向能夠得到準確的空間鄰近關系。

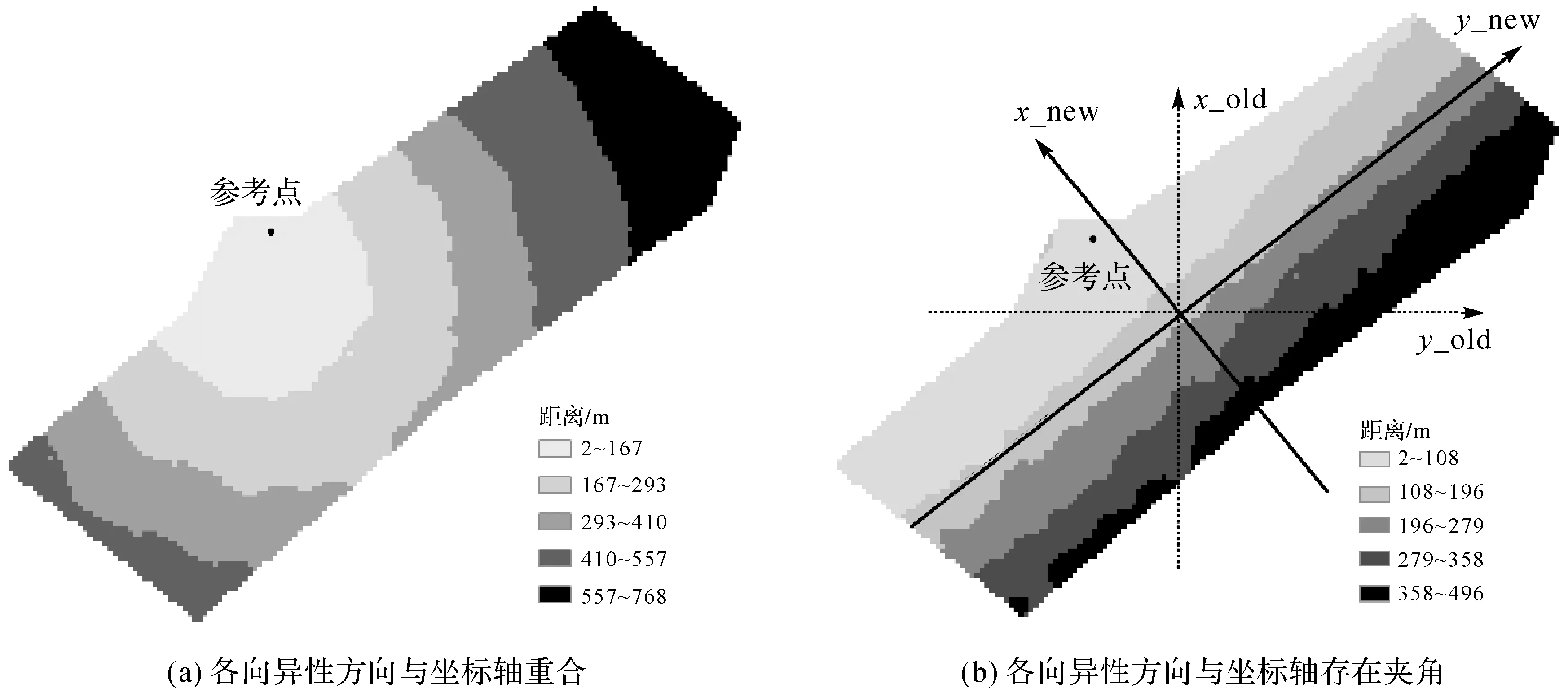
圖7 各向異性方向對空間鄰近度度量的影響Fig.7 Illustrations of the anisotropic effects on spatial proximity measurement

2.3.3 多參數優化對比分析

影響PIDW插值精度的參數主要有各向異性(距離調節參數λ與各向異性方向參數θ)，距離衰減系數α和最鄰近點數N。本文基于試驗1的數據，設計如下5個試驗來表明PIDW的插值精度由各參數共同決定，而單參數或少量參數的優化并不能取得插值的整體滿意效果：①固定距離調節參數為1，方向值為0，優化最鄰近點數與距離衰減系數；②固定距離衰減系數為2(ArcMap軟件默認值)，優化最鄰近點數、距離調節及各向異性方向參數；③固定最鄰近點數為12(ArcMap軟件默認值)，優化距離調節、各向異性方向參數及距離衰減系數；④固定方向值為0，同時優化距離衰減系數、最鄰近點數及距離調節參數；⑤距離衰減系數、最鄰近點數、距離調節與各向異性方向參數協同優化。試驗采用MAE、RMSE和CV殘差作為精度的評價指標，結果如圖8所示。

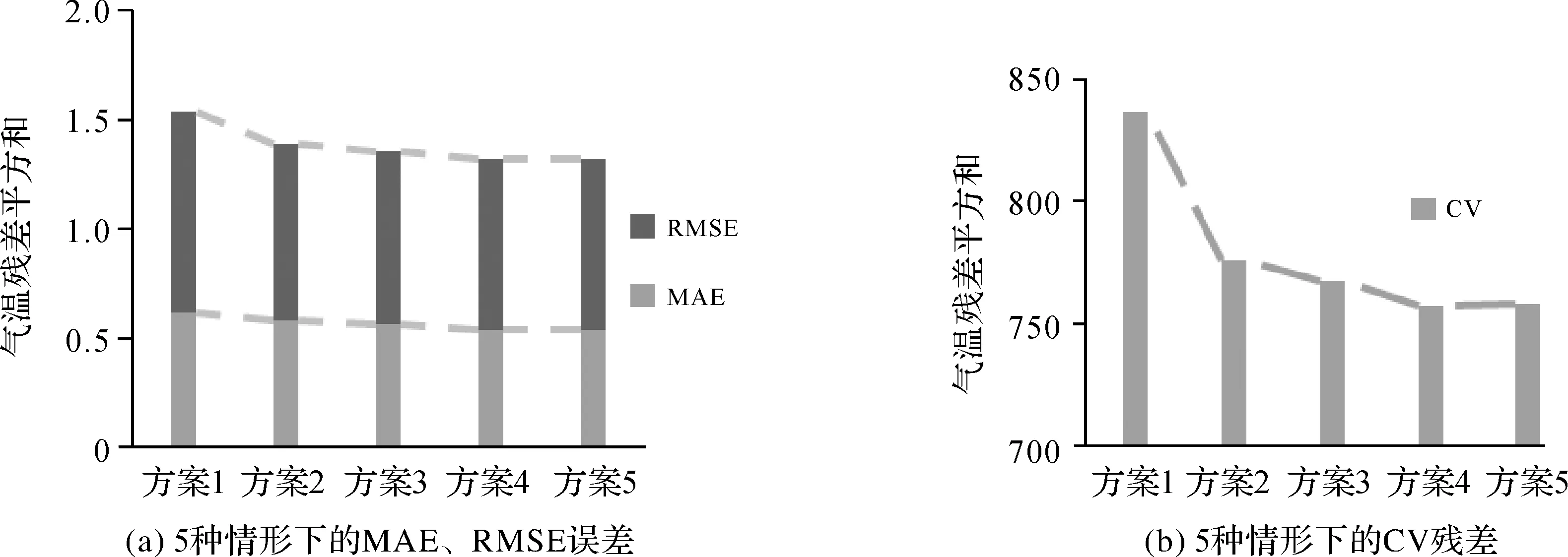
圖8 對比不同情形下參數優化的插值精度Fig.8 comparison the interpolating accuracies with optimized parameters for the different cases

從圖8可以看出方案1的效果最差，其MAE、RMSE以及訓練樣本的CV殘差值都最大。這是由于氣溫的分布存在較強的各向異性特征，如果插值過程中將距離調節參數固定為1，導致重要的參數不能正確地反映真實情況。方案2和方案3的MAE、RMSE和CV相較于方案1都有一定程度的提升，且方案3略優于方案2，表明本例中最鄰近點數對影響插值精度的重要性要低于距離衰減系數。方案4的CV殘差低于方案1、方案2和方案3，表明顧及各向異性影響能夠得到較好的插值效果。從圖8中還可以發現方案5的預測結果幾乎與方案4完全一致，僅有CV的殘差和相差0.1。這是由于氣溫變化沿著緯度方向變化速率較之于經度更快，而方案5優化的各向異性方向與方案4所固定的方向相同，因此其插值結果一致。由于粒子群算法的隨機性，導致它們的CV殘差和存在微小的差異。以上試驗表明如果僅優化部分參數均難以獲得插值效果的整體滿意解，采取多參數整體優化方法將有效增強模型插值精度。由于PIDW算法也可能存在過擬合的現象，導致預測精度的降低，因而在實際應用中需要注意避免PIDW算法的過擬合問題。

3 結 論

本文提出了顧及各向異性的多參數協同優化IDW插值算法PIDW，通過引入描述距離調節的參數λ以及角度的參數θ，將傳統的歐氏距離擴展為任意方向的“橢圓”距離，從而顧及各向異性對插值結果的影響；構造了基于CV檢驗的粒子群優化的適應度函數，將影響IDW插值精度的4個關鍵參數進行協同優化。利用不同尺度的空間數據驗證了PIDW算法的插值效果，結果表明顧及各向異性的AnisOK及PIDW能夠顯著提高各向異性環境下插值算法的精度，PIDW幾乎在所有指標中優于已有的IDW及OK插值方法。其次，PIDW總體插值效果稍好于AnisOK，并且不需要數據滿足二階平穩性假設條件，因此PIDW比AnisOK更具應用的普適性。

PIDW插值算法獲得的協同優化參數是一種全局意義下的滿意解。然而，當局部地理現象的變化特征與整體變化規律不一致時，那么PIDW算法得到的局部插值結果可能不如傳統的IDW插值方法；其次，由于采用粒子群算法對影響IDW插值精度的多個參數同步優化，處理效率比傳統IDW方法低。今后將在以下兩個方面開展研究：①利用GPU加速或并行處理技術提升PIDW插值算法的效率[27]；②研究能識別局部各向異性特征的LPIDW插值算法。