基于ABAQUS 的玄武巖-泥巖邊坡穩定性分析
張宇翀
(內蒙古工業大學,呼和浩特 010051)
0 引言
隨著21 世紀西部大開發,內蒙古地區加大了鐵路、公路等基礎設施的建設,所面臨滑坡造成的工程問題也急劇增加。對邊坡的安全穩定性進行研究分析,是滑坡工程問題進行防治減災的關鍵[1]。現代計算機技術的成熟,學者們多利用有限元分析法,確定邊坡的應力場和位移場,再利用強度折減法計算出邊坡的安全系數,并通過塑性區的發展表現出土坡失穩的過程[2]。邵龍潭[3-4]等人討論了邊坡穩定安全系數的物理意義,利用ABAQUS 有限元模擬軟件,通過強折減度法,分析彈性模量、容重、邊坡高度、坡面角、粘聚力以及內摩擦角的變化對安全系數的影響。王雷[5]采用室內模型試驗和數值模擬,研究分析降雨條件下黃土-基巖接觸面滑坡復活演化的過程及形成機理。但由于滑坡種類繁多,成因各異,使得研究復雜化。目前多是對黃土-泥巖接觸面滑坡進行研究,而對玄武巖-泥巖邊坡的安全穩定研究不足。
本文以內蒙古玄武巖-泥巖邊坡作為研究對象,通過三軸實驗研究不同含水率的泥巖的強度特性,為ABAQUS 有限元分析提供模型材料參數,通過強折減度法對玄武巖-泥巖邊坡進行穩定性分析,并研究影響玄武巖-泥巖邊坡穩定性的因素,為內蒙地區對玄武巖-泥巖邊坡的研究提供理論基礎。
1 泥巖強度特性實驗
1.1 試樣取樣及制備
試驗土樣取自內蒙古集寧區小紅山滑坡一側黏土出露處。土樣呈青灰色,較為堅硬。依據《土工試驗規程》(SL237-2019)對所取土樣進行三軸實驗。以土樣干密度為標準,配置含水率為16%、18%、20%、22%以及飽和的土樣,攪拌均勻后,密封放置在不通風并濕潤的環境靜置24小時,采用三瓣模成樣。試樣直徑38mm、高76mm。其中飽和試件采用兩步飽和法,即抽氣飽和法與反壓飽和法。在反壓飽和過程中,以30kPa的量級同時線性逐漸增加圍壓和反壓的方法,同時要始終保持圍壓比反壓大10~15kPa,當B值大于或等于0.95時,則認為試樣已達到飽和。
1.2 試驗方案及結果
三軸試驗儀器采用內蒙古工業大學GTX-100動三軸儀。對含水率為16%、18%、20%、22%及飽和的試件進行圍壓為50~150kpa的不固結不排水三軸試驗。圍壓為150kpa時,不同含水率條件下泥巖的三軸應力-應變關系分別如圖1所示,由圖可以看出泥巖應力應變曲線基本呈現硬化型,含水率對老黏土強度的影響很大。飽和試樣的峰值強度只有0.2Mpa,而16%的試樣其峰值強度可以達到1.0Mpa。
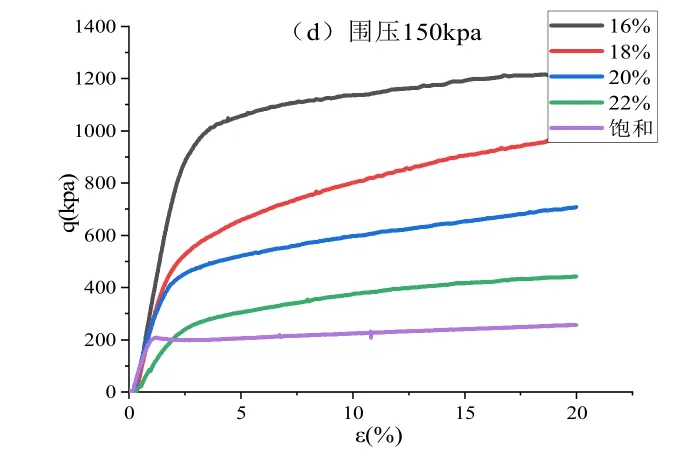
圖1 不同含水率在不同圍壓條件下的應力應變曲線
根據三軸試驗結果,得到了泥巖的強度指標如表1 所示。對表中泥巖不同含水率條件下抗剪強度參數進行數據分析,可以清晰的看出,粘聚力和內摩擦角總體上與含水率均呈現出負相關性。當含水率增加時粘聚力變化范圍較大,由154kpa 到48kpa 呈現指數型降低關系,降低了68%;而內摩擦角從41.65°到17.28°呈現線性降低關系,降低了58.5%,
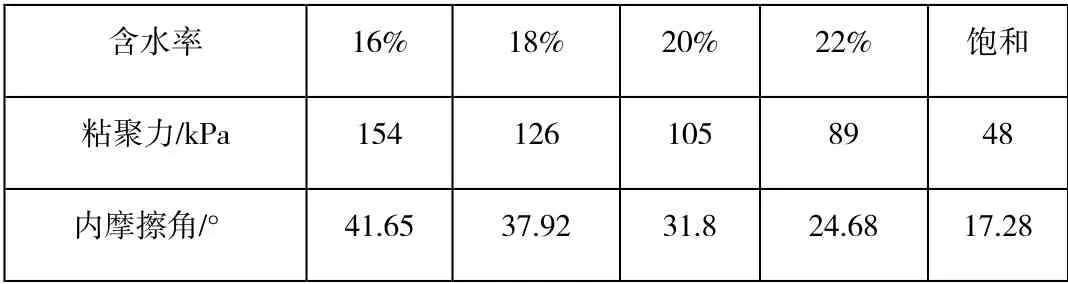
表1 不同含水率的泥巖強度參數
2 數值模擬
2.1 強度折減法
對于莫爾-庫倫材料,強度折減法安全系數表示為:

式中c 和是φ土體所能夠提供的抗剪強度;c′和φ′是維持邊坡平衡土體所需要的或實際提供的抗剪強度;Fv是強度折減系數。通過將邊坡原始粘聚力c 和內摩擦角φ同時除以折減系數Fv,不斷增大折減系數直至邊坡抗剪強度降低至達到臨界破壞狀態時,此時有限元模型折減系數的Fv大小即為邊坡的安全系數為Fs。
2.2 模型建立
選取集寧小紅山K17+410-K17+800 路段右側邊坡作為ABAQUS 計算模型,將邊坡簡化為玄武巖-泥巖的非均質邊坡,模型尺寸如圖2 所示。邊坡坡高60m,坡頂長30m,坡腳長10m,高10m,坡比為1:1.8,坡體覆蓋層玄武巖碎石土與下覆泥巖的結構面坡比為1:3。模型中的材料參數根據室內三軸實驗及國道335 線集寧至科布爾段公路工程地質勘查資料獲得,取天然含水率為20%時土體的粘聚力和內摩擦角作為模型參數,玄武巖碎石土容重為20.20kN/m3,彈性模量為50MPa,泊松比為0.25,粘聚力為32.8kPa,內摩擦角為14.2°;取泥巖容重為19.3kN/m3,彈性模量為10.94MPa,泊松比為0.35,粘聚力為105kPa,內摩擦角=31.8°。
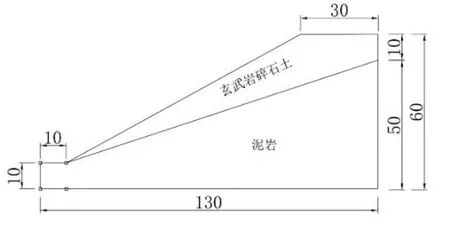
圖2 模型尺寸
建立計算模型,玄武巖碎石土與泥巖材料服從Mohr—Coulomb 破壞準則,限定模型兩側的水平位移和模型底部兩個方向的位移,采用4 節點的平面應變單元(CPE4),基于ABAQUS 模擬計算軟件采用平面應變有限元理論通過強度折減法對該邊坡進行穩定性分析。
2.3 計算結果
以折減系數F1=0.5 開始逐漸增加折減系數,在整個模型計算過程中不斷增加F1,將泥巖的強度參數c、ψ值通過強度折減系數F1進行折減,得到新的強度參數cr、ψr值,作為新強度參數進行計算。不斷增大折減系數直至邊坡抗剪強度降低至達到臨界破壞狀態時,此時有限元模型折減系數的F1大小即為邊坡的安全系數為Fs。
通過選取坡頂左側的頂點作為特征點,圖3 表示玄武巖-泥巖邊坡模型計算至不收斂過程中,特征點處折減系數F1與水平向位移的相互關系。當折減系數在0.5-1.62 區間內變化時,頂部特殊點水平位移無明顯變化,當折減系數在1.62-2.0 區間內變化時,邊坡頂點特殊點開始下滑,當折減系數為2.01時,頂點位移急劇增加。以特征部位的位移是否突變來作為評判邊坡是否失穩的標準,則對應位移拐點的安全系數為FS=2.01。
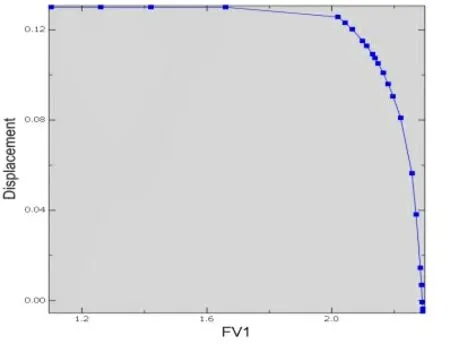
圖3 安全系數隨水平位移變化關系
為驗證 ABAQUS 有限元程序分析的可靠性,本文根據與ABAQUS 有限元軟件建立一致的邊坡模型參數,采用理正軟件分別按傳統計算方法——簡化Janbu法和簡化Bishop法進行計算。簡化Bishop法計算的安全系數為1.965,比有限元計算方法低2.2%,簡化Janbu 法計算的安全系數為1.957,低2.6%,與有限元方法計算出的結果一致,從而驗證了該模型的正確性。
3 泥巖的含水率對邊坡安全系數的影響
不同的泥巖含水率會使其的抗剪強度發生變化,為了考慮不同含水率的泥巖對玄武巖-泥巖邊坡穩定性的影響,取不同含水率的泥巖進行三軸實驗所得的抗剪強度數據(表1),改變有限元邊坡模型中泥巖的抗剪強度參數,模型尺寸及邊界條件均不變,分別設置模型泥巖含水率為16%、18%、20%、22%及飽和狀態時的強度參數,對其進行邊坡安全穩定分析,比較當泥巖為不同的含水率時玄武巖-泥巖邊坡的安全穩定系數的變化情況。
圖4 為不同泥巖含水率與安全系數的變化規律圖,由圖可知,泥巖的含水率在16%~飽和含水率范圍內變化時,泥巖的含水率與玄武巖-泥巖邊坡的安全系數呈反比關系。當含水率為16%時,安全系數為2.82,隨著泥巖含水率的增加,邊坡安全系數在降低,當含水率增加至飽和含水率時,安全系數為1.02。說明當含水率為飽和含水率時,玄武巖泥巖邊坡不穩定。
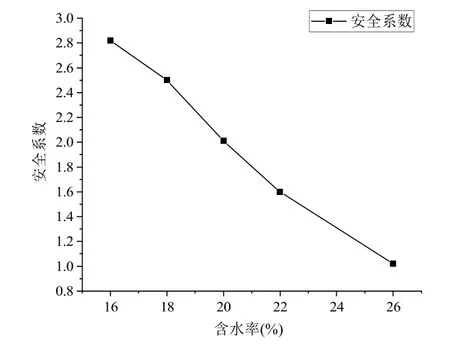
圖4 安全系數隨泥巖含水率的變化關系圖
4 結論
本文運用ABAQUS 有限元軟件對玄武巖—泥巖邊坡分析安全穩定性,并討論泥巖含水率的對其的影響,得到以下結論:
(1)隨著含水率的提高,相同圍壓條件下泥巖土樣破壞所需要的剪應力逐漸降低。
(2)玄武巖-泥巖邊坡隨著折減系數的增大,下覆泥巖層坡底處出現塑性區并向玄武巖碎石土層坡頂延伸形成滑動面,安全穩定系數為2.01。
(3)隨著泥巖含水率的增加,玄武巖-泥巖邊坡的安全系數在降低。當含水率為16%時,安全系數為2.82,含水率增加至飽和含水率時,安全系數為1.02,降低了64%。說明當含水率為飽和含水率時,玄武巖泥巖邊坡不穩定。

