基于支持向量機預測安達曼海南部內孤立波傳播特性

陸可瀟, 王 晶, 魏 鑫

基于支持向量機預測安達曼海南部內孤立波傳播特性

陸可瀟, 王 晶, 魏 鑫

(中國海洋大學 物理與光電工程學院, 山東 青島 266100)

內孤立波是發生在密度穩定層化海水中的一種特殊的海洋內波。預測內孤立波傳播難度較大。本文提出了一種方法, 利用美國麻省理工學院大氣環流模型(MITgcm)的內孤立波模型計算了大量模擬數據, 建立數據庫。采用機器學習的方法, 建立一個基于支持向量機(support vector machine, SVM)的安達曼海南部內孤立波傳播預測模型。最后運用安達曼海南部的Sentinel-1A合成孔徑雷達(SAR)圖像對內孤立波傳播預測模型結果進行檢驗。結果表明: 基于SVM的內孤立波傳播時間預測模型預測的時間平均絕對百分比誤差為8.43%, 平均絕對誤差為1.00 h。基于SVM的內孤立波到達位置預測模型預測的位置平均絕對百分比誤差為0.071%, 平均絕對誤差為0.069°。基于SVM的內孤立波振幅預測模型預測的振幅范圍為23.80～84.98 m。

內孤立波; MITgcm數值模擬; 支持向量機(SVM); 預測

海洋內波是發生在密度穩定層化的海水內部的一種波動, 其最大振幅出現在海洋內部[1]。內孤立波是一種具有大振幅、單向傳播、傳播速度快等特點的非線性內波[2]。內孤立波具有很強的垂向速度, 在海水營養物質的混合輸送中起著重要作用[3]。由于內孤立波在傳播過程中伴隨著巨大的擾動, 所以對海洋石油鉆井平臺和潛艇航行有很大的影響。因此, 內孤立波的預測工作具有重要的現實意義。印度洋的安達曼海幾十年來一直是研究內孤立波的經典區域。安達曼海的內孤立波最早是在油氣勘探中發現的。1975年底和1976年初, 美國埃克森石油公司在安達曼海南部實施了為期4個月的測量計劃和隨后的鉆井作業, 初步的測量確定了該區域存在大的內波, 觀測到的內波流速高達1.8 m/s。1976年10月, 在安達曼海南部的一個4 d測量計劃中也獲得了內波數據。Osborne等[4]根據現場觀測內波數據證實了內孤立波的存在。在安達曼海北部一名海員記錄的一次特殊事件中, 內孤立波通過時, 觀察到一個石油鉆井平臺傾斜了大約3°[5]。

人們對安達曼海的內孤立波進行了系統研究。Alpers等[6]利用SAR圖像研究了安達曼海內孤立波的生成位置與大陸架的相互作用。Hyder等[5]在安達曼海用實測的潮汐來預測內孤立波的發生。安達曼群島東北的內孤立波只出現在大潮中, 當潮差超過1.5 m時, 內孤立波發生的概率隨潮差的增大而增大。Jackson[7]利用中分辨率成像光譜儀(MODIS)觀測, 繪制了一張內孤立波的全球分布圖, 并證明內孤立波在安達曼海非常活躍。Da Silva等[8]利用SAR圖像研究了安達曼海的第一模態與第二模態內孤立波的潛在生成區域與機制。Shimizu等[9]使用高分辨率麻省理工學院通用環流模型MITgcm模擬和擴展Miles理論研究了安達曼海內孤立波斜相互作用。Sun等[10]利用MODIS影像給出了安達曼海內波的時空分布、產生源和傳播特征。Raju等[11]利用MODIS和SAR圖像來探測安達曼海內孤立波的潛在生成地點及其傳播特性。

綜上所述, 安達曼海內孤立波的研究大多集中在利用衛星圖像來觀測內孤立波的生成位置和時空分布, 而對于內孤立波的MITgcm數值模擬和預測研究非常少。安達曼海內孤立波多發, 可分為南部、中部和北部3個區域。因為這3個區域內孤立波大多數是由半日潮與海山相互作用產生, 機理相同, 因此只選南部為研究對象, 作為內孤立波傳播預測的示范區域。運用MITgcm模式來計算內孤立波的生成和傳播, 提取大量的內孤立波數據建立數據庫, 建立基于支持向量機(support vector machine, SVM)的安達曼海南部內孤立波傳播預測模型, 利用SAR圖像檢驗結果表明模型是有效的。

1 數據來源與數據庫建立

本文使用二維MITgcm模式來模擬安達曼海南部內孤立波的生成和傳播, 并從中提取數據建立數據庫。模擬海域選取在安達曼海南部(6.08°N, 94.6°E～97.1°E)。MITgcm采用非靜力近似模擬條件, 內部區域的水平網格分辨率為300 m(緯向), 垂直方向上的最大水深為1 448 m, 網格分為42層, 分辨率從5 m(海表面)至584 m(海底)依次遞增。為避免模式內生成的內孤立波及其他波動傳到邊界處發生反射, MITgcm采用海綿邊界條件[12]。將安達曼海的地形、溫度、鹽度和潮汐等數據輸入到MITgcm模式中, 地形數據取自ETOPO1 Global Relief Model (2009), 地形剖面圖如圖1所示。溫度和鹽度數據均來源于World Ocean Atlas(2013)的年平均數據, 潮汐數據來自美國俄勒岡大學開發的全球潮汐模式TPXO7.2的反演結果。

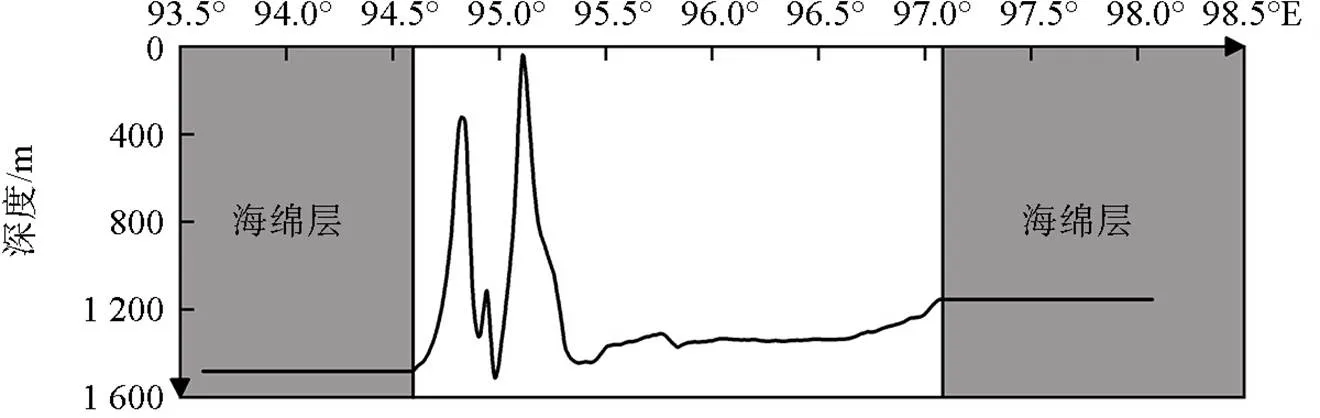
圖1 地形剖面圖

安達曼海內孤立波生成被廣泛認為是潮地相互作用機制。通過全球潮汐模式TPXO7.2獲得安達曼海13個分潮的速度緯向分量, 如表1所示。從表1中可以看出半日頻率的正壓潮在此地區占主導地位。因此采用4個半日潮(M2、S2、N2、K2)驅動MITgcm模型。把每天的潮汐速度作為初始強迫場輸入到MITgcm模型中, 得到每個潮汐下的內孤立波的產生和傳播過程。本文運用MITgcm模擬計算了潮汐速度0.05～0.1 m/s時的內孤立波生成與傳播, 提取了7 584條內孤立波的到達時間、位置和振幅。建立了潮汐速度振幅、經度、緯度、水深、時間和振幅6個參量建立數據庫, 把數據庫的數據進行隨機排序, 如表2所示。運用數據庫中不同的參量建立不同的模型, 來預測內孤立波的傳播時間、到達位置和振幅。

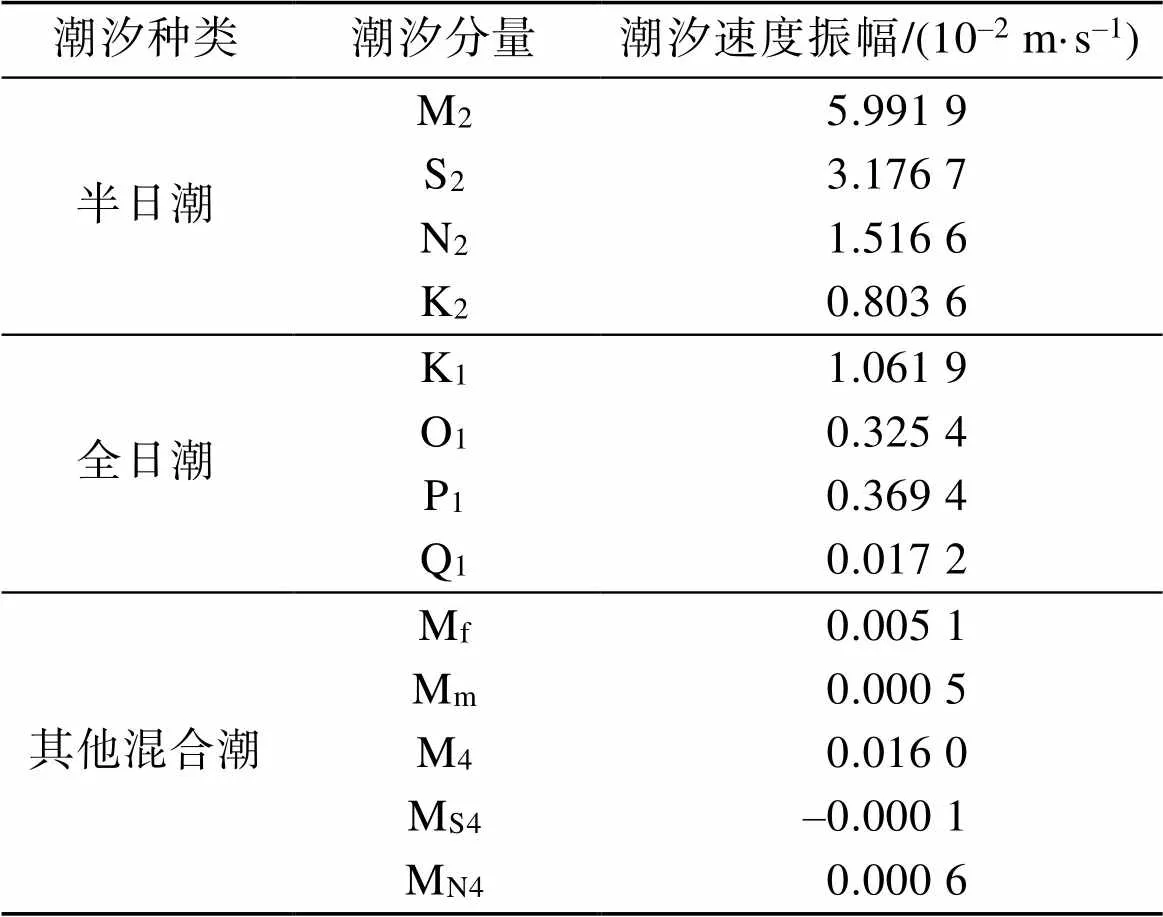
表1 TPXO7.2模型在(6.08°N, 94.6°E)反演得到13個潮汐緯向分量

表2 數據庫的模擬數據

續表

2 預測模型

運用支持向量機和大量的模擬數據建立安達曼海南部內孤立波傳播預測模型。通過模型來預測內孤立波的傳播過程, 包括傳播時間、位置和振幅。把數據庫中的7 584個模擬數據分為兩部分, 75%為訓練數據(序號1～5688), 25%為檢驗數據(序號5689～7584)。為衡量模型預測的性能, 采用相關系數(correlation coefficient), 平均絕對誤差AE(mean absolute error)和平均絕對百分比誤差APE(mean absolute percentage error)作為模型的評價指標。上述評價指標值越大,AE和APE值越小, 則預測效果越好。其表達式如下:

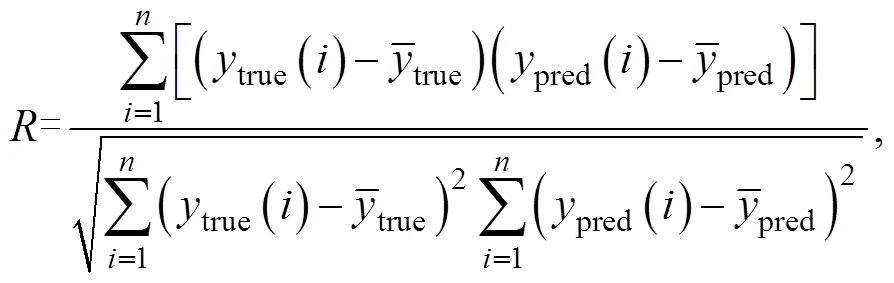
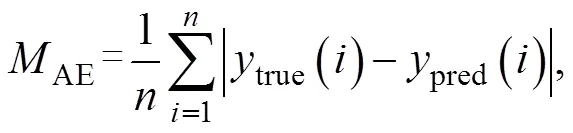
式中:為預測個數,true為真實值,pred為模型預測值。

支持向量機(support vector machine, 簡稱SVM)由Cortes和Vapnik于1995年正式提出[13]。它是一種基于統計學習理論的有監督機器學習方法, 被廣泛地運用在模式識別、函數擬合和時間序列估計等領域, 進行數據分類[14]、回歸和預測[15-16]研究。本文采用的SVM參數有: SVM設置類型(-), 核函數(-), 懲罰系數(-), 核函數中的gamma函數(-), epsilon-SVR中的損失函數(-)。

2.1 內孤立波時間預測模型

把內孤立波到達位置的經度、水深和潮速振幅3個參量作為模型輸入參量, 內孤立波到達時間作為模型輸出。內孤立波時間預測模型確定SVM設置類型-4, nu-SVR是支持向量回歸機, 由于epsilon-SVR需要事先確定參數, 然而在某些情況下選擇合適的參數卻不是一件容易的事情, 而nu-SVR能夠自動計算參數。經過多次試驗和對比驗證, 確定核函數設置類型-0, 線性核函數主要用于線性可分的情形。參數少, 速度快, 對于一般數據, 預測效果比較理想。

對時間預測模型檢驗結果繪制成時間數據散點圖和偏差概率圖, 并計算散點圖的相關系數、平均絕對百分比誤差及平均絕對誤差, 如圖2所示。通過兩者比較可以得知基于SVM的內孤立波時間預測模型的APE為1.17%,AE為0.22 h。從圖2中可以看出數據點在散點圖中分布比較集中,為0.999 5, 相關度較高。時間數據偏差在0 h附近的數據出現概率最高, 主要集中在–0.4 h到0.4 h之間, 出現概率為0.893, 預測效果較理想。

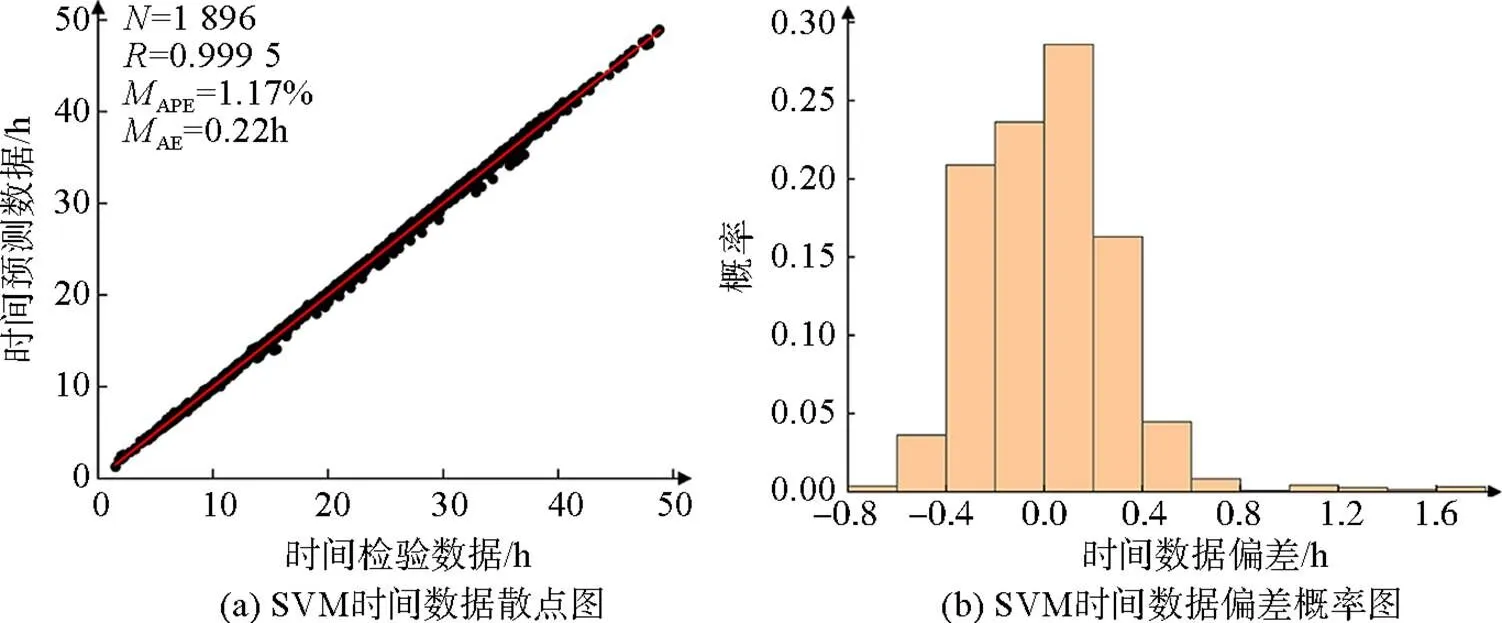
圖2 SVM時間數據散點圖和偏差概率圖

2.2 內孤立波位置預測模型

把時間、水深和潮速振幅3個參量作為模型輸入, 到達位置的經度作為模型輸出。內孤立波位置預測模型和時間預測模型的設置是一樣的, SVM設置類型-4, 核函數設置類型-0。經過多次試驗和對比驗證, 這個設置不僅適合于時間預測, 也同樣適合于到達位置預測。模型檢驗結果的時間數據散點圖和偏差概率圖如圖3所示。通過兩者對比可以得出基于SVM的內孤立波位置預測模型的APE為0.016%,AE為0.015°。從圖3中可以看出雖然有個別數據點分散, 但是大部分數據點在散點圖中分布較為集中, 相關系數為0.999 1, 相關度較高。經度數據偏差在–0.01°附近的數據出現概率最高, 主要集中在–0.02°到0.03°之間, 出現概率為0.865, 預測結果比較好。

圖3 SVM經度數據散點圖和偏差概率圖

2.3 內孤立波振幅預測模型

把時間、經度、水深和潮速振幅4個參量作為模型輸入, 振幅作為模型輸出。內孤立波振幅預測模型確定SVM設置類型-3, epsilon-SVR對應不敏感損失函數的支持向量回歸機, 對樣本點來說, 存在著一個不為目標函數提供任何損失值的區域。經過多次試驗和對比驗證, 確定epsilon-SVR中的損失函數=0.05, 核函數設置類型-2, RBF核函數因為其追蹤性能好且無記憶性, 通過調節核參數更能反映訓練數據的范圍分布, 預測效果較好。通過多次參數尋優得到懲罰系數best=0.031 25, RBF核函數中的gamma函數best=8。

檢驗模型結果見繪制時間數據散點圖和偏差概率圖, 并計算散點圖的相關系數、平均絕對百分比誤差及平均絕對誤差, 如圖4所示。通過計算得出基于SVM的內孤立波振幅預測模型的APE為10.00%,AE為3.88 m。從圖4中可以看出數據點在散點圖中分布有點分散, 但是整體上是較為集中的,=0.975 8, 相關度較高。數據偏差在0 m附近的數據出現概率最高, 數據偏差比較分散, 主要集中在–8 m到8 m之間, 出現概率為0.886, 預測結果是可以接受的。

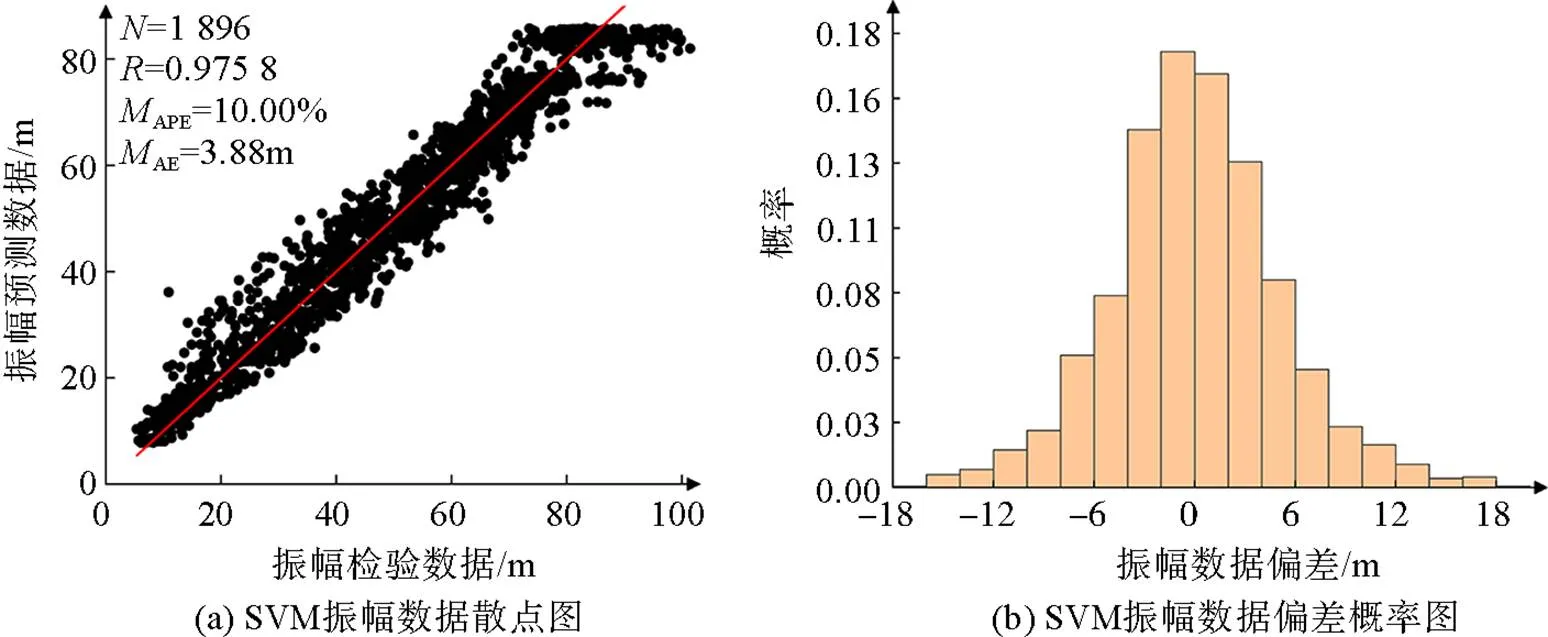
圖4 SVM振幅預測數據散點圖和偏差概率圖

3 模型經度驗證

在安達海南部海域(5°N～7°N, 94°E～100°E), 收集了2018全年的Sentinel-1A SAR圖像。在所有的圖像中總共篩選出3景匹配的圖像, 如圖5所示。

從3景圖像中選擇5條明顯的內孤立波, 確定其位置后, 通過ETOPO1獲得紅點位置的水深, 通過TPXO7.2獲得內孤立波生成源處的潮速振幅, 如表3所示。運用SVM把7 854個模擬數據作為訓練集進行模型訓練, 然后運用訓練好的模型來預測圖像中的傳播時間、位置和振幅, 最終把預測數據與SAR圖像數據做對比。

圖5 安達曼海南部Sentinel-1A SAR圖像

注: 圖中數字與表3中數字相對應, 圖中紅點為表3數據的提取位置。

表3 SAR圖像數據

3.1 內孤立波到達時間預測

把經度、水深和潮速振幅3個參量作為模型輸入, 時間作為模型輸出。通過SVM的內孤立波時間預測模型, 得到時間預測數據, 如表4所示。圖6是SVM預測的時間數據和圖像時間數據對比圖。圓形代表通過SVM時間預測模型預測的時間數據, 正方形代表SAR圖像的時間數據。通過比較可得, SVM模型預測的時間數據和SAR圖像時間數據的APE為8.43%,AE為1.00 h。

表4 SVM時間預測結果

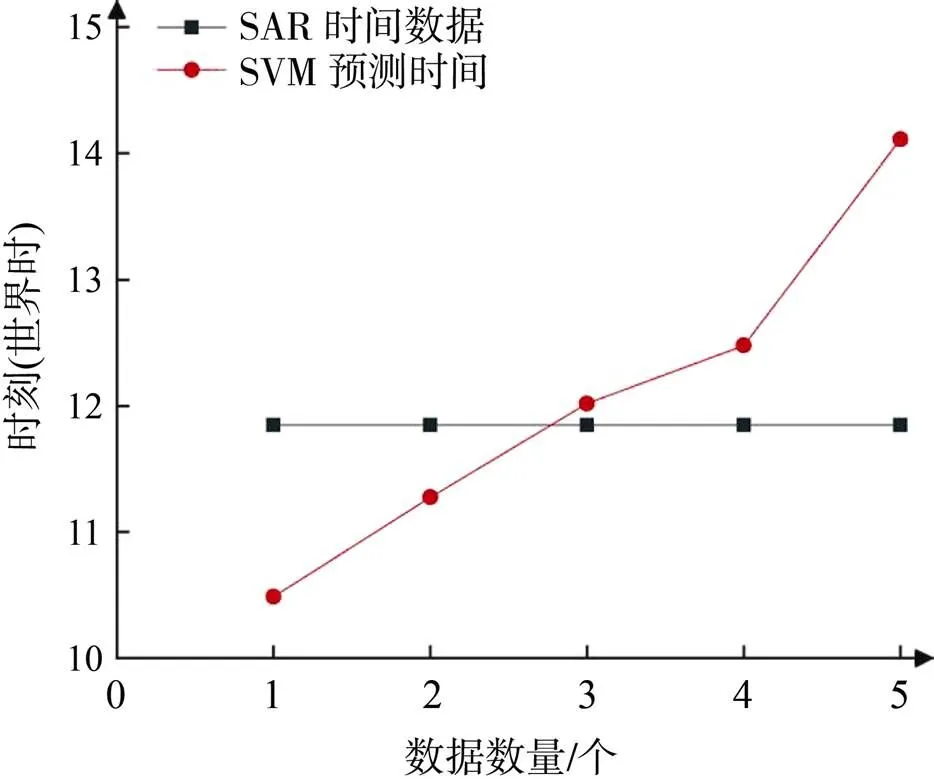
圖6 SVM預測時間數據和SAR圖像時間數據對比圖

3.2 內孤立波位置預測模型結果

本文把時間、水深和潮速振幅3個參量作為模型輸入, 經度作為模型輸出。表5顯示了基于SVM的內孤立波位置預測模型的經度預測數據和SAR圖像經度數據。經度預測數據和圖像經度數據對比圖如圖7所示。從圖7可以得出, 圓形代表通過SVM模型得到的預測經度數據, 正方形代表SAR圖像經度數據。通過對比得知, SVM模型預測經度和SAR圖像經度的APE為0.072%,AE為0.069°。圖7中的兩條曲線擬合程度較好, 預測結果較理想。

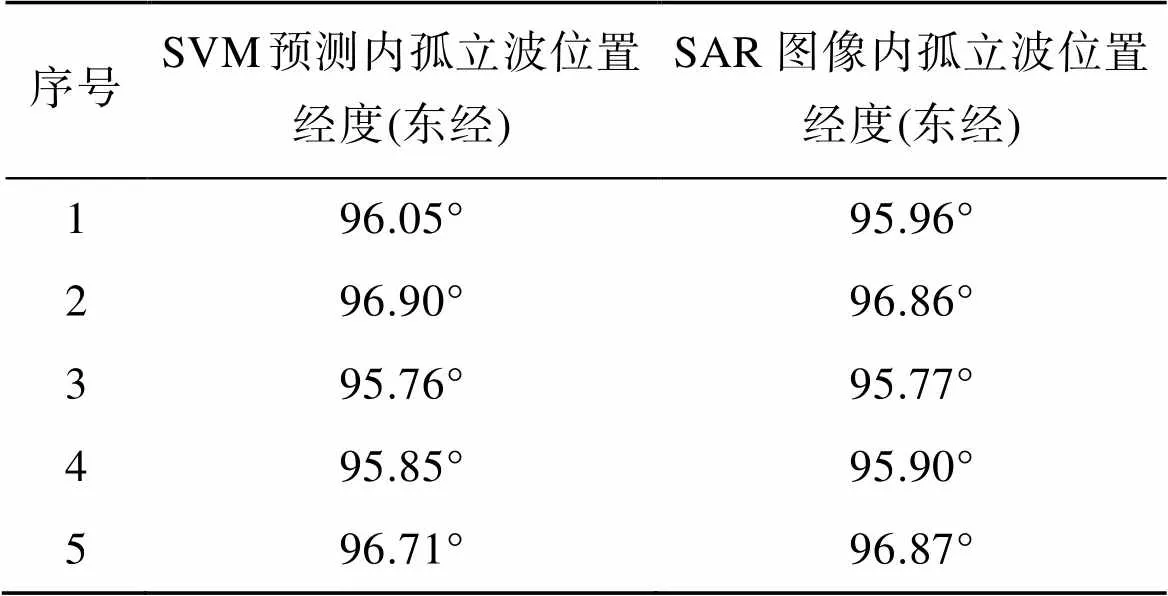
表5 SVM經度預測結果

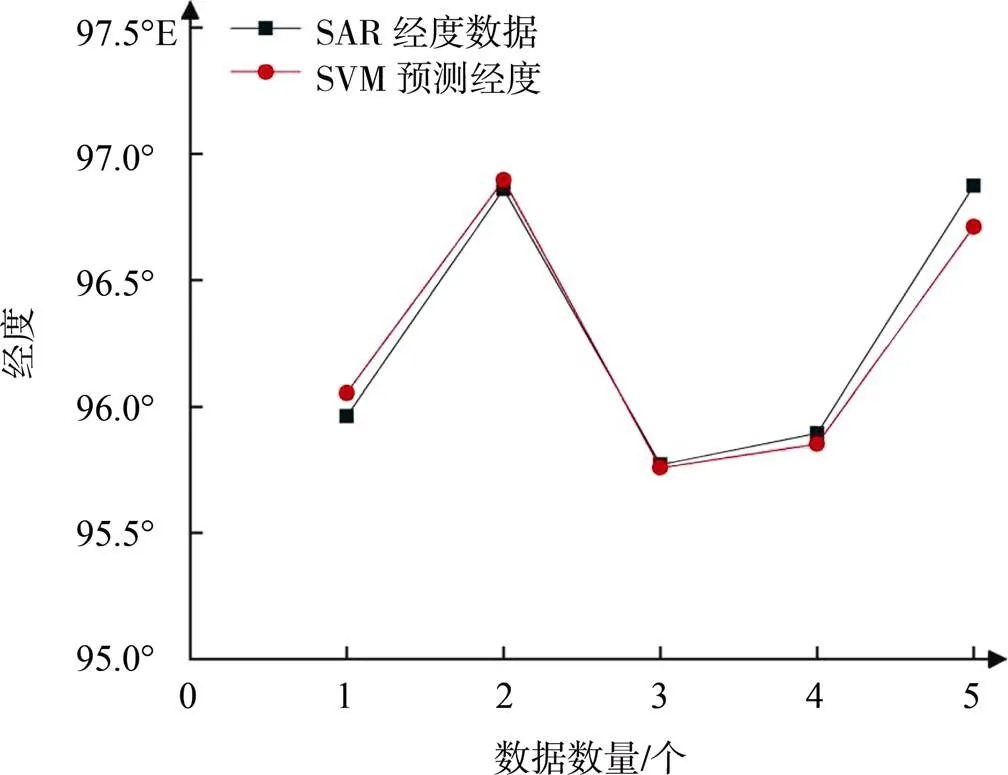
圖7 SVM預測經度數據和圖像經度數據對比圖

3.3 內孤立波振幅預測模型結果

把時間、經度、水深和潮速振幅4個參量作為模型輸入, 振幅作為模型輸出。通過SVM的內孤立波振幅預測模型, 得到振幅預測數據, 如表5所示。SVM振幅預測數據的最大振幅為84.98 m, 最小振幅為23.80 m, 平均振幅為56.26 m。從表6中可以看出, SVM振幅預測數據的最大值在農歷二月初五。這一天的潮汐速度最大, 并且內孤立波經度也最大。SVM振幅預測數據的最小值在農歷四月初六。這一天的潮汐速度較小, 而且內孤立波經度最小。由于沒有與遙感數據相匹配的現場實測數據, 所以將SVM振幅預測的結果與歷史的實測數據進行對比。Osborne等[4]在安達曼海南部1 093 m深的水域, (6°53′N, 97°04′E)位置處測量到振幅為60 m的內孤立波。實測位置和預測位置接近, 預測的平均振幅和實測振幅差距較小, 所以內孤立波振幅預測結果是合理的。

表6 SVM振幅預測結果

4 結論

本文提出了一種基于機器學習來預測內孤立波傳播的新思路, 并建立了基于SVM的安達曼海南部內孤立波傳播預測模型。首先運用全球潮汐模式TPXO7.2得到潮汐速度, 以潮汐速度為初始強迫場構造出不同潮汐速度下的MITgcm模式的內孤立波數值計算模型。通過MITgcm模擬計算了潮汐速度0.05～ 0.1 m/s的內孤立波生成與傳播過程, 總共提取了7 584條內孤立波。然后把7 584個模擬數據分為兩部分, 5 688個數據為訓練數據, 1 896個數據為檢驗數據。采用SVM方法建立了安達曼海南部內孤立波傳播預測模型。在模型建立的過程中, 基于SVM的內孤立波傳播預測模型的時間模型的為0.999 5,APE為1.17%,AE為0.22 h。位置模型的為0.999 1,APE為0.016%,AE為0.015°。振幅模型的為0.975 8,APE為10.00%,AE為3.88 m。

然后運用Sentinel-1A的SAR圖像中的數據來驗證模型的準確性。通過與SAR圖像對比可得, SVM模型預測的時間數據和圖像時間數據的APE為8.43%,AE為1.00 h。SVM模型預測的經度和圖像經度的APE為0.072%,AE為0.069°。SVM的振幅預測數據平均振幅為56.26 m, 歷史上的實測數據振幅為60 m, 兩者比較接近。因此, SVM的安達曼海南部內孤立波傳播預測模型是有效的, 可為石油勘探和海洋決策部門預警提供參考。

[1] 方欣華, 杜濤. 海洋內波基礎和中國海內波[M]. 青島: 中國海洋大學出版社, 2005: 1-4.

FANG Xinhua, DU Tao. Fundamentals of oceanic internal waves and internal waves in the China seas[M]. Qingdao: China Ocean University Press, 2005: 1-4.

[2] 段亞男. 基于ARM嵌入式技術監測海洋內孤立波傳播特征的系統設計[D]. 青島: 青島理工大學, 2013.

DUAN Ya’nan. Designing based on ARM embedded technology to detect propagation characteristics of internal solitary waves[D]. Qingdao: Qingdao University of Technology, 2013.

[3] 藺飛龍. 南海北部內波特征研究及機理分析[D]. 北京: 中國科學院大學, 2014.

LIN Feilong. Characteristics and mechanism analysis of internal waves in the northern South China Sea[D]. Beijing: University of Chinese Academy of Sciences, 2014.

[4] OSBORNE A R, BURCH T L. Internal solitons in the Andaman sea[J]. Science, 1980, 208(4443): 451-460.

[5] HYDER P, JEANS D R G, CAUQUIL E, et al. Observations and predictability of internal solitons in the northern Andaman Sea[J]. Applied Ocean Research, 2005, 27(1): 1-11.

[6] ALPERS W, HENG Wangchen, LIM Hock. Observation of internal waves in the Andaman Sea by ERS SAR[J]. European Space Agency, (Special Publication) ESA SP, 1997, 414(3): 1287-1291.

[7] JACKSON C. Internal wave detection using the moderate resolution imaging spectroradiometer (MODIS)[J]. Journal of Geophysical Research: Oceans, 2007, 112: C11012.

[8] DA SILVA J C B, MAGALHAES J M. Internal solitons in the Andaman Sea: a new look at an old problem[C]// Proceedings of the Remote Sensing of the Ocean, Sea Ice, Coastal Waters, and Large Water Regions. Edinburgh, UK: SPIE Remote Sensing, 2016, 9999(999907).

[9] SHIMIZU K, NAKAYAMA K. Effects of topography and earth’s rotation on the oblique interaction of internal solitary-like waves in the Andaman Sea[J]. Journal of Geophysical Research: Oceans, 2017, 122(9): 7449-7465.

[10] SUN Lina, ZHANG Jie, MENG Junmin. A study of the spatial-temporal distribution and propagation characteristics of internal waves in the Andaman Sea using MODIS[J]. Acta Oceanologica Sinica, 2019, 38(7): 121-128.

[11] RAJU N J, DASH M K, DEY S P, et al. Potential generation sites of internal solitary waves and their propagation characteristics in the Andaman Sea-a study based on MODIS true-colour and SAR observations.[J]. Environmental monitoring and assessment, 2019, 191(Suppl 3): 809.

[12] ZHANG Z, FRINGER O B, RAMP S R. Three-dimen-sional, nonhydrostatic numerical simulation of nonlinear internal wave generation and propagation in the South China Sea[J]. Journal of Geophysical Research Oceans, 2011, 116(C5): C05022.

[13] CORTES C, VAPNIK V N. Support-Vector networks[J]. Machine Learning, 1995, 20(3): 273-297.

[14] 張錦水, 何春陽, 潘耀忠, 等. 基于SVM的多源信息復合的高空間分辨率遙感數據分類研究[J]. 遙感學報, 2006, 10(1): 49-57.

ZHANG Jinshui, HE Chunyang, PAN Yaozhong, et al. The high spatial resolution RS image classification based on SVM method with the multi-source data[J]. Journal of Remote Sensing, 2006, 10(1): 49-57.

[15] 吳恒, 余秋鵬. 基于SVM預測電動汽車并網局部電壓穩定的研究[J]. 電工電氣, 2019(10): 9-13.

WU Heng, YU Qiupeng. Research on prediction of local voltage stability of electric vehicles based on SVM[J]. Electrotechnics Electric, 2019(10): 9-13.

[16] 徐娟, 卞良. 基于SVM的中文垃圾郵件預測系統研究[J]. 數字技術與應用, 2020, 38(355): 48-49.

XU Juan, BIAN Liang. Research on Chinese spam prediction system based on SVM[J]. Digital Technology and Application, 2020, 38(355): 48-49.

The prediction of internal solitary wave propagation characteristics in the southern Andaman Sea based on a support vector machine

LU Ke-xiao, WANG Jing, WEI Xin

(College of Physics and Optoelectronic Engineering, Ocean University of China, Qingdao 266100, China)

Internal solitary wave (ISW) is a special type of internal wave. It occurs in density-stable stratified seawater and have strong randomness. Their occurrence location, arrival time, amplitude, and other parameters are greatly affected by hydrology and other aspects of the external environment. Therefore, accurate prediction of internal solitary waves propagation is a recognized challenge. In this paper, a method is proposed to use the Massachusetts Institute of Technology general circulation model (MITgcm) of ISWs to calculate abundant simulation data and establish a database. A prediction model of ISWs propagation in the southern Andaman Sea based on a support vector machine (SVM) is established using machine learning. Finally, the Sentinel-1 synthetic aperture radar (SAR) images in the southern Andaman Sea are used to test the results of the ISWs propagation prediction model. The results demonstrate that the mean absolute percentage error of time (location) predicted by the prediction model of ISWs propagation time (arrival location) based on an SVM is 8.43% (0.072%), and the mean absolute error is 1.00 h (0.069°). The predicted amplitude range of the ISWs amplitude prediction model based on an SVM is 23.80～84.98 m.

internal solitary waves; MITgcm numerical simulation; support vector machine(SVM); prediction

Nov. 5, 2020

TP79

A

1000-3096(2021)05-0031-08

10.11759/hykx20201105007

2020-11-05;

2021-01-07

國家重點研發項目(2017YFC1405600)；國家自然科學基金項目(61871353)

[National Key R&D Program of China, No. 2017YFC1405600; Natural Science Foundation of China, No. 61871353]

陸可瀟(1995—)，男，山東青島人，碩士研究生，研究方向：海洋遙感，E-mail：lukexiao1234@163.com；王晶（1962—），通信作者，教授，博士生導師，主要從事光纖光學和海洋遙感研究，E-mail：wjing@ouc.edu.cn

(本文編輯: 叢培秀)